Ask Ethan: What would an antimatter black hole teach us?

All throughout the Universe, one theme resonates no matter where we go. Whether in the depths of intergalactic space, the plasma-rich region surrounding galaxies and galaxy clusters, or the dense confines of star clusters, stars, or even planetary systems, everything we see is definitively made up of matter and not antimatter. Somehow, although the mechanism has yet to be determined, the Universe isn’t symmetric. Rather, matter won out over antimatter from very early times, and all of the structures we can access, within the visible Universe, are made from matter, not antimatter.

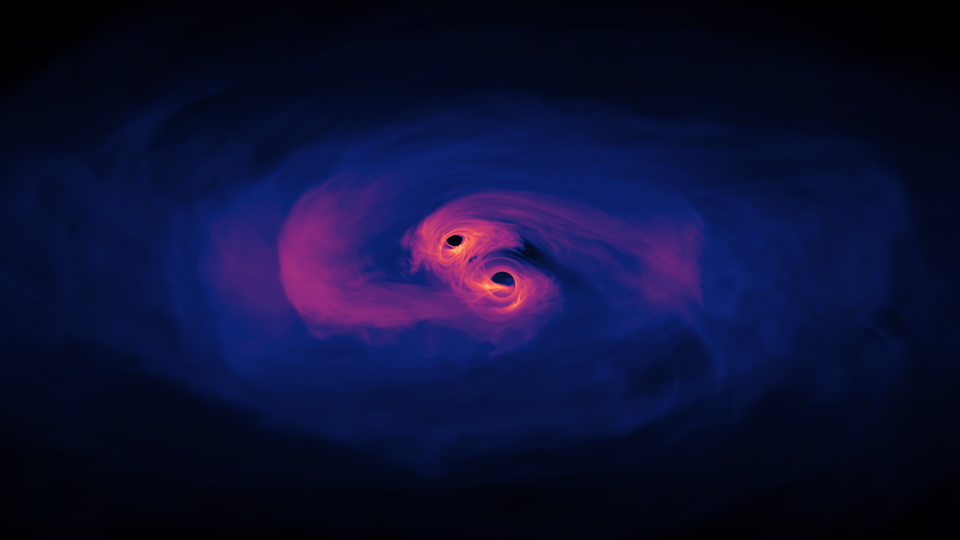
Black holes can only arise from material that collapses, which means all of the black holes in our Universe must have been made from matter, not antimatter. But what if there were an antimatter black hole? Would there be anything different about it? What about when an antimatter black hole merged with a matter-based one? That’s the question from Jim Chappell, who wants to know:

“What do you think would happen differently, if anything, if a black hole composed of anti-matter coalesced with one made of matter? [Would there be any] detectable/observable difference in the result?”

The answer, perhaps surprisingly, depends on how closely you’re able to look.

When two black holes inspiral and merge, a significant portion of their mass can get converted into energy in one very short time interval. The gravitational radiation that these black holes emit doesn’t propagate across the Universe instantaneously, but rather is limited by the finite speed of propagation: the speed of light.

According to Einstein’s General Relativity, black holes don’t particularly care what they are made out of. If you put a sufficient amount of mass together in a small enough volume of space, the gravitational pull within that region will prevent anything below a certain speed from escaping. Dial up the amount of mass, and it becomes harder and harder to escape; you’ll have to move even faster in order to do so. And for better or worse there’s a limit to how quickly anything can move within our Universe: the speed of light in a vacuum.

Whenever the speed needed to escape a region’s gravitational pull is greater than the speed of light, that’s the necessary condition for creating a black hole. In fact, the event horizon is defined by the border from where you can versus where you can’t escape. In one of the more famous theorems in General Relativity, there are only a few types of properties that a black hole can remember. They include:

• mass,
• electric charge,
• angular momentum,
• and, if it was to exist, magnetic charge,

and these properties are known as the types of “hair” a black hole can have. Although the shape and specific properties of a black hole’s interior are defined by the values of these types of hair, there’s no distinction between whatever other properties went into the composition of a black hole.

One of the most important contributions of Roger Penrose to black hole physics is the demonstration of how a realistic object in our Universe, such as a star (or any collection of matter), can form an event horizon and how all the matter bound to it will inevitably encounter the central singularity. Once an event horizon forms, the development of a central singularity is not only inevitable, it’s extremely rapid.

In other words, if you had a black hole that was made out of 100% neutrons versus an otherwise identical one that was made out of 100% anti-neutrons, those two black holes would each have the same mass, the same charge, and the same angular momentum as one another. We know, from both a tremendous variety of particle physics experiments and also a variety of provable theorems — such as the CPT theorem — that every fundamental and composite particle that’s made out of matter has an antimatter counterpart: of equal mass, equal-and-opposite angular momentum, and equal-and-opposite electric charge.

It’s also true, however, that if you collide a matter particle with its antimatter counterpart, they annihilate away back to pure energy via Einstein’s E = mc², with the mass of the matter particle and the antimatter (anti)particle both being equal. You might think, therefore, that colliding a matter-composed black hole with an antimatter-composed black hole would cause the two to annihilate away, releasing a tremendous amount of energy in the process, but this shouldn’t be the case. Once you create a black hole, it no longer “remembers,” at least, in General Relativity, what it was that it was made out of.

In the vicinity of a black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. Unlike in the non-rotating case, the event horizon splits into two, while the central singularity gets stretched out into a one-dimensional ring. Nobody knows what occurs at the central singularity, but it only must exist if all possible paths inevitably lead to it. This is true in the non-rotating case, but is it true in the rotating case?

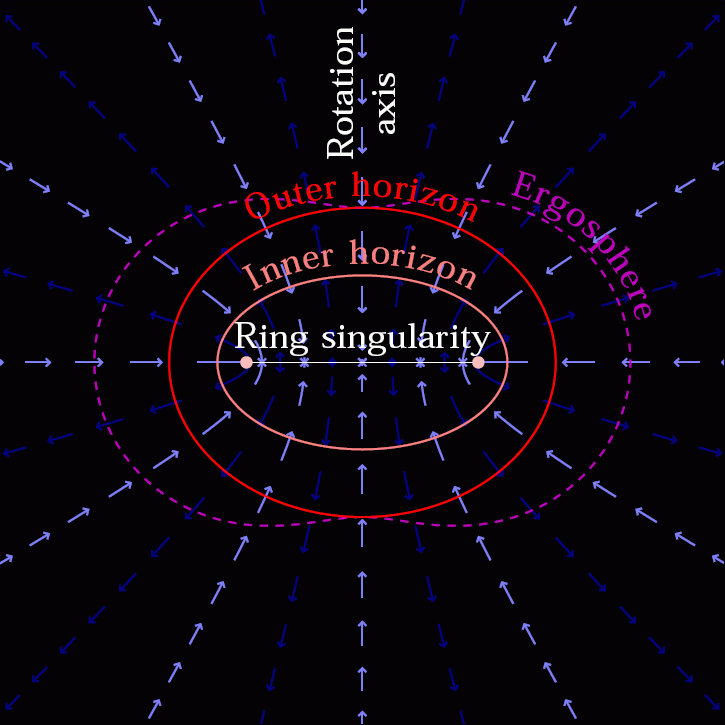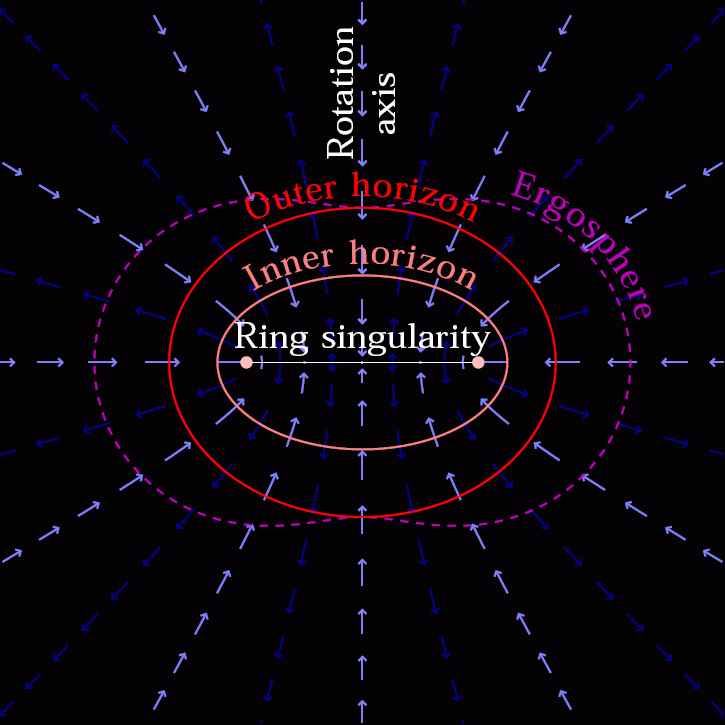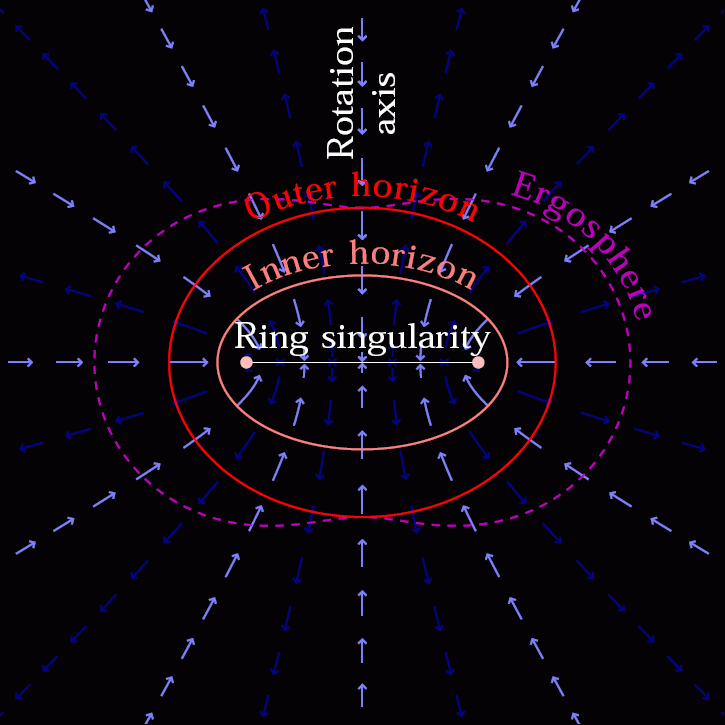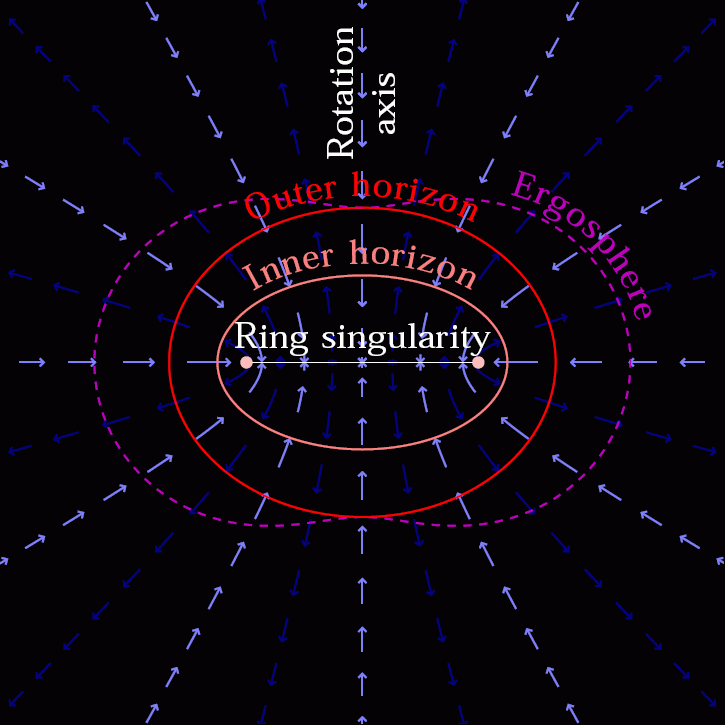
We fully expect that black holes, like anything with mass, will gravitate according to the laws and rules set forth by our theory of gravitation: General Relativity. Since antimatter and matter have equal amounts of mass, that means a black hole made out of antimatter, when paired with a black hole made out of matter, should orbit, emit gravitational waves, inspiral, and eventually merge in the same exact fashion that two black holes made of normal matter should.

An antimatter black hole should have:

• the same size-and-shape event horizon,
• the same rest mass,
• the same gravitational influence on the surrounding matter-and-antimatter,
• the same emission of gravitational waves,
• the same inspiral-and-merger period,
• the same precessions,
• the same angular momentums,
• the same post-merger kicks,
• and even the same spectrum and rates of Hawking radiation

as a normal matter black hole is expected to have. When they do merge with another (whether matter or antimatter) black hole, the same proportion of mass — about 10% of the lower-mass object in the merger — should get emitted in the form of gravitational radiation.

A mathematical simulation of the warped space-time near two merging neutron stars that result in the creation of a black hole. The colored bands are gravitational-wave peaks and troughs, with the colors getting brighter as the wave amplitude increases. The strongest waves, carrying the greatest amount of energy, come just before and during the merger event itself. What occurs outside the event horizon is not practically affected by whether there is a ring singularity at the center, or some other, extended object that is non-singular.

But, with that said, General Relativity isn’t everything. There are also quantum rules that govern the Universe, and some of those rules show stark differences between different types of matter, as well as between matter and antimatter. For example, if you make a black hole out of:

• a solar mass’s worth of protons-and-electrons,
• a solar mass’s worth of neutrons,
• a solar mass’s worth of positrons-and-antiprotons,
• or a solar mass’s worth of antineutrons,

these black holes should not be the same.

From the viewpoint of General Relativity, they would be considered identical. They have the same mass as one another: one solar mass. They have the same electric (and, for that matter, magnetic) charge: a net of zero. And they should have identical spins/angular momenta to one another, dependent only on their formation history.

But from a quantum viewpoint, they ought to be different. Each one of these would have, for instance, a different combination of baryon number and lepton number. These aren’t expected to make a difference in General Relativity, but these numbers are conserved in every particle interaction we’ve ever witnessed. If we understand the quantum physics of black holes correctly — and that’s in and of itself a debatable prospect — we’d fully expect that the information from the particles the black hole is made of is, somehow, encoded on the event horizon of the black hole itself.

Encoded on the surface of the black hole can be bits of information, proportional to the event horizon’s surface area. When the black hole decays, it decays to a state of thermal radiation. As matter and radiation fall into the black hole, the surface area grows, enabling that information to be successfully encoded. When the black hole decays, entropy will not decrease, but rather will remain constant, as Hawking radiation is an entropy-conserving (adiabatic) process.

This is an example of the black hole information paradox: there are quantum bits of information that went into this black hole, and if the entropy of the Universe is never to decrease, you must somehow preserve, rather than destroy, that information. In other words, there should be some sort of “quantum memory” that persists, imprinted somehow onto the black hole itself. The natural place for that is the event horizon, as the entropy of a black hole — and also, the amount of information you can encode onto one — is proportional to the event horizon’s surface area.

If your black hole is made of antimatter, there should be some property encoded on its event horizon that somehow remembers the quantum properties of each particle that went into making this black hole. Each particle that crosses over from outside-to-inside the event horizon, from the perspective of an external observer, has that particle’s last moments “smeared out” over the surface of the black hole. Whenever radiation is emitted from the black hole, whether electromagnetic Hawking radiation from decay or gravitational radiation from merging with another large mass, the information that went into the black hole should be preserved when information-containing quanta are emitted again.

In the far future, there will be no more matter around black holes, but instead their emitted energy will be dominated by Hawking radiation, which will cause the size of the event horizon to shrink. The transition from “growing” to “decaying” black holes will occur whenever the accretion rate drops below the mass loss rate due to Hawking radiation, an event estimated to occur some ~10^20 years in the future. How the information that went into making the black hole gets encoded into the outgoing radiation, or whether that’s even the case, has not yet been determined.

Still, those differences are going to be very, very subtle, and they’re also beyond our present ability to not only detect, but to even predict how we would observe them. This is a very poorly understood realm of physics, where theoretical work is still being done. For this problem, observable, measurable signatures remain ambiguous and have not been extracted yet. And the properties of the gravitational waves emitted from an inspiral and merger — itself a phenomenon intrinsic to General Relativity — may not have any quantum signature that we would recognize as “information” imprinted on them.

That’s one of the big open questions in all of physics: is there a fundamentally quantum theory of gravity, and if so, how does its behavior differ from our “classical” theory of gravity: General Relativity? These are the types of questions we’d have to answer in order to see a difference between two merging matter-based black holes versus a merging matter-based and antimatter-based black hole. There could be a different polarization encoded in the radiation, and if we can break that radiation down into individual quanta — discrete gravitons for gravitational waves, just like light waves can be broken down into discrete photons — we might discover different properties like spin values and their correlations, as well as potentially additional quantum numbers.

A series of particles moving along circular paths can appear to create a macroscopic illusion of waves. Similarly, individual water molecules that move in a particular pattern can produce macroscopic water waves, individual photons make the phenomenon we perceive as light waves, and the gravitational waves we see are likely made out of individual quantum particles that compose them: gravitons.

But what if the Universe surprises us?

All of this assumes, of course, that antimatter gravitates the way that normal matter does: attractively, in proportion to its rest mass. But in physics, there are multiple ways to define mass, and these different definitions are not necessarily related to one another. For example:

• There’s a mass, m, in F = ma, which dictates how an object accelerates when a force is applied to it.
• There’s a mass, m, in E = mc², which dictates how much energy a massive particle at rest has inherent to it, as well as how much energy it takes to create it and how much energy is released if it’s destroyed.
• And there’s a mass, m, that shows up for any gravitational effects; it’s the m in Newton’s F = GmM/r², and this m also shows up in the significantly more complex, Einsteinian version of that equation.

For antimatter, we know that the m that goes with F = ma exhibits identical behavior for both matter and antimatter for the known three quantum forces: electromagnetism, plus the strong and weak nuclear forces. For the creation and destruction of both matter and antimatter, we know that the m that goes with E = mc² behaves identically, whether it’s matter or antimatter we’re talking about.

But for gravitation? We can only assume that there’s an equivalence between what we call inertial mass — the m in both F = ma and E = mc² — and gravitational mass. But, thus far, that equivalence has only been tested for matter, never for antimatter.

The identical behavior of a ball falling to the floor in an accelerated rocket (left) and on Earth (right) is a demonstration of Einstein’s equivalence principle. If inertial mass and gravitational mass are identical, there will be no difference between these two scenarios. This has been verified to ~1 part in one trillion for matter, and was the thought (Einstein called it “his happiest thought”) that led Einstein to develop his general theory of relativity.

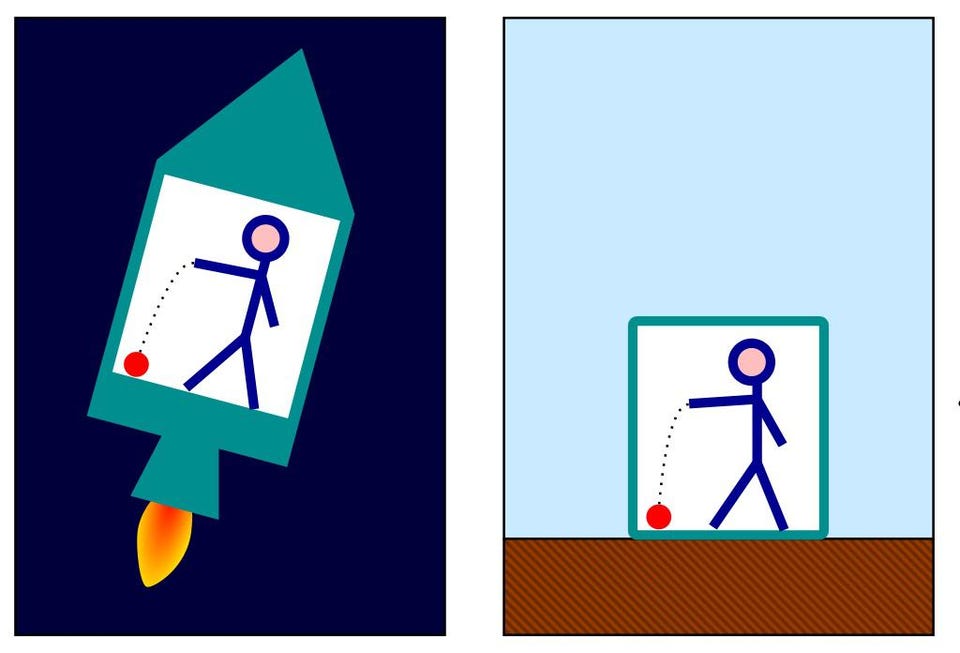
The way we’ve tested it is through an apparatus known as a torsion balance: where a mass that’s allowed to rotate is placed very close to a fixed, larger mass, allowing the smaller one to rotate due to gravitational attraction. This experiment, named after Loránd Eötvös, sufficiently demonstrated that what we call “inertial mass” (the mass from F = ma) and gravitational mass (from gravitational attraction) are indeed the same as one another. This is demanded, in General Relativity, by Einstein’s equivalence principle.

But for antimatter, we’ve never measured its gravitational attraction at all. In truth, we don’t even know whether it falls “down” in a gravitational field the same way normal matter does. No matter how compelling the theoretical arguments are in favor of this, physics remains an experimental science, and until we have the decisive evidence, we cannot be certain of the conclusions.

There are experiments going on right now designed to measure exactly this. At a lab known as the antimatter factory at CERN, there are numerous collaborations striving to isolate neutral anti-atoms at rest, and to measure which direction they fall when placed in Earth’s gravitational field. Although the overwhelming expectation is that they’ll fall down at the same rate as normal matter, there’s always the possibility they may not.

The ALPHA-g detector, build at Canada’s TRIUMF facility, will be oriented vertically and filled with neutral antiatoms confined by electromagnetic fields. When the fields release, most anti-atoms will randomly fly away, but a few that happen to be at rest will have the opportunity to move solely under the influence of gravity. If they fall up, everything will change.

If, instead of falling down, neutral anti-atoms fall “up”, it would change so much of what we know is possible in the Universe. If antimatter’s gravitational behavior was instead equal to the negative of its inertial behavior, a remarkable set of consequences would ensue.

• Antimatter would be gravitationally repelled by normal matter, rather than attracted to it.
• Antimatter would function as “negative mass,” which would enable technologies that depend on its (currently speculative) existence, such as artificial gravity.
• And, so long as the equation E = mc² is still true, which it must be, that implies that at least gravitationally, antimatter functions as a source of not just negative mass but also negative energy, which would make warp drive, via the Alcubierre drive, a realistic physical possibility.

As far as what we expect, we have every reason to believe that antimatter gravitates just as regular matter does, rather than anti-gravitates. We ought to anticipate that only at the quantum level would there be differences between an antimatter black hole and a matter-based black hole. But at its heart, physics is an experimental science. Until we get the definitive results, we’d be utter fools to discount anything that experiment hasn’t already ruled out.

Send in your Ask Ethan questions to startswithabang at gmail dot com!