Ask Ethan #91: Does Quantum Gravity Need String Theory?
If String Theory has nothing to do with reality, what are our options?
“I just think too many nice things have happened in string theory for it to be all wrong. Humans do not understand it very well, but I just don’t believe there is a big cosmic conspiracy that created this incredible thing that has nothing to do with the real world.” –Edward Witten
There’s no doubt that, from a mathematical viewpoint, there’s no shortage of incredible, beautiful, elegant frameworks out there. But not all of them are relevant for our physical Universe. It seems like for every brilliant idea that accurately describes what we can observe and measure, there’s at least one equally brilliant idea that attempts to describe the same things that turns out to be completely wrong. After an outcry last week for a column on one of String Theory’s alternatives, I found this gem from Kent as I sifted through the questions and suggestions for the week:
I hope you do have time to devote an article to quantum gravity sometime soon. In particular, I would like to know if any progress has been made in this field in the last five to ten years. From my non-expert perspective, it seems like the field has been stuck for a while since since string theory started falling out of favor for testability reasons and having 10^500 possible solutions. Is this true, or is there progress being made behind the scenes that just hasn’t gotten as much main-stream press?
First off, there’s a big difference between the idea of quantum gravity, the String Theory solution (or proposed solution), and other alternatives.

Let’s start with the Universe we know and love. On the one hand, there’s General Relativity, our theory of gravitation. It states that rather than being a simple action-at-a-distance that Newton postulated, where all masses in all locations exerted forces on each other inversely proportional to the square of the distance between them, there was a much more subtle mechanism to the whole thing.
Mass, as Einstein established with the equivalence principle and E = mc^2 in 1907, was just one form of energy in the Universe. That energy, in turn, would warp the very fabric of spacetime itself, changing the path that all objects would follow, and curving what an observer would perceive as a Cartesian-like grid. Objects didn’t accelerate due to an unseen force, but rather traveled along the path defined by all the stressed caused by all the different forms of energy in the Universe.
That’s gravity.

On the other hand, we’ve got the other laws of nature: the quantum ones. There’s electromagnetism, which is governed by electrically charged particles, their motions, and is described by the force-carrying particle of the photon, which mediates those interactions and gives rise to the phenomena we associate with electrostatics and magnetism. There are also two nuclear forces: the weak nuclear force, which is responsible for phenomena like radioactive decay, and the strong nuclear force, which binds atomic nuclei together and allows protons and neutrons to exist in the first place.
Calculations for these forces are normally done in flat spacetime, which is how every graduate student first learns quantum field theory. But this is inadequate when we’re in the presence of the curved space mandated by General Relativity.
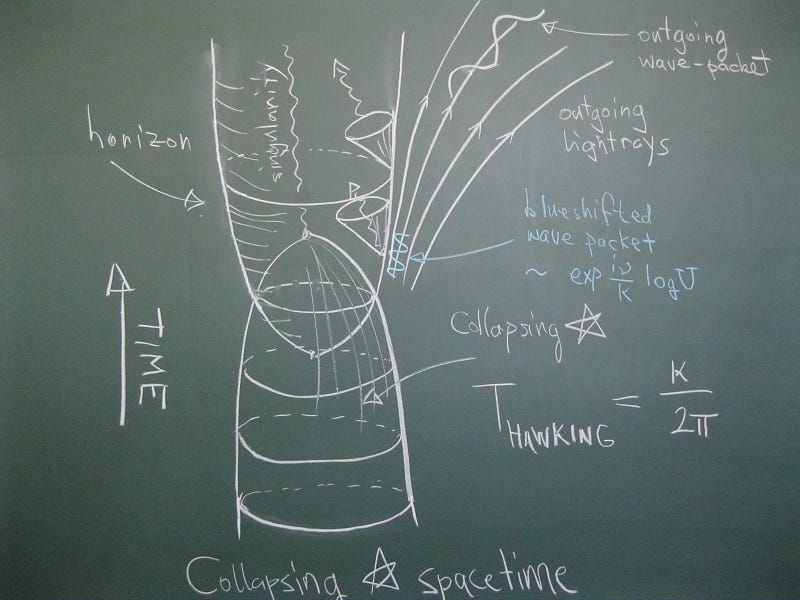
“So,” you reason, “we’ll simply do our quantum field theory calculations in the background of curved space!” This is known as semi-classical gravity, and it’s this type of calculation that allows us to calculate things like Hawking radiation. But even that is only at the event horizon of the black hole itself, not at the location where gravity is truly at its strongest. As Sabine Hossenfelder elegantly explained, there are multiple physical instances where we need a quantum theory of gravity, all having to do with gravitational physics on the smallest of scales: at tiny distances.

What happens, for example, at the central locations of black holes? You might think, “oh, there’s a singularity,” but a singularity isn’t quite so much a point of infinite density, but is more likely an instance where the mathematics of General Relativity returns nonsensical answers for things like potentials and forces. What happens when, say, an electron is passed through a double slit?
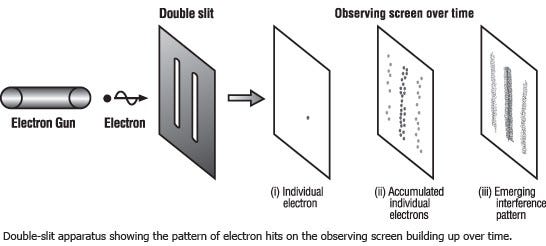
Does the gravitational field pass through both slits? Through one-or-the-other? In General Relativity, there’s no way to account for this.
It’s thought that there must be a quantum theory of gravity to account for these and other problems inherent to a “smooth” theory of gravity like General Relativity. In order to explain what happens at short distances in the presence of gravitational sources — or masses — we need a quantum, discrete, and hence particle-based theory of gravity.
Thanks to the properties of General Relativity itself, there are some things we already know.
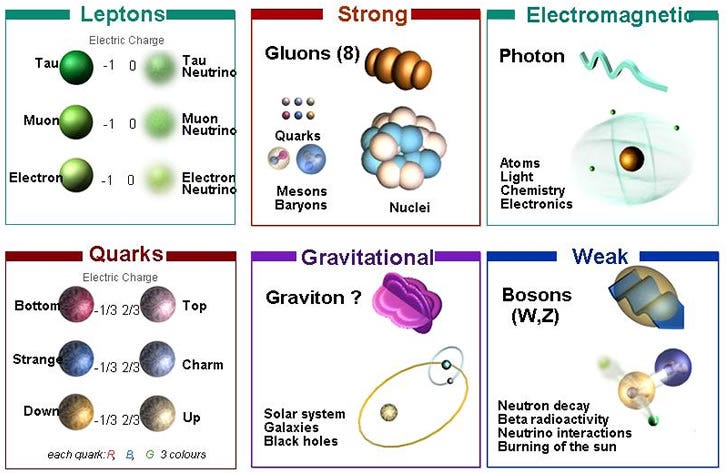
The known quantum forces are mediated by particles known as bosons, or particles with integer spin. The photon mediates the electromagnetic force, the W-and-Z bosons mediate the weak force, while the gluons mediate the strong force. All these types of particles have a spin of 1, which for massive (W-and-Z) particles mean they can take on spin values of -1, 0, or +1, while for massless ones (like gluons and photons), they can take on values of -1 or +1 only.
The Higgs boson is also a boson, although it doesn’t mediate any forces, and has a spin of 0. Because of what we know about gravitation — General Relativity is a tensor theory of gravity — it must be mediated by a massless particle with a spin of 2, meaning it can take on a spin value of -2 or +2 only.
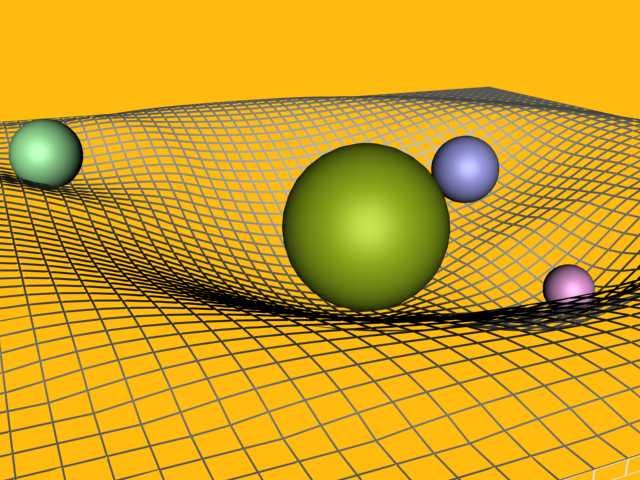
So we already know something about a quantum theory of gravity, before we ever try and formulate one! We know this because whatever the true quantum theory of gravity turns out to be, it must be consistent with General Relativity when we’re not at very small distances from a massive particle or object, just as General Relativity needed to reduce to Newtonian gravity in the weak-field regime.
The big question, of course is how? How do you quantize gravity in a way that’s correct (at describing reality), consistent (with both GR and QFT), and hopefully leads to calculable predictions for new phenomena that might be observed, measured or somehow tested.
The leading contender, of course, is something you’ve long heard of: String Theory.

1.) String Theory. String Theory is an interesting framework — it can include all of the standard model fields and particles, both the fermions and the bosons. It includes also a 10-dimensional Tensor-Scalar theory of gravity: with 9 space and 1 time dimensions, and a scalar field parameter. If we erase six of those spatial dimensions (through an incompletely defined process that people just call compactification) and let the parameter (ω) that defines the scalar interaction go to infinity, we can recover General Relativity.
But there are a whole host of phenomenological problems with String Theory. One is that it predicts a large number of new particles, including all the supersymmetric ones, none of which have been found. It claims to not need to need “free parameters” like the standard model has (for the masses of the particles), but it replaces that problem with an even worse one. When Kent refers to “10^500 possible solutions,” these solutions refer to the vacuum expectation values of the string fields, and there’s no mechanism to recover them; if you want String Theory to work, you need to give up on dynamics, and simply say, “well, it must’ve been anthropically selected.”
But despite what you may have heard, String Theory isn’t the only game in town.

2.) Loop Quantum Gravity. LQG is an interesting take on the problem: rather than trying to quantize particles, LQG has as one of its central features that space itself is discrete. Imagine a common analogy for gravity: a bedsheet pulled taut, with a bowling ball in the center. Rather than a continuous fabric, though, we know that the bedsheet itself is really quantized, in that it’s made up of molecules, which in turn are made of atoms, which in turn are made of nuclei (quarks and gluons) and electrons.
Space might be the same way! Perhaps it acts like a fabric, but perhaps it’s made up of finite, quantized entities. And perhaps it’s woven out of “loops,” which is where the theory gets it name from. Weave these loops together and you get a spin network, which represents a quantum state of the gravitational field. In this picture, not just the matter itself but space itself is quantized. The way to go from this idea of a spin network to a perhaps realistic way of doing gravitational computations is an active area of research, one that saw a tremendous leap forward made in just 2007/8, so this is still actively advancing.
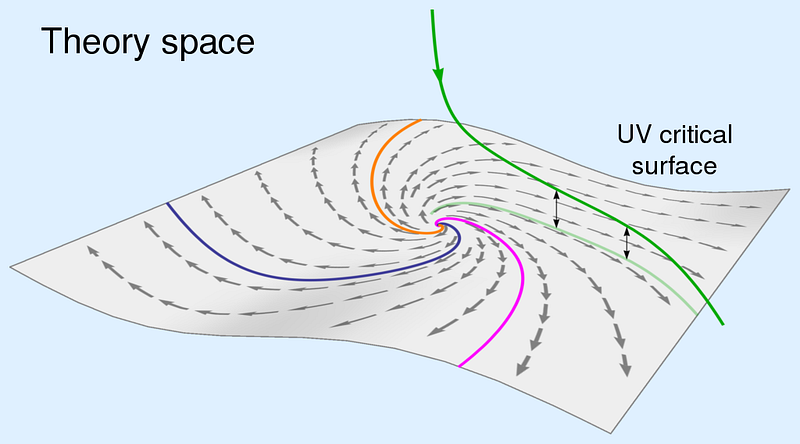
3.) Asymptotically Safe Gravity. This is my personal favorite of the attempts at a quantum theory of gravity. Asymptotic freedom was developed in the 1970s to explain the unusual nature of the strong interaction: it was a very weak force at extremely short distances, then got stronger as (color) charged particles got farther and farther apart. Unlike electromagnetism, which had a very small coupling constant, the strong force has a large one. Due to some interesting properties of QCD, if you wound up with a (color) neutral system, the strength of the interaction fell off rapidly. This was able to account for properties like the physical sizes of baryons (protons and neutrons, for example) and mesons (pions, for example).
Asymptotic safety, on the other hand, looks to solve a fundamental problem that’s related to this: you don’t need small couplings (or couplings that tend to zero), but rather for the couplings to simply be finite in the high-energy limit. All coupling constants change with energy, so what asymptotic safety does is pick a high-energy fixed point for the constant (technically, for the renormalization group, from which the coupling constant is derived), and then everything else can be calculated at lower energies.
At least, that’s the idea! We’ve figured out how to do this in 1+1 dimensions (one space and one time), but not yet in 3+1 dimensions. Still, progress has been made, most notably by Christof Wetterich, who had two groundbreaking papers in the 1990s. More recently, Wetterich used asymptotic safety — just six years ago — to calculate a prediction for the mass of the Higgs boson before the LHC found it. The result?

Amazingly, what it indicated was perfectly in line with what the LHC wound up finding. It’s such an amazing prediction that if asymptotic safety is correct, and — when the error bars are beaten down further — the masses of the top quark, the W-boson and the Higgs boson are finalized, there may not even be a need for any other fundamental particles (like SUSY particles) for physics to be stable all the way up to the Planck scale. Sadly, Richard Dawid’s new book on quantum gravity, String Theory and the Scientific Method — reviewed excellently by Sabine on her blog — doesn’t even mention asymptotically safe gravity.
It’s not only very promising, it has many of the same appealing properties of string theory: quantizes gravity successfully, reduces to GR in the low energy limit, and is UV-finite. In addition, it beats string theory on at least one account: it doesn’t need a whole crapload of new stuff that we have no evidence for! And that’s why it’s my favorite candidate so far.

4.) Causal Dynamical Triangulations. This idea, CDT, is one of the new kids in town, first developed only in 2000 by Renate Loll and expanded on by others since. It’s similar to LQG in that space itself is discrete, but is primarily concerned with how that space itself evolves. One interesting property of this idea is that time must be discrete as well! As an interesting feature, it gives us a 4-dimensional spacetime (not even something put in a priori, but something that the theory gives us) at the present time, but at very, very high energies and small distances (like the Planck scale), it displays a 2-dimensional structure. It’s based on a mathematical structure called a simplex, which is a multi-dimensional analogue of a triangle. A 2-simplex is a triangle, a 3-simplex is a tetrahedron, and so on. One of the “nice” features of this option is that causality — a notion held sacred by most human beings — is explicitly preserved in CDT. (Sabine has some words on CDT here, and its possible relation to asymptotically safe gravity.) It might be able to explain gravity, but it isn’t 100% certain that the standard model of elementary particles can fit suitably into this framework. It’s only major advances in computation that have enabled this to become a fairly well-studied alternative of late, and so work in this is both ongoing and relatively young.
5.) Emergent gravity. Probably the most speculative, recent of the quantum gravity possibilities, it only gained prominence in 2009, when Erik Verlinde proposed entropic gravity, a model where gravity was not a fundamental force, but rather emerged as a phenomenon linked to entropy. In fact, the seeds of emergent gravity go back to the discoverer of the conditions for generating a matter-antimatter asymmetry, Andrei Sakharov, who proposed the concept back in 1967. This research is still in its infancy, but as far as developments in the last 5–10 years go, it’s hard to ask for more than this.
So that’s where we stand on Quantum Gravity today, Kent (and everyone). We’re sure we need it to make the Universe work at a fundamental level, but we’re not sure what it looks like or whether any of these five avenues are going to prove fruitful or not. String Theory is the best studied of the five, Asymptotically Safe Gravity is my personal preference of the five, Loop Quantum Gravity is probably the second most popular among active scientists of the five, and Causal Dynamical Triangulations and Emergent Gravity are the newest ideas undergoing the greatest development at the present.
Thanks to everyone for the submissions for Ask Ethan this week (send yours in here), and thanks also to all who encouraged me to tackle this difficult topic. If you enjoyed this, consider supporting Starts With A Bang on Patreon (supporters get priority selection for Ask Ethan), and I’ll see you back here next week for more wonders of the Universe!
Leave your comments at our forum, and support Starts With A Bang on Patreon!




