Ask Ethan: Could An Unexplained Decay At The LHC Demolish The Standard Model?

Yet, if they only obey the rules that we know, there’s no way to explain why.
One of the greatest puzzles in all of physics is that the laws of nature — as we know them, at least — do a remarkably good job of explaining what matter is and how all the different particles interact with one another. And yet, if these only obey the rules that we know, there’s no way to explain why the Universe is so predominantly made up of matter, rather than antimatter. The only interaction we know of that shows any difference at all between particles and their antiparticle counterparts are the weak interactions, and that difference isn’t nearly enough to explain the Universe we observe. But recently, a new set of experiments have started to show a significant difference between the weak decays of rare particles created at the Large Hadron Collider (LHC) at CERN and what our leading theories would have expected. Could this be an enormous clue towards going beyond the Standard Model? That’s what Rob Krol wants to know, writing in to ask:
“I want know more about the last announcement from the LHCb [collaboration] about CP Violating asymmetry in a charged B meson decay. What [does] this mean and/or this is a hint for new physics beyond the Standard Model??”
This is right at the cutting edge of the frontiers of experimental particle physics, so let’s bring you up to speed on what this new discovery is all about, and then let’s talk about what it might mean.
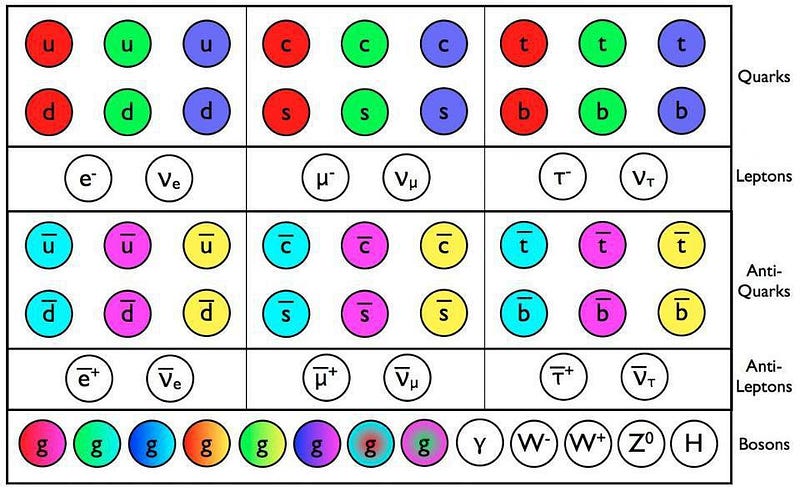
In particle physics, there are six fundamentally different types of quarks in the Standard Model: the up, down, strange, charm, bottom, and top quarks. The six types, known as flavors, are presented in order from lowest to greatest mass. Whenever you create one of the four most massive types of quarks, they’ll rapidly (in ~10^-24 seconds or so) hadronize: become bound into either baryons (combinations of three quarks) or mesons (quark-antiquark pairs). Whatever composite particle arises will then inevitably decay through the weak interaction into a set of particles where that heavy quark has transformed into lighter quark.
Energy and momentum must be conserved, meaning that the “daughter” particles (the decay products) must go off in opposite directions from one another with significant kinetic energies. A series of symmetries must be conserved, which tells us that the total lifetime of the composite particle we’re examining must exactly equal the total lifetime of the “anti-”version of that particle. Each composite particle will have its own unique properties, but certain decay pathways — for example, involving of the decay of a bottom quark into a strange quark — will follow the same physics.
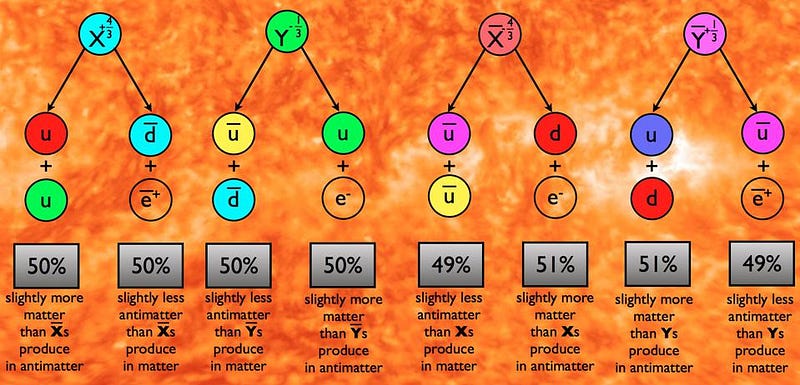
We also know that matter and antimatter can’t obey the exact same rules as one another, otherwise the Universe would have equal amounts of both. That isn’t the Universe we perceive at all, however. For every 1.4 billion photons (particles of light) in the Universe, there’s approximately one proton (and electron) or neutron that exists, and approximately zero (or, at most, ~0.00001) antiprotons and antineutrons.
However, there are ways to create a matter-antimatter asymmetry from an initially symmetric Universe; you just need to obey the three Sakharov conditions. Put forth by physicist Andrei Sakharov in 1968, they simply demand a Universe that:
- has out-of-equilibrium conditions, which comes along naturally in an expanding Universe that started with a hot Big Bang,
- baryon-number violating interactions, which occur in the Standard Model through sphaleron interactions (which create a new lepton for every baryon created),
- and that has both C-violation and CP-violation.
That last criteria is met in the Standard Model — both charge conjugation (swapping particles for antiparticles) and the combination of charge conjugation and parity (mirror-symmetry) symmetries are violated — but not by a great enough amount to explain the Universe we know we have.
One of the places to look for greater amounts of CP-violation than we currently know of is in the decay of the heavier quarks. If you want to have a bottom quark transform into a strange quark, this is a process that is “forbidden” in some sense. “Forbidden” doesn’t mean, in physics, that “this cannot happen,” but rather that the simplest way you’d think of allowing this to occur is forbidden.
For example, a bottom quark has an electric charge of -⅓, and a strange quark has that same electric charge of -⅓. The quarks are two different flavors, with a bottom quark having a “bottomness” of +1 and a strangeness of 0, while a strange quark has a bottomness of 0 and a strangeness of +1.
In theory, you’d imagine that an uncharged weak boson — the Z0 boson — could mediate this transformation, but that’s the exact thing that’s forbidden. Under the Standard Model alone, there’s no such thing as a flavor-changing neutral current (FCNC), which means that you cannot change the “flavor” of your quarks through a neutral (uncharged) exchange of particles. The only way to make that change is through a charged particle: the W-boson.
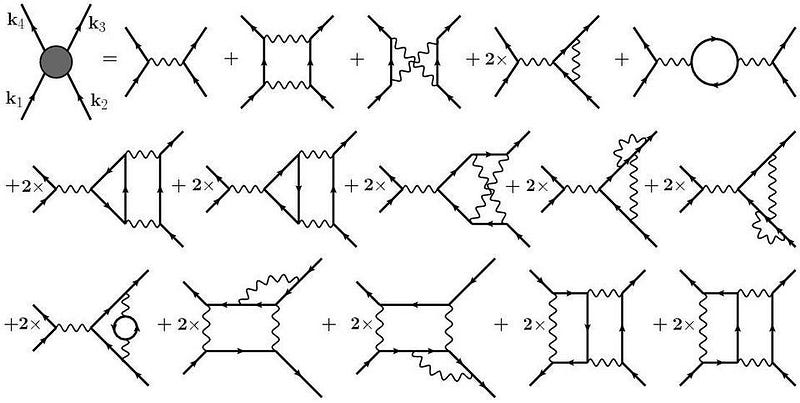
But to make that happen, you have to go to a more complex series of interactions. For example, you can have the bottom quark first decay to a charm quark, and then have the charm quark decay to a strange quark. Or you can “loops” in a diagram that contributes significantly at the electroweak scale. Or, most excitingly, you might have new physics that appears at some energy scale: this is part of the reason we examine these rare, suppressed decays in such detail. It’s important to remember that the LHC isn’t just looking for new fundamental particles, like the Higgs boson, but also:
- for new composite particles, which it’s discovered about 50 of so far,
- and for rare decays of existing particles, which it seeks to measure exquisitely.
By doing this, we can isolate and identify any possible signatures of new physics: physics that the Standard Model, on its own, can’t explain. (This is also part of the reason why building a new, more energetic particle collider will always be interesting as an experimental probe for new physics, even if all our leading theoretical ideas turn out to be ill-motivated.) For this, it isn’t the two main detectors — ATLAS and CMS — that are the best tools for the job, but rather a detector explicitly designed to measure particles that start off their life containing a bottom (b) quark: the LHCb detector and its associated scientific collaboration.

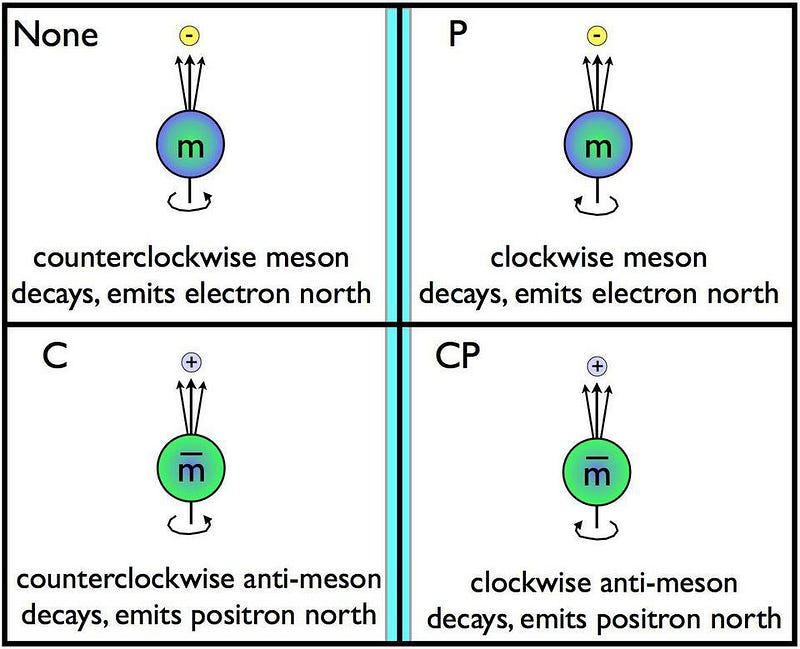
One of the best places to look for new physics that might affect the problem of the matter-antimatter asymmetries is with b-quark containing hadrons that exhibit CP-violation. In general, you can think of CP-violation as follows:
- you imagine a composite particle that’s unstable (so it will decay),
- and you imagine its antimatter version: it’s also unstable (and will decay),
- now also imagine reflecting the antimatter version in a mirror,
- and if any properties at all are different between the regular particle version and the mirrored+antiparticle version, congratulations: you have violated CP.
One of the most common ways that CP is violated, in practice, is when you observe what’s known as a different branching ratio or decay amplitude. The total lifetime of the particle and mirrored+antiparticle versions have to be the same. The corresponding decay pathways must all be allowed. But the fraction of particles that decays via one pathway is allowed to be different from the fraction of particles that decays via a different pathway.
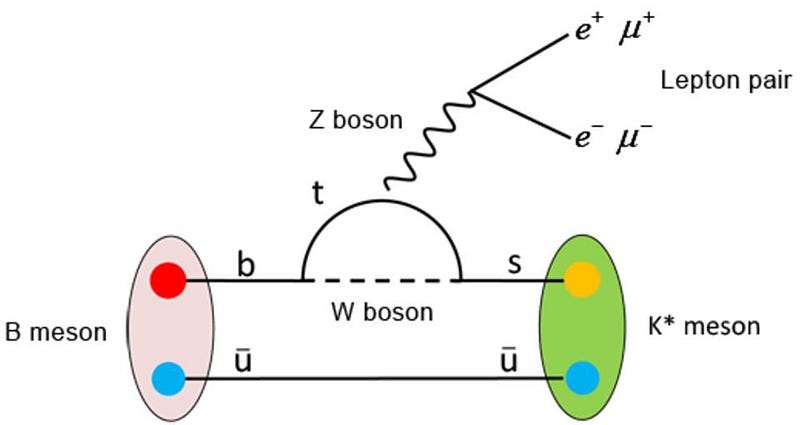
This can occur not only for a particle and its antiparticle, but for two different particles that contain the same heavy quark (like a b or anti-b quark) and the same physics underlying their decay pathways. For about ~20 years, one such example that’s been under investigation is the branching fractions and CP asymmetries of B-mesons, which are quark-antiquark combinations that contain one b or anti-b quark, as they decay into a kaon (which contains a strange quark) and a pion (which contain up and down quarks, only).
In particular, a neutral B-meson, known as a B⁰, can either decay into a positive kaon (K+) and a negative pion (π-) or a neutral kaon (K⁰) and a neutral pion (π⁰). Similarly, a positively charged B-meson, known as a B+, can either decay into a positive kaon and a neutral pion (K+π⁰) or a neutral kaon and a positive pion (K⁰π+). In theory, the amplitudes should obey certain relations that apply to the Standard Model, like isospin symmetry, but — as the LHCb collaboration has concluded — measurements show our observations to be inconsistent with those expectations. Something weird is going on.
There are a total of four decays that have to be considered together in order to understand what’s happening. You have, remember, the following four decays that you need to measure:
B⁰ → K+π-,
B⁰ → K⁰π⁰,
B+ → K+π⁰, and
B+ → K⁰π+.
You have to measure three things for each one: what is the CP-asymmetry for each of these decays, what is the branching fraction (i.e., what fraction of the “parent particles” decay in this particular fashion) of each decay pathway, and what are the overall lifetimes of these parent particles, B⁰ and B+?
Once you make those measurements, you can compare them to your theoretical predictions. The enormous advantage of the LHCb experiment is that it can create more of these parent particles — the B⁰ and B+ — than any other apparatus, and it’s specifically designed to measure the energy and momenta of every decay product that comes out of them.
What you’d expect is that the CP-asymmetry of the decaying B0 and B+ particles would be identical to one another. In particular, if you measured the CP-asymmetry of, say, the B+ → K+π⁰ decay and subtracted the CP-asymmetry of the B⁰ → K+π- decay, you’d expect to get 0. The latter asymmetry had been measured previously, and was known to a very small error: the CP-asymmetry the decaying B⁰ was measured to be −0.084, with a minuscule uncertainty of just ±0.004.
What the new announcement by the LHCb collaboration represents is the best-ever measurement of the former (B+ → K+π⁰) decay, which previously had a very large uncertainty associated with it. The new CP-asymmetry of a decaying B+, with the new LHCb data included, is now +0.031, with an uncertainty of only ±0.013.
You don’t need to be a math whiz to realize that if you subtract these two asymmetries from one another, you get a large, non-zero value; one that’s statistically significant at a level that’s greater than an unprecedented 8 standard deviations from the null hypothesis. Whatever’s going on, it’s not what the Standard Model predicts.
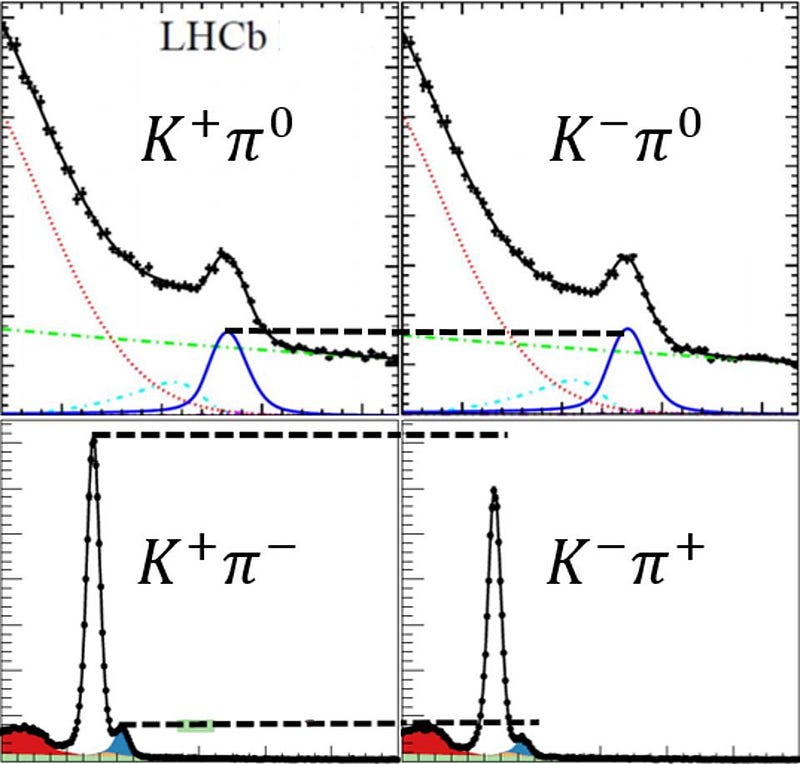
This is quickly becoming known as simply the “Kπ” puzzle, since it’s most apparent in bottom-quark containing mesons that decay to kaons and pions. There are errors that are well-quantified from three sources: statistics, systematics, and external input uncertainties; all of them are far too insignificant to explain this discrepancy. Either something that we haven’t calculated properly that’s still within the Standard Model is responsible for this — which seems exceedingly unlikely — or we’re encountering new physics beyond the Standard Model when it comes to the Kπ puzzle.
It’s very clear that the amplitude of these decays, which should be equal to one another, are not, in fact, equal: it’s reached a major significance of 8 standard deviations, which is enormous in a field where a significance of 5 is considered the “gold standard.” As the LHC ramps back up for its next data run, we fully anticipate that not only will the significance of this result continue to increase, but we may start to see unexpected, non-standard effects in other decays as well. Although many creative theorists will no doubt come up with a multitude of potential explanations, it’s the experimental data that will always drive us forward. In physics, as in all sciences, the Universe itself is the ultimate arbiter of what’s truly real.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.