Ask Ethan: How Does A Photon Experience The Universe?

If you think you have problems today, be glad you’re not moving at the speed of light.

Special relativity, even though it’s over 100 years old, is still one of the most puzzling and perplexing discoveries about the nature of the Universe itself. The (Newtonian) laws of physics that we’re used to here on Earth remain valid under almost all conditions, but not if you’re moving close to the speed of light. Clocks run at different rates, distances appear altered, and objects themselves change color dependent on their speed relative to you. Yet, at the same time, relativity declares that the laws of physics are the same and invariant for all observers, regardless of their motion. So what does this mean for a photon, which itself moves at the speed of light? Patreon supporter Rob Hansen wants to know, asking:

Relativity says all inertial frames of reference are equally valid and true. From a photon’s point of view the entire cosmos is flattened into a two-dimensional timeless plane. Imagine I place an apple on my desk, then a while later replace it with a banana. How does the photon perceive my desk to be, when it’s all flattened into a plane without any sense of time?

Let’s imagine what happens in three cases: for someone at rest, for someone moving close to the speed of light, and then that last leap, to a photon itself.

1.) An observer at rest. There you are, at rest relative to your surroundings, looking at the Universe before you. Your clock ticks by at the same rate it always does: one second per second. You look out at your environment, and the clocks you see there are all running at the same speed as yours: one second per second. Objects appear to be the colors that they actually are, the sizes that they actually are, and nothing behaves counterintuitively. Whether you look behind you or in front of you, everything seems exactly as it should.

This is your conventional experience with the world. Here on Earth, typical human speeds are minuscule compared to the speed of light. Even aboard an airplane moving at nearly the speed of sound, you’re only traveling at 0.0001% the speed of light. From a position at rest relative to your surroundings, you see the three-dimensional Universe in a fashion that’s consistent for everyone.

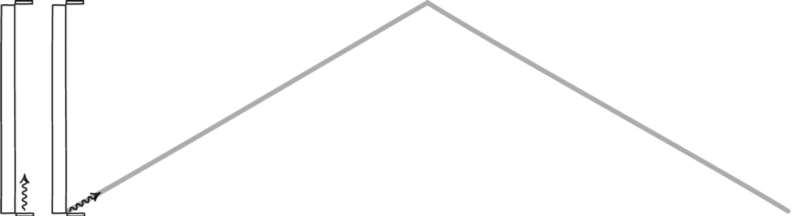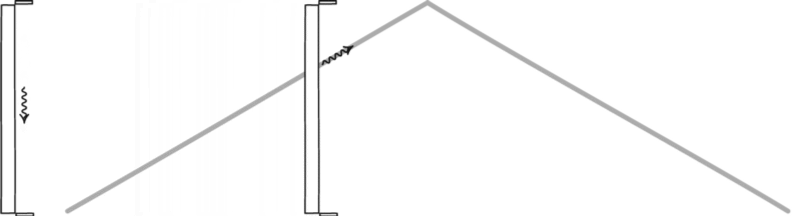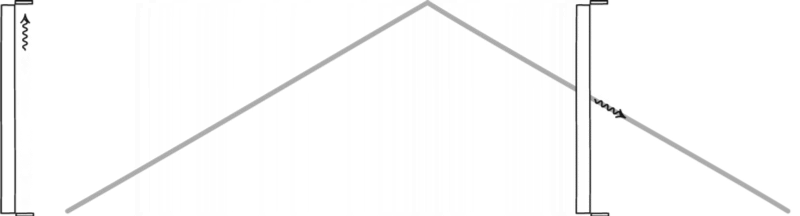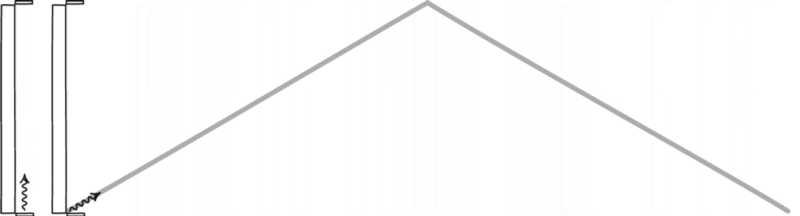
2.) An observer moving close to the speed of light. Here’s where things start to get weird. Imagine you’re traveling close to the speed of light, in one particular direction, relative to your otherwise stationary surroundings. The first difference you’d notice is in terms of time. The clock traveling with you would still travel at the same rate you were used to: one second per second. But the clocks in the environment? They all appear to run slow.

The reason for this is simple: space and time aren’t independent entities, but inextricably interrelated ones. Every object in the Universe moves through spacetime so that it’s total motion adds up to a certain value. When you’re stationary with respect to space, your motion is 100% through time, and time passes for everyone at one second per second. But when you increase your motion through space, you decrease your motion through time. Relative to you, the environment’s clocks appear to run slow, because the entire environment appears to be moving.

Moving at high speeds relative to your environment has a number of other effects that you experience as well. Lengths and distances get contracted along your direction-of-motion, which is a similar requirement of relativity. Because the speed of light must be invariant for all observers in all reference frames, if time appears to pass more slowly (there’s less time), then distances need to contract (there needs to be less distance) in order for the speed of light to remain constant.

In addition to length contraction and time dilation, there’s yet another effect that comes into play: redshift and blueshift. In the direction that you’re moving — or, alternately, the direction the environment appears to be moving toward you — the light’s wavelength appears compressed, or shorter and bluer. In the opposite direction, any light you receive will appear stretched, with longer wavelengths and redder colors.

The faster you move, the worse these effects get. Distances of physical objects contract more and more severely, and even the electric fields produced by charged particles contract along their direction-of-motion. Time dilates more severely; unstable particles produced in our upper atmosphere (muons) can travel the full 100 kilometers down to Earth’s surface, even though their lifetime of 2.2 microseconds indicates that they shouldn’t make it even 1 kilometer if they were moving at the speed of light. And redshifts and blueshifts are so severe at ultra-high speeds that even photons left over from the Big Bang, having an energy corresponding to just 3 K at present, can spontaneously produce new particles when they collide with protons via E = mc2 at high enough blueshifts.

These effects of time dilation, length contraction, and redshift/blueshift get more severe the closer to the speed of light you get. But there’s a limit.

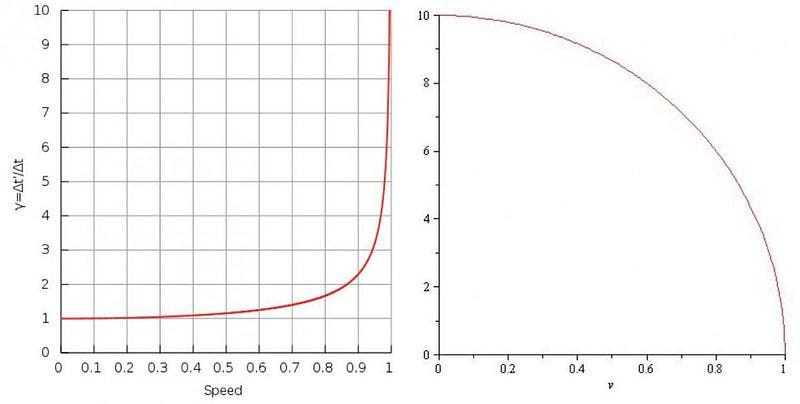
3.) An observer moving at the speed of light. This is where the real trouble starts. If you simply took progressively more and more steps towards the speed of light, you’d just experience more severe amounts of time dilation, length contraction, and redshifts and blueshifts relative to yourself. Apples would appear yellow, blue, and then ultraviolet as you moved towards them; bananas would appear orange, red, and then infrared as you moved away from them.

But if you actually reached the speed of light — which you’d experience if you were a photon — time and space would no longer behave as you were used to them behaving. If you moved at the speed of light relative to your surroundings, then your surroundings would appear to have no time pass at all relative to you. Because its motion would appear to be at the speed of light, there could be no additional motion allowing a photon to move relative to your surroundings: a clock would be impossible.

All of the equations of special relativity break down at the speed of light. Time doesn’t pass for your surroundings. All distances along your direction-of-motion contract down to zero. Redshifts and blueshifts occur in infinite amounts.

It might be very tempting to intuit, based on this, that since the distances along your direction-of-motion contract down to zero, the Universe becomes two-dimensional to you. That time doesn’t pass — so it’s timeless — and it would appear just as a plane: with infinite length contraction. And therefore, that a photon, seeing you replace an apple with a banana on your desk, would experience the presence of both at once.

But what happens in reality is, perhaps, even more surprising.

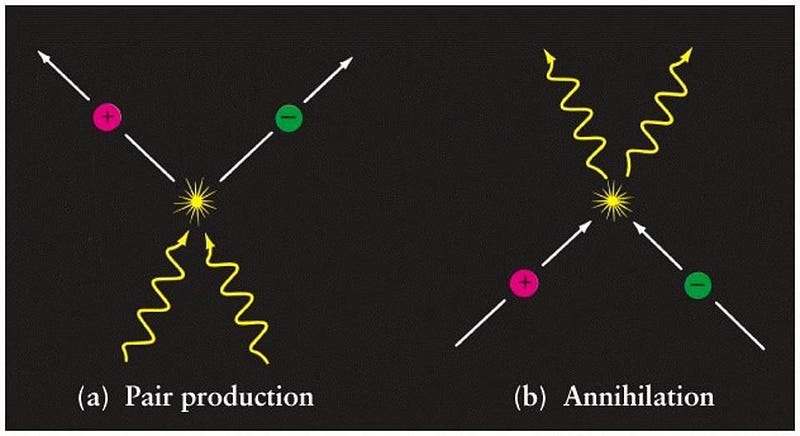
A photon cannot see or experience anything, as it turns out. It’s true that time doesn’t pass for a photon: in relativity, it represents what we call a null geodesic. It travels from its point-of-origin to its point-of-termination: from where an interaction creates (or emits) it to where another interaction destroys (or absorbs) it. This is exactly what happens whether it’s emission/absorption, emission/reflection, a scattering interaction, or any type of interplay with another particle.

When you ask what a photon would “see,” you are assuming that it’s possible for something to interact with a photon and for the photon to experience that interaction somehow. Yet all it experiences are two “things” during its existence: the interaction that creates it and the interaction that destroys it. Whether there is a photon that persists after the destruction, such as via scattering or reflection, is immaterial. All that a photon experiences are those two events at the endpoints of the photon’s journey.

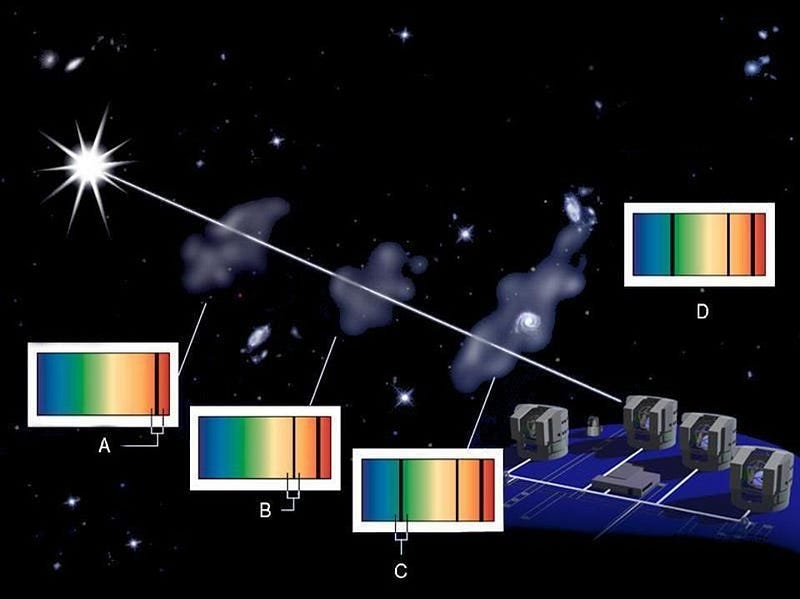
This is why we demand that we do our relativity calculations in an inertial reference frame. We can calculate how a photon redshifts or blueshifts if we use a reference frame moving slower than the speed of light, but not from the photon’s reference frame. From an inertial frame of reference, we can calculate the distance between its emission and absorption point, but not from the photon’s reference frame. We can calculate its light-travel time, from any inertial reference frame, but not from the photon’s reference frame.

The problem is that the photon’s reference frame isn’t an inertial reference frame: In an inertial reference frame, there are physical laws which don’t depend on the motion of anything external to the system. Yet for a photon, the physical rules it obeys depend exclusively on everything going on external to it. You cannot calculate anything meaningful for it from the photon’s reference frame alone.

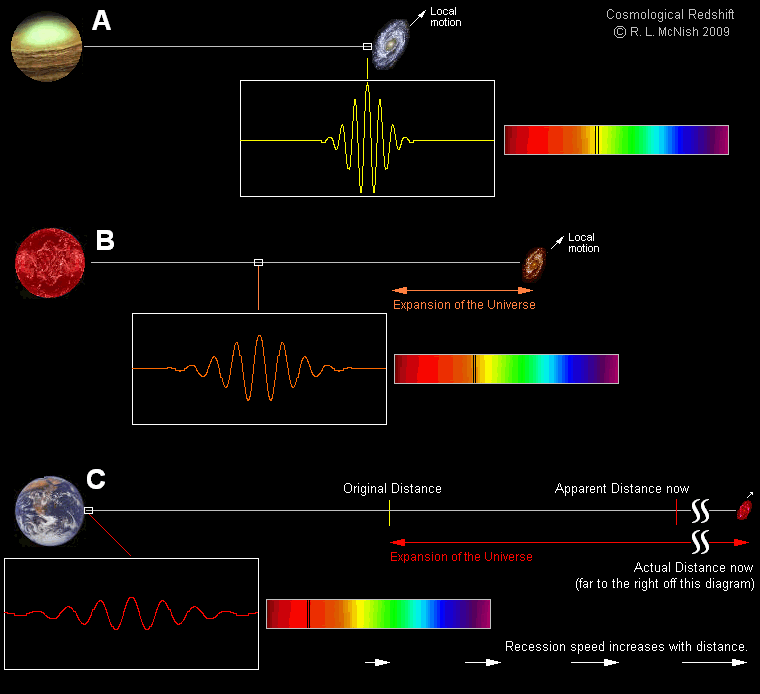
This is because photons — and all particles that travel at the speed of light — lack a rest mass. That rest mass is what’s required to live in an inertial reference frame: mass and how that mass is distributed provide us with our definition of inertia! A photon cannot see the Universe at all, because seeing requires interacting with other particles, antiparticles, or photons, and once such an interaction occurs, that photon’s journey is now over.

According to any photon, its existence is instantaneous. It comes into existence with an interaction and it winks out of existence with another interaction. This could be emission from a distant star or galaxy and its arrival at your eye, and it doesn’t matter whether it’s from our own Sun or an object tens of billions of light years away. When you move at the speed of light, time ceases to pass, and your lifetime only lasts an instant.

Physicists often joke that time is what we have to keep everything from happening all at once. But the real joke is on any object that’s so unfortunate to experience the Universe at light speed. If you were so unlucky, you wouldn’t see, hear, or feel anything. You wouldn’t be able to experience existence at all.

Send in your Ask Ethan questions to startswithabang at gmail dot com!