Ask Ethan: How Does Spinning Affect The Shape Of Pulsars?

They’re the fastest rotators of all. So how distorted are they?
There are very few objects in the Universe that stand still; almost everything we know of rotates in some way. Every moon, planet, and star we know of spins on its own axis, meaning that there’s no such thing as a truly perfect sphere in our physical reality. As an object in hydrostatic equilibrium spins, it bulges at the equator while compressing at the poles. Our own Earth is an additional 26 miles (42 km) longer along its equatorial axis than its polar axis due to its once-a-day spin, and there are many things that spin more quickly. What about the objects that spin the fastest? That’s what our Patreon supporter Jason McCampbell wants to know:
[S]ome pulsars have incredible spin rates. How much does this distort the object, and does it shed material this way or is gravity still able to bind all of the material to the object?
There’s a limit to how quickly anything can spin, and while pulsars are no exception, some of them are truly exceptional.

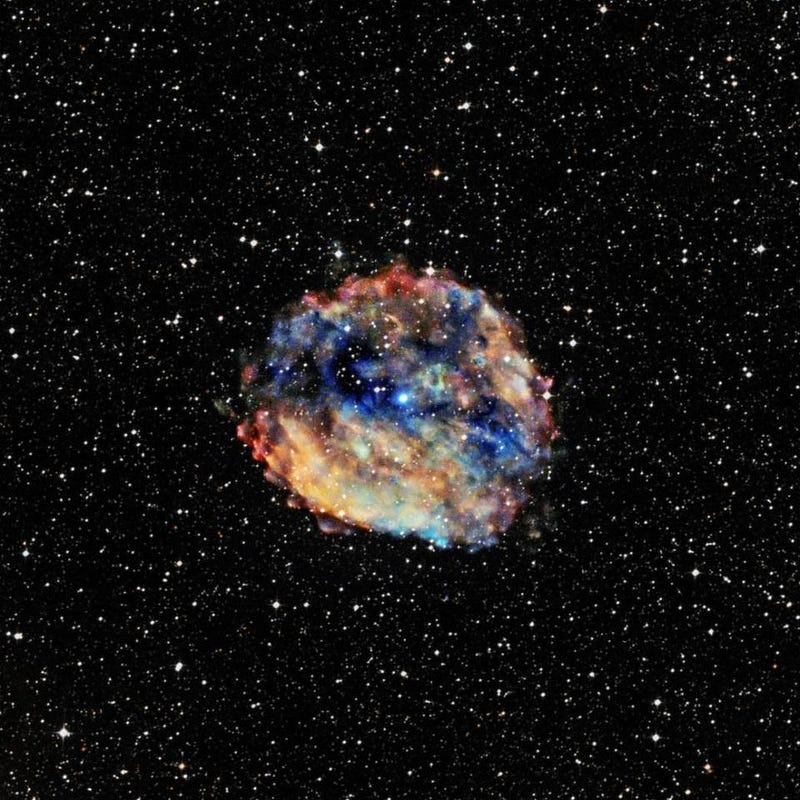
Pulsars, or rotating neutron stars, have some of the most incredible properties of any object in the Universe. Formed in the aftermath of a supernova, where the core collapses down to a solid ball of neutrons exceeding the mass of the Sun but just a few kilometers in diameter, neutron stars are the densest known form of matter of all. Although they’re called “neutron stars,” they’re only about 90% neutrons, so when they rotate, the charged particles composing them move rapidly, generating a large magnetic field. When surrounding particles enter this field, they get accelerated, creating a jet of radiation emanating from the neutron star’s poles. And when one of these poles points at us, we see the “pulse” of the pulsar.

Most of the neutron stars out there don’t appear as pulsars to us, since most of them aren’t coincidentally aligned with our line-of-sight. It may be the case that all neutron stars are pulsars, but we only see a small fraction of them actually pulsing. Nevertheless, there exists a huge variety of rotational periods found in spinning neutron stars that are observable.

Ordinary pulsars, which includes the overwhelming majority of young pulsars, take anywhere from a few hundredths of a second to a few seconds to make a complete rotation, while older, faster, “millisecond” pulsars spin much faster. The fastest known pulsar rotates 766 times per second, while the slowest one ever discovered, at the center of the 2,000 year old supernova remnant RCW 103, takes an incredible 6.7 hours to make a complete rotation about its axis.
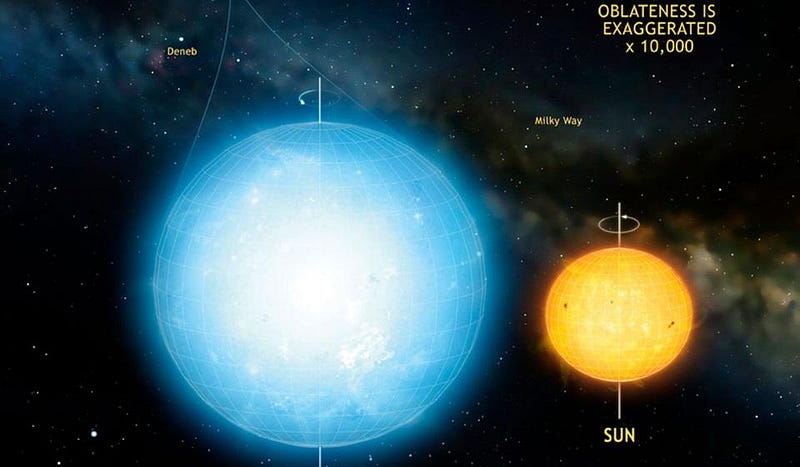
A couple of years ago, there was a false story going around that a slowly-rotating star was now the most spherical object known to humanity. Unlikely! While the Sun is very close to a perfect sphere, just 10 km longer in its equatorial plane than the polar direction (or just 0.0007% away from a perfect sphere), that newly-measured star, KIC 11145123, is more than twice the size of the Sun but has a difference of just 3 km between the equator and the poles.
While a 0.0002% departure from perfect sphericity is pretty good, the slowest-rotating neutron star, known as 1E 1613, has them all beat. If it’s about 20 kilometers in diameter, the difference between the equatorial and the polar radii is approximately the radius of a single proton: a less-than-one-trillionth of 1% flattening. That is, if we can be certain that it’s the rotational dynamics of the neutron star are what dictate its shape.
But that may not be the case, and this matters tremendously when we look at the other side of the coin: to the fastest-rotating neutron stars.

Neutron stars have incredibly strong magnetic fields, with normal neutron stars coming in at approximately 100 billion Gauss and magnetars, the most powerful ones, at somewhere between 100 trillion and 1 quadrillion Gauss. (For comparison, the Earth’s magnetic field is about 0.6 Gauss.) While rotation works to flatten a neutron star into a shape known as an oblate spheroid, the magnetic fields ought to have the opposite effect, lengthening the neutron star along the rotating axis into a football-like shape known as a prolate spheroid.
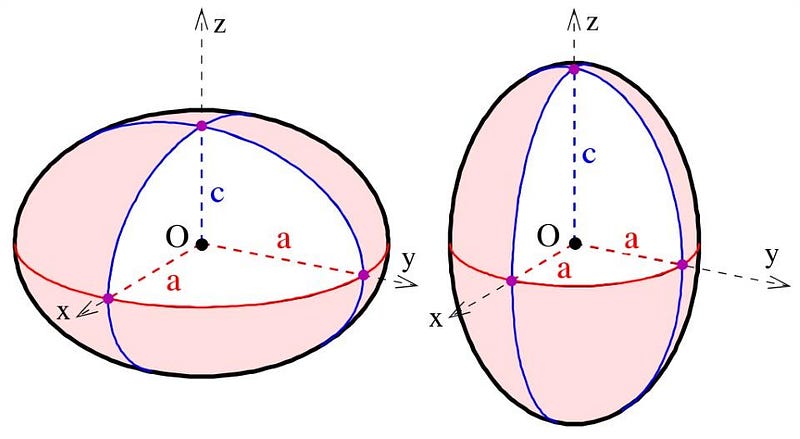
Owing to gravitational wave constraints, we are certain that neutron stars are deformed by less than 10–100 centimeters from their rotationally-caused shape, meaning that they are perfectly spherical to within approximately 0.0001%. But the real deformations should be a lot smaller. The fastest neutron star rotates with a frequency of 766 Hz, or a period of just 0.0013 seconds.
While there are many ways to attempt to calculate the flattening for even the fastest neutron star, with no agreed-upon equation, even this incredible rate, where the equatorial surface moves at about 16% the speed of light, would result in a flattening of only 0.0000001%, give or take an order of magnitude or two. And this is nowhere close to escape velocity; everything on the surface of the neutron star is there to stay.

When two neutron stars merged, however, that may have provided the most extreme example of a rotating neutron star (post-merger) that we’ve ever encountered. Under our standard theories, these neutron stars ought to have collapsed into a black hole past a certain mass: approximately 2.5 times the mass of the Sun. But if these neutron stars rotate rapidly, they can remain in a neutron star state for some time, until enough energy is radiated away via gravitational waves to reach that critical instability. This can increase the mass of an allowable neutron star, at least, temporarily, by up to an additional 10–20%.
When we observed the neutron star-neutron star merger and the gravitational waves from it, this is exactly what we believe happened.
So, post-merger, what was the rotation rate of the neutron star? How distorted was its shape? And what types of gravitational waves do post-merger neutron stars emit in general?
The way we’ll arrive at the answer involves a combination of examining more events in a variety of mass ranges: below a combined mass of 2.5 solar masses (where you should get a stable neutron star), between 2.5 and 3 solar masses (like the event we saw, where you get a temporary neutron star that becomes a black hole), and above 3 solar masses (where you go directly to a black hole), and measuring the light signals. We’ll also learn more by catching the inspiral phase faster, and being able to point towards the anticipated source in advance of the merger. As LIGO/Virgo and other gravitational wave detectors both come online and get more sensitive, we’ll get better and better at this.

Until then, know that neutron stars, despite what you might think from their rapid rotation, are extremely rigid due to their unmatched densities. Even with their very strong magnetic fields and their relativistic spins, they’re very likely a more perfect sphere than anything else we’ve ever found, macroscopically, in the entire Universe. Unless individual particles turn out to be more perfect spheres (and they may), the slowest-rotating, lowest-magnetic field neutron stars are the places to look for the most spherical, naturally occurring objects of all. By time you get to a long-lived, stable neutron star, all it’s going to do over time is slowly change its rotation rate. Everything on it, as far as we can tell, is there to stay.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.



