Ask Ethan: Is Einstein’s Cosmological Constant The Same As Dark Energy?

It might have been Einstein’s greatest blunder, but it’s our leading theory today.

One of the most mysterious components in the entire Universe is dark energy, which — if we’re being honest with ourselves — wasn’t supposed to exist. We had assumed, quite reasonably, that the Universe was a balancing act, with the expansion of the Universe and the gravitational effects of everything within it fighting against one another. If gravity won, the Universe would recollapse; if the expansion won, everything would fly away into oblivion. And yet when we made the critical observations in the 1990s and beyond, we found that not only is the expansion winning, but the distant galaxies we see speed away from us at faster and faster rates as time goes on. But is this really a novel idea, or it is simply the resurrection of what Einstein once called his greatest blunder: the cosmological constant? That’s the question of Boris Petrov, who asks:

“Is Einstein’s cosmological constant [the same] as dark energy? Why has, over time, the term “dark energy” replaced the original term “cosmological constant?” Are the two terms identical or not, and why?”

Okay, so there are a lot of questions there. Let’s back up all the way to Einstein’s original idea, the cosmological constant, for better and for worse.

You have to remember that back when Einstein was working on a theory of gravity to replace and supersede Newton’s law of universal gravitation, we didn’t yet know very much about the Universe. Sure, the science of astronomy was thousands of years old, and the telescope itself had been around for the better part of three centuries. We had measured stars, comets, asteroids, and nebulae; we had witnessed novae and supernovae; we had discovered variable stars and knew about atoms; and we had revealed intriguing structures in the sky, like spirals and ellipticals.

But we didn’t know that these spirals and ellipticals were galaxies all unto themselves. In fact, that was only the second-most popular idea; the leading idea of the day was that they were entities — perhaps proto-stars in the process of forming — contained within the Milky Way, which itself comprised the entire Universe. Einstein was looking for a theory of gravity that could be applied to anything and everything that existed, and that included the known Universe as a whole.

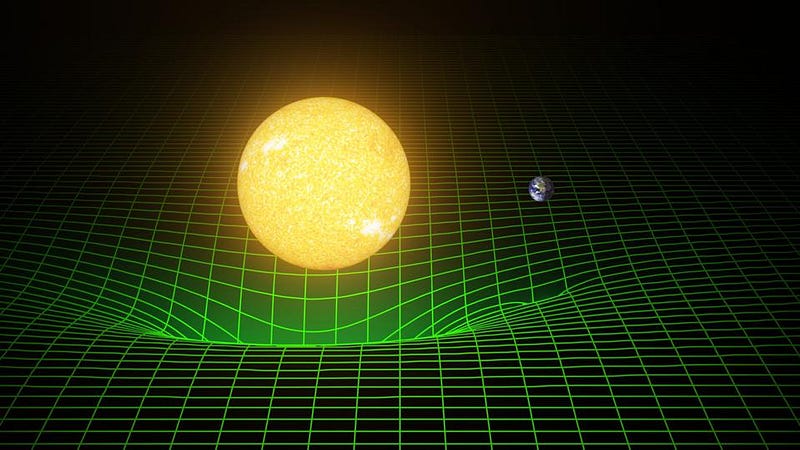
The problem became apparent when Einstein succeeded in formulating his theoretical crown jewel: General Relativity. Instead of being based on masses exerting forces on one another infinitely fast across infinite distances, Einstein’s conception was vastly different. First, because space and time were relative for each and every observer, not absolute, the theory needed to give identical predictions for all observers: what physicists call “relativistically invariant.” That meant instead of separate notions of space and time, they needed to be woven together into a four-dimensional fabric: spacetime. And instead of propagating at infinite speeds, gravitational effects were limited by the speed of gravity, which — in Einstein’s theory — equals the speed of light.

The key advance that Einstein made was that, instead of masses pulling on each other, gravity worked by both matter and energy curving the fabric of spacetime. That curved spacetime, in turn, then dictated how matter and energy moved through it. At each instant in time, the matter and energy in the Universe tells spacetime how to curve, the curved spacetime tells matter how to move, and then it does: the matter and energy moves a tiny bit and the spacetime curvature changes. And then, when the next instant arrives, the same equations of General Relativity tell both the matter and energy and the spacetime curvature how to evolve into the future.

If Einstein had stopped there, he would have instigated a cosmic revolution. On the one hand (and hence, on one side of the equation), you had all the matter and energy in the Universe, while on the other hand (and the other side of the equals sign in the equation), you had the curvature of spacetime. That should be it, of course; whatever the equations predict should tell you what happens next.

When Einstein solved those equations a large distance away from a small mass, he got Newton’s law of universal gravitation back. When he got closer to the mass, he started to get corrections, which both explained the (hitherto inexplicable) orbit of Mercury and predicted that starlight passing near the Sun during a total solar eclipse would be deflected. This, after all, was how General Relativity was first validated when put to the test.

But there was another problem that arose in a different situation. If we assumed that the Universe was filled roughly evenly with matter, we could solve that scenario. What Einstein discovered was disconcerting: the Universe was unstable. If it began in a stationary spacetime, the Universe would collapse in on itself. So Einstein, to fix this, invented a cosmological constant.

You have to understand where the idea of a cosmological constant comes from. There’s a very powerful mathematical tool that we use all the time in physics: a differential equation. Don’t be scared by the big words; something as simple as Newton’s F = ma is a differential equation. All it means is that this equation tells you how something will behave in the next moment, and then, once that moment has elapsed, you can put those new figures back into the same equation, and it will go on to tell you what happens in the next moment.

A differential equation, for instance, will tell you what happens to a ball rolling down a hill on the Earth. It tells you what path it will take, how it will accelerate, and how its position will change at every moment in time. Just by solving the differential equation describing the ball rolling down the hill, you can know precisely what trajectory it will take.

The differential equation tells you almost everything you’d want to know about the ball rolling down the hill, but there’s one thing it can’t tell you: how high the base level of the ground is. You have no way of knowing whether you’re on a hill atop a plateau, on a hill that ends at sea level, or on a hill that ends in a hollowed-out volcanic crater. An identical hill at all three elevations will be described by the exact same differential equation.

That same problem shows up in calculus when you first learn how to do an indefinite integral; anyone who’s taken calculus will remember the infamous “plus C” that you have to add at the end. Well, Einstein’s General Relativity isn’t just one differential equation, but a matrix of 16 differential equations, related in such a way that 10 of them are independent of one another. But to each of those differential equations, you can add a constant in a particular way: what became known as the cosmological constant. Perhaps surprisingly, it’s the only thing you can add to General Relativity — besides another form of matter or energy — that won’t fundamentally alter the nature of Einstein’s theory.

Einstein put a cosmological constant into his theory not because it was allowed, but because, for him, it was preferred. Without adding a cosmological constant in, his equations predicted that the Universe should either be expanding or contracting, something that clearly wasn’t happening. Instead of going with what the equations said anyway, Einstein threw the cosmological constant in there in order to “fix” what appeared to be an otherwise broken situation. If he had listened to the equations, he could have predicted the expanding Universe. Instead, the work of others would have to overturn Einstein’s prejudicial choices, with Einstein himself only abandoning the cosmological constant in the 1930s, well after the expanding Universe had been observationally established.

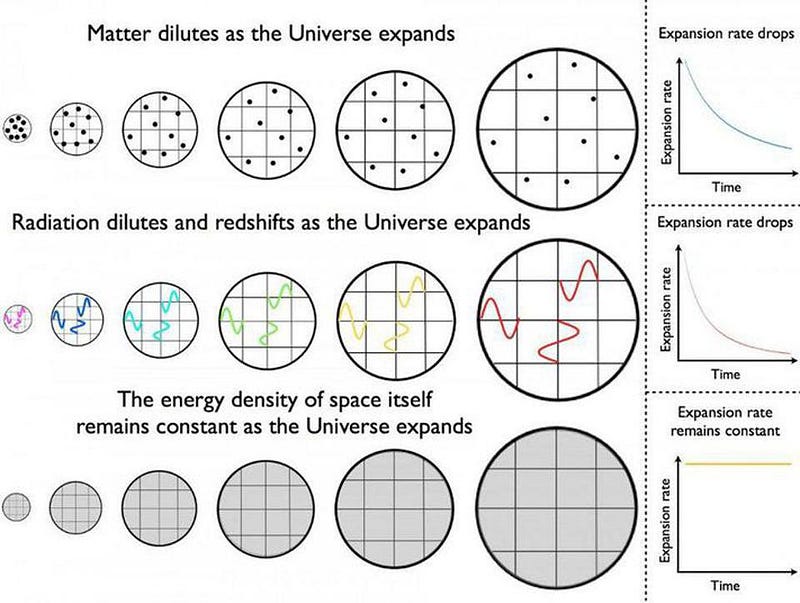
The thing is, the cosmological constant is unlike the types of energy we know of otherwise. When you have matter in the Universe, you have a fixed number of particles. As the Universe expands, the number of particles stays the same, so the density goes down over time. With radiation, not only are the number of particles fixed, but as the radiation travels through the expanding Universe, its wavelength stretches relative to an observer that will someday receive it: its density goes down, and each individual quantum also loses energy with time.

But for a cosmological constant, it’s a constant form of energy that’s intrinsic to space. It’s would be like if the surface of the Earth weren’t at sea level, but instead were raised up by an extra few dozen feet or so. Yes, you could just call that new height “sea level” (and in fact, we would do that if we still had seawater here on Earth), but for the Universe, we can’t. There’s no way to “know” what the value of the cosmological constant is; we’ve simply assumed that it would be zero. But it doesn’t have to be; it could take on any value at all: positive, negative, or zero.

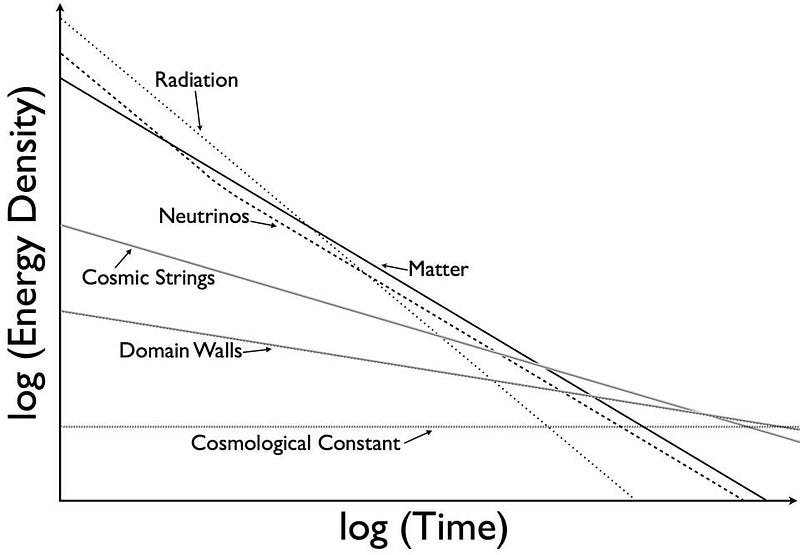
If we extrapolate back in time — to when the Universe was younger, hotter, denser, and smaller — the cosmological constant wouldn’t have been noticeable. It would have been swamped by the much larger effects of matter and radiation early on. Only after the Universe has expanded and cooled so that the matter and radiation density drops to a low enough value can the cosmological constant finally appear.

That is, if there’s a cosmological constant at all.

When we talk about dark energy, it might turn out to be a cosmological constant. Certainly, when we take all of the observations we have so far, it appears that dark energy is consistent with being a cosmological constant, as the way the expansion rate changes over time agrees, within the uncertainties, with what a cosmological constant would be responsible for. But there are uncertainties there, and dark energy could be:

• increasing or decreasing in strength over time,
• changing in energy density, unlike a cosmological constant,
• or evolving in a novel, complicated fashion.

Although we have constraints on how much dark energy could be evolving by over the past ~6 billion years or so, we cannot definitively say it’s a constant.

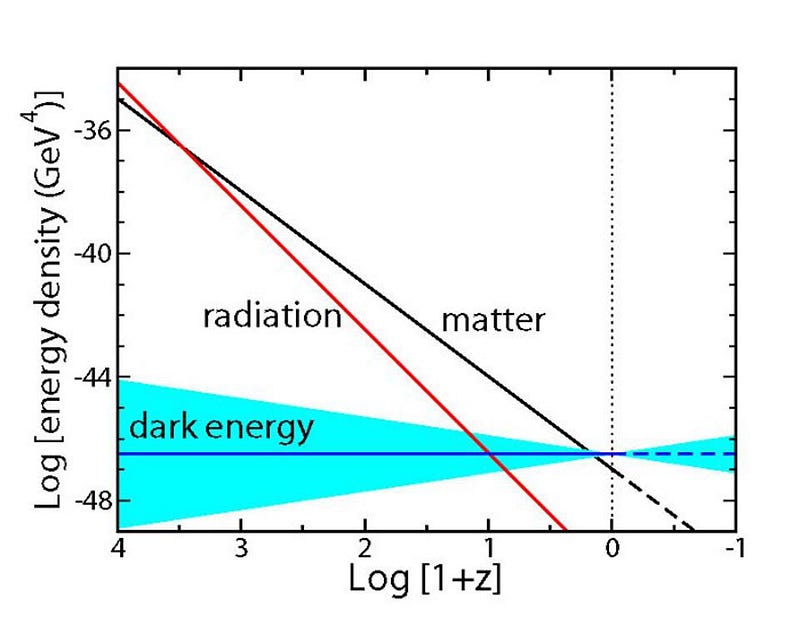
We would like to know, of course, whether it is a constant or not. The way we’re going to make this determination, as is always the case in science, is with superior and subsequent observations. Large data sets are the key, as is sampling the Universe at a wide variety of distances, as it’s the way the light evolves as it travels through the expanding Universe that allows us to determine — in gory detail — how the expansion rate has changed over time. If it’s exactly equal to a cosmological constant, there’s a particular curve it’ll follow; if not, it’ll follow a different curve, and we’ll be able to see that.

By the end of the 2020s, we’ll have an enormous and comprehensive ground-based survey of the Universe thanks to the Vera C. Rubin observatory, which will supersede everything that surveys like Pan-STARRS and the Sloan Digital Sky Survey have done. We’ll have an enormous suite of space-based data thanks to the ESA’s Euclid observatory and NASA’s Nancy Roman telescope, which will see more than 50 times as much Universe as Hubble presently sees. With all of this novel data, we should be able to determine whether dark energy, which is a general term for any novel form of energy in the Universe, is truly identical to what the very specific “cosmological constant” predicts, or whether it varies in any way at all.

It’s extremely tempting — and I’ll confess, I sometimes do it myself — to simply conflate the two, and assume that dark energy is nothing more complex than a cosmological constant. It’s understandable why we’d do this: the cosmological constant is already allowed as part of General Relativity without additional explanation. Furthermore, we don’t know how to calculate the zero-point energy of empty space in quantum field theory, and that contributes to the Universe in exactly the same fashion as a cosmological constant would as well. Finally, when we make our observations, they’re all consistent with dark energy being a cosmological constant, with no need for anything more complicated.

But that underscores exactly why it’s so vitally important to make these novel measurements. If we didn’t bother to measure the Universe in a careful, precise, intricate fashion, we’d never have discovered the need for Einstein’s relativity in the first place. We never would have discovered quantum physics, nor would we have conducted most of the Nobel-winning research that’s driven society forward over the 20th and 21st centuries. 10 years from now, we’ll have the data to know whether dark energy differs from a cosmological constant by as little as 1%.

The cosmological constant may be the same thing as dark energy, but it doesn’t need to be. Even if it is, we’d still like to understand why it behaves this particular way and not any other. As 2020 comes to a close and 2021 dawns, it’s important to remember the most vital lesson of all: the answers to our deepest cosmic questions are written on the face of the Universe. If we want to know them, the only way is to put the question to our physical reality itself.

Send in your Ask Ethan questions to startswithabang at gmail dot com!

Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.