LIGO successfully squeezes quantum states, surpassing Heisenberg’s limits

- In the quest to detect the ripples in spacetime produced by all gravitational wave sources, achieving maximum sensitivity is of paramount importance.
- There are typically limits to how sensitive an experiment can probe, determined practically by various sources of noise but also, theoretically, by the inherent quantum rules that govern reality.
- By taking advantage of an esoteric phenomenon known as “quantum squeezing,” the LIGO collaboration has surpassed the traditional quantum limit in their search for the smallest signals of all. Gravitational wave detection just received an incredible boost as a result.
In the quest to detect gravitational waves, there are a number of obstacles that — no matter how hard we try — continue to stand in our way. Since 2015, with the advent of first the advanced LIGO detectors and then later, the Virgo detector, humanity has directly detected gravitational waves from a particular set of sources: merging stellar-mass black holes, merging neutron stars, and (perhaps) merging black hole-neutron star pairs. More recently, a different technique, leveraging pulsar timing, has discovered a cosmic “hum,” or the sum of all background gravitational wave signals with a much longer timing period.
Nevertheless, there are still limits to what we can do with current technology.
- We’re frequency-limited, meaning that we can only detect sources from systems that strongly emit gravitational waves with a specific, narrow range of orbital periods. (This is why LIGO is only sensitive to relatively low-mass sources.)
- We’re limited by the seismic noise floor of Earth, as subterranean vibrations, even due to the subtle phenomenon of plate tectonics, prevents terrestrial detectors from seeing signals below a certain (strain) amplitude.
- And we’re limited by the laws of physics themselves, which prevent us from knowing all properties of any signal simultaneously, even within our own detectors.
While much of the attention on gravitational wave detection has focused on getting as close to the theoretical noise floor of our detectors as possible, a remarkable advance has just occurred on that last front: surpassing the standard quantum limit for signals in our detectors. Here’s the science behind how it was done.

There are two main aspects to understand as background for this achievement. The first is how gravitational wave detectors like LIGO and Virgo work here on Earth’s surface, and the second is an understanding of what the quantum limit normally is, and how it plays a role within our gravitational wave observatories.
How gravitational wave detectors work
The technology at the heart of our ground-based gravitational wave detectors is actually remarkably old, and goes all the way back to the 19th century: interferometry. In an interferometer, what you normally do is:
- take an initial source of light,
- split it into two perpendicular components,
- send one component down a specific distance away in one direction, while the other component goes down that same specific distance in a perpendicular direction,
- then reflect those signals off of mirrors at the far end,
- bring the two components of the signal back together,
- and observe them, at the end, in your detector.
This was famously leveraged in the 1880s by the duo of A.A. Michelson and E.W. Morley, who expected that they’d be able to detect the long-sought-after aether by performing the experiment. The rationale is that, since Earth moves through space (around the Sun) at 30 km/s, and the speed of light is only about 10,000 times that, at 300,000 km/s, then a sensitive enough interferometer will reveal Earth’s true motion relative to whatever medium it is that light travels through.

This experimental idea, as brilliant as it was, was not successful, as it (and many successive improvements to it) yielded only null results. It turned out that there’s no such thing as an aether, and the reason Michelson and Morley’s experiment didn’t display a signal is because the speed of light is identical for all observers in all reference frames; there is no “slowing” of light in the direction of Earth’s motion at all. This wasn’t explained successfully until 1905, however, when Einstein put forth his special theory of relativity. The Michelson-Morley experiment was such an important aspect of this discovery that Michelson, alone, was awarded the 1907 Nobel Prize in physics.
However, this same interferometry technique would prove incredibly useful more than 100 years later, as scientists began designing and building the apparatuses needed to directly detect gravitational waves. With a constant speed of light to all observers, the one way an interferometer-like setup could still give a signal would be if the length of the two perpendicular “arms” changed relative to one another. This is precisely what’s predicted to happen when a gravitational wave passes through one of these detectors, as they cause space to alternately contract-and-expand in mutually perpendicular directions.

If the speed of light is constant, then seeing a shift in the arrival time of the two different pulses — or a corresponding shift in the phase of the reconstructed interference pattern — would correspond to changes in the arm-length within your gravitational wave detectors. Since the cosmic mergers that create gravitational waves produce precisely this type of alternating contraction-and-expansion effects in mutually perpendicular directions, augmented by the technique of reflecting the laser light within your cavity a few thousand times before recombining the beams and reconstructing your signal, observing a periodic shift in your observed interference pattern should reveal the presence of gravitational waves.
This was precisely the method used by the LIGO and Virgo teams to successfully detect gravitational waves: something that’s been done in excess of 100 times so far. While LIGO and Virgo are limited to seeing stellar mass black holes (of about 300 solar masses or fewer) and neutron stars merge with one another, owing to the brief periods of those objects relative to the more massive ones which also generate gravitational wave signals, their successes have paved the way for future gravitational wave detectors that will be sensitive to longer periods, both here on Earth as well as in space in the near future.

Understanding the quantum limit
Of course, as with any quantum measurement, it’s impossible to measure what are known as complementary quantities to arbitrary precision at the same time. Known most famously from the example of the Heisenberg uncertainty principle, the quantum nature of reality ensures that, for certain pairs of properties, the better you measure (or come to know) one aspect of reality, the greater the induced uncertainty becomes in what’s known as its “complementary” quantity. For example:
- If you measure the position of an object more and more precisely, the momentum of that object becomes more inherently uncertain, and vice versa.
- If you measure the lifetime of an unstable particle more and more precisely, the energy (including even the rest-mass energy) of that particle becomes more inherently uncertain, and vice versa.
- If you measure the orientation of a particle, its angular momentum becomes more uncertain, and vice versa.
- If you measure a particle’s inherent spin in one direction, its inherent spin in the two other mutually perpendicular directions becomes more uncertain, and vice versa.
Many other examples also exist: voltage and free electric charge, electric field and electric polarization density, magnetic vector potential and the density of free electric current, and so on. Although the “position-momentum” uncertainty relation is by far the most famous one, it’s just one of many examples of quantum uncertainty.
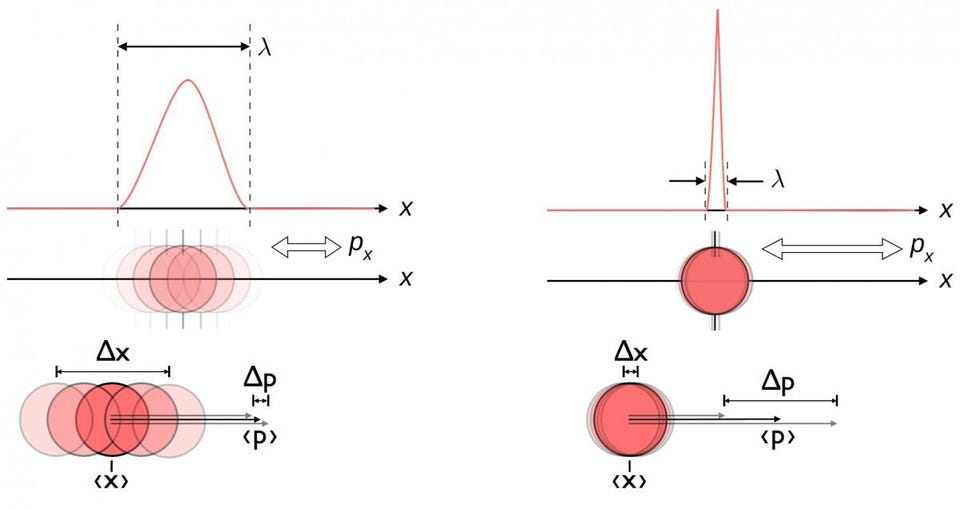
What’s much less well-appreciated than these conventional uncertainty relations is one that’s very important to the LIGO detector, because it’s relevant to the photons that travel down-and-back, over and over, across their interferometer arms: the uncertainty relation between the amplitude and phase of a light signal. An interesting analogy — particularly relevant in the post-COVID era — is when you conduct a video call with another person, given limited total bandwidth. With only so much total data that can fit down the pipeline, there’s a trade-off that must be made, but it’s a trade-off that allows you to choose between:
- whether you want both middling-quality audio and video,
- whether you want high-quality audio at the expense of having worse-quality video,
- or whether you want good-quality video at the expense of having interrupted, irregular audio.
Similarly, with the amplitude and phase of a signal, there’s a total amount of “inherent uncertainty” that cannot be removed from both of these signal components, combined, no matter what physical trick you use. But through the technique of squeezed quantum states, you can trade-off how much uncertainty you allow in each of “amplitude” and “phase” accuracy, individually, to extract the maximal possible signal from your data in the effort to detect gravitational waves.
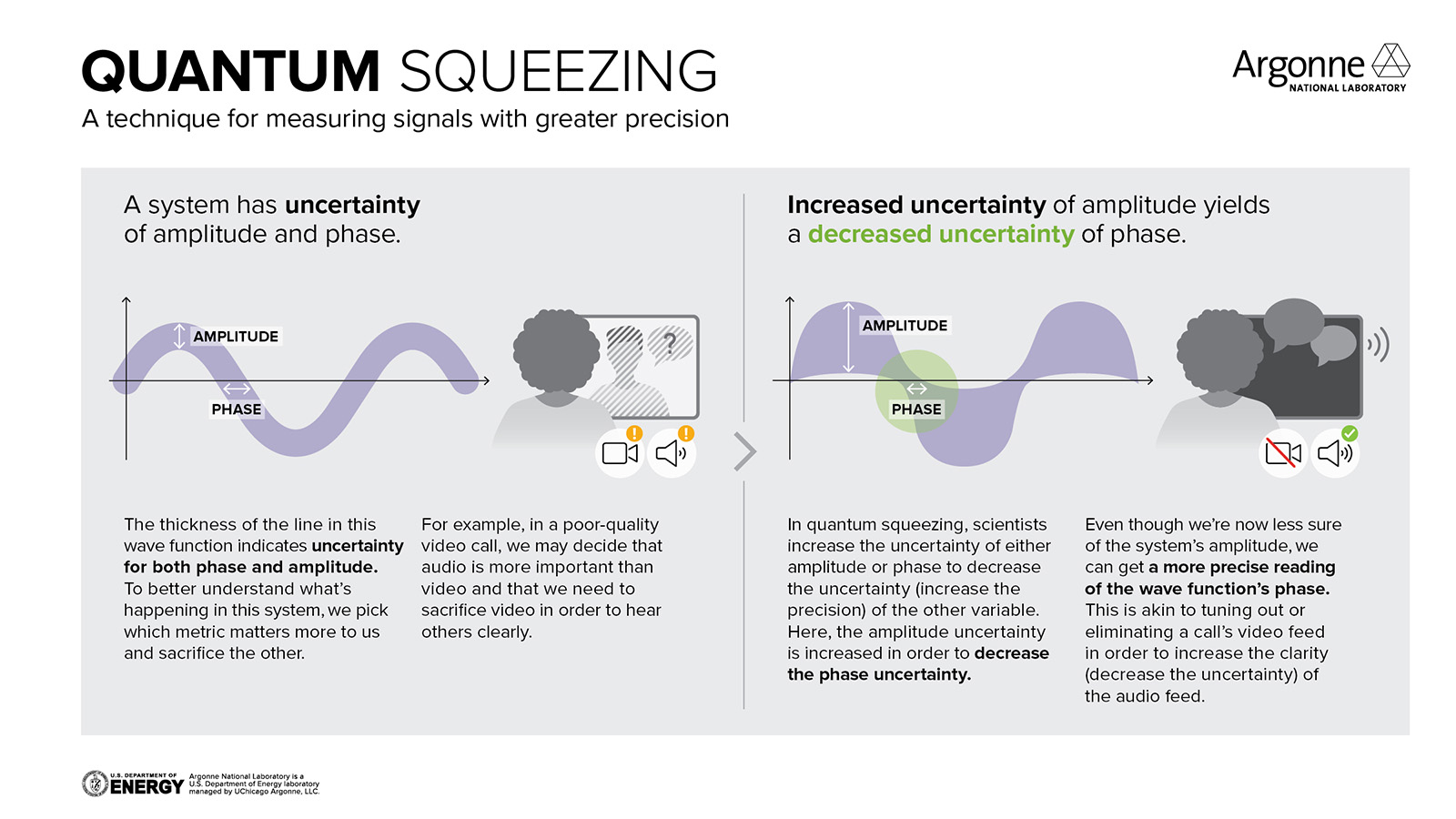
Surpassing Heisenberg’s default limits
Instead of allowing nature to make the choice (i.e., the “default” choice of your equipment), the researchers who design and work with the optical systems at the heart of LIGO — producing laser pulses, bouncing them off of mirrors, and recombining them to create an interference pattern — have begun optimizing this trade-off to maximize the amount of information that can be extracted from a gravitational wave signal. Through an even greater effort, the LIGO facilities have now leveraged what’s known as frequency-dependent quantum squeezing, where a greater amplitude uncertainty is chosen at later times in the merger and a greater phase uncertainty is chosen at earlier times in the merger, to improve upon the “default” sensitivity that was previously achieved with nature making that decision.
The result, remarkably, is that LIGO’s detection sensitivity has now improved, owing solely to the advances in quantum squeezing, by up to a whopping 65%: enabling us to detect mergers at greater distances than would otherwise be possible as well as seeing and characterizing fainter-amplitude (e.g., lower-mass or greater-radius) signals than would otherwise be possible. Additionally, this improvement should enable better source characterization, helping scientists pin down properties (like mass and distance) for any mergers observed.
One of the challenges for this technique is that the mirrors that reflect LIGO’s laser light are, themselves, a source of quantum noise: even at cryogenic temperatures and with the most pristine vacuum inside the laser arms ever created on Earth. At high frequencies, knowing the amplitude of the signal is less important, as it’s the knowledge of the phases (i.e., the arrival time of the light in the two arms relative to one another) that helps improve LIGO’s sensitivity. However, “squeezing” the most out of your phases at high frequencies causes the mirrors themselves to vibrate back-and-forth: a phenomenon known as “rumble” within LIGO’s mirrors.
At lower frequencies, however, the light can be squeezed in a different fashion: to optimize the amplitude of the wave (reducing this “rumble”) at the expense of a less-well-known phase, which is okay and preferred, because the low-frequency phase characterization of these sources is less important than the high-frequency’s phase signals are for teaching us about the properties of these sources. However, optimizing the amplitude at low-frequencies helps us identify the signal earlier than ever, which gives us more data to work with, period. A video explaining LIGO’s frequency-dependent quantum squeezing is included here to help further illustrate what’s going on.
Since 2019, LIGO has leveraged the technique of quantum squeezing by applying it to the light traveling in their cavities, but weren’t able to control this “squeezing” in a frequency-dependent way. You’re going to have quantum noise in the phase (or frequency) of your laser light, which affects how well you can measure the timing of the gravitational wave signals that LIGO is sensitive to. Similarly, you’re going to also have quantum noise in the amplitude (or power) of the laser light, with greater amplitude uncertainties affecting the motion of your mirrors, which specifically limit LIGO’s sensitivity to low-frequency gravitational waves.
By developing and implementing a new frequency-dependent squeezing cavity, LIGO now enjoys the best-of-both-worlds: where the high frequencies have greater phase sensitivity and the low frequencies have greater amplitude sensitivity. As Professor Rana Adhikari of Caltech put it:
“Before, we had to choose where we wanted LIGO to be more precise. Now we can eat our cake and have it too. We’ve known for a while how to write down the equations to make this work, but it was not clear that we could actually make it work until now. It’s like science fiction.”

Even though LIGO isn’t just a macroscopic endeavor, but a huge one — after all, its dual laser arms are 4 kilometers long apiece — the nature of how it works ensures that even tiny quantum effects are important as far as its precise capabilities are concerned. Although LIGO began squeezing light for its third (O3) data run in 2019 and 2020, it was closed down for upgrades prior to its newest observing run. Starting back up for its fourth (O4) run in May of 2023 with these new frequency-dependent cavities for squeezing light, LIGO’s twin detectors will run until early 2025, and will be joined by an upgraded Virgo detector (also leveraging squeezed light) in just a few months.
You might not think of quantum uncertainty as a fundamental limitation when it comes to the science of astronomy, but in the realm of gravitational waves, our detectors are so precise that every minuscule improvement can translate into a powerful enhancement when it comes to exploring the distant and faint Universe. As MIT’s Lisa Barsotti put it:
“We can’t control nature, but we can control our detectors… The quantum nature of the light creates the problem, but quantum physics also gives us the solution.”
Joining LIGO and Virgo in the hunt for gravitational waves, the KAGRA gravitational wave observatory adds a fourth detector to the mix, and like Virgo, will soon leverage frequency-dependent quantum squeezing as well. The net result will be a clearer window into the gravitational wave Universe than ever before.