Wolfgang Pauli’s quantum rule makes existence possible

- When it comes to the foundation of quantum physics, ideas like energy quantization, wave/particle duality, and the uncertainty principle always loom large in people’s minds.
- But the Pauli Exclusion Principle, stating that two identical particles of one (fermionic, not bosonic) type can’t occupy identical quantum states, is much less appreciated.
- Without it, however, existence as we know it, including Earth and everything on it, simply wouldn’t be interesting at all.
Take a look around you at everything on Earth. If you were to investigate what any object is made out of, you could subdivide it into progressively smaller and smaller chunks. All living creatures are made up of cells, which in turn are composed of a complex array of molecules, which themselves are stitched together out of atoms. Atoms themselves can be broken down further: into atomic nuclei and electrons. And finally, atomic nuclei can be further decomposed into their constituent fundamental particles: quarks and gluons. At an elementary level, these are the constituent components of all matter on Earth and, for that matter, all the normal matter we know of in the Universe.
But how do these relatively simple component particles come to make up everything that we see, know, and interact with, here on Earth and in the Universe beyond our world? Even the simplest of complex structures, the atoms, which are composed of atomic nuclei and electrons, come in less than 100 stable or quasi-stable varieties. How is it that such a simple set of “building blocks” gives rise to the enormous diversity of molecules, objects, creatures and everything else we find?
The answer comes down to one underappreciated quantum rule: the Pauli Exclusion Principle.
When most of us think of quantum mechanics, we think of the bizarre and counterintuitive features of our Universe on the smallest scales. We think about Heisenberg uncertainty, and the fact that it’s impossible to simultaneously know pairs of physical properties (like position and momentum, energy and time, or angular momentum in two perpendicular directions) beyond a limited mutual precision.
We think about the wave-particle nature of matter, and how even single particles (like electrons or photons) can behave as though they interfere with themselves. And we often think about Schrödinger’s cat, and how quantum systems can exist in a combination of multiple possible outcomes simultaneously, only to reduce to one specific outcome when we make a critical, decisive measurement.

Most of us barely give a second thought to the Pauli Exclusion Principle, which simply states that no two identical fermions can occupy the same exact quantum state in the same system.
Big deal, right?
Actually, it’s not only a big deal; it’s the biggest deal of all. When Niels Bohr first put out his model of the atom, it was simple but extremely effective. By viewing the electrons as planet-like entities that orbited the nucleus, but only at explicit energy levels that were governed by straightforward mathematical rules, his model reproduced the coarse structure of matter. As electrons transitioned between the energy levels, they emitted or absorbed photons, which in turn described the spectrum of each individual element.
But Bohr’s model was just that: a model that successfully described what was seen. What it didn’t do was explain why this set of rules would exist at all, or provide a set of axioms that allowed such rules to be derived.

That’s where the Pauli Exclusion Principle comes in. Simply by demanding that no two identical fermions in the same quantum system occupy the same quantum state, this complex structure emerges: for the behavior of electrons within atoms, as well as for all other composite systems containing multiple identical fermions.
If it weren’t for the Pauli Exclusion Principle, the matter we have in our Universe would behave in an extraordinarily different fashion. The electrons, you see, are examples of fermions. Every electron is fundamentally identical to every other electron in the Universe, with the same charge, mass, lepton number, lepton family number, and intrinsic angular momentum (or spin).
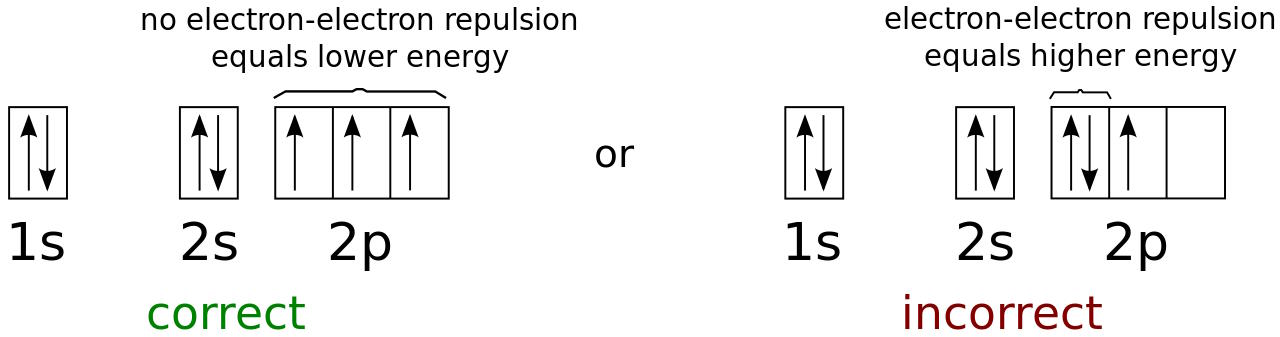
If there were no Pauli Exclusion Principle, there would be no limit to the number of electrons that could fill the ground (lowest-energy) state of an atom. Over time, and at cool enough temperatures, that’s the state that every single electron in the Universe would eventually sink to. The lowest energy orbital — the 1s orbital in each atom — would be the only orbital to contain electrons, and it would contain all of the electrons inherent to every atom.

Of course, this is not the way our Universe works, and that’s an extremely good thing. Electrons occupy different energy levels within an atom, and once an energy level becomes “filled,” the electrons must resign themselves to occupying the next available level. The Pauli Exclusion Principle is exactly what prevents all the electrons from falling into the same lowest-energy (ground) state by that one simple rule: you cannot put more than one identical fermion in the same quantum state.
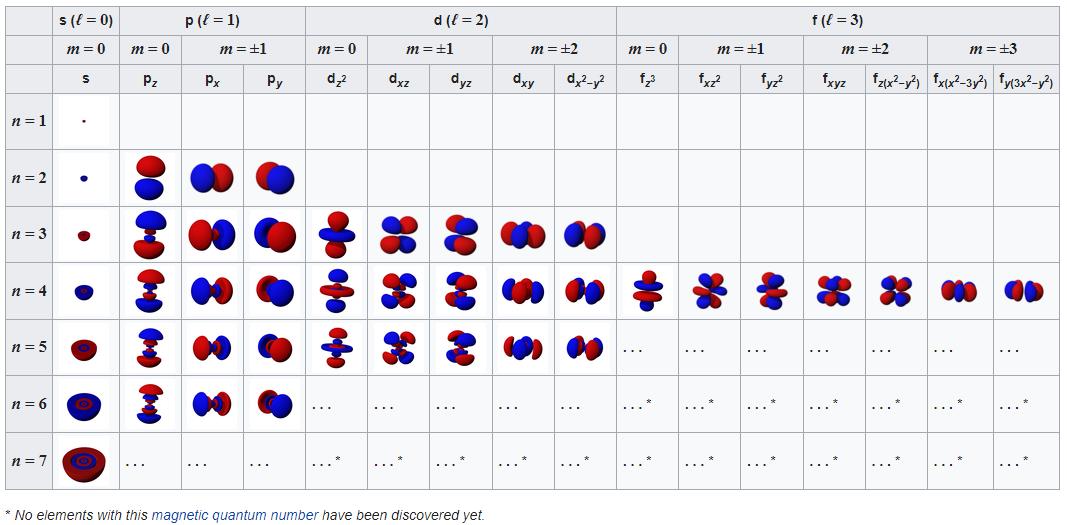
Sure, the first electron can slide into the lowest-energy state: the 1s orbital. If you take a second electron and try to put it in there, however, it cannot have the same quantum numbers as the previous electron. Electrons, in addition to the quantum properties inherent to themselves (like mass, charge, lepton number, etc.) also have quantum properties that are specific to the bound state they’re in. When they’re bound to an atomic nucleus, that includes energy level, angular momentum, magnetic quantum number, and spin quantum number.
The lowest-energy electron in an atom will occupy the lowest (n = 1) energy level, and will have no angular momentum (l = 0) and therefore a magnetic quantum number of 0 as well. The electron’s spin, though, offers a second possibility. Every electron has a spin of ½, and so will the electron in the lowest-energy (1s) state in an atom.
When you add a second electron, it can have the same spin but be oriented in the opposite direction, for an effective spin of -½. This way, you can fit two electrons into the 1s orbital. After that, it’s full, and you have to go to the next energy level (n = 2) to start adding a third electron. The 2s orbital (where l = 0, also) can hold an additional two electrons, and then you have to go to the 2p orbital, where l = 1, and you can have three magnetic quantum numbers: -1, 0, or +1, and each of those can hold electrons with spin of +½ or -½.
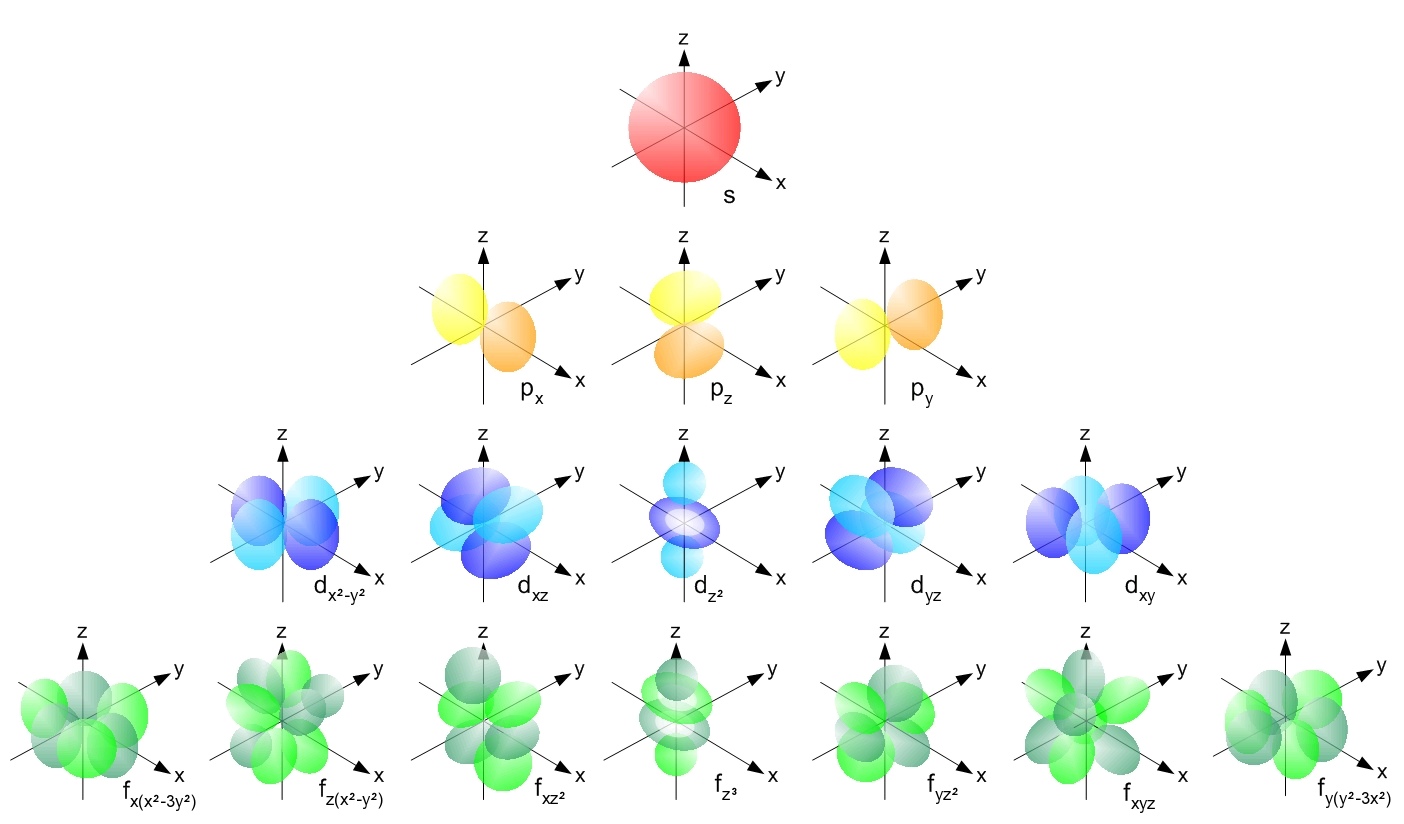
The Pauli Exclusion Principle — and the fact that we have the quantum numbers that we do in the Universe — is what gives each individual atom their own unique structure. As we add greater numbers of electrons to our atoms, we have to go to higher energy levels, greater angular momenta, and increasingly more complex orbitals to find homes for all of them. The energy levels work as follows:
- The lowest (n = 1) energy level has an s-orbital only, as it has no angular momentum (l = 0) and can hold just two (spin +½ and -½) electrons.
- The second (n = 2) energy level has s-orbitals and p-orbitals, as it can have an angular momentum of 0 (l = 0) or 1 (l = 1), which means you can have the 2s orbital (where you have spin +½ and -½ electrons) holding two electrons and the 2p orbital (with magnetic numbers -1, 0, and +1, each of which holds spin +½ and -½ electrons) holding six electrons.
- The third (n = 3) energy level has s, p, and d-orbitals, where the d-orbital has an angular momentum of 2 (l = 2), and therefore can have five possibilities for magnetic numbers (-2, -1, 0, +1, +2), and can therefore hold a total of ten electrons, in addition to the 3s (which holds two electrons) and 3p (which holds six electrons) orbitals.
Each individual atom on the periodic table, under this vital quantum rule, will have a different electron configuration than every other element. Because it’s the properties of the electrons in the outermost shells that determine the physical and chemical properties of the element it’s a part of, each individual atom has its own unique sets of atomic, ionic, and molecular bonds that it’s capable of forming.
No two elements, no matter how similar, will be the same in terms of the structures they form. This is the root of why we have so many possibilities for how many different types of molecules and complex structures that we can form with just a few simple raw ingredients. Each new electron that we add has to have different quantum numbers than all the electrons before it, which alters how that atom will interact with everything else.

The net result is that each individual atom offers a myriad of possibilities when combining with any other atom to form a chemical or biological compound. There is no limit to the possible combinations that atoms can come together in; while certain configurations are certainly more energetically favorable than others, a variety of energy conditions exist in nature, paving the way to form compounds that even the cleverest of humans would have difficulty imagining.
But the only reason that atoms behave this way, and that there are so many wondrous compounds that we can form by combining them, is that we cannot put an arbitrary number of electrons into the same quantum state. Electrons are fermions, and Pauli’s underappreciated quantum rule prevents any two identical fermions from having the same exact quantum numbers.

If we didn’t have the Pauli Exclusion Principle to prevent multiple fermions from having the same quantum state, our Universe would be extremely different. Every atom would have almost identical properties to hydrogen, making the possible structures we could form extremely simplistic. White dwarf stars and neutron stars, held up in our Universe by the degeneracy pressure provided by the Pauli Exclusion Principle, would collapse into black holes. And, most horrifically, carbon-based organic compounds — the building blocks of all life as we know it — would be an impossibility for us.
The Pauli Exclusion Principle isn’t the first thing we think of when we think of the quantum rules that govern reality, but it should be. Without quantum uncertainty or wave-particle duality, our Universe would be different, but life could still exist. Without Pauli’s vital rule, however, hydrogen-like bonds would be as complex as anything in the Universe ever got, leading to a simple, boring Universe with no possibility for complex molecules, complex chemical reactions, or life.





