Spacetime: is it real and physical, or just a calculational tool?

- In order for something to be physically real, it needs to be physical and measurable directly, not just a calculational tool that makes correct predictions.
- In this sense, atoms and observable particles are definitely real, but unobservable “virtual” particles are definitely not.
- What about spacetime? Is it real like atoms are, or just a calculational tool? It’s a fascinating topic to explore.
When most of us think about the Universe, we think about the material objects that are out there across the great cosmic distances. Matter collapses under its own gravity to form cosmic structures like galaxies, while gas clouds contract to form stars and planets. Stars then emit light by burning their fuel through nuclear fusion, and then that light travels throughout the Universe, illuminating anything it comes into contact with. But there’s more to the Universe than the objects within it. There’s also the fabric of spacetime, which has its own set of rules that it plays by: General Relativity. The fabric of spacetime is curved by the presence of matter and energy, and curved spacetime itself tells matter and energy how to move through it.
But what, exactly, is the physical nature of spacetime? Is it a real, physical thing, like atoms are, or is it merely a calculational tool that we use to give the right answers for the motion and behavior of the matter within the Universe?
It’s an excellent question and a tough one to wrap your head around. Moreover, before Einstein came along, our conception of the Universe was very different from the one we have today. Let’s go way back to the Universe before we even had the concept of spacetime, and then come forward to where we are today.
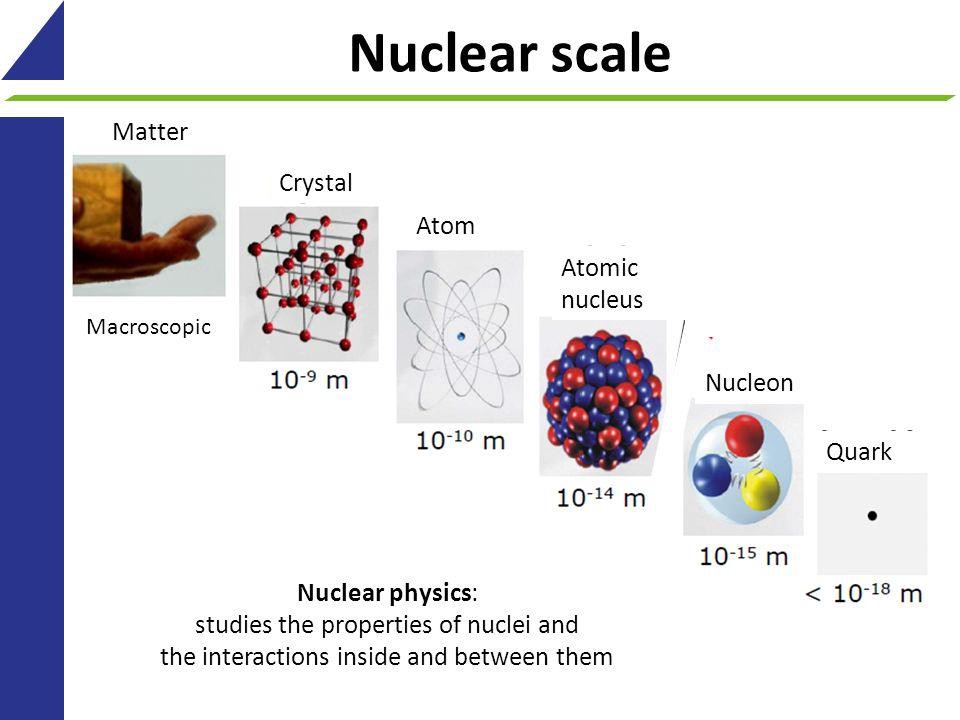
At a fundamental level, we had long supposed that if you took everything that was in the Universe and cut it up into smaller and smaller constituents, you’d eventually reach something that was indivisible. Quite literally, that’s what the word “atom” means: from the Greek ἄτομος: not able to be cut. The first record we have of this idea goes back some 2400 years to Democritus of Abdera, but it’s plausible that it may go back even farther. These “uncuttable” entities do exist; each one is known as a quantum particle. Despite the fact that we took the name “atom” for the elements of the periodic table, it’s actually subatomic particles like quarks, gluons, and electrons (as well as particles that aren’t found in atoms at all) that are truly indivisible.
These quanta bind together to build up all the complex structures we know of in the Universe, from protons to atoms to molecules to human beings. And yet, no matter what types of quanta we deal with — matter or antimatter, massive or massless, fundamental or composite structures, on subatomic or cosmic scales — those quanta only exist within the same Universe that we do.

This is important, because if you want the “stuff” in your Universe to do things to one another — interact, bind together, form structures, transfer energy, etc. — there has to be a way for the different things that exist within the Universe to affect one another. It’s similar to having a play where you have all the characters fleshed out, all the actors ready to play them, all the costumes ready to be worn, and all the lines written and memorized. The only thing missing, and yet very necessary for the play to occur, is a stage.
What is that stage, then, in physics?
Before Einstein came along, the stage was set by Newton. All of the “actors” in the Universe could be described by a set of coordinates: a location in three-dimensional space (a position) as well as a moment in time (an instant). You can envision it like a Cartesian grid: a three-dimensional structure with an x, y, and z axis, where every quantum can also have a momentum, describing its motion through space as a function of time. Time itself was assumed to be linear, always passing at the same rate. In Newton’s picture, both space and time were absolute.

However, the discovery of radioactivity in the late 19th century began to throw Newton’s picture into doubt. The fact that atoms could emit subatomic particles moving close to the speed of light taught us something exciting: when a particle moved close to the speed of light, it experienced space and time very differently from something that was either slow-moving or at rest.
Unstable particles that would decay very quickly at rest lived longer the closer to the speed of light they moved. Those same particles traveled greater distances than their speeds and lifetimes would indicate before decaying. And if you tried to calculate the energy or momentum of a particle in motion, different observers (i.e., people watching the particle and moving at different speeds relative to it) would calculate values that were inconsistent with one another.
Something must be flawed with Newton’s conception of space and time. At speeds close to the speed of light, time dilates, lengths contract, and energy and momentum really are frame-dependent. In short, the way you experience the Universe depends on your motion through it.

Einstein was responsible for the remarkable breakthrough of the concept of relativity, which identified which quantities were invariant and didn’t change with the observer’s motion, and which ones were frame-dependent. The speed of light, for example, is the same for all observers, as is the rest mass of any quantum of matter. But the spatial distance you’d perceive between two points depended very strongly on your motion along the direction connecting those points. Similarly, the rate at which your clock ran as you journeyed from one point to another also depended on your motion.
Space and time weren’t absolute, as Newton intuited, but were experienced differently by different observers: they were relative, which is where the name “relativity” comes from. Moreover, there was a specific relationship between how any particular observer experienced space and how they experienced time: something that was put together a couple of years after Einstein put forth his special theory of relativity by his former professor, Hermann Minkowski, who laid out a unified mathematical structure encompassing space and time together: spacetime. As Minkowski himself put it,
“Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”
Today, this spacetime is still commonly used as our stage whenever we neglect gravity: Minkowski space.

But in our real Universe, we do have gravitation. Gravity isn’t a force that acts instantly across the far reaches of space, but rather only propagates at the same speed all massless quanta move at: the speed of light. (Yes, the speed of gravity equals the speed of light.) All the rules that were formulated in special relativity still apply to the Universe, but to bring gravity into the fold, something extra was required: the notion that spacetime itself had an intrinsic curvature to it that depended on the presence of matter and energy within it.
It’s simple, in a sense: when you put a set of actors on a stage, that stage needs to bear the weight of the actors themselves. If the actors are massive enough and the stage isn’t perfectly rigid, the stage itself will deform owing to the presence of the actors.
The same phenomenon is at play with spacetime: the presence of matter and energy curves it, and that curvature affects both distances (space) and the rate at which clocks run (time). Moreover, it affects the two of them in an intricate way, where if you calculate the effects that matter and energy have on spacetime, the “spatial” effect and the “temporal” effects are related. Instead of the three-dimensional grid lines we envisioned in special relativity, those grid lines are now curved in General Relativity.

You can, if you like, conceptualize spacetime as a purely calculational tool and never go any deeper than that. Mathematically, every spacetime can be described by a metric tensor: a formalism that allows you to calculate how any field, line, arc, distance, etc., can exist in a well-defined way. The space can be flat or curved in an arbitrary way; the space can be finite or infinite; the space can be open or closed; the space can contain any number of dimensions. In General Relativity, the metric tensor is four dimensional (with three space dimensions and one time dimension), and the thing that determines the curvature of spacetime is the matter, energy, and stresses present within it.
In plain English, the contents of your Universe determine how spacetime is curved. You can then take the spacetime curvature and use it to predict how every quanta of matter and energy will move through and evolve in your Universe. The rules of General Relativity enable us to predict how matter, light, antimatter, neutrinos, and even gravitational waves will move through the Universe, and those predictions line up exquisitely with what we observe and measure.
What we don’t measure, though, is spacetime itself. We can measure distances and we can measure time intervals, but those are only indirect probes of the underlying spacetime. We can measure anything that interacts with us — our bodies, our instruments, our detectors, etc. — but an interaction only occurs when two quanta occupy the same point in spacetime: when they meet at an “event.”
We can measure every one of the effects that curved spacetime has on the matter and energy in the Universe, including:
- the redshifting of radiation due to the Universe’s expansion,
- the bending of light due to the presence of foreground masses,
- the effects of frame-dragging on a rotating body,
- the additional precession of orbits due to gravitational effects that go beyond what Newton predicted,
- how light gains energy when it falls deeper into a gravitational field and loses energy when it climbs out of it,
and many, many others. But the fact that we can only measure the effects of spacetime on the matter and energy in the Universe, and not the spacetime itself, tells us that spacetime behaves indistinguishably from a purely calculational tool.

But that doesn’t mean that spacetime itself isn’t a physically real entity. If you have actors acting out a play, you’d justifiably call the location where the play took place “their stage,” even if it was simply a field, a platform, bare ground, etc. Even if the play took place in the weightlessness of space, you’d simply note that they were using their freely-falling reference frame as a stage.
In the physical Universe, at least as we understand it, you cannot have quanta or interactions between them without the spacetime for them to exist in. Wherever spacetime exists, so do the laws of physics, and so do the fundamental quantum fields that underpin all of nature. In a sense, “nothingness” is the vacuum of empty spacetime, and talking about what occurs in the absence of spacetime is as nonsensical — at least from a physics perspective — as talking about a “where” that’s outside of the boundaries of space or a “when” that’s outside of the boundaries of time. Such a thing may exist, but we have no physical conception of it.

Perhaps most interestingly, when it comes to the nature of spacetime, there are so many questions that remain unanswered. Are space and time inherently quantum and discrete, where they themselves are divided up into indivisible “chunks,” or are they continuous? Is gravity inherently quantum in nature like the other known forces, or is it somehow non-quantum: a classical and continuous fabric all the way down to the Planck scale? And if spacetime is anything other than what General Relativity dictates it ought to be, how is it different, and in what way(s) will we be able to detect that?
But despite all the things that spacetime enables us to predict and know, it isn’t real in the same way that an atom is real. There’s nothing you can do to “detect” spacetime directly; you can only detect the individual quanta of matter and energy that exist within your spacetime. We’ve found a description of spacetime in the form of Einstein’s General Relativity that can successfully predict and explain every physical phenomenon we’ve ever observed or measured, but as far as exactly what it is — and whether it’s “real” or not — that’s not a question that science has yet discovered the answer to.





