Did the Universe have zero entropy when it first began?

One of the most inviolable laws in the Universe is the second law of thermodynamics. It tells us that, in any physical system, where nothing (no particles and no energy) is exchanged with the outside environment, entropy always increases. This is true not only of a closed and isolated system within our Universe, but of the entire Universe itself. If you look at the Universe today and compare it to the Universe at any earlier point in time, you’ll find that the entropy has always risen and continues to rise, with no exceptions, throughout all of our cosmic history.

But what if we go all the way back to the earliest times of all: to the very first moments of the Big Bang? What about even earlier: to the epoch of cosmic inflation that preceded and set up the hot Big Bang? If entropy has always increased, does that mean that the entropy of the Universe started from a value of zero at some initial time, and a state of what we might think of as “maximal organization” at some point?

The answer, perhaps surprisingly, is no. The Universe not only wasn’t maximally organized at the start of the Big Bang, but had quite a large entropy even at the earliest stages we can describe, during the hot Big Bang and even before. Moreover, “organized” isn’t quite a sound way to think about it, even though we use “disorder” as an offhand way to describe entropy. Let’s unpack what all of this means.

Our Universe, from the hot Big Bang until the present day, underwent a huge amount of growth and evolution, and continues to do so. Our entire observable Universe was approximately the size of a modest boulder some 13.8 billion years ago, but has expanded to be ~46 billion light-years in radius today. The complex structure that has arisen must have grown from seed imperfections of at least ~0.003% of the average density early on, and has gone through phases where atomic nuclei, neutral atoms, and stars first formed.

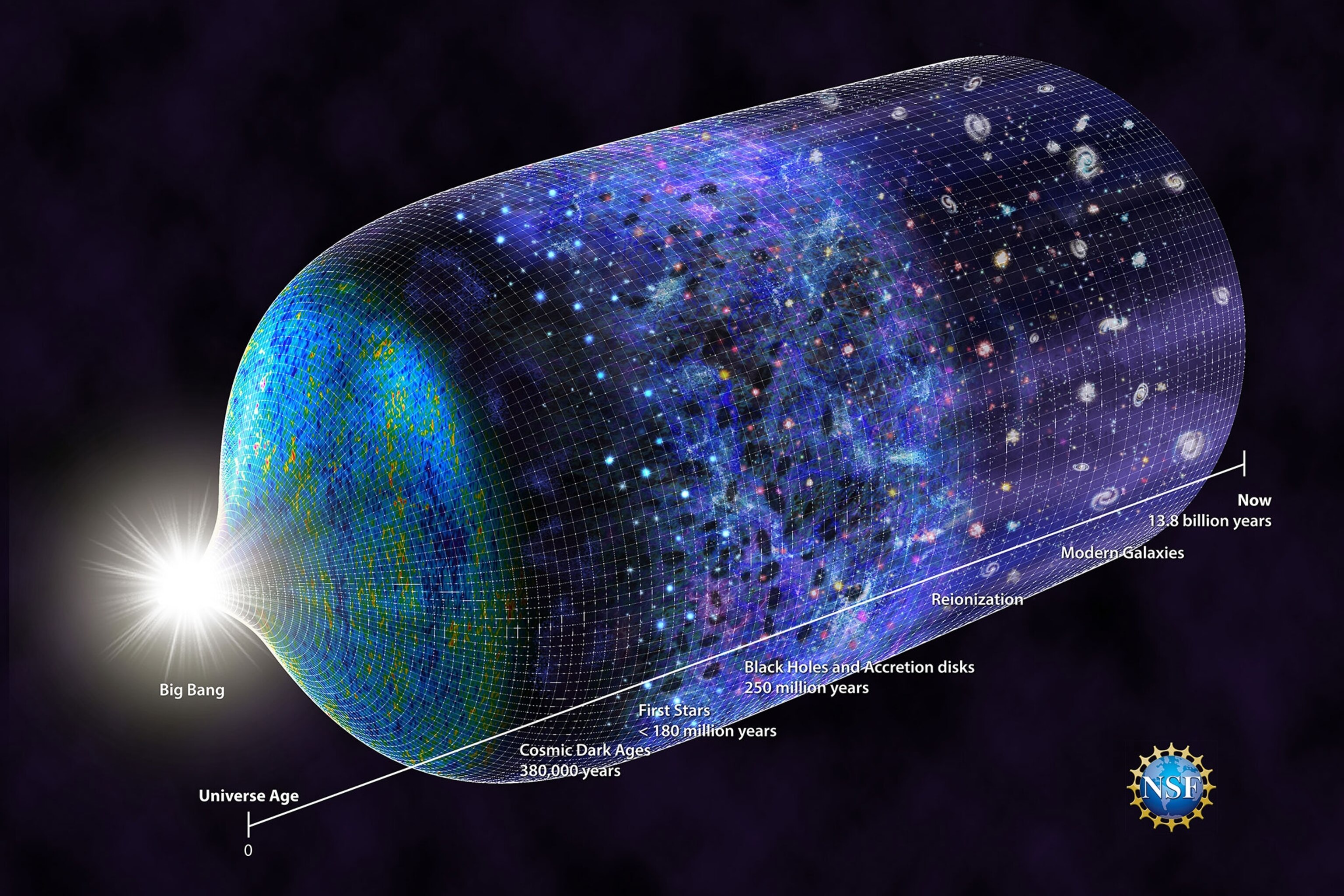
When we think about the Universe in the earliest stages of the hot Big Bang, we’re imagining all the matter and radiation that we have today — currently spread out across a sphere some ~92 billion light-years in diameter — packed into a volume about the size of the world’s largest pumpkin. The Universe back at that stage was incredibly hot and dense, with some 10⁹⁰ particles, antiparticles, and quanta of radiation all possessing enormous energies: energies that were billions of times greater than what even the Large Hadron Collider at CERN can achieve. This includes:

• all the matter particles of the Standard Model,
• all their antimatter counterparts,
• gluons,
• neutrinos,
• photons,
• whatever’s responsible for dark matter,
• plus any exotic species of particles that may have existed,

all packed into that tiny volume while possessing enormous kinetic energies. This hot, dense, expanding, and uniform to within 1 part in ~30,000 state would grow into the observable Universe we inhabit today over the next 13.8 billion years. Thinking about what we began with, however, it sure does seem like a thoroughly disordered state.

The early Universe was full of matter and radiation, and was so hot and dense that it prevented all composite particles, like protons and neutrons from stably forming for the first fraction-of-a-second. There was only a quark-gluon plasma, as well as other particles (such as charged leptons, neutrinos, and other bosons) zipping around at nearly the speed of light. This primordial soup consisted of particles, antiparticles, and radiation: a highly symmetric state.

But what does the appearance of disorder actually mean when it comes to entropy? We commonly talk about entropy as though it’s a measure of disorder:

• a broken egg on the floor has more entropy than an unbroken egg on the countertop,
• a cold dollop of cream next to a hot cup of coffee has less entropy than the well-mixed combination of the two,
• and a chaotic pile of clothes has a higher entropy than a neat set of dresser drawers with all the clothes folded and put away in an organized fashion.

While these examples all correctly identify the higher-entropy versus the lower-entropy state, it isn’t precisely “order” or “disorder” that allows us to quantify entropy.

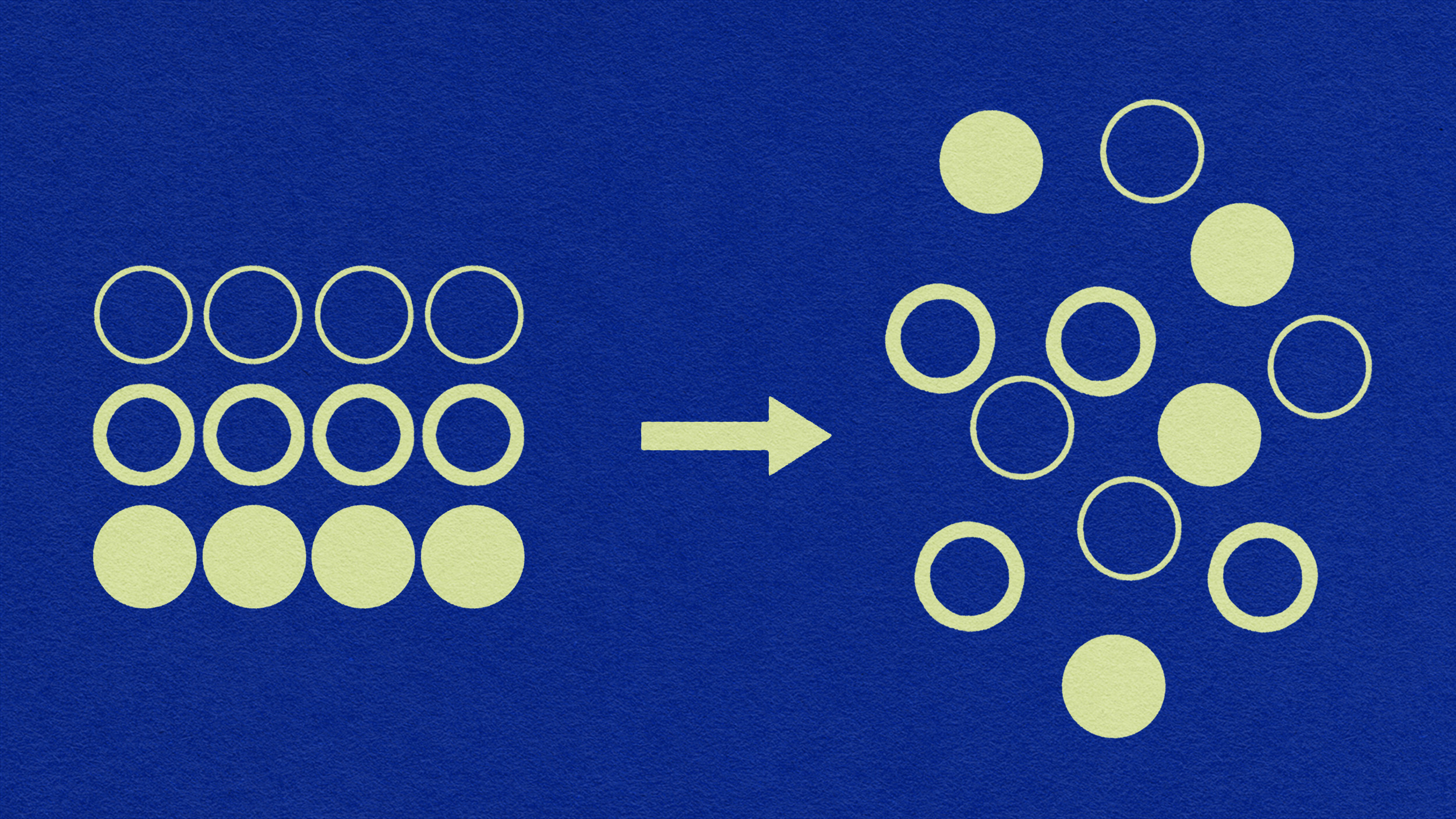
Instead, what we should be thinking about — for all the particles, antiparticles, etc., that are present in the system — is what the quantum state of each particle is, as well as what quantum states are allowed, given the energies and energy distributions at play. What entropy actually measures, rather than some nebulous characteristic like what humans call disorder, is simply this: the number of possible arrangements of the quantum state of your entire system.

A system set up in the initial conditions on the left and allowed to evolve will have less entropy if the door remains closed (left) than if the door is opened (right). If the particles are allowed to mix, there are more ways to arrange twice as many particles at the same equilibrium temperature than there are to arrange half of those particles, each, at two different temperatures, resulting in a much greater entropy for the system at right than the one at left.

Consider the two systems above, for example. On the left, a box with a divider in the middle has cold gas on one side and hot gas on the other; on the right, the divider has been opened so that the entire box is now filled with gas of the same (equilibrium) temperature. Which system has more entropy? The answer is the well-mixed one on the right, because there are more ways to arrange (or swap) the quantum states when all the particles have the same properties than when half have one set of properties and half have another, distinct set of properties.

Back in the era when the Universe was extremely young, it had a certain number of particles in it, with those particles possessing a specific energy distribution. Almost all of the entropy, in these early stages, was due to radiation; if we calculate it, then we find that the total entropy was around S = 10⁸⁸ k_B, where k_B is Boltzmann’s constant. However, every time an energy-emitting reaction occurred, such as:

• forming a neutral atom,
• fusing a light atomic nucleus into a heavier one,
• gravitationally collapsing a cloud of gas into a planet or star,
• or creating a black hole,

the overall entropy of the system — the entire Universe, in this case — would have to increase.

This snippet from a structure-formation simulation, with the expansion of the Universe scaled out, represents billions of years of gravitational growth in a dark matter-rich Universe. Over time, overdense clumps of matter grow richer and more massive, growing into galaxies, groups, and clusters of galaxies, while the less dense regions than average preferentially give up their matter to the denser surrounding areas.

Today, we are capable of quantifying the entropy of the Universe to within a certain degree of accuracy, and we find that the largest contributor to our Universe’s entropy is black holes. Given the number and mass of black holes present in today’s Universe, the entropy has reached a modern-day value that’s about a quadrillion times as large as it was in the earliest stages of the Big Bang: S = 10¹⁰³ k_B. For a black hole, the entropy is proportional to the black hole’s surface area, which is larger for heavier-mass black holes. The Milky Way’s relatively modest supermassive black hole, all on its own, has an entropy of approximately S = 10⁹¹ k_B, or around a factor of 1000 more than the entire Universe in the early stages of the hot Big Bang.

Over time, as the cosmic clock continues to tick by, the Universe continues to form and grow greater numbers of and higher mass black holes, while the heaviest black holes draw the greatest amounts of mass into them. About 10²⁰ years from now, entropy will reach its maximum, as perhaps up to 1% of the mass of the Universe (up from 0.04% today) will wind up being locked up in the form of black holes, giving us an entropy somewhere in the range of S = 10¹¹⁹ k_B to S = 10¹²¹ k_B, an entropy that will (likely) only be conserved, not created or destroyed, as these black holes eventually decay via Hawking radiation, which is an entropy-conserving (adiabatic) process.

Encoded on the surface of the black hole can be bits of information, proportional to the event horizon’s surface area. When the black hole decays, it decays to a state of thermal radiation. As matter and radiation fall into the black hole, the surface area grows, enabling that information to be successfully encoded. When the black hole decays, entropy will not decrease, but rather will remain constant, as Hawking radiation is an entropy-conserving (adiabatic) process.

However, this assumes that the entropy of our Universe applies only to the observable Universe, which expands tremendously over time. If we were to compare the entropy density of the Universe instead — in other words, the entropy of the observable Universe divided by its volume — we find that quantity, entropy density, winds up telling us a very different story.

A giant pumpkin, representing the size of the observable Universe shortly after the start of the hot Big Bang, with a radius of around 1.3 meters, has a volume of around 10 cubic meters, which means the very early Universe had an entropy density of a little over 10⁸⁷ k_B/m³, which is enormous. For a perhaps illuminating comparison, the Milky Way’s central black hole, on its own, occupies a volume of around 10⁴⁰ cubic meters, giving it an entropy density of only about 10⁵¹ k_B/m³, which is still extremely large, but a factor of some ~10³⁶ smaller than the entropy density was back during the earliest stages of the hot Big Bang.

In fact, if we look at the Universe today, even though the overall entropy is enormous, the fact that the volume is so large drives the entropy density to a relatively small number: somewhere in the range of ~10²⁷ k_B/m³ to 10²⁸ k_B/m³.

This simulation shows the cosmic web of dark matter and the large-scale structure it forms. Normal matter is present, but is only 1/6th of the total matter. Meanwhile, matter itself only composes about 2/3rds of the entire Universe, with dark energy making up the rest. Although the entropy of our entire Universe is enormous, dominated by supermassive black holes, the entropy density is remarkably small. Even though entropy always increases, in the expanding Universe, entropy density does not.

While it’s illuminating to note that the entropy density has dropped dramatically over time, it’s also important (perhaps even more important) to note that, despite the Universe’s relentless expansion, the actual calculable entropy of the Universe has increased tremendously. In fact, there’s a difference of about 15-to-16 orders of magnitude when we compare the entropy present in the early Universe, at the earliest moments of the hot Big Bang, compared with the entropy today. Over the cosmic history of the Universe, even though the expansion has diluted the entropy density — or the amount of entropy-per-unit-volume — the total entropy has increased by more than a factor of a quadrillion.

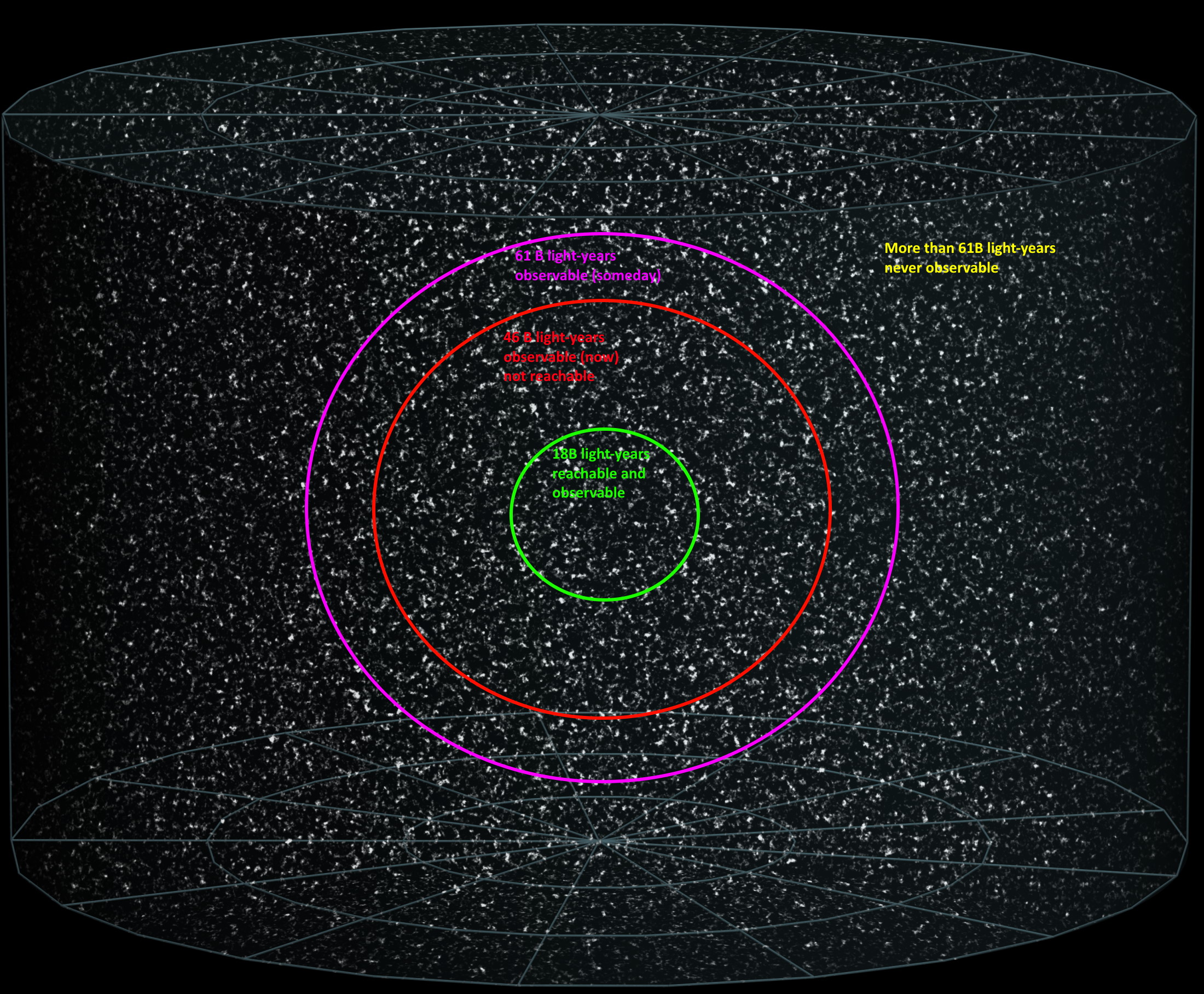
This difference will only be exacerbated, furthermore, if we decide to distinguish between the observable Universe, which we can see and measure today, and the unobservable Universe, which remains largely unknown to us. Although we can presently see for 46 billion light-years in all directions, and as time goes on, even more of the expanding Universe will eventually be revealed to us. We do not know its true size or extent; we can only place a lower limit on the size of the Universe beyond the part we can observe. For all we know, space might truly be infinite beyond the components of it that we can see.

In a Universe that comes to be dominated by dark energy, there are four regions: one where everything within it is reachable and observable, one where everything is observable but unreachable, one where things will someday be observable but aren’t today, and one where things will never be observable. The labeled numbers correspond to our consensus cosmology as of 2024, with boundaries of 18 billion light-years, 46 billion light-years, and 61 billion light-years separating the four regions.

Nevertheless, it’s important to remember that the Big Bang, although it’s the origin of our Universe as we know it, isn’t the very first thing of all that we can sensibly talk about. As far as we can tell, the Big Bang wasn’t the very beginning of our Universe at all, but rather describes a set of conditions — hot, dense, almost perfectly uniform, expanding, filled with matter, antimatter, and radiation, etc. — that existed at a very early time. In order to set up the Big Bang, however, the best evidence we have points to another state preceding the Big Bang: cosmic inflation.

According to inflation, before the Big Bang, the Universe was filled with a dark energy-like form of energy: energy inherent to either a field permeating the fabric of space or the very fabric of space itself. It was this form of energy, rather than particles, antiparticles or radiation, that dominated the Universe. As the Universe expanded, it did so exponentially: relentlessly, rather than at an ever-decreasing rate determined by the falling density of matter and radiation. During this time, for however long inflation endured, with every ~10^-32 s or so that passed, a region the size of the Planck length, the smallest scale at which the laws of physics don’t break down, gets stretched to the size of today’s presently visible Universe.

Exponential expansion, which takes place during inflation, is so powerful because it is relentless. With every ~10^-35 seconds (or so) that passes, the volume of any particular region of space doubles in each direction, causing any particles or radiation to dilute and causing any curvature to quickly become indistinguishable from flat. After only a few hundred doubling times, or ~10^-32 seconds, a fluctuation that was initially smaller than the Planck scale would now be stretched to be larger than the presently observable Universe.

During inflation, the entropy of our Universe must have been much, much lower: around 10¹⁵ k_B for a volume equivalent to the size of our observable Universe at the start of the hot Big Bang: a value that you can get by calculating the Unruh radiation that gets generated by the presence of a cosmological horizon. But the most important aspect of the story is this: the actual entropy of whatever was present in the Universe before inflation doesn’t particularly change all that much during the process of inflation; it simply gets diluted. The initial entropy density changes dramatically, getting diluted very rapidly until it becomes negligible, as whatever pre-existing entropy was present in the Universe prior to inflation still remains, but gets progressively stretched across larger and larger volumes.

This is vital to understanding what happens in our Universe during the early stages. We don’t need some miraculously low-entropy state to occur to begin our Universe or to begin the process of inflation. All we need is for inflation to arise in some volume of the Universe, even a small one, and for the space within that volume to begin inflating. In short order — after no more than a tiny fraction of a second — no matter how much entropy there initially was, that initial entropy now becomes spread out over a much larger volume. Entropy may always be increasing, but the entropy density, or the amount of entropy contained in the volume that will someday become our entire observable Universe, drops to this extremely low value driven by Unruh radiation: about 10 nanojoules-per-Kelvin, spread out over the volume of whatever the size of the Universe was at that moment.

During an inflationary period (highlighted in green), world lines get stretched by the exponential expansion (horizontal axis), causing a tremendous drop in entropy density (the amount of entropy present within the blue circles), even though the overall entropy of the Universe can never decrease. When inflation ends, the field energy locked up in inflation gets converted into particles, resulting in an enormous entropy increase: the largest increase in cosmic history, in fact.

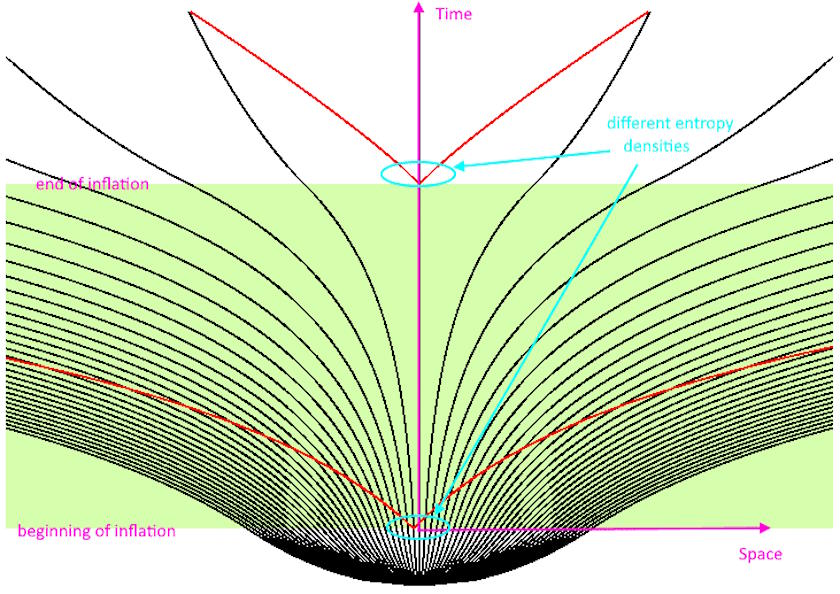
When inflation ends, that energy that was driving the exponential expansion then gets converted into matter, antimatter and radiation: that hot, dense, almost uniform, and expanding-but-cooling state that signifies the onset of the hot Big Bang. Converting that field energy into particles causes the entropy within our observable Universe to rise dramatically at that moment: by about 73 orders of magnitude from the final stages of inflation to the beginning of the hot Big Bang. Over the next 13.8 billion years, as our Universe expanded, cooled, fused, gravitated, formed atoms and stars and galaxies and black holes and planets and humans, our entropy “only” rose by an additional 15 or 16 orders of magnitude, where it continues to rise today.

What has occurred and what will occur over the entire history of the Universe is peanuts compared to the biggest entropy growth spurt to ever happen: the end of inflation and the beginning of the hot Big Bang. Yet even during that inflationary state, with alarmingly low entropy, we still never saw the entropy of the Universe decrease; it was only the entropy density that went down as the volume of the Universe increased exponentially. In the far future, when the Universe expands to about 10 billion times its present radius, the entropy density will once again be as small as it was during that inflationary epoch from long ago. While the entropy within our cosmic volume will keep on increasing, the entropy density will keep dropping, and will never be as large as it was at the start of the hot Big Bang: some 13.8 billion years ago.