Why does the proton spin? Physics holds a surprising answer

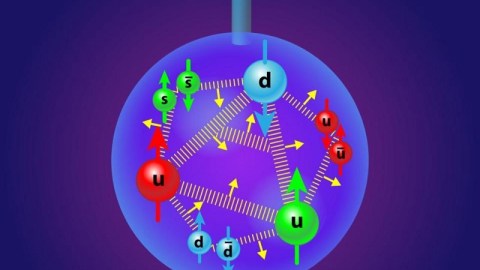
It’s tempting to add the spins of the quarks together, but that’s not what the experiments agree with!

“We must regard it rather as an accident that the Earth (and presumably the whole solar system) contains a preponderance of negative electrons and positive protons. It is quite possible that for some of the stars it is the other way about.” –Paul Dirac

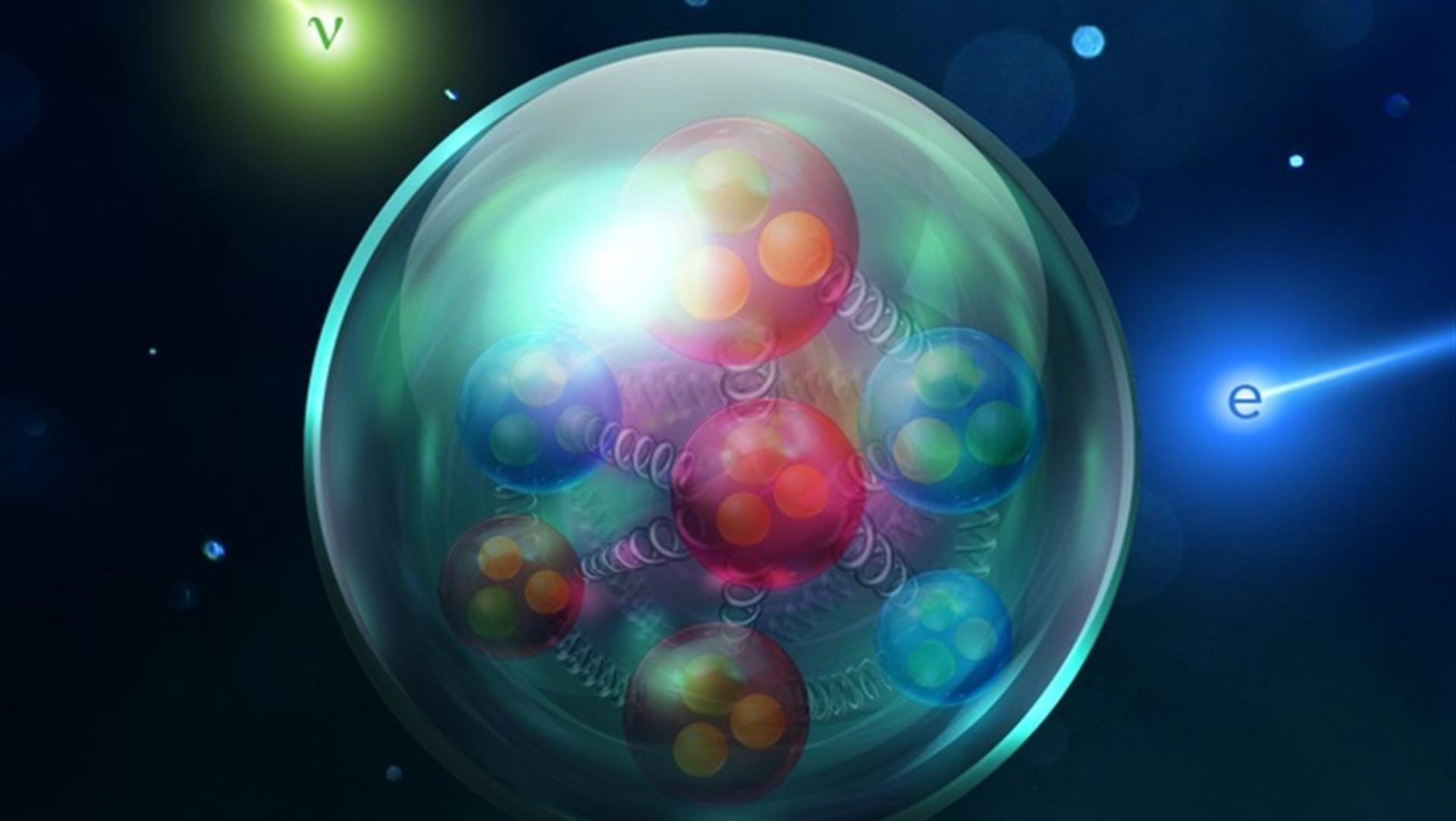
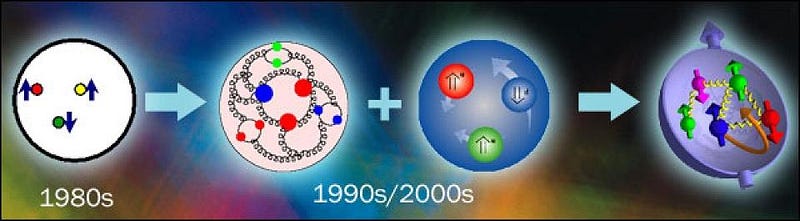
You can take any particle in the Universe and isolate it from everything else, yet there are some properties that can never be taken away. These are intrinsic, physical properties of the particle itself — properties like mass, charge, or angular momentum — and will always be the same for any single particle. Some particles are fundamental, like electrons, and their mass, charge and angular momentum are fundamental, too. But other particles are composite particles, like the proton. While the proton’s charge (of +1) is due to the sum of the three quarks that make it up (two up quarks of +2/3 and one down quark of -1/3), the story of its angular momentum is much more complicated. Even though it’s a spin = 1/2 particle, just like the electron, simply adding the spins of the three quarks that make it up together isn’t enough.

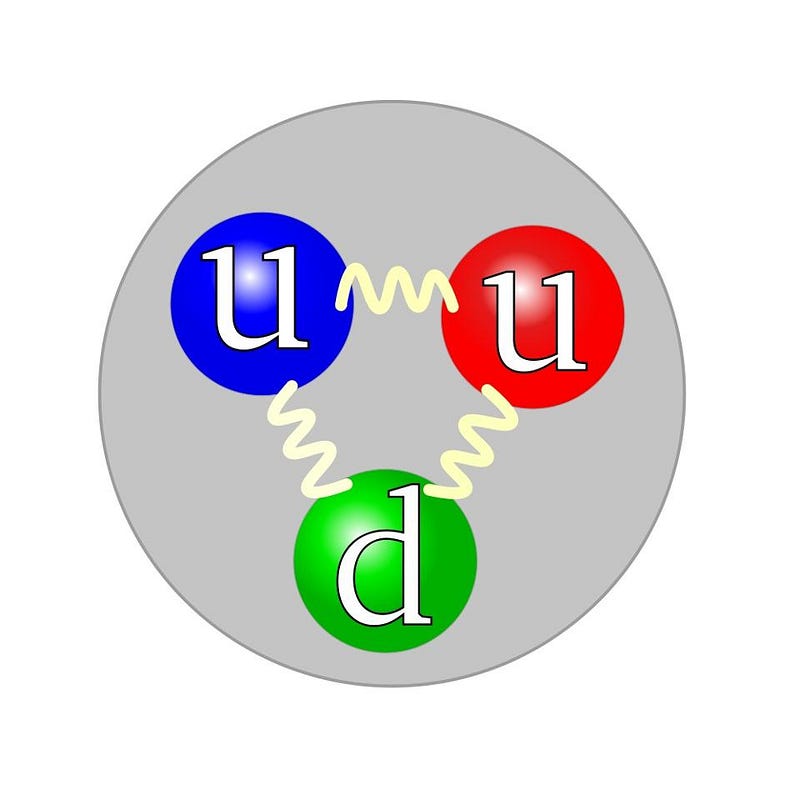
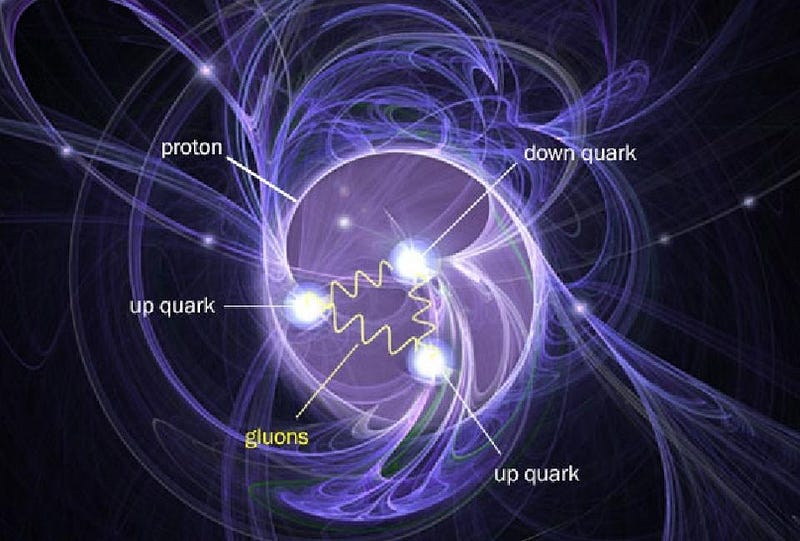
There are two things that contribute to angular momentum: spin, which is the intrinsic angular momentum inherent to any fundamental particle, and orbital angular momentum, which is what you get from two or more fundamental particles that make up a composite particle. (Don’t be fooled: no particles are actually, physically spinning, but “spin” is the name we give to this property of intrinsic angular momentum.) A proton has two up quarks and one down quark, and they’re held together by gluons: massless, color-charged particles which mutually bind the three quarks together. Each quark has a spin of 1/2, so you might simply think that so long as one spins in the opposite direction of the other two, you’d get the proton’s spin. Up until the 1980s, that’s exactly how the standard reasoning went.

With two up quarks — two identical particles — in the ground state, you’d expect that the Pauli exclusion principle would prevent these two identical particles from occupying the same state, and so one would have to be +1/2 while the other was -1/2. Therefore, you’d reason, that third quark (the down quark) would give you a total spin of 1/2. But then the experiments came, and there was quite a surprise at play: when you smashed high-energy particles into the proton, the three quarks inside (up, up, and down) only contributed about 30% to the proton’s spin.

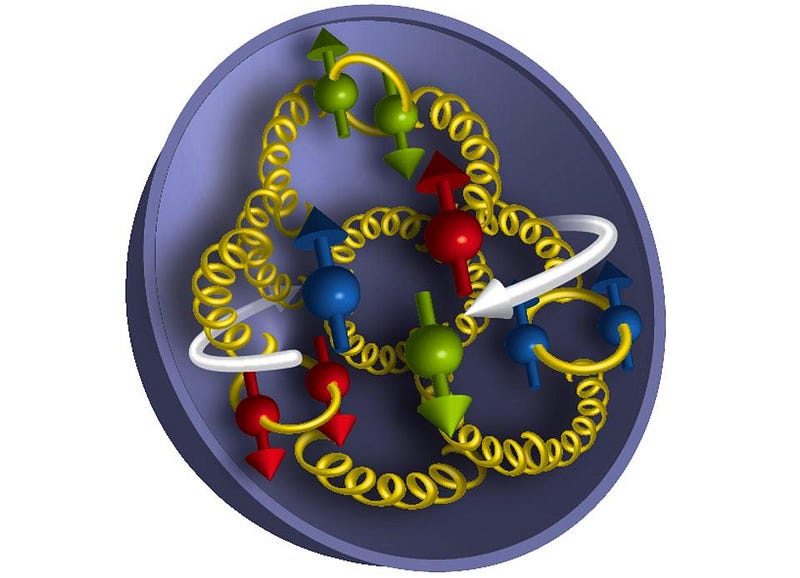
There are three good reasons that these three components might not add up so simply.

1. The quarks aren’t free, but are bound together inside a small structure: the proton. Confining an object can shift its spin, and all three quarks are very much confined.
2. There are gluons inside, and gluons spin, too. The gluon spin can effectively “screen” the quark spin over the span of the proton, reducing its effects.
3. And finally, there are quantum effects that delocalize the quarks, preventing them from being in exactly one place like particles and requiring a more wave-like analysis. These effects can also reduce or alter the proton’s overall spin.

In other words, that missing 70% is real.

Maybe, you’d think, that those were just the three valence quarks, and that quantum mechanics, from the gluon field, could spontaneously create quark/antiquark pairs. That part is true, and makes important contributions to the proton’s mass. But as far as the proton’s angular momentum goes, these “sea quarks” are negligible.

Maybe, then, the gluons would be an important contributor? After all, the standard model of elementary particles is full of fermions (quarks and leptons) which are all spin = 1/2, and bosons like the photon, the W-and-Z, and the gluons, all of which are spin = 1. (Also, there’s the Higgs, of spin = 0, and if quantum gravity is real, the graviton, of spin = 2.) Given all the gluons inside the proton, perhaps they matter, too?

There are two ways to test that: experimentally and theoretically. From an experimental point of view, you can collide particles deep inside the proton, and measure how the gluons react. The gluons that contribute the most to the proton’s overall momentum are seen to contribute substantially to the proton’s angular momentum: about 40%, with an uncertainty of ±10%. With better experimental setups (which would require a new electron/ion collider), we could probe down to lower-momentum gluons, achieving even greater accuracies.

But the theoretical calculations matter, too! A calculational technique known as Lattice QCD has been steadily improving over the past few decades, as the power of supercomputers has increased exponentially. Lattice QCD has now reached the point where it can predict that the gluon contribution to the proton’s spin is 50%, again with a few percent uncertainty. What’s most remarkable is that the calculations show that — with this contribution — the gluon screening of the quark spin is ineffective; the quarks must be screened from a different effect.

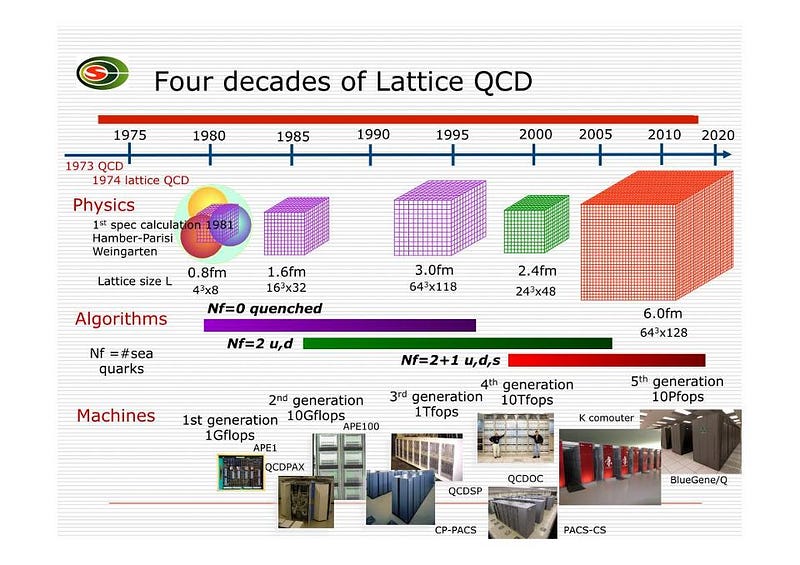
The remaining 20% must come from orbital angular momentum, where gluons and even virtual pions surround the three quarks, since the “sea quarks” have a negligible contribution, both experimentally and theoretically.

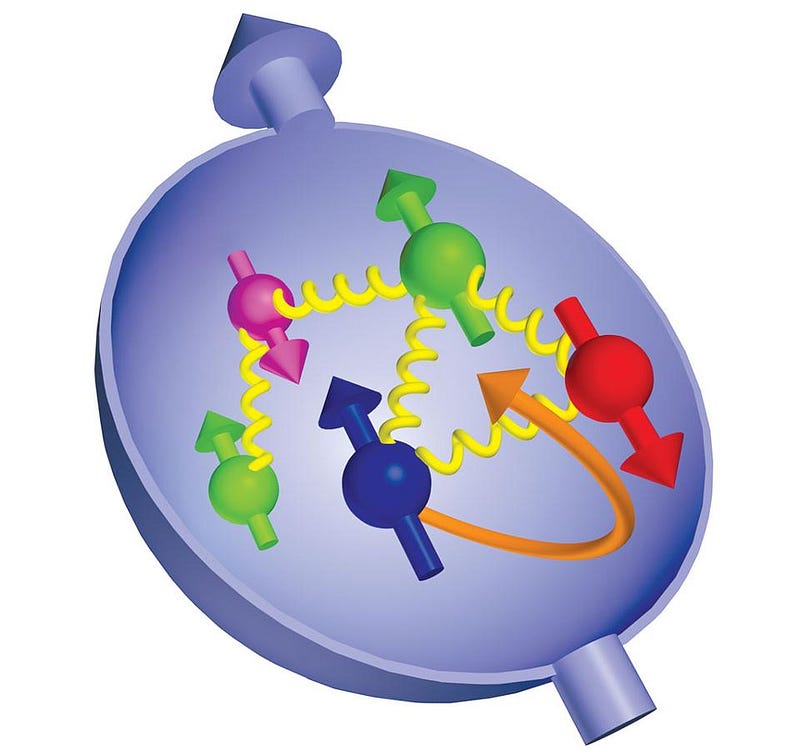
It’s remarkable and fascinating that both theory and experiment agree, but most incredible of all is the fact that the simplest explanation for the proton’s spin — simply adding up the three quarks — gives you the right answer for the wrong reason! With 70% of the proton’s spin coming from gluons and orbital interactions, and with experiments and Lattice QCD calculations improving hand-in-hand, we’re finally closing in on exactly why the proton “spins” with the exact value that it has.

Starts With A Bang is based at Forbes, republished on Medium thanks to our Patreon supporters. Order Ethan’s first book, Beyond The Galaxy, and pre-order his next, Treknology: The Science of Star Trek from Tricorders to Warp Drive!