Ask Ethan #43: Decaying Gravitational Orbits
If you thought “planets move about the sun in ellipses,” wait until you read this.
“I much prefer the sharpest criticism of a single intelligent man to the thoughtless approval of the masses.” –Johannes Kepler, 1601
When it comes to the questions and suggestions that I get for Ask Ethan, some of them really dive deeply into the limit of science and scientific knowledge. As a theorist, our goal is to create models that are complex enough that they accurately predict all the relevant phenomena in a system, yet simple enough that we can solve them. Well, this week’s question comes from Alex B., editor of RealClearScience, who asks the following:
Does orbital decay (e.g., merger of binary stars) indicate that there is something wrong with Newton’s and Kepler’s laws? Does relativity help explain it?
Let’s back up to the very beginning, and come all the way to Newton’s and Kepler’s laws.
By treating the Sun as a fixed, stationary point in space, we could track the astronomical motion of all the heavenly bodies — planets, asteroids and comets — around the Sun. Using the best data available to the world at the time (over 400 years ago), Kepler figured out that each one of the planets didn’t move in a circle centered on the Sun at all, but rather in an elliptical path with the Sun at one focus. More than half a century later, Newton figured out the gravitational law that would cause these orbits to happen: Newton’s universal law of gravitation.
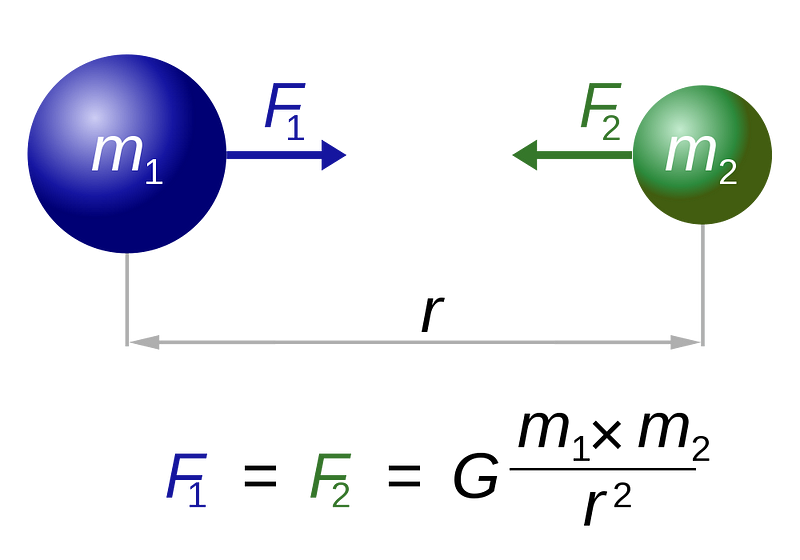
Now, this law didn’t just apply to the planets orbiting the Sun or the objects in space, nor to merely falling objects here on Earth. No, this law was called “universal” because it applied equally to any object with mass in the entire Universe.
In other words, if you knew, at any instant in time, the locations and masses of everything present in the Universe, you would be able to deterministically predict how everything would evolve under the influence of gravity infinitely far into the future. That’s the full power of Newton’s law.

But we don’t need to simulate the entire Universe, in fact, that’s a terrible idea! For one thing, it would take a computer as powerful as the entire Universe to run that simulation to the same accuracy that the Universe itself runs it. What we prefer to do, rather than compute this force individually for all the subatomic, point particles in the Universe and the way they interact with one another, is we make a simple model.
So what if we take a very simple system: our Solar System with just the planets and the Sun, and apply Newton’s laws to that?
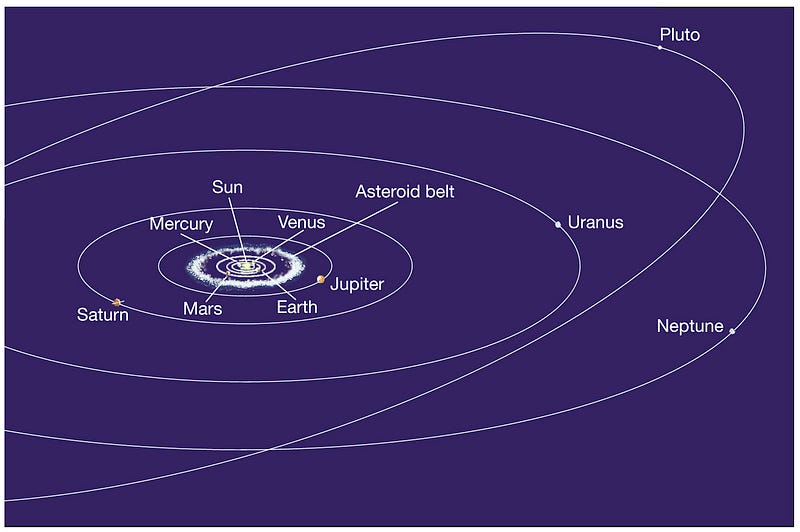
You might think that, with these nine masses separated by huge distances, we’d get eight ellipses moving around a stationary Sun.
Well, that’s what you’d get if you made the following set of assumptions:
- All the planets and the Sun can be treated as point-like masses.
- Each planet’s orbit is determined only by the force that the Sun exerts on it. And finally,
- That Newton’s laws are so absolute that there’s no such things as Lorentz invariance (or that the laws of physics don’t care how quickly you’re moving, in this particular case).
In reality, of course, none of these things are true.

The planets and the Sun are not point-like at all. While the distances separating them from one another are very large compared to their physical sizes, their actual sizes range from giant (Mercury is 4,879 km in diameter) to gargantuan (the Sun’s is 1,391,684 km). Their masses are all unevenly distributed, being more dense in their core and less dense as we move radially outward, and every body in the Solar System rotates with some non-zero intrinsic angular momentum.
Keep this last part about the rotation in mind as we move forward; we’ll need it again in just a bit.
The other planets make a big difference, especially over long periods of time, on one another’s orbits! In reality, none of the planets make perfect ellipses, and the Sun isn’t stationary at all. The gravitational forces that the planets exert on one another and also on the Sun ensure that these orbits aren’t constant in time at all, but rather that — if we’re precise enough in our calculations and measurements — we should be able to see that Kepler’s orbital predictions are just an approximation.
In reality, planetary orbits never make a closed ellipse, and small amounts of orbital energy are lost over time as even more complex phenomena, like collisions with other particles, are taken into account.
But it’s the last one that’s a killer, and it was first noticed before relativity was ever developed: by Oliver Heaviside back in 1893.
Let’s say you have a central mass that creates a gravitational field around it. In addition, that mass is moving in some capacity (remember, the Sun is not stationary), so that gravitational field is going to change over time. And finally, you have another massive particle moving through that gravitational field. Well, what’s going to happen?
It’s okay to not know. You see, around the same time, scientists were considering the problem of what happens when an electrically charged particle moves through an electric field. In particular, they imagined the atom as a positively charged nucleus orbited by a negatively charged electron. Do you know what happens there?
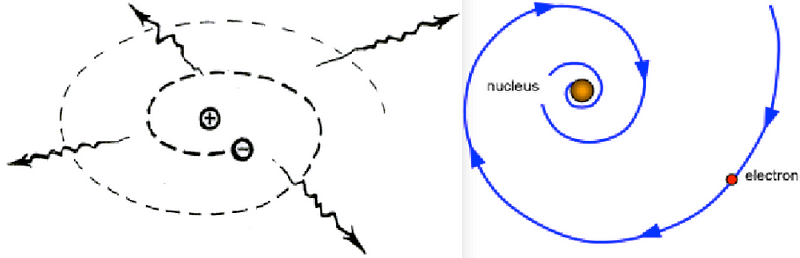
The fast-moving particle will emit electromagnetic radiation, which carries energy. The orbit, therefore, will decay over time, and therefore matter should be unstable! Rutherford discovered this problem for electromagnetism, and it wasn’t resolved until quantum mechanics came around decades later.
But for gravitation, this is where we run up against the limits of what Newton’s laws can predict. Because Newtonian gravity doesn’t care what your velocity is, it predicts that there should be no gravitational radiation as you accelerate (i.e., change your direction) in orbit in a gravitational field. That’s the flaw of a theory not being Lorentz invariant. (Electromagnetism, to the contrary, is Lorentz invariant.)
But just like there’s electromagnetism, there should be gravitomagnetism as well, so long as gravitation really is Lorentz invariant. You may have heard a lot of hoopla surrounding Gravity Probe B, but in truth, there’s already a more precise measurement of gravitomagnetism that’s been readily available for some time.
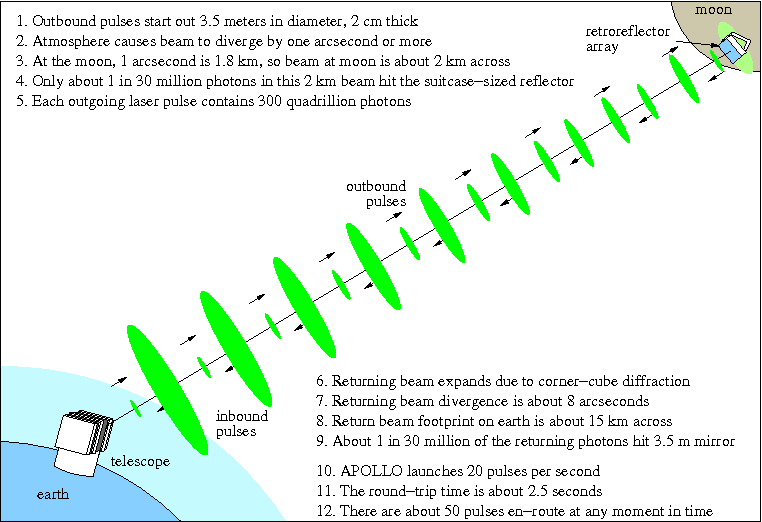
By measuring the Moon’s position precisely using laser ranging — something we’ve been doing for around 45 years now — we’ve been able to not only confirm the gravitomagnetism effect (the same effect responsible for orbital decays), but to discover that it agrees with General Relativity’s predictions to 99.9% confidence, with 0.1% uncertainty.
For a system like Earth, it will take 10^150 years for our planet to spiral into the Sun, much longer than the lifetime of our Solar System. But for a system like the binary pulsar, it’s doomed in just a few hundred million years, due to this gravitational radiation effect alone!
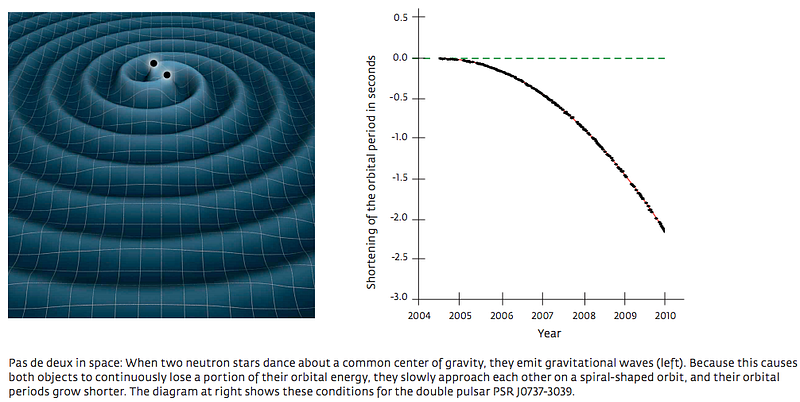
So there is a component of Newton’s laws that explains the departure from closed, perfect ellipses when it comes to orbits, but if you want to fully account for the orbital decays we observe, you need a theory that is Lorentz invariant — that keeps the laws of physics the same regardless of what your velocity is — and General Relativity, even after all these years, is still the one that works the absolute best!
So thanks for a great question, Alex, and I hope you learned something new about gravitomagnetism. If you have a question or suggestion you’d like to see featured on Ask Ethan, send it in, and the next one could be yours!
Leave your comments at the Starts With A Bang forum on Scienceblogs.





