Ask Ethan #78: Why does E=mc^2?
Einstein’s most famous equation works out more neatly than you’d expect.
“It followed from the special theory of relativity that mass and energy are both but different manifestations of the same thing — a somewhat unfamiliar conception for the average mind.” –Albert Einstein
Some concepts in science are so world-altering — so profound — that almost everyone knows what they are, even if they don’t fully understand them. So why not work on that together? Each week, you send in your questions and suggestions, and I choose my favorite to share the answer to with the world. This week’s honor goes to Mark Leeuw, who asks:
Einstein came up with E=mc^2. But the units of energy, mass, time and length were already established before Einstein. So, how comes it equals up so nicely? Why isn’t there a constant in the equation to make up for our assumptions (of length, time, ….) ? Why isn’t it E=amc^2 with ‘a’ being an arbitrary constant?
Things could have been a little different, if only our Universe weren’t wired this way. Let’s see what we’re talking about.

On the one hand, we have objects with mass: from galaxies, stars and planets all the way down to molecules, atoms and fundamental particles themselves. As tiny as they might be, every single constituent of what we know as matter has the fundamental property of mass, which means that even if you take all of its motion away, even if you slow it down so that it’s completely at rest, it still has an influence on every other object in the Universe.

Specifically, it still exerts a gravitational pull on everything else in the Universe, no matter how far away that object is. It tries and attract everything else to it, it experiences an attraction to everything else, and also, it has a specific amount of energy inherent to its very existence.
This last part is a little counterintuitive, since we normally think of energy, at least in physics, as the ability to accomplish some task: what we call the ability to do work. What can you accomplish if you’re just sitting there, boring, at rest?
Before we answer that, let’s look at the other side of the coin: things without a mass.
On the other hand, then, there are totally massless things in the Universe: light, for instance. These particles, too, carry certain amounts of energy, something that’s easy to understand from the fact that they can interact with things, be absorbed by them, and transfer that energy to them. Light of sufficient energies can heat up matter, impart additional kinetic energy (and velocity) to them, kick electrons up to higher energies in atoms, or ionize them completely, all depending on their energy.
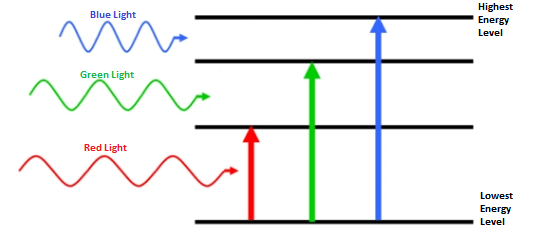
Moreover, the amount of energy a massless particle (like light) contains is determined solely by its frequency and wavelength, whose product always equals the speed that the massless particle moves at: the speed of light. Larger wavelengths, therefore, mean smaller frequencies and hence lower energies, while shorter wavelengths mean higher frequencies and higher energies. While you can slow a massive particle down, attempts to remove energy from a massless particle will only lengthen its wavelength, not slow it in the least.

So with all of this in mind, how does mass-energy equivalence work? Yes, I can take a particle of antimatter and a particle of matter (like an electron and a positron), collide them together, and get massless particles (like two photons) out. But why are the energies of the two photons equal to the mass of the electron (and positron) times the speed of light squared? Why isn’t there another factor in there; why does the equation have to be exactly equal to E = mc^2?

Interestingly enough, if the special theory of relativity is true, the equation must be E = mc^2 exactly, with no departures allowed. Let’s talk about why this is. To start, I want you to imagine you have a box in space, that’s perfectly stationary, with two mirrors on either side, and a single photon traveling towards one mirror inside.
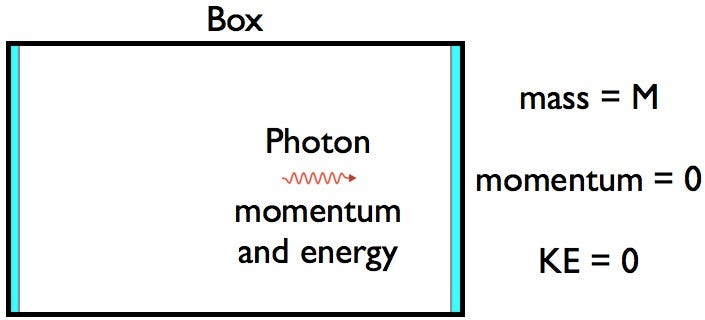
Initially, this box is going to be perfectly stationary, but since photons carry energy (and momentum), when that photon collides with the mirror on one side of the box and bounces off, that box is going to begin moving towards the direction that the photon was initially traveling in. When the photon reaches the other side, it’s going to reflect off of the mirror on the opposite side, changing the momentum of the box back to zero. It will continue to reflect like this, with the box moving towards one side half the time, and remaining stationary for the other half of the time.
In other words, this box is going to, on average, be moving, and hence — since the box has mass — it’s going to have a certain amount of kinetic energy to it, all thanks to the energy of that photon. But what’s also important to think about is momentum, or what we consider as the quantity of an object’s motion. Photons have a momentum that’s related to their energy and wavelength in a known and straightforward way: the shorter your wavelength and the higher your energy, the higher your momentum.
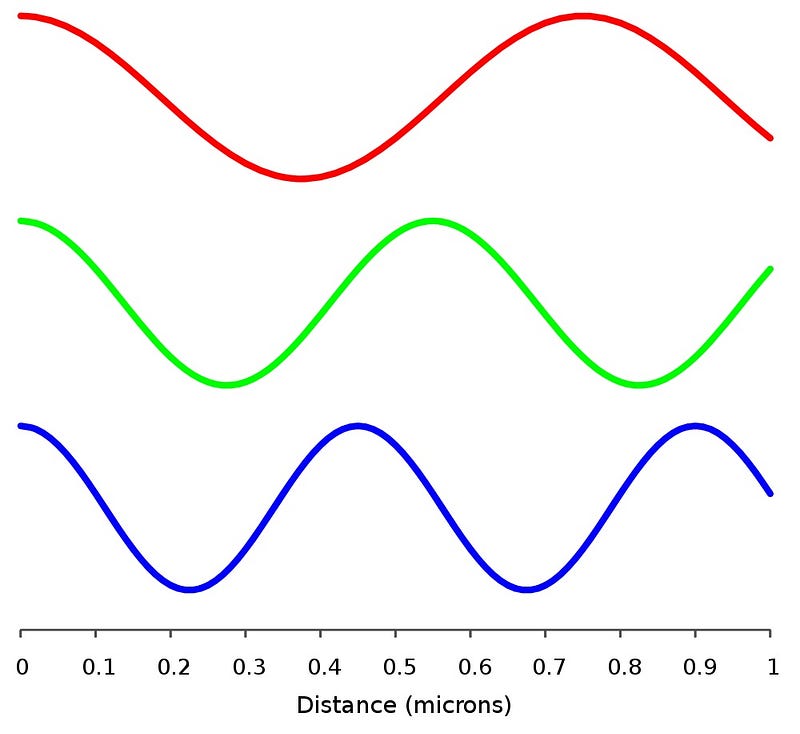
So let’s think about what this might mean: we’re going to do a thought experiment. I want you to think about what happens when it’s just the photon moving, all by itself, at the beginning. It’s going to have a certain amount of energy and a certain amount of momentum intrinsic to it. Both of these quantities have to be conserved, so right now the photon has the energy determined by its wavelength, the box only has the energy of its rest mass — whatever that is — and the photon has all the momentum of the system, while the box has a momentum of zero.
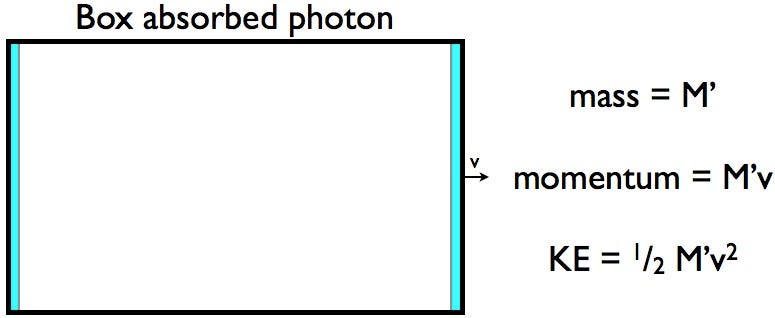
Now, the photon collides with the box, and is temporarily absorbed. Momentum and energy both need to be conserved; they’re both fundamental conservation laws in this Universe. If the photon’s absorbed, that means there’s only one way to conserve momentum: to have the box move with a certain velocity in the same direction the photon was moving.
So far, so good, right? Only now, we can look at the box, and ask ourselves what its energy is. As it turns out, if we go off of the standard kinetic energy formula — KE = ½mv^2 — we presumably know the mass of the box and, from our understanding of momentum, its speed. But when we compare the energy of the box with the energy that the photon had before the collision, we find that the box doesn’t have enough energy now!
Is this a crisis of some sort? No; there’s a simple way to resolve it. The energy of the box/photon system is the box’s rest mass plus the kinetic energy of the box plus the energy of the photon. When the box absorbs the photon, much of the photon’s energy has to go into increasing the mass of the box. Once the box absorbs the photon, its mass is different (and increased) from what it was before it interacted with the photon.
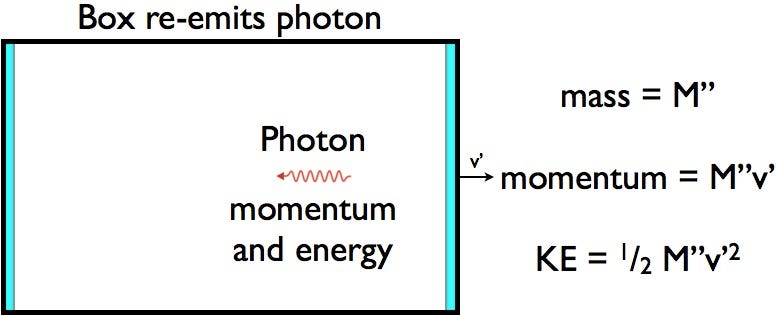
When the box re-emits that photon in the opposite direction, it gets even more momentum and speed in the forward direction (balanced by the photon’s negative momentum in the opposite direction), even more kinetic energy (and the photon has energy, too), but it has to lose some of its rest mass in order to compensate. When you work out the mathematics (shown three different ways here, here and here, with some good background here), you find that the only energy/mass conversion that allows you to get both energy conservation and momentum conservation together is E = mc^2.

Throw in any other constant in there and the equations don’t balance, and you gain-or-lose energy each time you absorb-or-emit a photon. Once we finally discovered antimatter in the 1930s, we saw firsthand the verification that you can turn energy into mass and back into energy with the results matching E = mc^2 exactly, but it was thought experiments like this one that allowed us to know the results decades before we ever observed it. Only by identifying a photon with an effective mass equivalent of m = E/c^2 can we conserve both energy and momentum. Although we say E = mc^2, Einstein first wrote it this other way, assigning an energy-equivalent-mass to massless particles.
So thanks for a great question, Mark, and I hope this thought experiment helps you understand why you not only need there to be an equivalence between mass and energy, but how there’s only one possible value for the “constant” in that equation that will conserve both energy and momentum together, something our Universe seems to require. The only equation that works? E = mc^2. If you’ve got a question or suggestion you’d like to see featured on Ask Ethan, send yours in! You never know, the next feature could be yours.
Leave your comments at the Starts With A Bang forum on Scienceblogs!





