Ask Ethan: Can Free Quarks Exist Outside Of A Bound-State Particle?

There are rules absolutely forbidding it from happening. But some particles do it anyway.

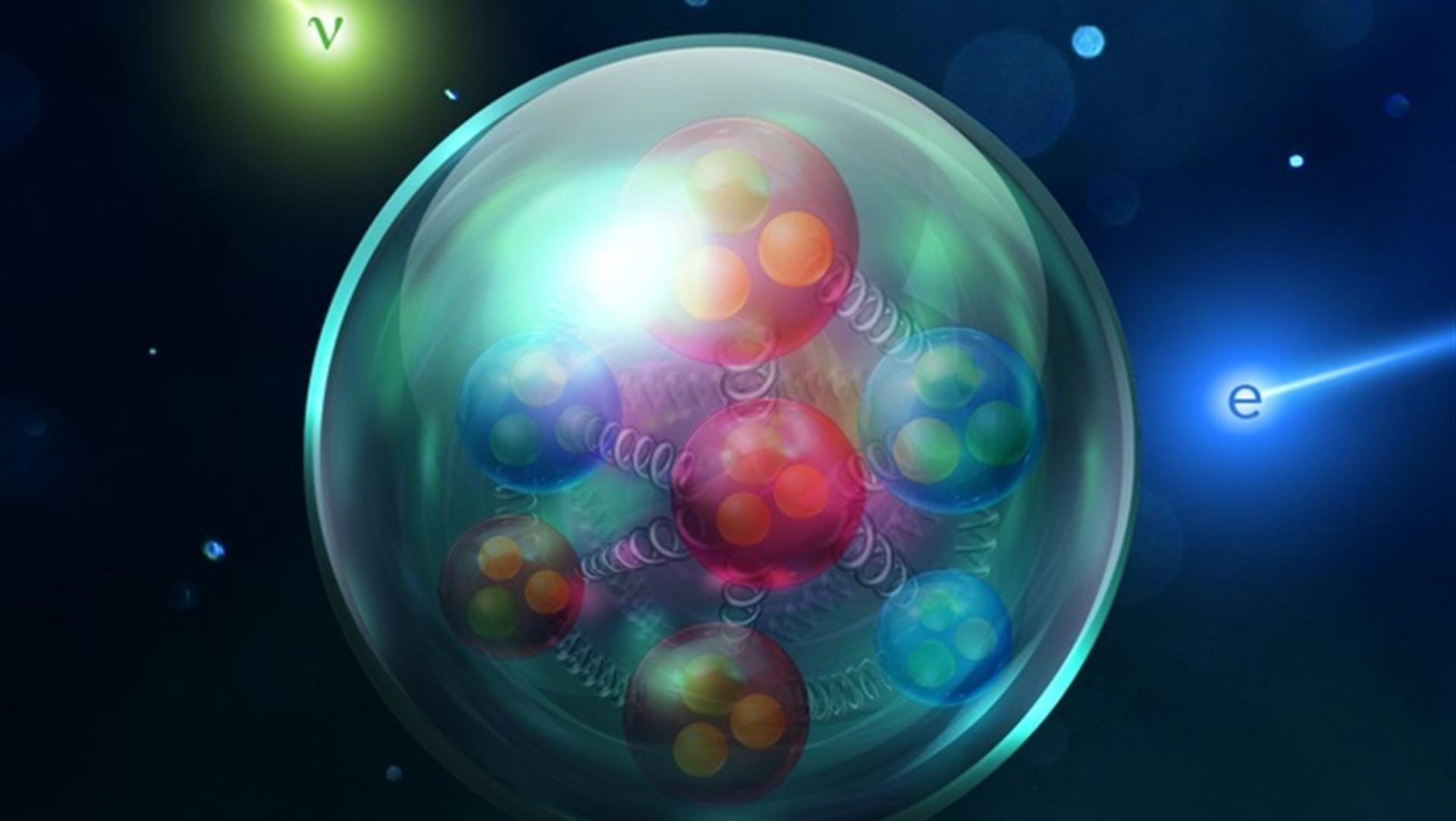
All the matter we know of in the Universe is made up of Standard Model particles. Photons and neutrinos zip through the Universe all the time, far outnumbering all the other particles. Normal, atom-based matter is far less in number, but far more important in terms of mass and energy. Each atom is composed of electrons, the lightest charged lepton, and an atomic nucleus composed of protons and neutrons. Inside each proton and neutrons, though, are quarks and gluons: the constituents of all baryons and mesons we’ve ever created from particle accelerators and cosmic rays. But what about quarks outside of those bound states? Could they possibly exist? That’s what Katie Bacher wants to know, inquiring:

Can quarks can exist outside an elementary particle?

Don’t worry, Katie, I know what you mean. Let’s take a deep dive and find out!

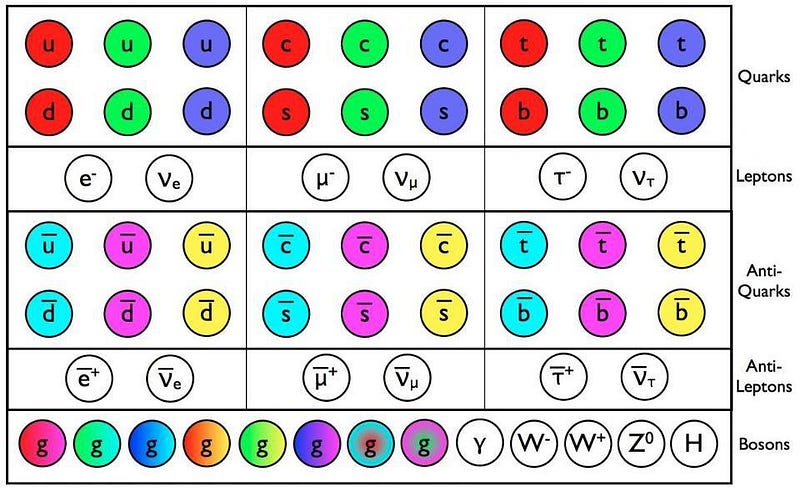
The Standard Model of elementary particles represents our fullest understanding of all the matter whose properties are known in our Universe. The fermions, which include the quarks and leptons, all have mass and fundamental charges that determine which forces act on them. The bosons are the particles responsible for the forces and interactions between the fermions.

Fermions with electric charges (all the quarks and the charged leptons) couple to the photon; they experience the electromagnetic force.

Fermions with weak isospins/hypercharges couple to the W/Z bosons; they experience the weak force and also weak (radioactive) decays.

And fermions with color charges, which are only the quarks (and antiquarks), interact with the strong force, mediated by the gluons.

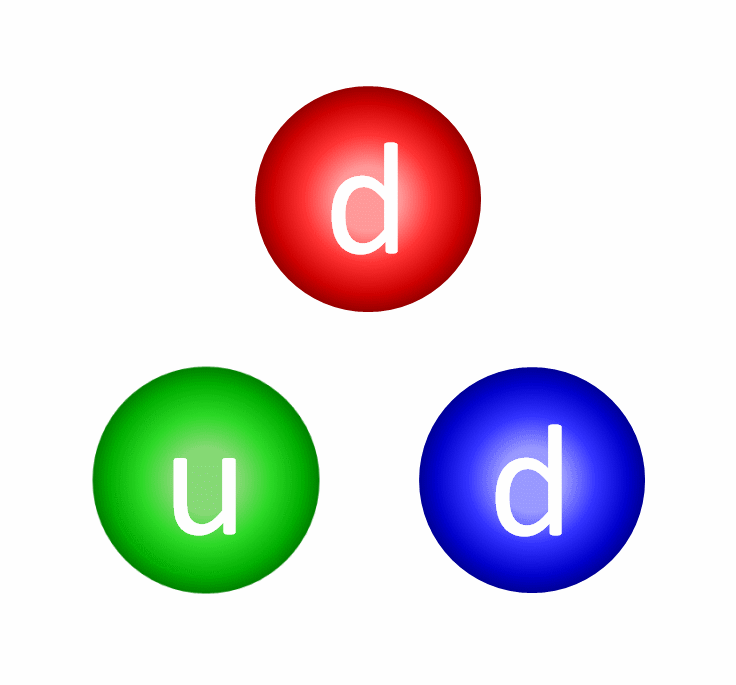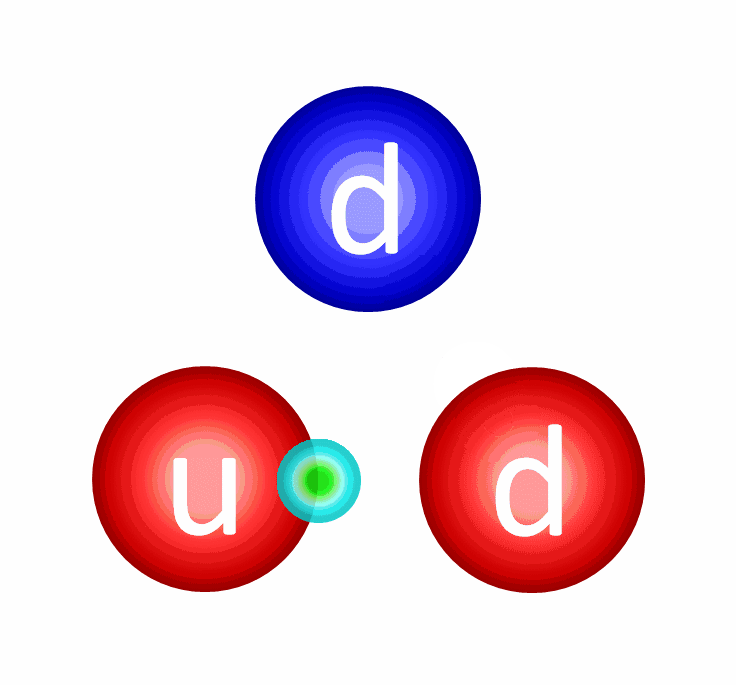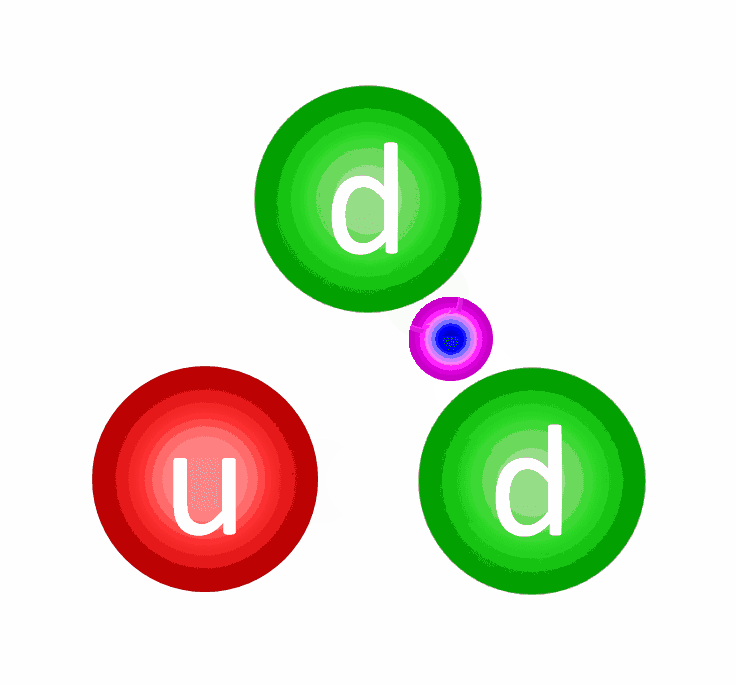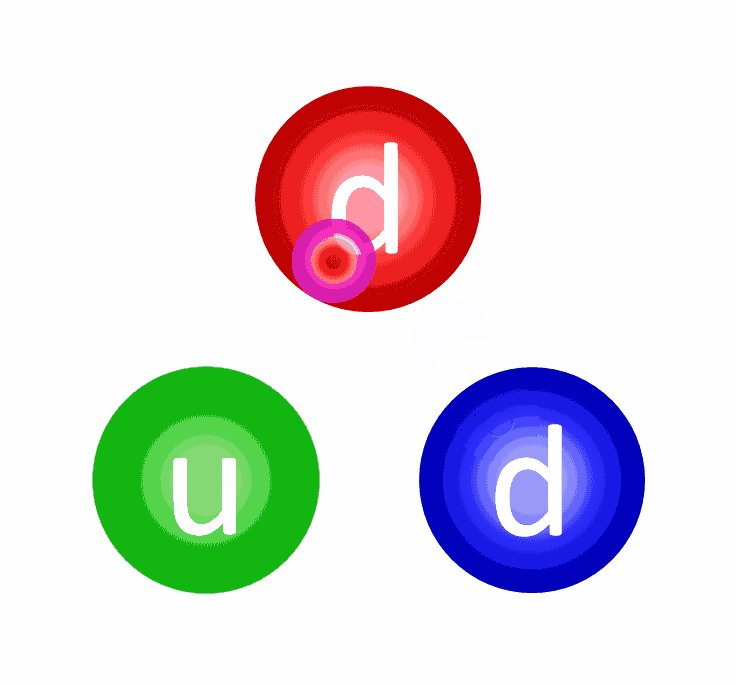
The quarks, you’ll remember, also have electric charges, and the electric force is pretty simple:

• the closer your charges are to each other, the greater in strength the force is,
• the greater in magnitude your charges are, the greater the force they experience,
• and charges of opposite signs attract while charges of the same sign repel.

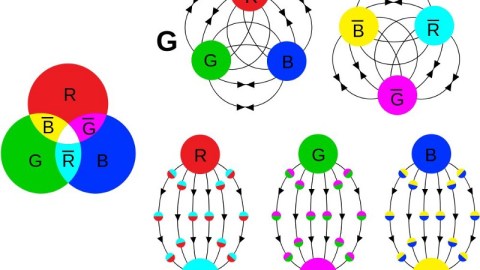
But the strong force, which acts on color, is fundamentally different in two important ways. First, instead of one type of charge (always positive and attractive, like gravity) or two types of charge (positive and negative, like electromagnetism), there are three types of color charge: red, green, and blue. And second, when color charges get close to one another, the force drops to zero; it’s only when you separate them that the force gets substantial.

This property of the strong interactions, known as asymptotic freedom, is a surprising, counterintuitive property not found in any of the other fundamental forces.

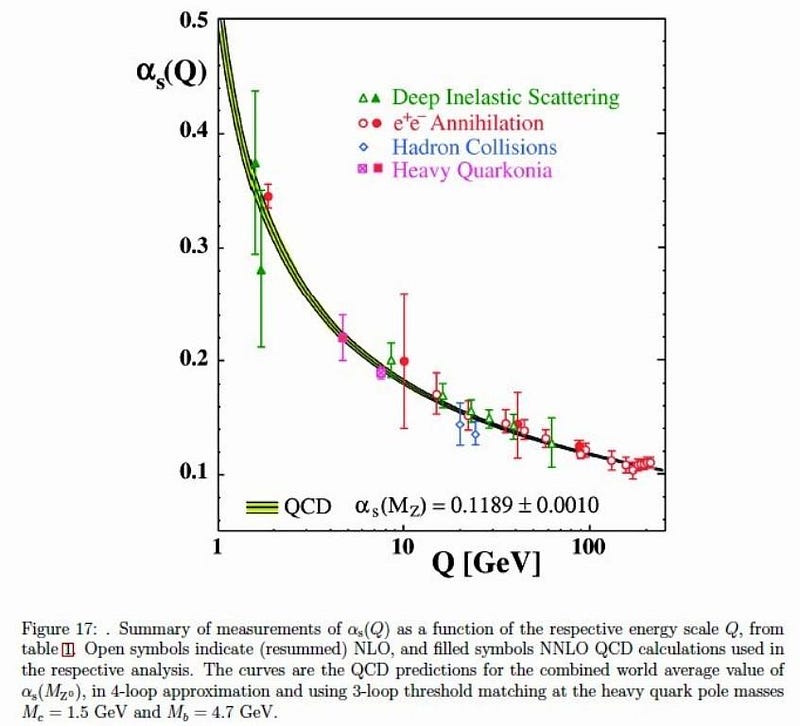
I’ve previously written a big tutorial on how the strong force works, so let’s just summarize two basic points that are relevant to the question at hand.

1. The strong force is of a greater magnitude than any other force in the Universe, except on extremely short distance scales, where it approaches zero as the distance goes to zero.
2. All stable configurations of quarks, antiquarks, and gluons have zero net color, which requires either three quarks (because red + blue + green sum to colorless), three antiquarks (because cyan + yellow + magneta sum to colorless), or a quark-antiquark (because cyan = anti-red, yellow = anti-blue, and magneta = anti-green) combination, or multiples thereof.

There is no known way, under the laws of physics, to have an interaction that produces a net color; if you produce a color, you must produce an equal amount of its anti-color.

If our goal is to produce an unbound, free quark that’s outside of any composite, bound-state particle, we’ll have to be clever. Unfortunately, most of the clever attempts you’ll think of at first will fail for reasons that aren’t very intuitive.

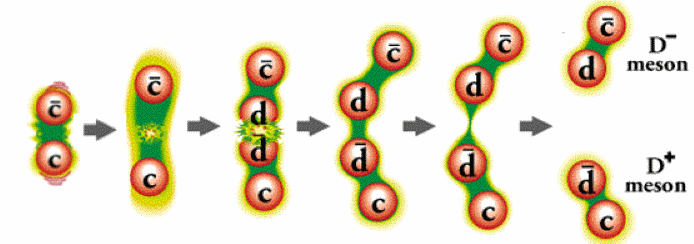
You might think to take a meson — a quark/antiquark combination — and to try to pull these two particles away from each other. If you can pull them apart hard enough, overcoming the strong force, maybe you’d rip these two particles free and have isolated color charges along with free quarks.

It’s a nice idea, but it falls apart in practice. It turns out that once you input a certain amount of energy in your attempt to rip these two particles apart, you’ve suddenly created an antiquark/quark pair (via Einstein’s E = mc2) spontaneously out of the vacuum. In your attempt to pull these particles apart, you’ve simply spontaneously created two mesons where you only had one previously.

You might think about taking two composite particles, like protons, and smashing them together at the fastest speeds you can: at almost the speed of light. After all, perhaps through this approach you’d be able to knock a quark (or antiquark, or gluon, or two or three) out of the bound state it was previously in, but with extraordinary speeds and energies. Perhaps, with your ultra-sophisticated detectors, you’d be able to even see it.

Unfortunately, when we do exactly this and set up our detectors, we don’t see free, unbound quarks passing through them. Instead, we see enormous numbers of composite, bound-state particles all moving in the same direction: what particle physicists call a jet event. Because of the rules of QCD, the theory governing the strong interactions, these free particles are prohibited, and so they undergo what’s called hadronization, where multiple baryons and/or mesons are formed out of the would-be free quark or gluon.

These scenarios might not give you the free quark that you’re seeking, but that doesn’t mean free quarks are impossible. Instead, thinking about how and why these attempts failed can lead us to understand how creating free quarks is, in fact, possible!

The first important thing to take note of is that all forces, even the strong force, take time to exert their influence on real particles. In order to have a bound state of quarks (or quarks and antiquarks), you have to have a gluon leave one particle and arrive at the other. Just as we wouldn’t notice for 8 minutes and 20 seconds if the Sun suddenly stopped emitting photons — or planet Earth wouldn’t notice for that same amount of time if the Sun suddenly disappeared and stopped gravitationally attracting the Earth — a particle can’t feel the strong force from another if it doesn’t live for long enough to do so.

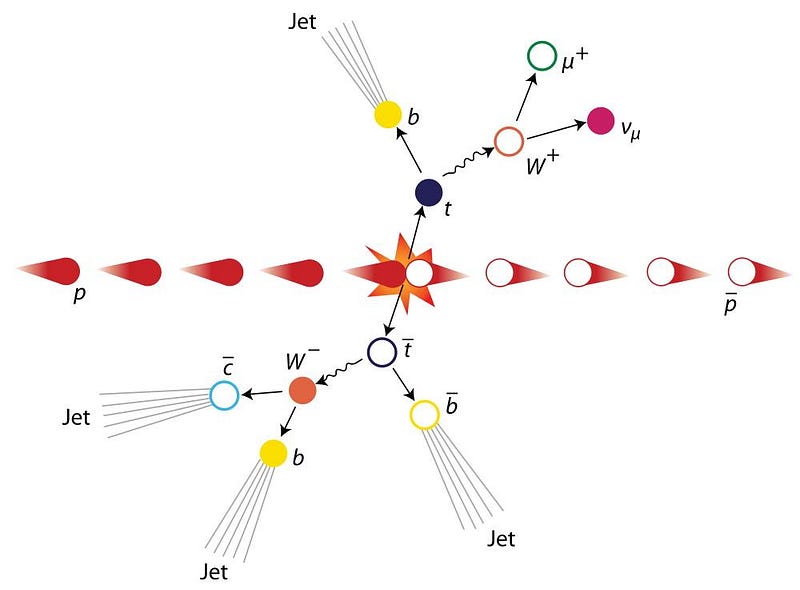
This happens in particle physics for the heaviest of all the Standard Model particles: the top quark. The first way to produce a free quark that isn’t bound to others as a part of a composite, colorless particle is to create a quark that doesn’t live long enough to get there. With a mean lifetime of 5 × 10^-25 seconds, the top quark (along with its antiquark counterpart) simply doesn’t exist for long enough to hadronize. It simply decays.

That’s one of the known ways to make a free quark, but it’s not particularly satisfying. You might wonder if there’s any way to take the matter that we know of — you know, like the matter in our own bodies — and have those quarks exist in a state where they’re not part of any bound, composite particle. And there is; all we have to do is remember the idea of asymptotic freedom, and then create a state where quarks are dense and hot enough that there are no discernible baryons and/or mesons.

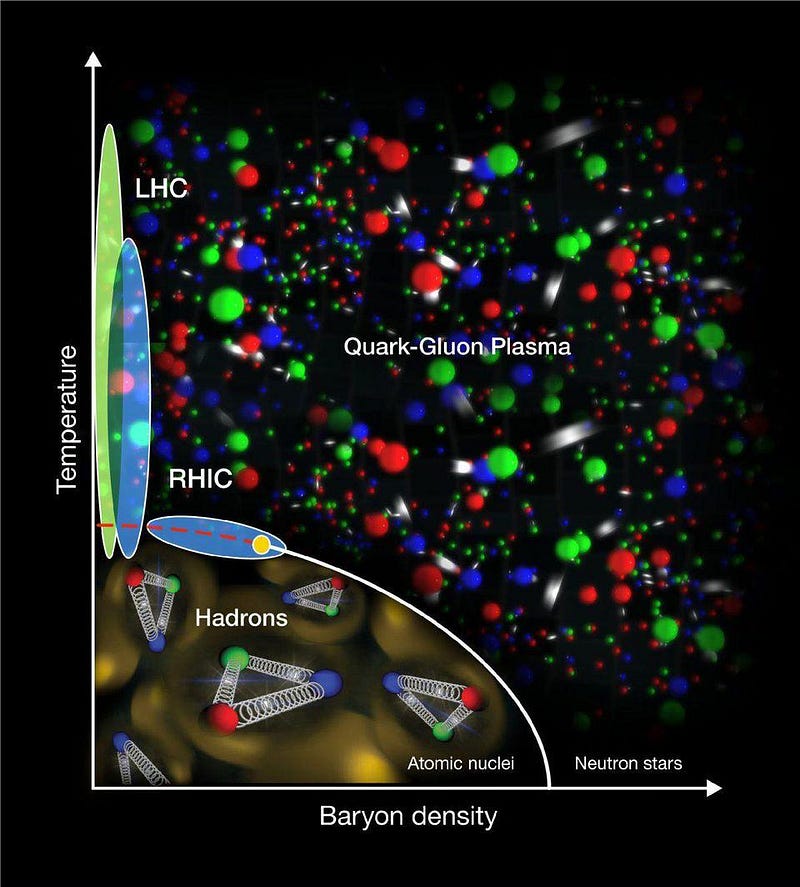
Instead of hadrons like baryons and mesons, this would create a state known as a quark-gluon plasma, where the temperature and/or density of particles is so great that you cannot tell where one bound state ends and another begins. It’s all just one massive mess of quarks and/or antiquarks in a soup where gluons are constantly exchanged between any quarks/antiquarks within one another’s reach.

Quark-gluon plasmas have been created in laboratory settings: at particle accelerators that collide not just individual protons, but large, massive, heavy atomic nuclei. This was accomplished at RHIC, the relativistic heavy ion collider in Brookhaven, and also (at higher energies) at the Large Hadron Collider. Quark-gluons plasmas get created at these colliders due to their high energies and temperatures, rather than their ultra-high densities.

A similar state existed in the early Universe, for the first microsecond (or so) after the hot Big Bang. But, much like in the case of the quark-gluon plasmas we create in colliders, the particles move apart from one another and cool rather rapidly, forming hadrons in short order. While the Universe was completely filled with free, unbound quarks and antiquarks at the very beginning, that state didn’t last for very long at all.

You might wonder, then, if there’s any possibility of having a long-lived state where free quarks exist. And there is, but you have to go to the ultimate extremes. Inside the core of a massive neutron star, before you reach the mass threshold that would necessitate its collapse into a black hole, the individual neutrons making up the star could reach such high densities that it fundamentally becomes a quark-gluon plasma. In some scenarios, it wouldn’t simply be made of the light (up and down) quarks, but strange quarks as well.

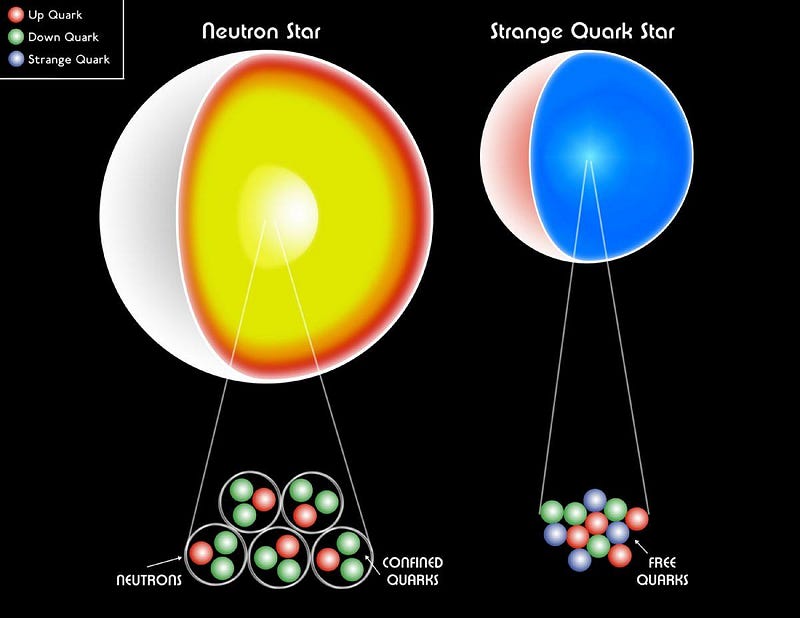
In our low-energy, modern-day Universe, we only find quarks and antiquarks in bound, hadronic states: baryons, anti-baryons and mesons. But that’s only because the quarks that conventionally exist are long-lived, at low densities, and at low enough energies and temperatures. If we change any one of those three, the existence of free quarks is not only possible, but mandatory.

If the conditions for forming a bound state aren’t met, then confinement is impossible. The four ways we know how to get there are to create a top quark, to look to the early stages of the hot Big Bang, to collide heavy ions together at relativistic speeds, or to look inside the densest objects (like neutron stars or the hypothetical strange quark stars) to find the quark-gluon plasma inside. It’s not an easy feat to accomplish, but if you want to create matter in the most extreme states we know of, you have to go to extreme ends to get there.

Send in your Ask Ethan questions to startswithabang at gmail dot com!