Ask Ethan: Do virtual particles really exist?

When we think about the Universe on a fundamental level, we normally think about how to break up everything contained within it into the smallest components of nature. Matter can be broken down into atoms, which break down into nuclei and electrons. Nuclei can be further broken down into protons and neutrons, with quarks and gluons inside of them. Other indivisible particles, like photons and neutrinos, also permeate the Universe, along with the other particles of the Standard Model and whatever — assuming it’s particle-like in nature — happens to be responsible for dark matter.
If you take all these quanta away, however, is there anything left? Is the empty space that houses these particles truly empty without them, or does the mere fact that we have quantum fields in our Universe mean that empty space is actually filled with something physical? That’s the question of Chuckles Davis, who writes in to ask:
“[you’ve written about] how virtual particles have real observable effects and how Quantum Fluctuations were experimentally proven a long time ago… and when [Neil de Grasse] Tyson explained nothing, he talks about how virtual particles appear and disappear, but other quantum mechanics shows like PBS space time has said they are calculatory tools, so which is it? There are so many conflicting statements that I don’t know which is right.”
It sounds like you’re ready for the true story behind the idea of virtual particles and quantum fields. Let’s explore what’s actually real.
When it comes to physics, the first thing you must understand is that it’s inherently an experimental science. This doesn’t mean that theoretical endeavors don’t have their uses; the interplay between theory and experiment is how science evolves and advances over time. But it does mean that if we want to make the claim that something exists, its existence:
- must affect some sort of measurable or observable quantity,
- in a quantifiable and predictable manner,
- that we can then go out and measure or observe,
- performing those test past a certain critical precision.
If we can clear those hurdles, we can either confirm that these predictions are validated and the expected effects are seen, or to invalidate those predictions and demonstrate that some other set of effects (or no effect) occurs instead. It is only through measurement and observation that a physical theory, idea, concept, or hypothesis can gain any sort of robust support from the evidence.
The idea behind quantum physics, when it began, was simple enough. Max Planck’s quantum hypothesis, designed to explain how hot objects emitted light (in the form of blackbody radiation), postulated that light could only be emitted or absorbed in discrete, individual energy packets: quanta. The energy of an individual quantum of light, today called a photon, would equal the frequency of that light multiplied by Planck’s constant. Energy was quantized, energy quanta behaved probabilistically, all forms of matter and quantized energy acted as both waves and particles, all with Planck’s constant as the fundamental constant of the quantum realm.
These observations of early quantum behavior were later solidified into modern quantum mechanics, where:
- every quantum could be described by a wavefunction,
- the wavefunction describes the relative probabilities of specific outcomes,
- the wavefunction spreads out and evolves in space and over time,
- certain uncertainty relations and exclusion rules are obeyed,
- and when an interaction occurs — where energy is exchanged between two quanta — the wavefunction occupies just one specific quantum state at that instant.
Every particle, fundamental and composite, obeyed these novel quantum rules, containing elements of both waves and particles within them.
But the initial formulations of quantum mechanics had some issues. For one, they weren’t relativistically invariant. This means that two different observers moving relative to one another, and hence experiencing time differently, would get two different, inconsistent predictions. Breakthroughs were made in relativistic quantum mechanics, leading to the Klein-Gordon, Dirac, and Proca equations. But even so, there was a problem when you did something even as simple as bring two electrons close together.
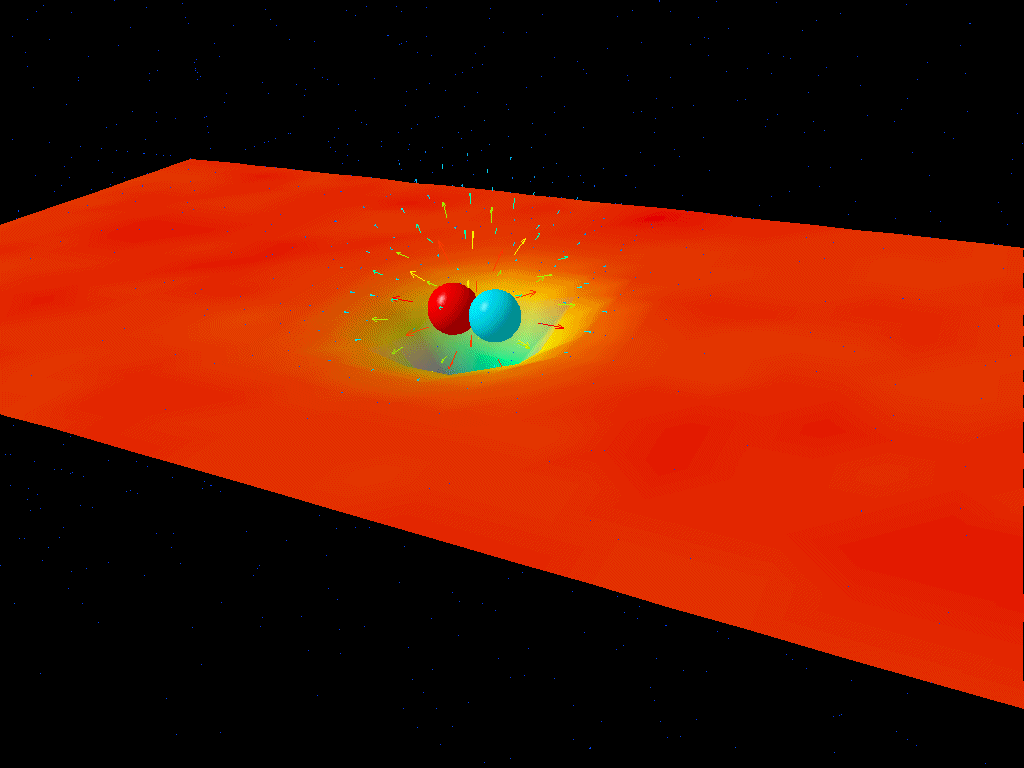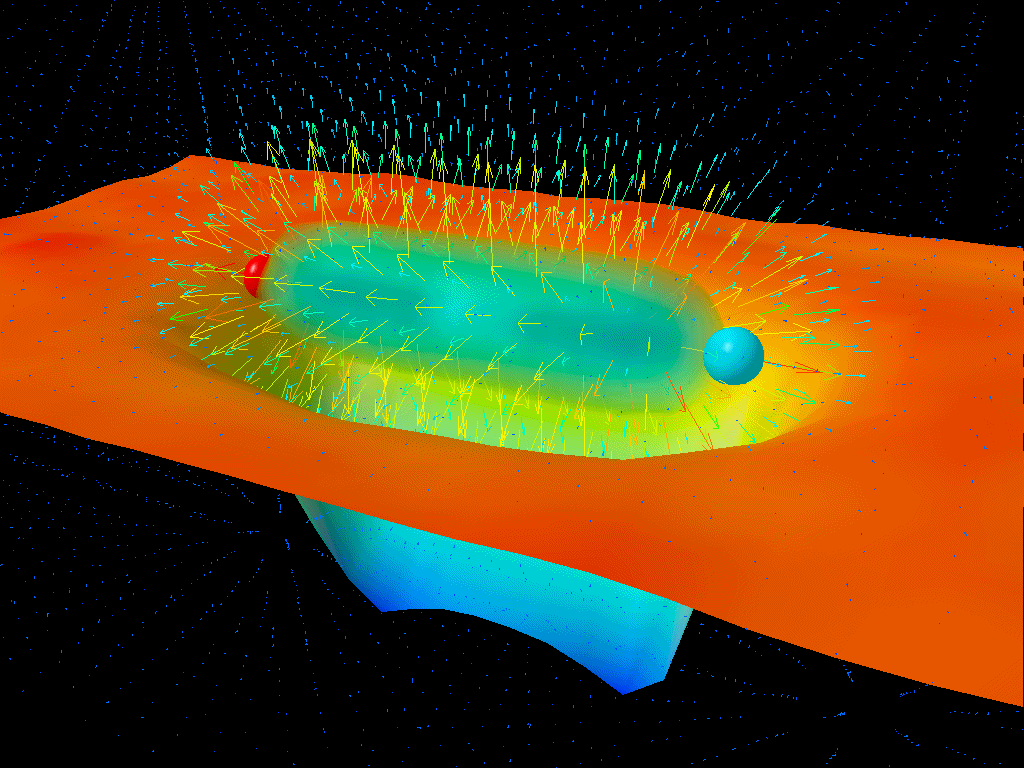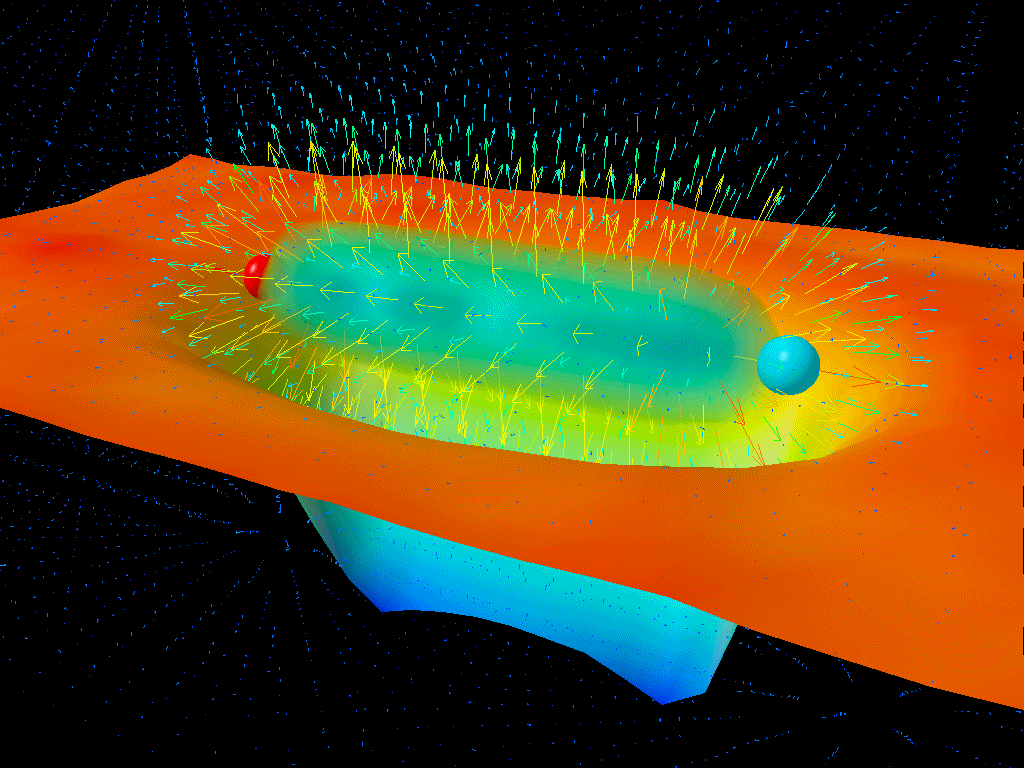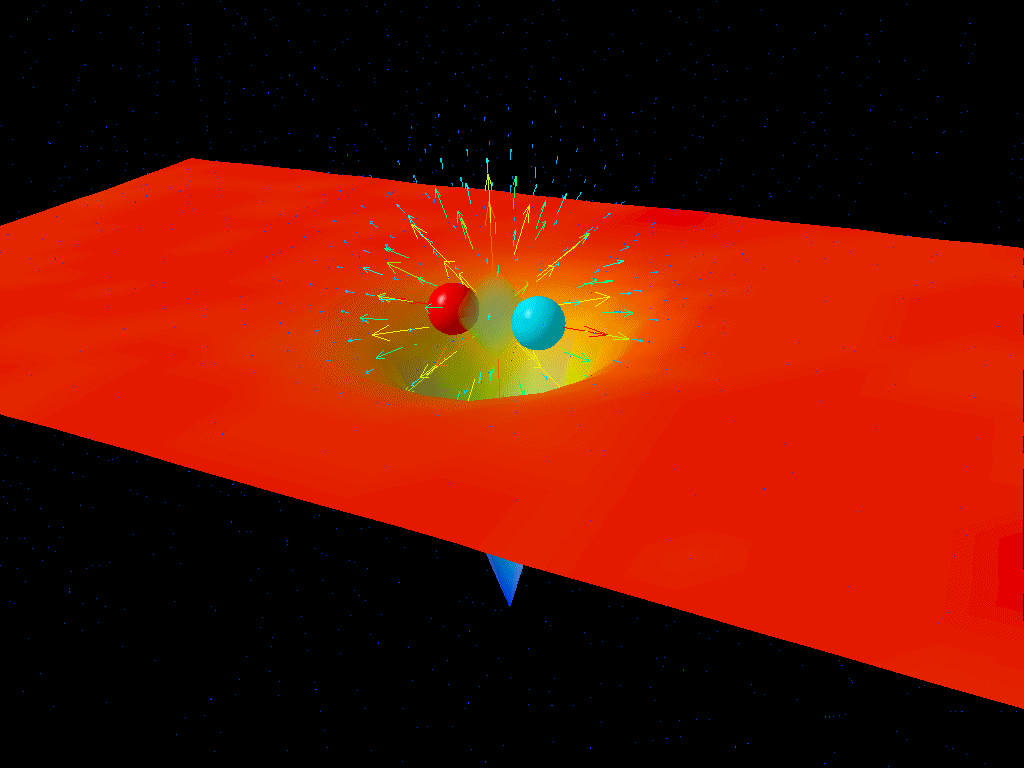
You might think of each electron as generating its own electric (and magnetic, if it’s moving) field. The other electron, then, sees the field(s) generated by the first one, and experiences a force based on the field it’s moving through.
In the context of the quantum Universe, however this already poses a problem. Fields push on particles at a certain position, and then change the particle’s momentum by a certain amount. But in a Universe where position and momentum are mutually uncertain, you can’t simply treat them as though they have a specific, known value. Instead, the fields themselves have to be quantum in nature: behaving as operators, rather than quantities with perfectly determined values.

How do we make a field — something that has a specific “value” at every location in space based on its distance from every source that we have — into something that’s inherently quantum in nature?
We have to promote these fields to become operators: a process known as canonical quantization. (Alternatively, a more modern but equivalent approach is Feynman’s path integral formalism.) If you can create or destroy particles — through matter-antimatter creation and annihilation, radiative processes, or through decays — you need quantum fields to describe things.
The way you do this is to define what we call the vacuum (or lowest-energy, or ground) state: a state with zero particles in it. This is the basis for building all other states, which includes states with one, two, or an arbitrarily large number of particles (or antiparticles) in it. If these particles interact, however, either with one another or simply with the vacuum state itself, the vacuum can become polarized.
Polarization is where you apply a field to something, and the “thing” itself responds to the field. The most common example is a dielectric medium, such as a ceramic. These are useful in all sorts of electrical and electronic applications, because if you apply an external electric field to them, they create their own internal electric field. If you then remove the external field, the internal field goes away.
Well, a novel thing that comes along with quantum field theory — but not in regular quantum mechanics — is that the vacuum itself can become polarized: not just electrically, but under any force or interaction. Even in the absence of charged sources, we can still have vacuum polarization occur due to an external field.
This doesn’t mean that empty space itself is full of particles, but rather that you have quantum mechanical operators, including the “particle creation” and “particle annihilation” operators, acting on the vacuum state continuously. This is often visualized as “particle-antiparticle pairs popping in and out of existence,” but that part is just a calculational tool for visualizing what’s happening on a quantum level within empty space.

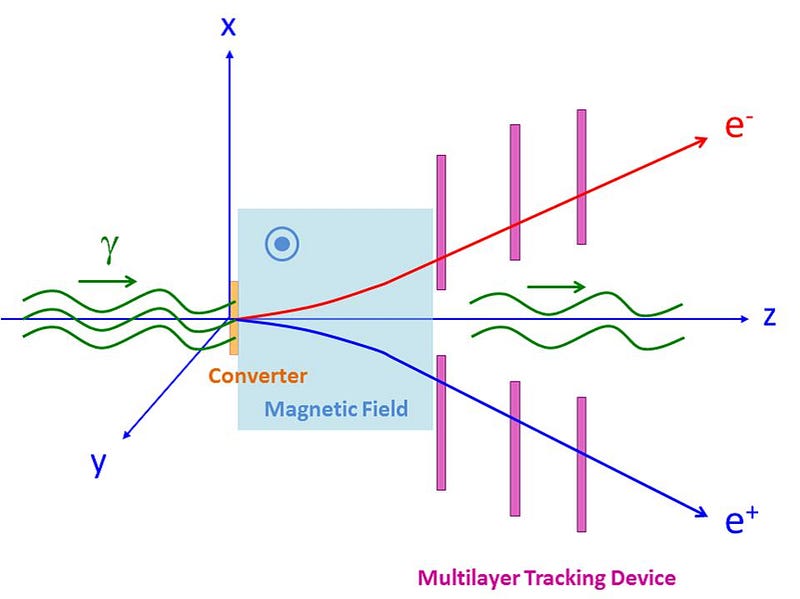
However, this phenomenon does have real, observable effects. One of them is known as vacuum birefringence: the notion that a strong, external field can cause this type of polarization — the creation of an internal field — to empty space itself. For a long time, this was thought to be unobservable, but nature gives us an opportunity where electric and magnetic fields are stronger than anyplace else known: in the immediate vicinity of a neutron star.
Despite what you might think, neutron stars are “only” made of about 90% neutrons; their outer layers are rife with electrons, neutrons, protons, and other atomic nuclei. Rotating at up to about ⅔ the speed of light, these charged particles moving at these speeds create tremendous currents and magnetic fields. When light passes through this region of space where vacuum birefringence occurs, it gets polarized, but only if this phenomenon inherent to quantum field theory is true.
In 2016, this polarization from light around neutron stars was observed for the first time, confirming this picture and an astrophysical prediction that dated back all the way to Heisenberg.
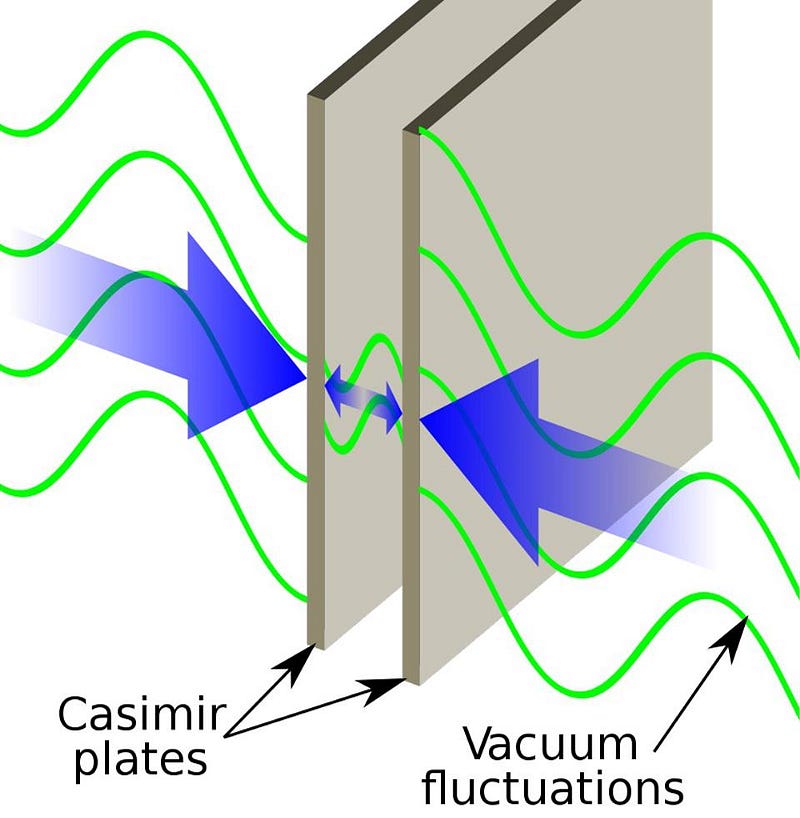
But there’s a second observable effect as well: the Casimir effect. If empty space itself is in this operator-rich state, then the vacuum should be filled with the energetic contributions from all of the possible allowed states. In 1948, Hendrik Casimir had an idea that if you set up the right boundary conditions, you could restrict or forbid certain quantum states for existing within a particular region of space. If the quantum vacuum outside this region doesn’t have any restrictions on it, but the vacuum inside the region does, then there will be a differential force, and the region itself will either contract or expand.
The setup was simple in principle: place two parallel, conducting plates in a vacuum, which restricts the possible states of the electromagnetic vacuum inside the plates, but not outside. Finally, in 1997 — when Casimir himself was 88 years old — physicist Steve Lamoreaux made the first experimental measurement of the Casimir effect, determining that two closely spaced parallel plates did, in fact, attract due to the differences in the quantum vacuum inside and outside the plates. In multiple different ways, theory and experiment agree.
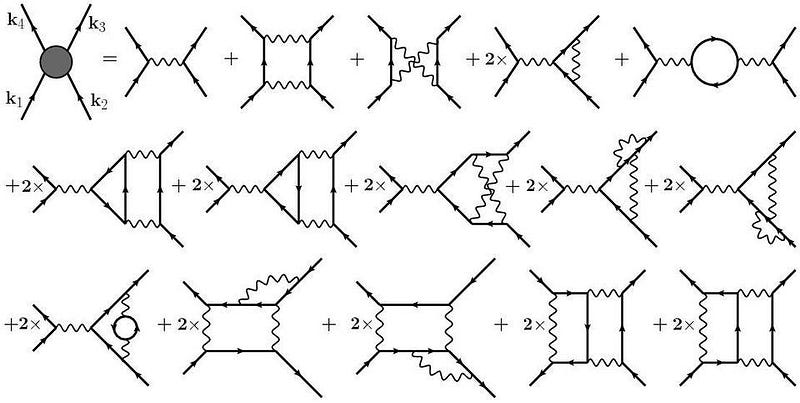
So the quantum vacuum really does have observational effects, and those effects have been observed experimentally on ~micron scales and astrophysically over stellar scales. That doesn’t mean that virtual particles are physically real, however. It means that using the calculational tool of virtual particles in the vacuum allows us to make quantitative predictions about how matter and energy behave as they pass through empty space, and how empty space comes to possess different properties when external fields or boundary conditions are applied. The particles, however, are not real, in the sense that we cannot collide or interact with them.
However, if you have real particles — i.e., a non-vacuum state — then the same quantum field theory techniques you would use to calculate the quantum vacuum actually tells you about real, physical particles (and antiparticles) that can pop in-and-out of existence. For example, we normally think of a proton as being made of three quarks, held together by gluons. But when we perform high-energy collisions of these protons and probe their insides through deep inelastic scattering, we actually find all sorts of extra particles inside: extra quarks and antiquarks, an extreme density of gluons, and even leptons and additional bosons in there. Not only are the effects of virtual particles “real” in particle-rich environments, but the particles themselves are real, too.
In the vacuum of empty space, no matter what boundary conditions you set up or how strong your external fields are, you won’t ever be able to scatter off of whatever’s in the quantum vacuum. However, the quantum vacuum itself will exhibit real, physical effects on matter and radiation that passes through them. The vacuum gets polarized, meaning it generates its own internal fields, and those internal fields — not just the external ones — affect the matter and radiation that passes through. However, there are no particles themselves in there to smash into, collide with, or scatter off of.
The effects of the quantum vacuum are real; the virtual particle visualization is useful, but the particles themselves are not real. Only if you have real particles in your space can the virtual particles arising from particle-field or particle-particle interactions actually be directly detected, indicating their “realness” in some sense. Remember, the only justification we have for calling anything “real” is that we can detect and measure it. The effects of virtual particles are real, but the particles themselves are not!
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.