Ask Ethan: Does The Expanding Universe Break The Speed Of Light?

It’s 92 billion light-years wide after just 13.8 billion years. And that’s just fine.
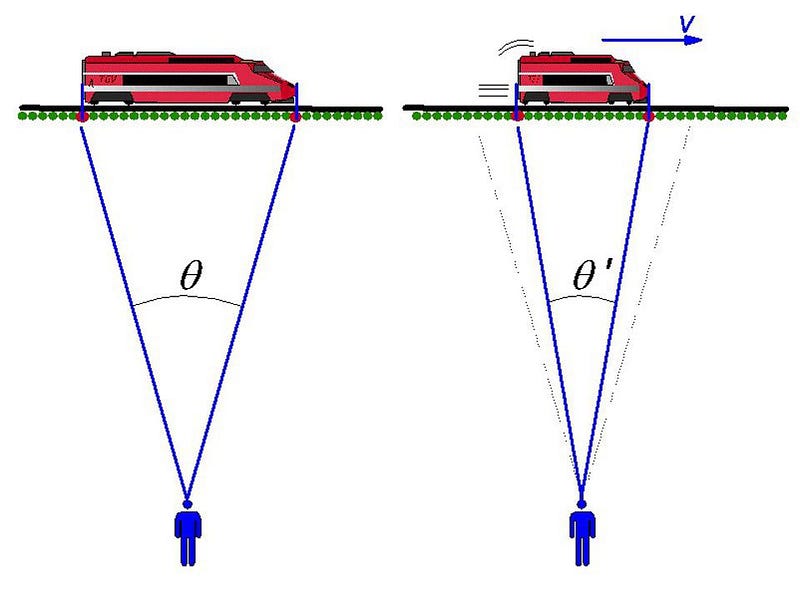
If there’s one rule that people know about how fast things can move, it’s that there’s a cosmic speed limit: the speed of light in a vacuum. If you have any amount of mass at all — like anything made of atoms — you can’t even reach that limit; you can only approach it. Meanwhile, if you have no mass and you’re traveling through completely empty space, there’s no other speed you’re allowed to move at; you must move at the speed of light. And yet, if you think about how big the observable Universe is, we know it’s grown to 92 billion light-years in diameter in just 13.8 billion years. Moreover, by the time just one second elapsed since the Big Bang, the Universe was already multiple light-years across! How is this possible without breaking the laws of physics? That’s what Roberto Cánovas’s son Lucas wants to know, inquiring:
“If the Universe grew more than 300,000 km in a fraction of a second that means all these things had to travel faster than the speed of light during that tiny amount of time thus breaking the rule that nothing can travel faster than light.”
If you want to understand what’s going on, you’re going to have to bend your brain a little bit, because both things are simultaneously true: the Universe really does grow in this fashion, and yet nothing can travel faster than light. Let’s unpack how this happens.

Let’s start with the rule you know: that nothing can travel faster than light. Although this rule is normally attributed to Einstein — it’s a cornerstone of Special Relativity — it was actually known, or at least strongly suspected, to be true for more than a decade before him.
If you have an object at rest, and you apply a force to it, it’s going to accelerate. That’s Newton’s famous F = ma, which says that force equals mass times acceleration. If you apply a force to any massive object, it’s going to accelerate, which means it’s going to speed up in a particular direction.
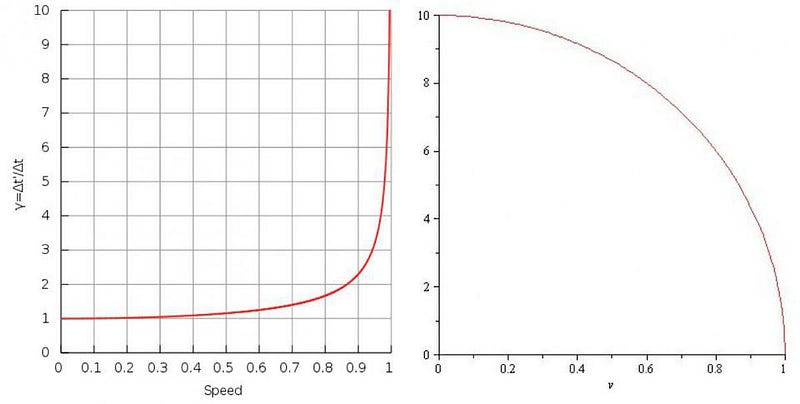
But that can’t be strictly true all the time. Imagine you accelerate something so that it gets faster by 1 kilometer-per-second with each second that goes by. If you start from rest, it would only take 299,793 seconds (about 3½ days) before you reached and then exceeded the speed of light! Instead, there must be different rules at play when you get near that speed, and we figured out those rules back in the late 1800s, back when Einstein was still a child.
People like George FitzGerald and Hendrik Lorentz, working in the 19th century, derived something spectacular: that when you got close to the speed of light, the Universe you observed appeared to play by different rules. Normally, we’re used to a ruler being a good way to measure distances, and clocks being a good way to measure time. If you were to take your ruler and measure a moving object, you’d expect to measure the same value as if the object were stationary, or if someone on board that object used their own ruler. Similarly, if you used your watch to measure how much time elapsed between two events while someone on the moving object used theirs, you’d expect that everyone would get the same results.
But you don’t get the same results! If you, at rest, measure the length of the moving object, you’d see it was shorter: lengths contract when you move, and they contract by more when you get close to the speed of light.
Similarly, if you, at rest, measured how fast the person in motion’s clock was going, you’d see their clock running slower compared to yours. We call these two phenomena “length contraction” and “time dilation,” and they were discovered back when Einstein was just a small child.
So what did Einstein do that was so important? His spectacular realization was that, no matter whether you’re stationary or you’re on that moving object, when you look at a beam of light, you’re always going to see it moving at the same speed. Imagine you shine a flashlight pointed away from you. If you’re stationary, light moves at the speed of light, and your clock runs at its normal speed with your ruler reading its normal length. But what happens if you’re in motion, straight ahead, and you shine that flashlight in front of you?
From someone stationary’s perspective, they’ll see light moving away from you at a slower speed: whatever your speed is subtracted from the speed of light. But they’d also see that you’re compressed in the direction that you’re moving: your distances and your rulers have contracted. Additionally, they’ll see your clocks running slower.
And these effects combine in such a way that, if you’re the one moving, you’ll see that your rulers appear normal, your clocks appear normal, and light moves away from you at the speed of light. All of these effects exactly cancel out for all observers; everyone in the Universe, regardless of how you’re moving, sees light move at exactly the same speed: the speed of light.
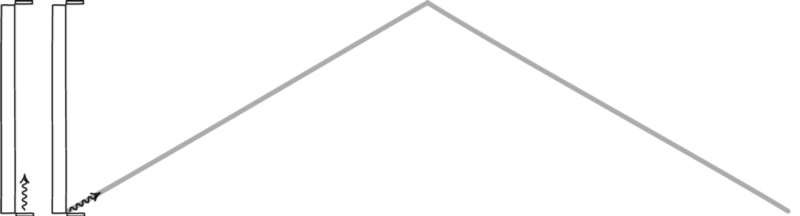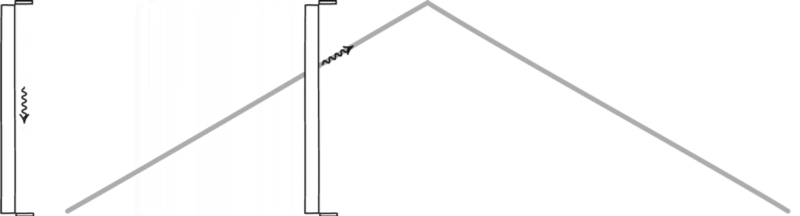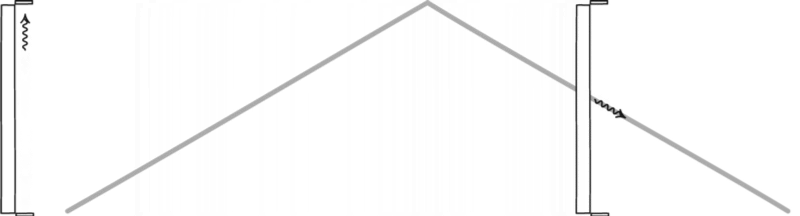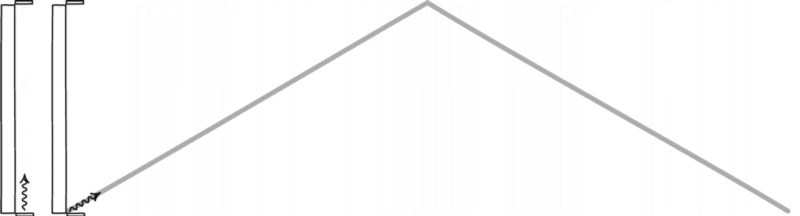
This has a terrific consequence: it means that the equation F = ma isn’t right when we talk about relativity! If you were moving at 99% the speed of light, and you applied a force that theoretically would accelerate you that extra 1% of the way there, you wouldn’t reach 100% the speed of light. In fact, you’d find that you’re only going 99.02% the speed of light. Even though you applied a force that should accelerate you by 1% the speed of light, because you’re already moving at 99% the speed of light, it only increases your speed by 0.02% the speed of light instead.
What’s happening is that, instead of going into your speed, that force is changing your momentum and your kinetic energy, not according to Newton’s classic laws, but according to the laws of relativity. Time dilation and length contraction come along for the ride, and it’s why unstable, short-lived particles that live for minuscule amounts of time can travel farther than non-relativistic physics can account for. If you hold out your hand, you’ll find that one unstable cosmic particle — a muon — passes through it each second. Even though these are created by cosmic rays more than 100 kilometers up, and the muon’s lifetime is only 2.2 microseconds, these particles can actually make it all the way down to Earth’s surface, despite the fact that 2.2 microseconds at the speed of light won’t even take you 1 kilometer.

All of this analysis, though, was for Einstein’s Special Relativity. In our Universe, particularly on cosmic scales, we have to use General Relativity.
What’s the difference?
They’re both theories of relativity: where your motion through space is relative to your motion through time, and everyone who has a different position and velocity has their own unique frame of reference. But Special Relativity is a “special, specific case” of General Relativity. In Special Relativity, there are no gravitational effects. There are no masses curving space; there are no gravitational waves passing through your location; there is no expansion or contraction of the Universe allowed. Space, for lack of a better term, is flat, rather than curved.
But in General Relativity, not only is space allowed to be curved, but if you have any masses or any forms of energy in your Universe at all, it must be curved. The presence of matter and energy tells space how to curve, and that curved space tells matter and energy how to move. We’ve detected the effects of this curvature — around the Sun, around Earth, and even in the great cosmic laboratory of outer space — and it always seems to agree with Einstein’s (and General Relativity’s) predictions.

In every case, where we were talking about things being limited by the speed of light, we were talking about a special case: about objects moving around and (possibly) accelerating through space, but where space itself wasn’t fundamentally changing. In a Universe where the only type of relativity is Special Relativity, this is fine. But we live in a Universe that’s full of matter and energy, and where gravitation is real. We can’t use Special Relativity except as an approximation: where things like the curvature of space and the expansion of the Universe are negligible. That might be fine here on Earth, but it’s not fine when it comes to the expanding Universe.
Here’s the difference. Imagine that your Universe is a ball of dough, and that there are raisins located all throughout it. In Special Relativity, the raisins can all move through the dough a little bit: all limited by the speed of light and the laws of relativity (and relative motion) that you’re familiar with. No raisin moves through the dough faster than the speed of light, and and two raisins will calculate and measure their relative speeds to be below the speed of light.
But now, in General Relativity, there’s one major difference: the dough itself can expand.
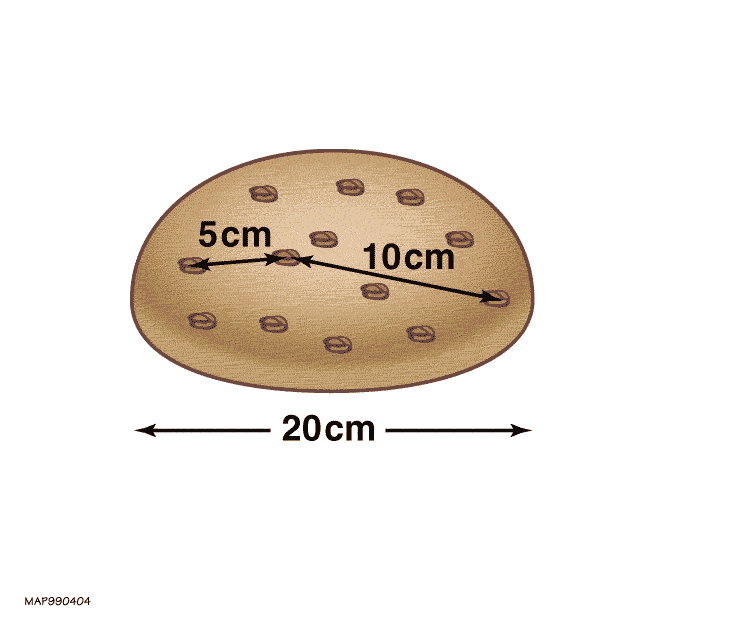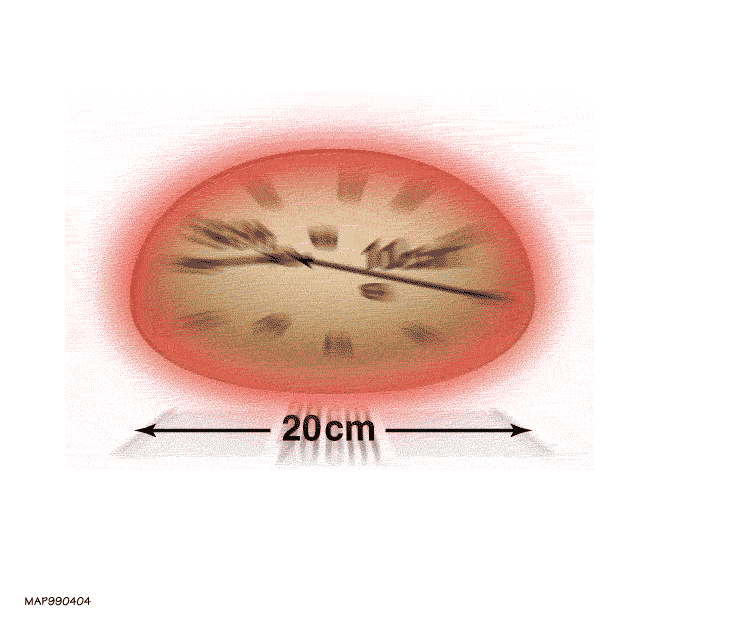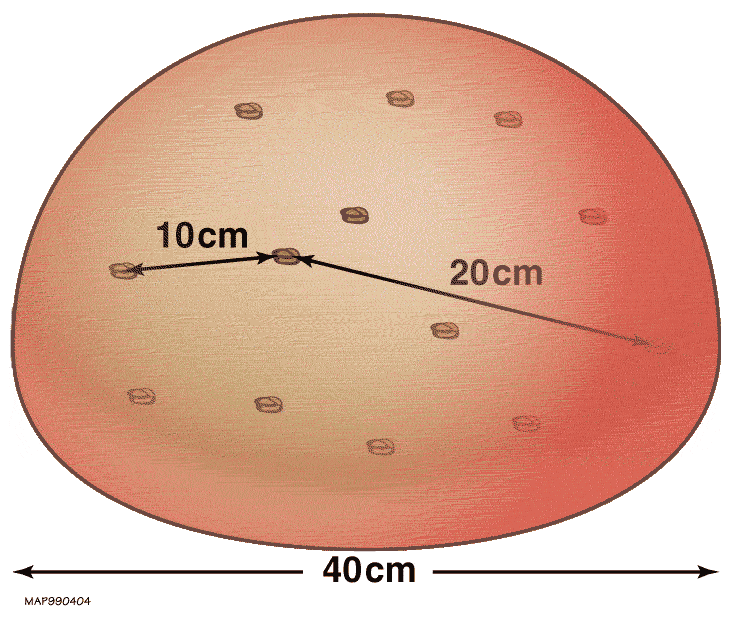
The dough isn’t something you can observe, detect, or measure; it’s simply the nothingness of empty space. But even this nothingness has physical properties. It determines what distances are, what trajectories objects will follow, how time flows, and many other properties. All you can see, though, are the individual particles and waves — the quanta of energy — that exist in what we call “spacetime.” Spacetime itself is the dough; the particles in the dough, from atoms to galaxies, are like the raisins.
Now, this dough is expanding, just like you’d imagine a ball of dough would expand if you left it to leaven in a place with no gravity, like aboard the International Space Station. As the dough expands, any particular raisin can represent you, the observer.
The raisins that are close by you will appear to expand away from you slowly; the ones that are far away will appear to expand away from you quickly. But in reality, this isn’t because the raisins are moving through space; it’s because space itself is expanding, and the raisins themselves only move through that space slower than light.

It also means that it takes a long time for the light coming from those objects to arrive at our eyes; the farther away we look, we see objects as they were earlier and earlier in the Universe’s history. There’s actually a limit to how far away we can see, because the Big Bang occurred a finite amount of time ago, 13.8 billion years ago, to be precise. If the Universe hadn’t expanded at all — if we lived in a Special Relativity Universe instead of a General Relativity Universe — we’d only be able to see 13.8 billion light-years in all directions, for a diameter of ~27.6 billion light-years.
But our Universe is expanding, and has been expanding for all that time. It actually expanded faster in the past, because there was more matter-and-energy in a given region of space before the Universe expanded by such a great amount. With the combination we have of matter, radiation, and dark energy in our Universe, the light that’s arriving today comes to us after a 13.8 billion year journey, but those objects are now 46 billion light-years away. The Universe didn’t expand faster than light, though; every object in the Universe always moved at or below the speed of light. It’s just that the fabric of space itself — what you might consider “nothing” to be — expands between the numerous galaxies.
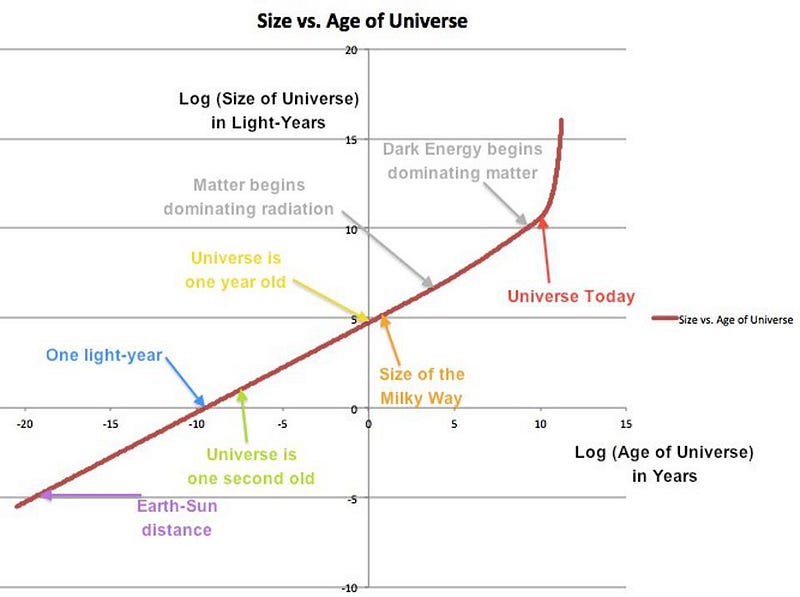
It’s very hard to think about a Universe where space itself is changing over time. Conventionally, we look out at an object in the Universe and measure it with the tools and techniques we have here at our disposal. We’re used to interpreting certain measurements in a specific way. Measure how faint something looks or how small it appears, and based on its actual brightness or known size, you can say, “it must be this distance away.” Measure how its light has shifted from when it was emitted to when we observe it, and you can say, “this is how fast it’s receding from us.” And if you look at the different objects at different distances, you’ll notice that an object more than 18 billion light-years away will never have the light its emitting right now reach us, as the Universe’s expansion will prevent it from reaching us, even at the speed of light.
Our first instinct is to say nothing can travel faster than light, meaning that no object can move through space faster than the speed that light can move through a vacuum. But it’s also correct to say, “nothing can travel faster than light,” as the fabric of empty space — nothingness itself — possesses neither a limit to the rate of its expansion nor a limit to the distances over which the expansion applies. The Universe grew to be about 50 light-years in size by the time it was just 1 second old, and yet not a single particle in that Universe traveled through space faster than light. The nothingness of space simply expanded, and that’s the simplest and most consistent explanation for what we observe.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.





