Ask Ethan: How Can A Nuclear Bomb Be Hotter Than The Center Of Our Sun?

The center of our Sun tops out at 15 million K, but nuclear bombs can get nearly 20 times hotter. Here’s how.

In terms of raw energy output, nothing on our world compares to our Sun. Deep inside our Sun, nuclear fusion transform enormous quantities of hydrogen into helium, producing energy in the process. Every second, this fusion causes the Sun to burn through 700 million tons of fuel, much of which gets converted into energy via Einstein’s E = mc². Nothing on Earth can compare to this amount of energy. But in terms of temperature, we’ve got the Sun beat. That puzzles Paul Dean, who asks:

[T]he temperature in the core of our sun is usually cited at 15 million degrees Celsius or so. […] What I don’t get is this: some mid-sized thermonuclear test detonations done by the old Soviet Union and the USA have been recorded at (if only very briefly) 200 or even 300 million degrees Celsius. How can our pithy 3 stage hydrogen bomb blasts be so much hotter than the dense hell of the Sun’s monster fusion oven?

It’s a great question with a fascinating answer. Let’s find out.

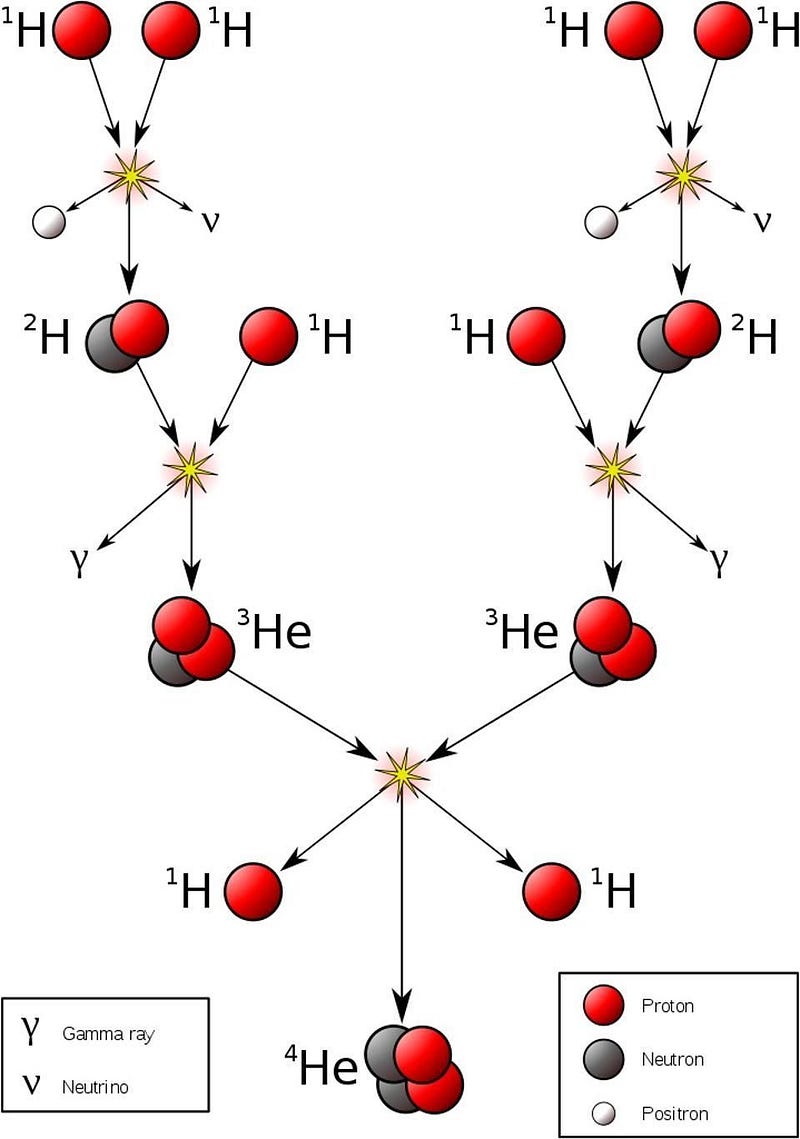
The most powerful nuclear detonations on Earth and the interior of the Sun actually have a lot in common.

1. They both get the overwhelming majority of their energy from nuclear fusion: compressing light nuclei into heavier ones.
2. The process of fusion is energetically favorable, meaning that the products are lower in mass than the reactants.
3. This mass difference means that the “missing mass” gets converted into energy via Einstein’s famous equation, E = mc².
4. And this process, for as long as it endures, injects a tremendous amount of energy into a confined volume of space.

The physics that governs these nuclear reactions are the same regardless of where they take place: whether inside the Sun or in the critical core region of an atomic bomb explosion.

The hottest part of any explosion occurs in the initial stages, when the majority of the energy gets released but remains in a very small volume of space. For the early, single-stage atomic bombs we had on Earth, that meant the initial detonation was where the highest temperatures occurred. Even a few fractions-of-a-second afterwards, the rapid, adiabatic expansion of the gas inside causes the temperature to drop dramatically.

But in a multi-stage atomic bomb, a small fission bomb is placed around material that’s suitable for nuclear fusion. The nuclear explosion compresses and heats the material inside, achieving the high temperatures and densities necessary to ignite that runaway nuclear reaction. When nuclear fusion occurs, even greater amounts of energy are released, epitomized by the Soviet Union’s 1960 detonation of the Tsar Bomba.

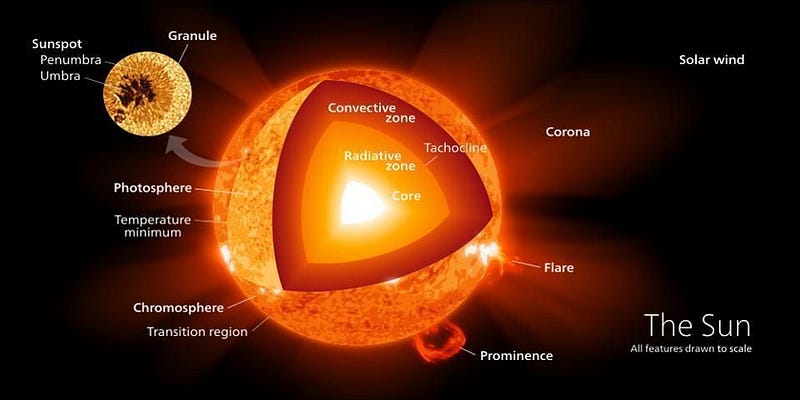
It’s true: the hottest hydrogen bombs, leveraging the power of nuclear fusion, have indeed achieved temperatures of hundreds of millions of degrees Celsius. (Or kelvin, whose units we’ll use from now on.) By contrast, inside the Sun, the temperature is a relatively cool ~6,000 K at the edge of the photosphere, but rises as you travel down towards the Sun’s core through the various layers.

The majority of the Sun’s volume is composed of the radiative zone, where temperatures increase from the thousands into the millions of K. At some critical location, temperatures rise past a threshold of around 4 million K, which is the energy threshold necessary for nuclear fusion to begin. As you go closer towards the center, the temperature rises and rises, to a peak of 15 million K in the very center. This is the hottest temperature achieved in a star like our Sun.

“How,” you might wonder, “can a miniature version of the Sun that only ignites for a fraction of a second reach higher temperatures than the very center of the Sun?”

And it’s a reasonable question to ask. If you look at total energy, there’s no comparison. The aforementioned Tsar Bomba, the largest nuclear explosion ever to take place on Earth, gave off the equivalent of 50 megatons of TNT: 210 petajoules of energy. On the other hand, the overwhelming majority of the Sun’s energy comes from the hottest regions; 99% of the Sun’s energy output comes from regions at 10 million K or hotter, despite the fact that such a region makes up only a small percentage of the core’s volume. The Sun emits the equivalent of 4 × 10²⁶ J of energy each second, by comparison, some 2 billion times more energy than the Tsar Bomba gave off.

With such enormous differences in energy, it might seem like a mistake to conclude that an atomic bomb’s temperature is many times higher than the center of the Sun. And yet, it isn’t all about energy. It’s not even about power, or the energy released in a given amount of time; the Sun has the atomic bomb beaten by a wide margin in that metric as well. Neither energy nor energy-per-unit-time can successfully explain why atomic bombs can reach higher temperatures than the Sun’s core.

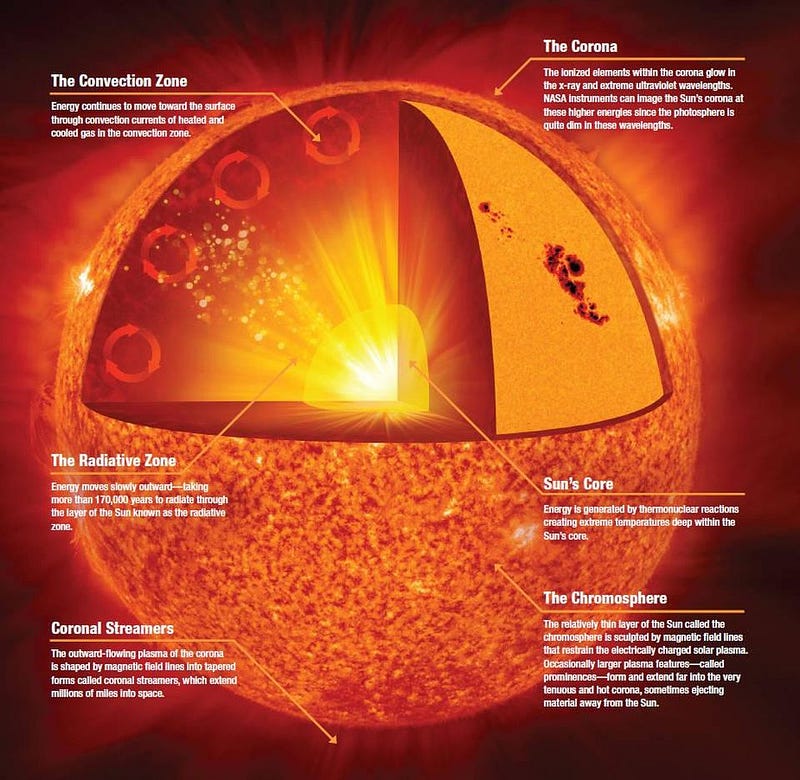
But there is a physical explanation, and the way to see it for yourself is to think about the volume of the Sun. Yes, there’s an enormous amount of energy being emitted, but the Sun is huge. If we restrict ourselves to the core, even to the innermost, hottest region of the core, we’re still talking about enormous volumes of space, and that makes all the difference.

The majority of fusion occurs in the innermost 20–25% of the Sun, by radius. But that’s only about 1% of the Sun, by volume. Because the Sun is so enormous — its diameter is approximately 1,400,000 kilometers, or over 100 times the diameter of Earth — the total amount of energy and power it produces is spread out over an enormous volume. The key thing to look at isn’t just mass, energy, or power, but the density of those quantities.

For the very core of the Sun, where all of those quantities are at their highest, the Sun has:

• a density of 150 grams-per-cubic-centimeter, about 150 times the density of water,
• a power density of about 300 watts-per-cubic-meter, about the same power output as a warm-blooded human’s body heat,
• and an energy density, as a result, that corresponds to a temperature of 15 million K.

Over the volume of space that the Sun’s core comprises, that makes up a literally astronomical amount of mass, energy, and power. But in any particular region of space, the rate of fusion is relatively slow. Giving off 300 W of power per cubic meter is about the same amount of power that you give off throughout the day in terms of heat energy, burning through your chemical-based fuel to maintain your warm-blooded body temperature.

In terms of the amount of nuclear fusion per unit volume, that’s merely the equivalent of converting about 3 femtograms of mass (3 × 10^–18 kg) into energy each second for each cubic meter of space inside the Sun’s core. For comparison, the Tsar Bomba — whose explosion all occurred in a fraction-of-a-second within a volume less than one cubic meter — converted more than 2 kg of mass (about 5 pounds’ worth) into pure energy.

That’s the most important realization when it comes to understanding how a terrestrial nuclear explosion can reach higher temperatures, particularly over a very short time interval, than the hottest part of our Sun can. By almost every meaningful metric, the Sun far outclasses anything we can create on Earth, including mass, energy, volume, power, and the sustained output of what is produced.

But there are a few small but important ways that a nuclear explosion defeats the Sun. In particular:

• the number of fusion reactions in a given amount of (small) volume is much greater,
• these reactions take place over a much shorter amount of time on Earth than in the Sun,
• and therefore, the total amount of energy released per unit volume is much larger.

For a very small amount of time, until adiabatic expansion causes the volume of the explosion to increase and the temperature to drop, a nuclear explosion can out-heat even the center of the Sun.

The interior of the Sun is one of the most extreme places we can imagine. At temperatures of 15 million K and matter compressed to densities 150 times as great as liquid water on Earth, it’s hot and dense enough for nuclear fusion to proceed continuously, outputting 300 J of energy each second for every cubic meter of space. It’s a reaction that’s relentless and continuous, like a wood-fired oven except hotter, denser, and running on nuclear fuel.

But a multi-stage hydrogen bomb, where a fission bomb causes the inner core to compress, achieving higher densities from the compression than even at the Sun’s center. When the fusion reaction begins, those nuclear processes occurring at those extraordinary densities can lead to a chain reaction so powerful that, for a brief moment, the amount of heat-per-particle in a given volume exceeds that of the Sun. That’s how, here on Earth, we can produce something — albeit just for an instant — that truly is hotter than even the center of the Sun.

Send in your Ask Ethan questions to startswithabang at gmail dot com!