Ask Ethan: How Long Do We Have Until We Need To Change Our Calendar?
Leap years will only get us through the next few thousand years before we have to fix it.
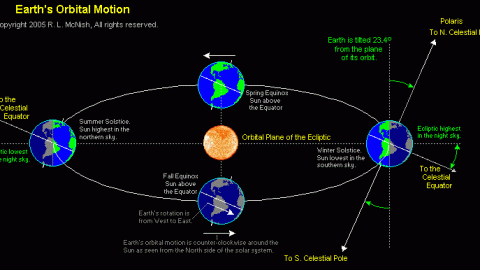
With every year that passes, we assume that two separate things will both line up. One is the seasonal year on Earth: the progression from winter to spring to summer to fall and back around again, coinciding with the periodic solstices and equinoxes as well. On the other hand, there’s also the astronomical year: where the Earth completes a full revolution around the Sun and returns to the same point in its orbit. The whole point of switching to the calendar we now use — the Gregorian Calendar — was to make sure that these two ways of tracking the passage of a year, using the Tropical Year (which aligns with the seasons) rather than the Sidereal Year (which aligns with Earth’s orbit).
But even by choosing the Tropical year, our calendar won’t in fact, always line up, even with our modern knowledge of timekeeping. That’s because the orbital properties of Earth itself are changing over time, and once enough time passes, we’ll have to modify our calendar to keep up. But how long do we have, and how will we need to modify it? That’s what Alisa Rothe wants to know, asking:
“[I read that] the Earth is slowing down in its orbit around the Sun. Does this mean that we will eventually have to add another day to our calendar year? How much time will pass before that becomes necessary? And in the same way, did a year used to contain fewer days 4.5 billion years ago?”
These are great questions. But to find out the answers, we have to look at all the changes that are happening together, to see which ones matter the most.

Let’s start by answering a simpler question: right now, how good is the matchup between the “calendar year” and the actual Tropical Year?
The Tropical Year is the same whether you measure it from:
- summer solstice to summer solstice,
- winter solstice to winter solstice,
- spring equinox to spring equinox,
- autumnal equinox to autumnal equinox,
or any other point in time, based on the Sun’s position in the sky relative to Earth, as it was the year before. To calculate the tropical year, you have to fold in not just Earth spinning on its axis and revolving around the Sun, but also the precession of the equinoxes and all other orbital changes.
Basically, if you took a look at Earth’s axis and said, “this is how it’s oriented, with respect to the Sun, right at this moment,” a single Tropical Year would mark the very next time that the Earth’s axis returned to that exact same orientation. It’s not quite the same as a 360° revolution around the Sun, but off by a small amount. In terms of the amount of time it takes to make up one Tropical Year today, it’s precisely 365.2422 days. In more conventional terms, that’s 365 days, 5 hours, 48 minutes, and 45 seconds.
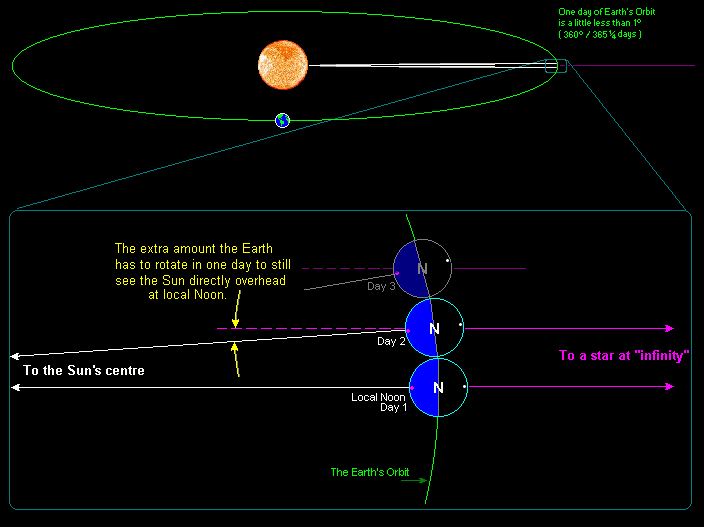
The fact that our Tropical Year isn’t perfectly divisible into a whole number of days is the reason for our relatively complex system of leap years: years where we do (or don’t) insert an extra day into our calendar. Most years, we assign 365 days to our calendar, while on leap years, we add in a 366th day: February 29th.
Originally, we kept time using the Julian Calendar, which added that 366th day in every four years: on a leap year. This led to a long-term estimate of 365.25 days in a year, meaning that for every four years that passed on our calendar, we were moving out-of-sync with the actual Tropical Year by 45 minutes.
By the time the 16th century came around, we were out of sync with the actual year by more than an actual week. As a result, by decree in 1582, when the Gregorian calendar was introduced, the days between October 5 and October 14 were simply skipped on the calendar, bringing the calendar year and the Tropical Year back into alignment. When you hear stories like, “Isaac Newton was born on Christmas” or that Shakespeare and Cervantes both died on the same day, don’t be fooled. England was decades late in adopting this calendar switch; according to the calendar we use today, Newton was born in January and Shakespeare lived an additional 10 days after the death of Cervantes.
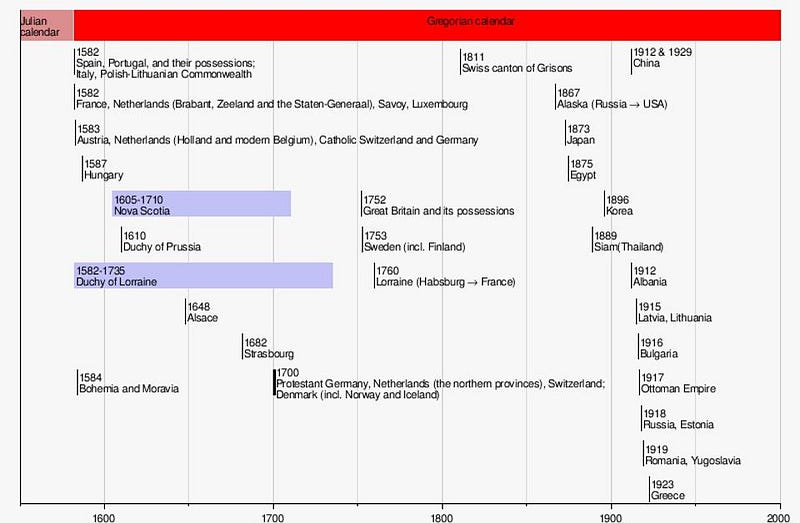
The difference is that, according to the Gregorian calendar, we don’t have a leap year every four years; we have a leap year every four years except on years ending in “00” that aren’t also divisible by 400. In other words, 2000 was a leap year, but 1900 and 1800 weren’t, and 2100 won’t be, either. This translates into a long-term average of 365.2425 days in a year, which only pulls us out of sync from the true Tropical Year by about 27 seconds with every passing year.
That’s pretty good! That means we could wait an additional 3200 years before the Gregorian calendar went out-of-sync with the Tropical Year by even a single day; a remarkable accuracy for how we keep time. In fact, if we modified the Gregorian calendar to exempt every year that was also divisible by 3200 from being a leap year, it would take some ~700,000 years before our calendar were off by a single day!
But all of this assumes two things, neither one of which is actually true.
- That Earth, spinning on its axis, will always take the same amount of time to complete a full 360° rotation as it does today.
- And that the Earth, revolving around the Sun, will always follow the same precise orbit that it follows today.
If we want to know how our calendar needs to be modified over time, we have to take into account all of the changes that will occur over time — quantitatively — and combine them all together. Only then can we know how our Tropical Year will change over time, and that will inform what we need to do to keep our calendar synchronized with the year as we experience it on Earth.
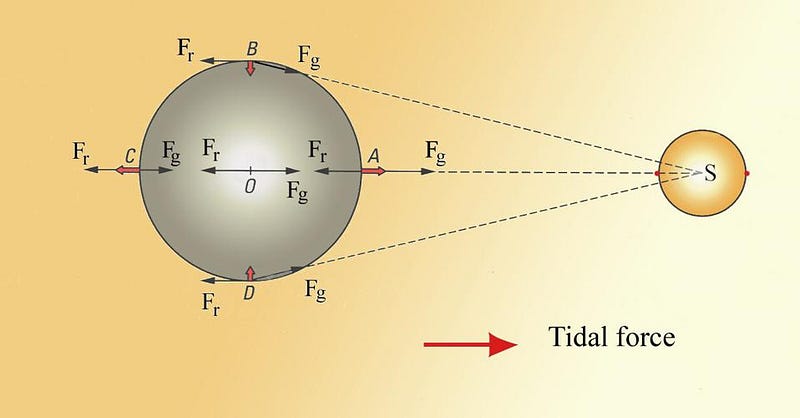
Whenever you have one mass pulling on another, you’re going to not only see the effects of gravitational attraction at play, but also the effects of tidal forces. You can think of tides as arising from the fact that whenever you have an object that takes up volume — like planet Earth — one side of it is always going to be “closer” to the attracting mass than the center, while the opposite side is “farther” from the attracting mass. The closer portions experience a greater gravitational force, while the more distant portions experience a lesser force.
Similarly, parts of the mass that are above or below, as well as on either lateral side, will experience their force in a slightly different direction. When the Sun and Moon act on the Earth, our planet bulges a little bit due to these tidal forces. And, when something gravitationally pulls on a spinning, bulging object, that external force acts the same way that lightly putting your finger up against a spinning top acts: as a frictional force, slowing the rotation down. Over time, this can really add up!
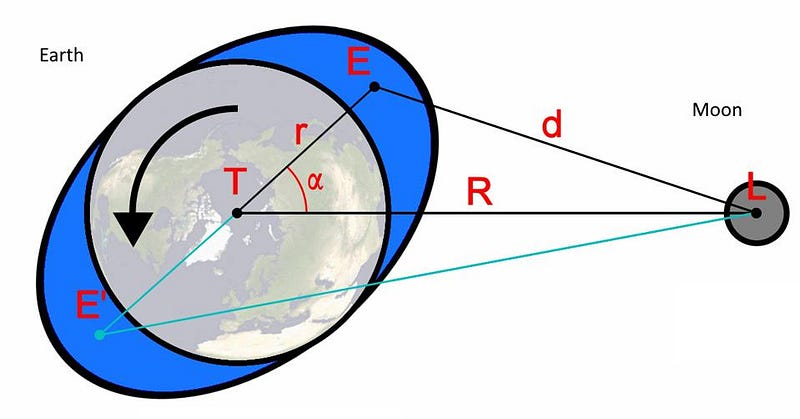
This “braking” effect takes angular momentum away from the spinning Earth, causing it to rotate slower and slower over time. But angular momentum is something that’s fundamentally conserved; it cannot be created or destroyed, only transferred from one object to another. If the Earth’s rotation is slowing down, that angular momentum must transfer elsewhere.
So where is that elsewhere? Into the Moon, which spirals away from the Earth as the Earth’s rotation slows down.
With every year that passes, these tidal forces lengthen the amount of time it takes for Earth to complete a full 360° rotation by a tiny, but barely perceptible amount. Compared to precisely one year ago today, our planet takes an extra 14 microseconds to complete a full rotation. This extra 14 microseconds per day adds up over time, which is why — on average — we have to add a leap second to our clock to keep them where they ought to be every 18 months.
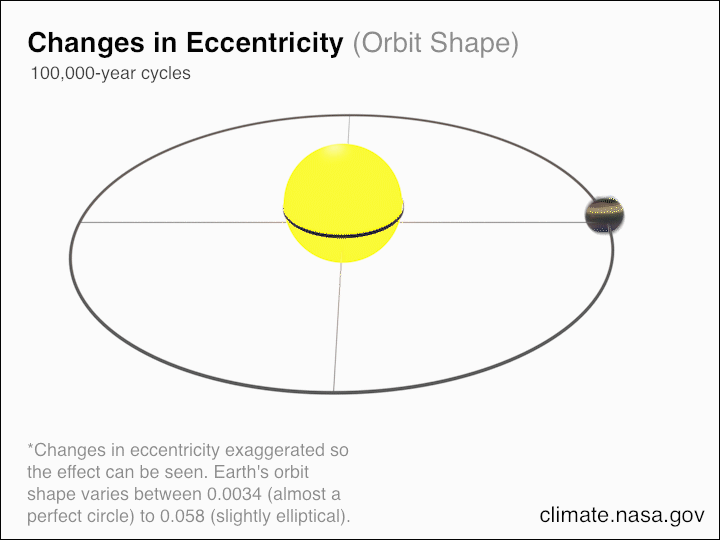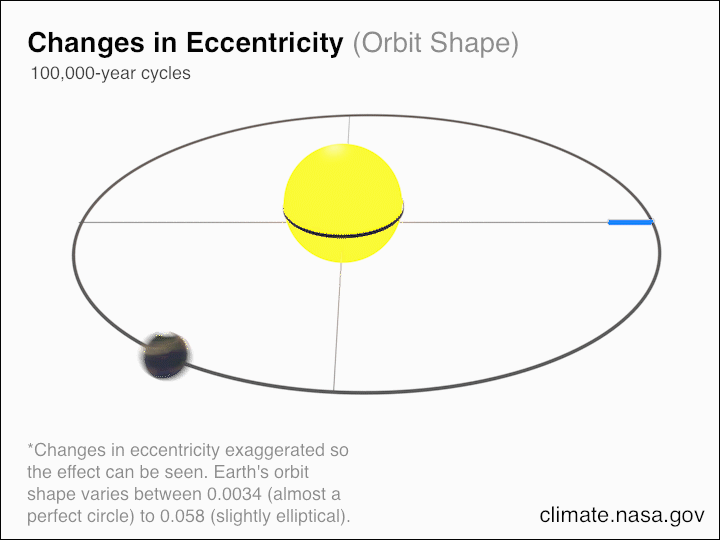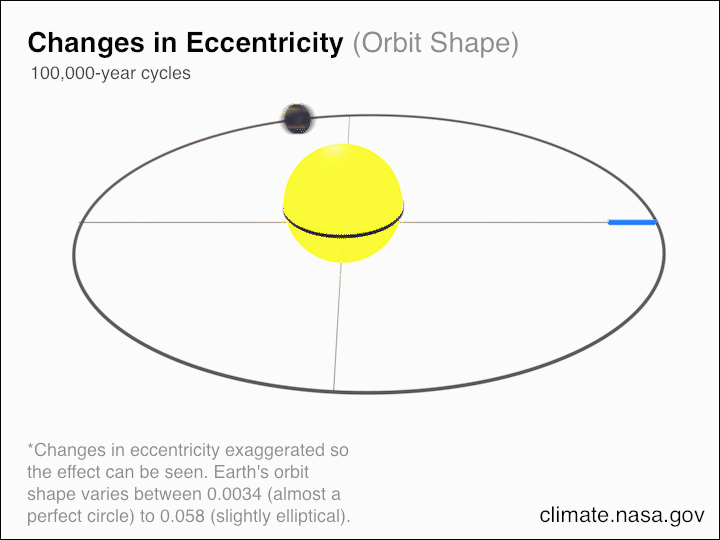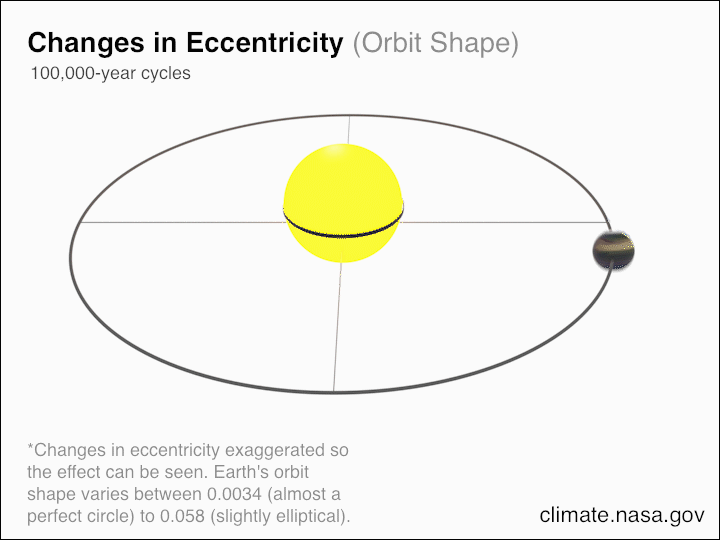
Of course, this effect accumulates over longer periods of time, but there are other effects working alongside it:
- radiation from the Sun, which pushes Earth slightly outward in its orbit around the Sun,
- the solar wind — particles from the Sun — which collide with Earth and slightly slow its motion down,
- and mass loss from the Sun, which emits particles and converts mass into energy (via Einstein’s E = mc²) through nuclear fusion in its core, causing Earth to slowly spiral outwards, away from the Sun.
While the effects of angular momentum loss cause Earth to spin at a slower rate, meaning that as time goes on, it takes fewer “days” to make up a year, these effects all do something else entirely. When you push Earth outwards, when you slow Earth’s motion down, or when you decrease the mass of the Sun, it causes the year to lengthen. The greatest effect, as it turns out, comes from mass loss, as the Sun a total of about 5.6 million tons of mass each second from nuclear fusion (4 million) and the solar wind (1.6 million) combined, or the equivalent of 177 trillion tons of mass per year.

With each year that goes by, this mass loss means that Earth spirals outwards at a rate of approximately 1.5 cm (about 0.6 inches) every year. Over the history of our Solar System, taking into account how our Sun has changed, we’re somewhere around 50,000 km farther from the Sun versus 4.5 billion years ago. And we’re orbiting around the Sun at a slightly slower speed — about 0.01 km/s slower — today than we were back when the Solar System first formed.
Consider that at our fastest, Earth moves through space at 30.29 km/s (18.83 mi/s), while at our slowest, we move at 29.29 km/s (18.20 mi/s), this difference is very, very small, and the effect can be completely neglected without losing pretty much any accuracy. Similarly, effects like earthquakes, ice melting, core formation, and thermal expansion of the Earth all exist, but only dominate on very short timescales where changes are relatively rapid.
What does, then, on the long timescales we’re considering? The dominant effect in determining how the length of a Tropical Year changes relative to a calendar year is set by tidal braking of the Earth. And the longer we wait, the greater the discrepancy becomes. It won’t be, astronomically speaking, all that long before adding a second here or there becomes a wildly insufficient fix for our changing planet.
The way we’ll need to modify our calendar, as the Earth’s rotation slightly slows down, is by removing days, rather than adding them. As time goes on initially, we’ll want to begin reducing the frequency of leap years; we’ll be able to eliminate them entirely after another ~4 million years passes. At that point, Earth will rotate a little more slowly, and a calendar year will correspond to precisely 365.0000 days. Beyond that point, we’ll need to start having “reverse” leap years, where we remove a day every so often, before we eventually go down to ~364 day years some ~21 million years into the future. As these changes occur, the day will lengthen to greater than 24 hours. Eventually, we’ll even pass Mars, with a 24 hour, 37 minute day, to become the planet with the 3rd longest day in the Solar System, behind only Mercury and Venus.
It might lead you to question: does this mean we had more days — and shorter days — back earlier in the Earth’s history?
Not only do we think this is the case, but we have evidence supporting it! Geologically, the oceans rise and fall along continental coasts with the tides, and always have. Daily patterns can get permanently “baked” into the soil, creating formations known as tidal rhythmites. Some of these tidal rhythmites, like the Touchet formation, below, have been preserved in Earth’s sedimentary rock, enabling us to determine our planet’s rotation period in the past. Back when the asteroid that wiped out the dinosaurs struck, 65 million years ago, a day was about 10–15 minutes shorter than it is today. The most ancient such formation comes to us from 620 million years ago, indicating a day that was a little shorter than 22 hours. For as long as we have records, Earth’s day has been lengthening, while the number of days in a year has been dropping.

When we extrapolate back to when the Earth-Moon system formed — and we fold in the uncertainties related to the distribution of mass in the Earth’s interior — a startling picture emerges. Some 4.5 billion years ago, back in the infancy of the Solar System, Earth was completing a full 360° rotation in just 6-to-8 hours. The Moon used to be much closer; back during the first ~3.5 billion years of the Solar System, all solar eclipses were total; annual eclipses have emerged relatively recently. (And, in another 620 million years, they’ll all be annular from then on.) With such a fast spin at the inception of the Earth-Moon system, there would have been over 1000 days in every Earth year, with triple to quadruple the number of sunsets and sunrises compared to what we have now.
What we can’t speak sensibly about, however, is what a day might have been like on proto-Earth back before the great impact occurred that caused the formation of the Moon. The year was probably similar, but we have no way of knowing how quickly our planet was rotating. No matter how much information we gather, there are some pieces of knowledge that have been permanently erased by the damaging events of our natural history. In the Solar System, no matter how much we might hope otherwise, we can only learn about our past from the incomplete information of the survivors.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.





