At Last, Physicists Understand Where Matter’s Mass Comes From

The answer has nothing at all to do with the Higgs boson.

In this Universe, there are very few fundamental properties that cannot be derived from something simpler. The rules governing biological systems are rooted in chemical interactions, bonds, and applied voltages. The rules of chemistry can be derived from more fundamental physical laws that govern all particles. And if you strip down the components of any physical system, you’ll eventually arrive at the simplest descriptions of reality we know of: the particles and interactions that make up all of our known reality. While all the particles that exist have their own specific, unique properties, there are only a few that define them, such as mass, electric charge, color charge, and weak hypercharge. Yet why the particles have the properties they do is not fully understood; the values of the fundamental constants behind the Universe cannot be derived from anything presently known.

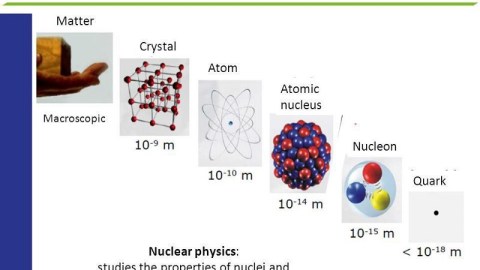
For thousands of years, humanity has searched for the smallest, most fundamental building blocks of nature. Since ancient times, we conjectured that there would be some smallest, uncuttable entities that composed everything in existence. The Greek word ἄτομος, where we get our word “atom” from, literally means indivisible, and yet atoms themselves can be broken up further: into protons, neutrons, and electrons. The electrons are truly uncuttable, but protons and neutrons can be broken up further: into quarks and gluons.

Only here do we arrive at the truly indivisible particles that make up the majority of mass in the world. The particles of the Standard Model — and the ways they bind together — take us to our deepest understanding of reality.

Yet if we take a look at the proton (made of two up and one down quark) and the neutron (made of one up and two down quarks), a puzzle emerges. The three quarks within a proton or neutron, even when you add them all up, comprise less than 0.2% of the known masses of these composite particles. The gluons themselves are massless, while the electrons are less than 0.06% of a proton’s mass. The whole of matter, somehow, weighs much, much more than the sum of its parts.

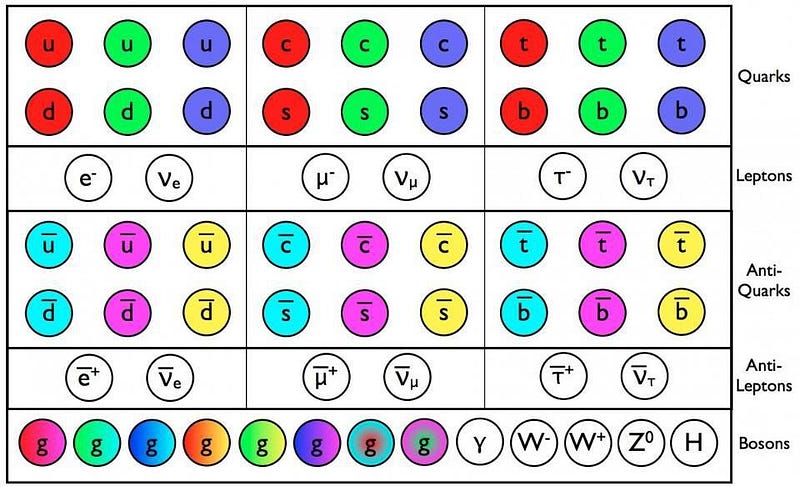
The Higgs may be responsible for the rest mass of these fundamental constituents of matter, but the whole of a single atom is nearly 100 times heavier than the sum of everything known to make it up. The reason has to do with a force that’s very counterintuitive to us: the strong nuclear force. Instead of one type of charge (like gravity, which is always attractive) or two types (the “+” and “-” charges of electromagnetism), the strong force has three color charges (red, green and blue), where the sum of all three charges is colorless.

Furthermore, there are three anti-colors: cyan (anti-red), magenta (anti-green) and yellow (anti-blue), and any color-anticolor combination is also colorless. This is why you can have baryons (made of 3 quarks) or mesons (made of quark/antiquark combinations): because nature needs your complete, bound object to be colorless.

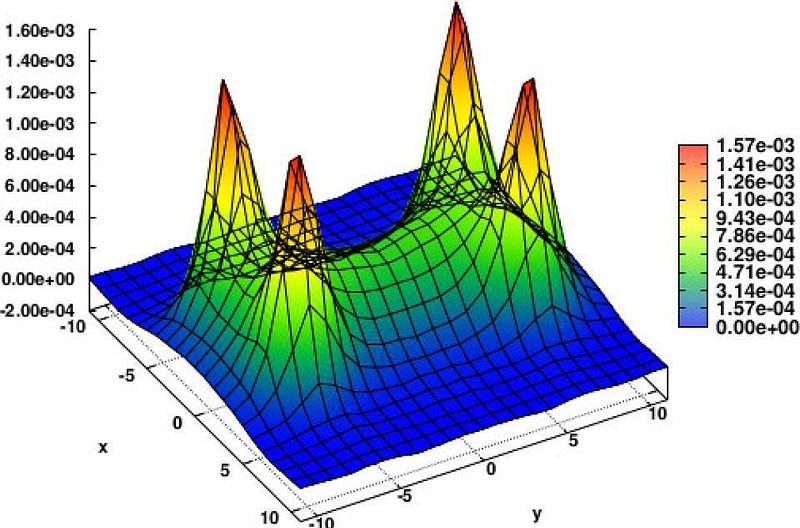
The way quarks bind into protons is fundamentally different from all the other forces and interactions we know of. Instead of the force getting stronger when objects get closer — like the gravitational, electric or magnetic forces — the attractive force goes down to zero when quarks get arbitrarily close. And instead of the force getting weaker when objects get farther away, the force pulling quarks back together gets stronger the farther away they get.

This property of the strong nuclear force is known as asymptotic freedom, and the particles that mediate this force are known as gluons. Somehow, the energy binding the proton together, the other 99.8% of the proton’s mass, comes from these gluons.

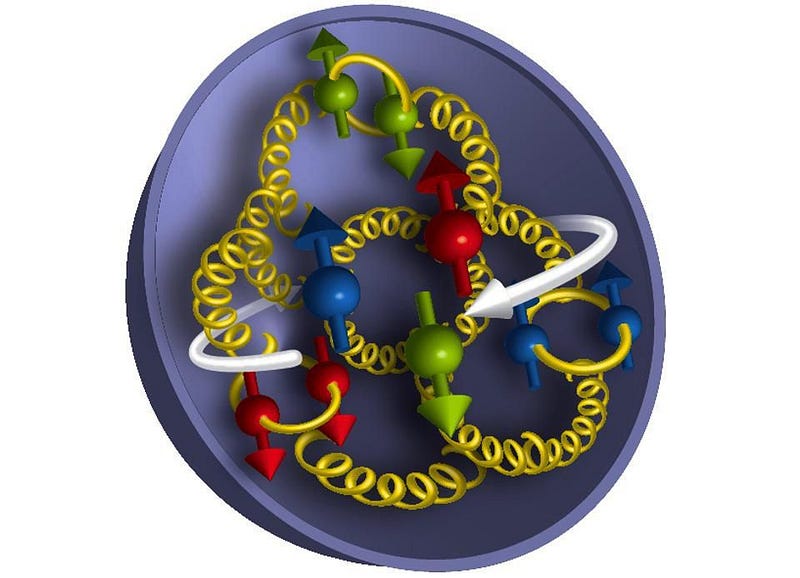
Because of how the strong nuclear force works, there are large uncertainties as to where these gluons are actually located at any point in time. We presently have a solid model of the average gluon density inside a proton, but we need better experimental data and more informed models to know where they are at any particular time.

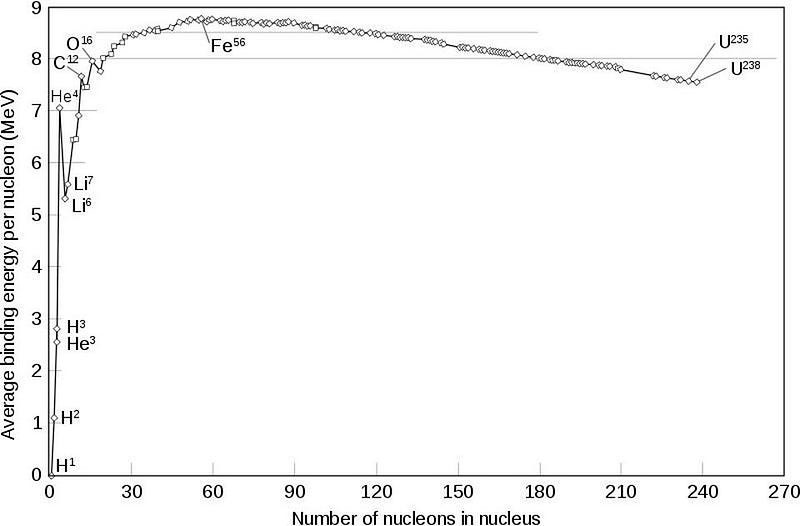
But even with all the things we don’t know, one puzzle is finally yielding: how to calculate the expected mass of not just the proton, but of all atomic nuclei, based on the quark content alone. The strong nuclear force is responsible for a slew of incredible properties of nature, including:

• how protons and neutrons bind together to make atomic nuclei,
• why different elements have different mass-per-nucleon ratios,
• how and at what rate nuclear reactions in the Sun occur,
• and why iron, nickel and cobalt are the most stable elements.

The difficult part with the quantum field theory that describes the strong force — quantum chromodynamics (QCD) — is that the standard approach we take to doing calculations is no good. Typically, we’d look at the effects of particle couplings: the charged quarks exchange a gluon and that mediates the force. They could exchange gluons in a way that creates a particle-antiparticle pair or an additional gluon, and that should be a correction to a simple one-gluon exchange. They could create additional pairs or gluons, which would be higher-order corrections.

We call this approach taking a perturbative expansion in quantum field theory, with the idea that calculating higher and higher-order contributions will give us a more accurate result.

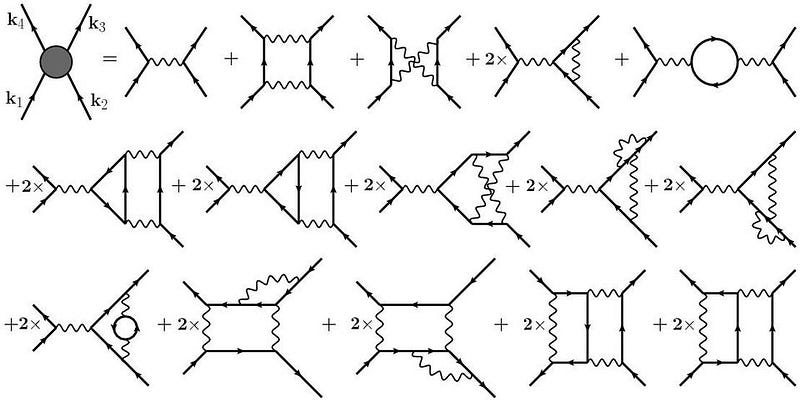
But this approach, which works so well for quantum electrodynamics (QED), fails spectacularly for QCD. The strong force works differently, and so these corrections get very large very quickly. Adding more terms, instead of converging towards the correct answer, diverges and takes you away from it.

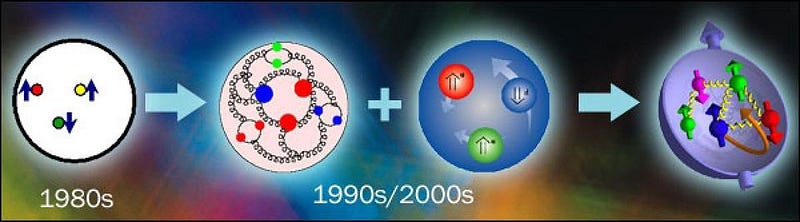
Fortunately, there is another way to approach the problem: non-perturbatively, using a technique called Lattice QCD. By treating space and time as a grid (or lattice of points) rather than a continuum, where the lattice is arbitrarily large and the spacing is arbitrarily small, you overcome this problem in a clever way. Whereas in standard, perturbative QCD, the continuous nature of space means that you lose the ability to calculate interaction strengths at small distances, the lattice approach means there’s a cutoff at the size of the lattice spacing. Quarks exist at the intersections of grid lines; gluons exist along the links connecting grid points.

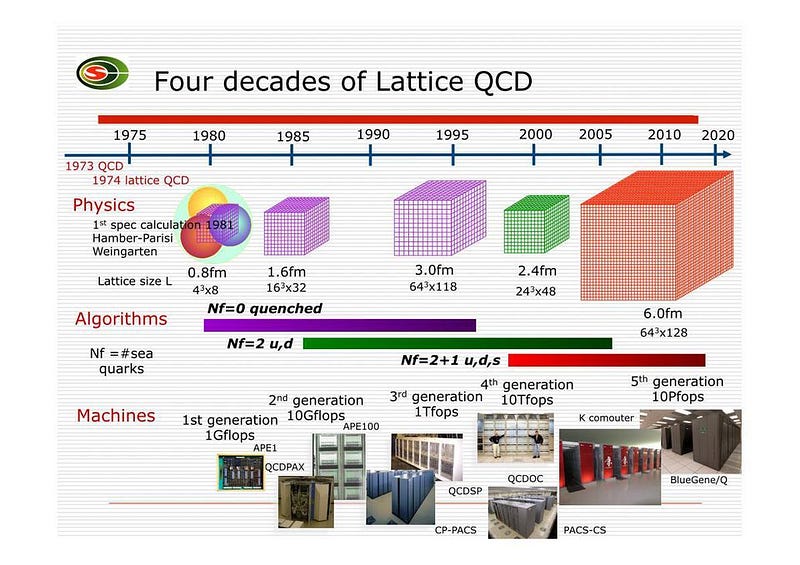
So long as you have enough computing power, you can recover the predictions of QCD to whatever precision you like, simply by making the lattice spacing smaller, which costs more in terms of computational power but improves your calculational accuracy. Over the past three decades, this technique has led to an explosion of solid predictions, including the masses of light nuclei and the reaction rates of fusion under specific temperature and energy conditions. The mass of the proton, from first principles, can now be theoretically predicted to within 2%.

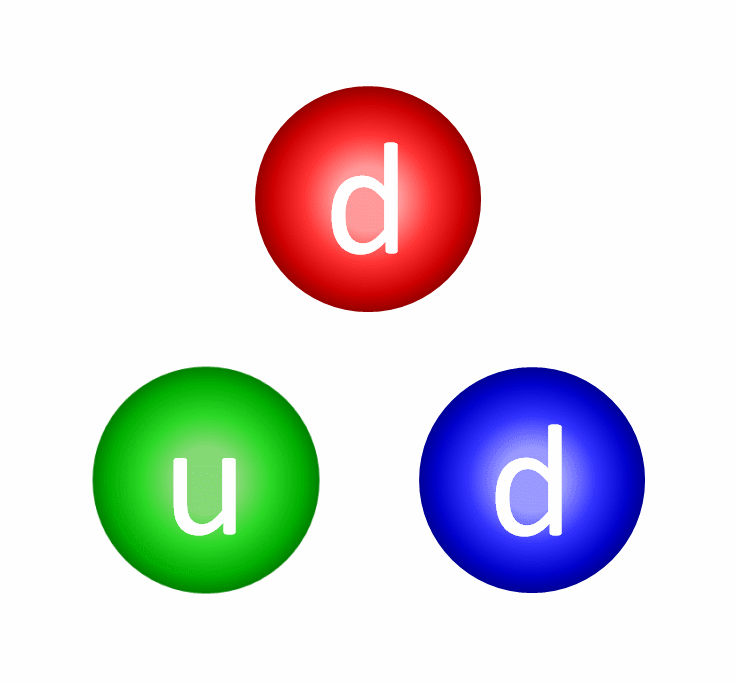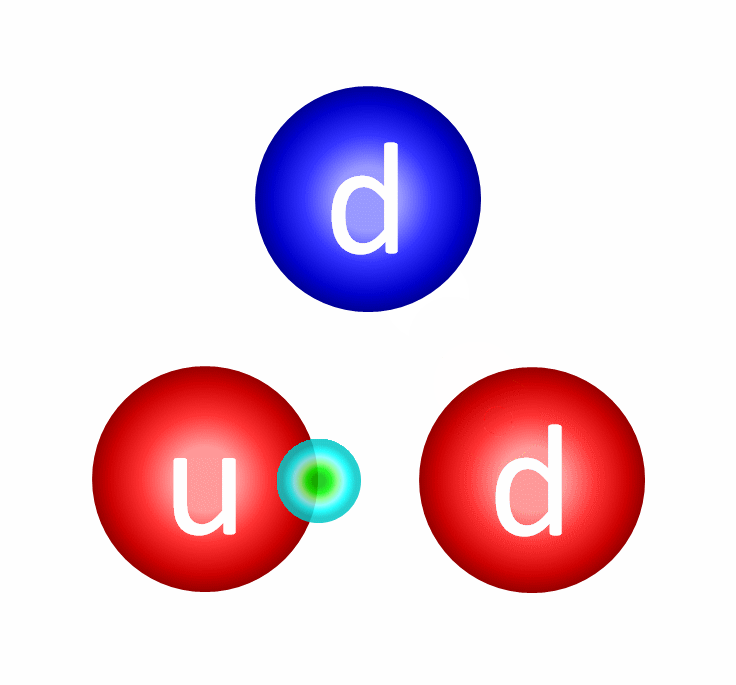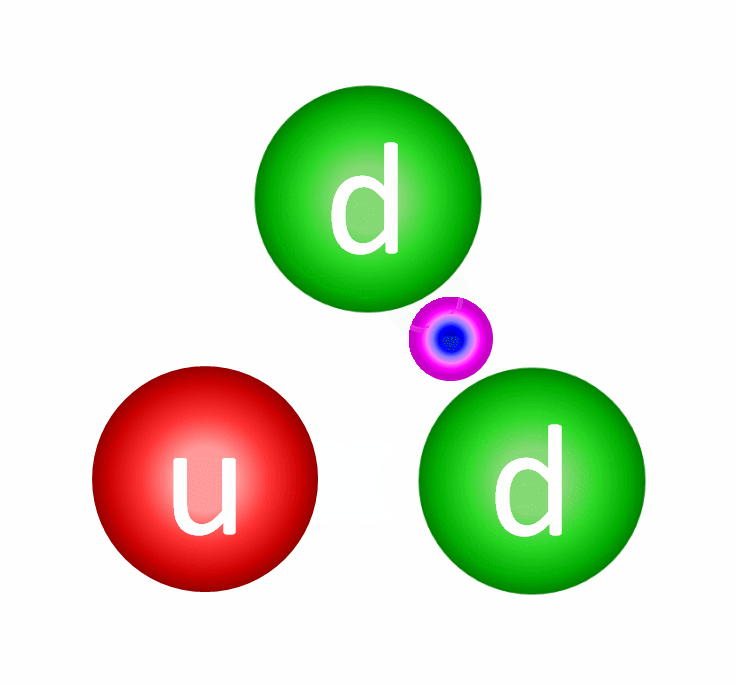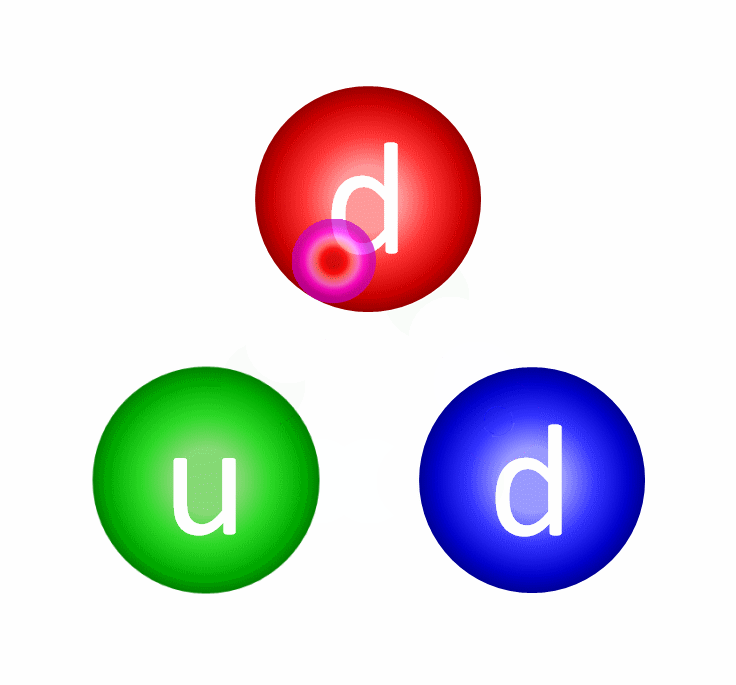
Lattice QCD is not only teaching us how the strong interactions lead to the overwhelming majority of the mass of normal matter in our Universe, but holds the potential to teach us about all sorts of other phenomena, from nuclear reactions to dark matter.

Later today, November 7th, physics professor Phiala Shanahan will be delivering a public lecture from Perimeter Institute, and we’ll be live-blogging it right here at 7 PM ET / 4 PM PT. You can watch the talk right here, and follow along with my commentary below. Shanahan is an expert in theoretical nuclear and particle physics and specializes in supercomputer work involving QCD, and I’m so curious what else she has to say.

Tune in tonight to find out!

(Live blog to run below beginning at 3:50 PM; all times in bold given in the Pacific timezone.)

3:50 PM: Alright! We’re here, and we’re ready to get started. Before we do, though, some of you might be wondering just why we need Lattice QCD, and how this differs from a standard calculation that you would perform in any other quantum field theory. After all, standard QFT techniques are well-known, well-understood, and based on Feynman diagrams. You may have seen them before.

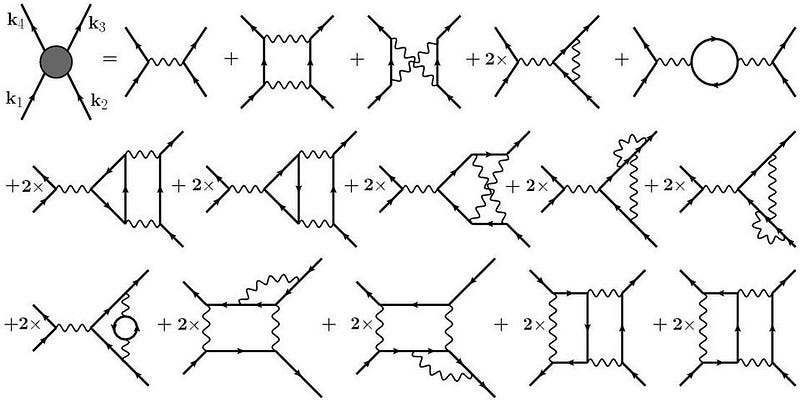
3:54 PM: The way that these diagrams work is that they help you, once you compute their contributions, calculate a contribution to the overall effect you’re trying to understand. How strong is an electron-photon scattering interaction? How strong is a quark-gluon interaction? The approach is to add up progressively more-and-more terms with more-and-more loops, vertices, and particles, getting closer-and-closer to the actual answer.

3:57 PM: But there’s a limit to the accuracy you can reach. You’re used to mathematical series that converge, like 1/2 + 1/4 + 1/8 + 1/16… and so on. This series converges to 1, and if you add up an infinite number of terms, that’s the answer.

But there’s also another type of series that could either converge or diverge: an asymptotic series, like a/2 + b/4 + c/8 + d/16… and so on, where the letter could be any constants at all. In some cases, your series will converge; in others, they will diverge. In quantum field theories like QED, they diverge, but only after like 1,000 terms. But in QCD, the theory of the strong interaction, they start to diverge super quickly, like on term #2.

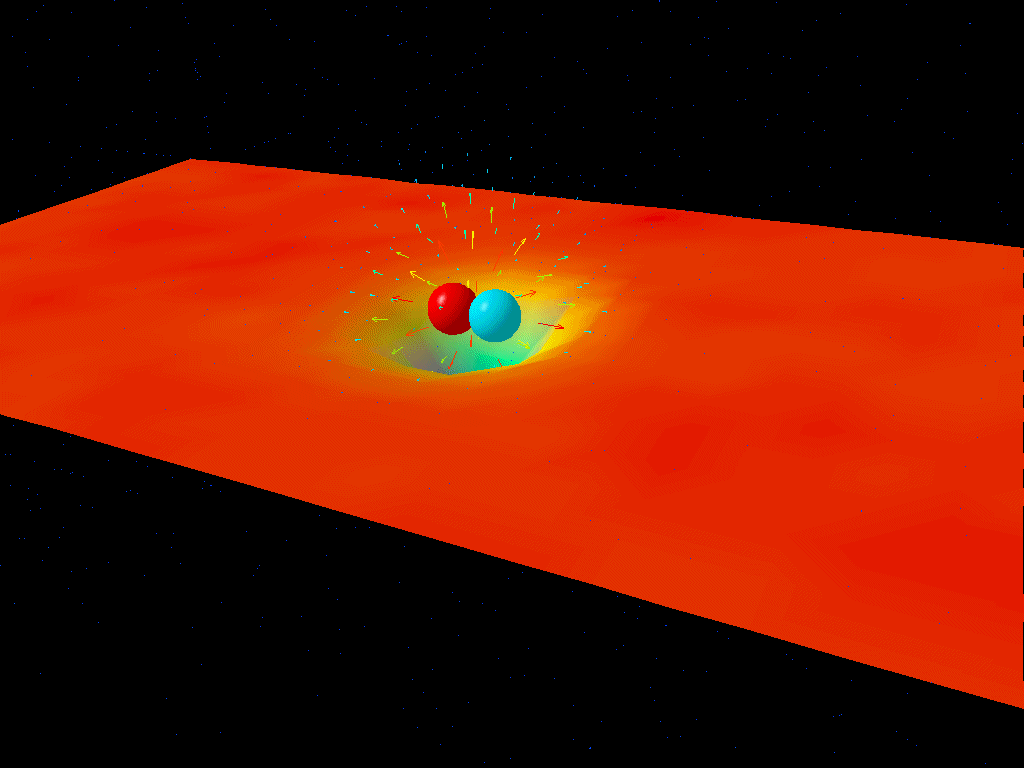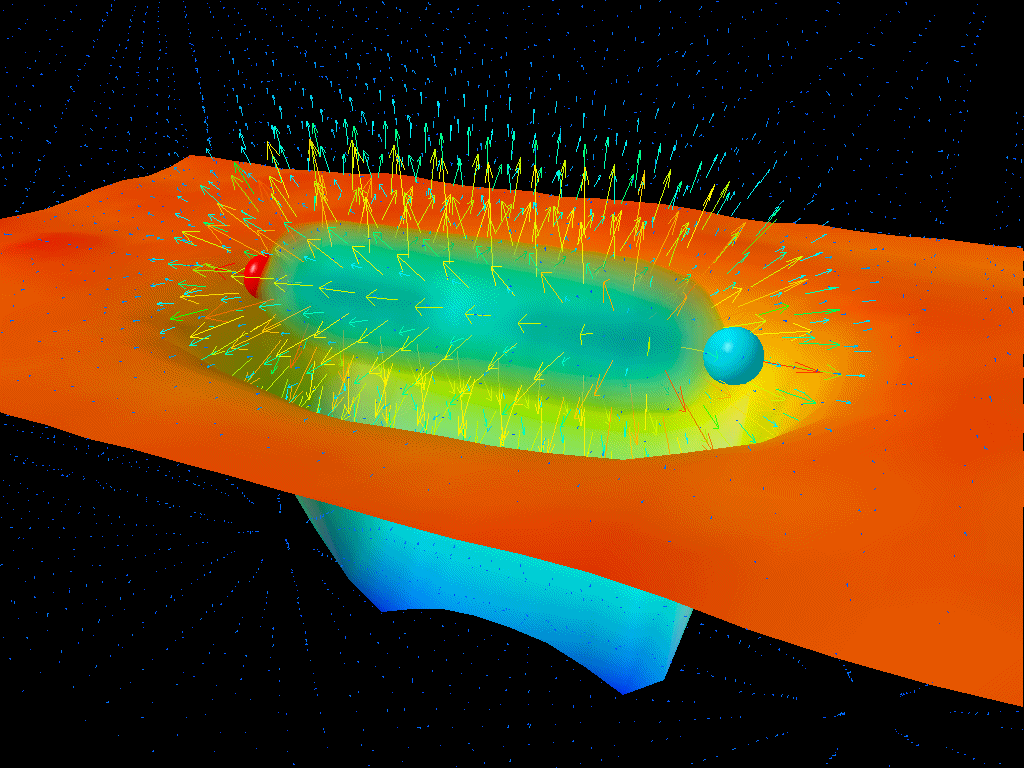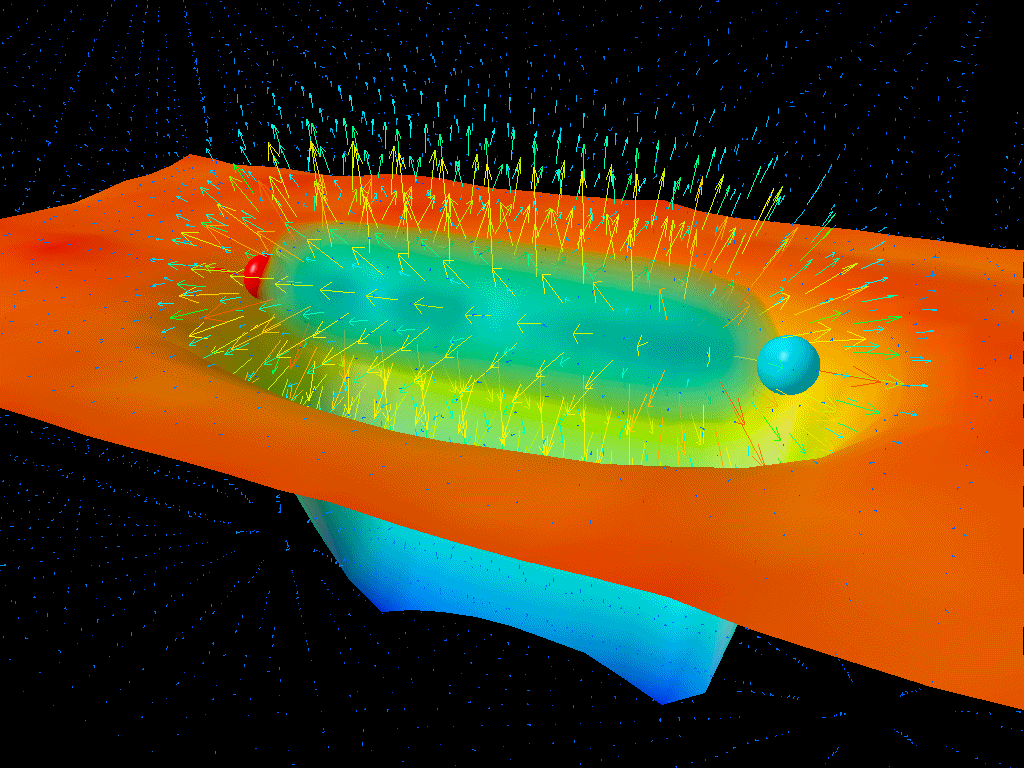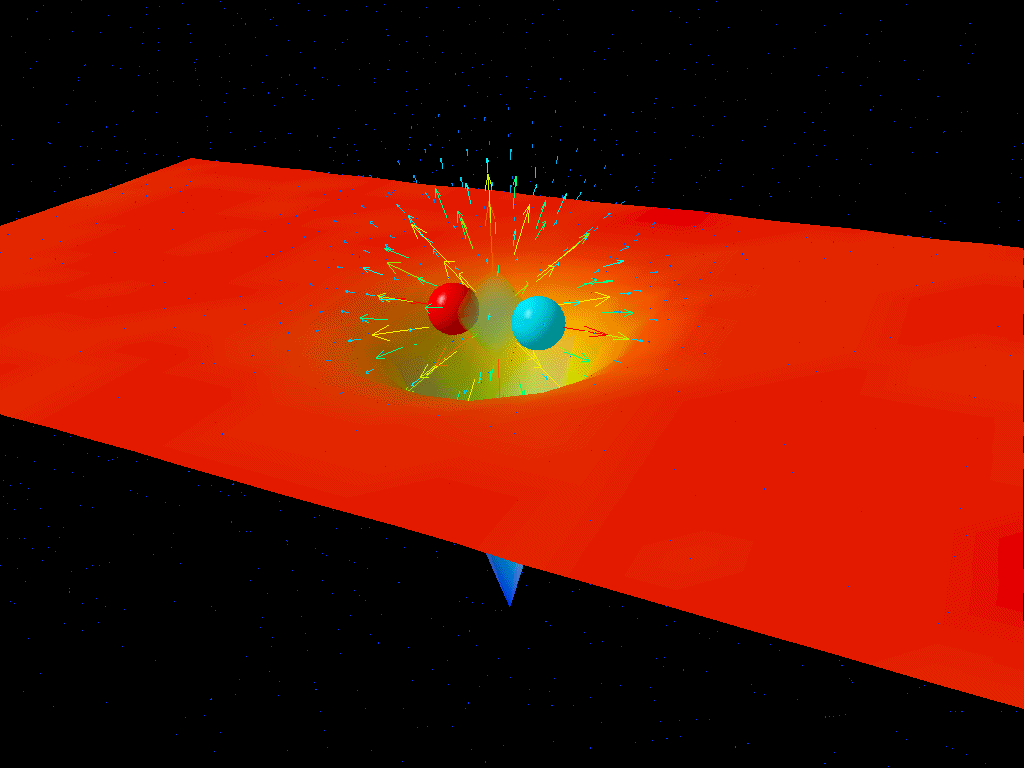
3:59 PM: Lattice QCD is an entirely different approach. Instead of writing out an infinite series that diverges after some time, which we call a perturbative approach, this is a computationally-heavy one that takes a non-perturbative approach. If you could achieve arbitrarily large computational power and arbitrarily small lattice spacing, you’d be able to calculate amplitudes, couplings, and even composite-particle masses to arbitrary accuracy. That’s the power of this approach, and why I’m so excited for this talk!

4:00 PM: Okay, and here we go; let’s see what’s in store now that we’re all here!

4:02 PM: Hey, can you believe it? It’s Heather Clark doing the introduction, marking the first time I’ve seen a woman introduce the lecturer at Perimeter Institute for their public lecture. It may be a tiny barrier to be broken, and it may only be broken in my mind, but I’m still happy to see her in this role!

4:04 PM: And here we go! She is going to be talking about an incredibly major and existential question here: what are the fundamental building blocks of the Universe? We might be able to point to the Standard Model, but that doesn’t do the entire thing justice; we can go to deeper and deeper substructures, and we aren’t sure we’ve even hit the fundamental limit. Plus, we already know there’s more “stuff” out there than what we know: dark matter and dark energy, and perhaps even more particles that may exist at higher and higher energies. We don’t know yet.

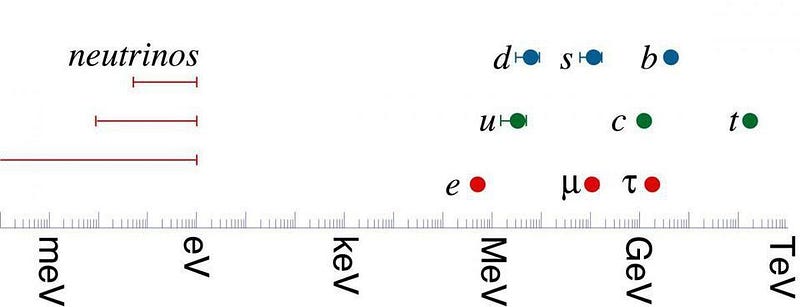
4:08 PM: We do know, however, that the Standard Model particles have the properties they do under the strong, weak, and electromagnetic forces. We know their rest masses, which is what we call inertial mass. We’ve observed that these inertial masses seem to be equivalent to the gravitational mass that particles experience when you place them amidst the fabric of General Relativistic space. But we do not yet understand why, or whether there is an absolute equivalence here.

4:11 PM: If we want to go beyond the Standard Model, and Phiala is putting forth and incredibly important point here, we have to absolutely understand what the Standard Model predicts. And that means understanding how every particle within it goes together, works together, gets created, gets destroyed, decays, etc. We might be looking for tiny corrections to the Standard Model’s predictions, so we have to do incredibly detailed calculations to understand, at incredibly high precision, what the Standard Model actually predicts.

4:12 PM: I am so happy that already, she is into the meat of her talk, explaining the grid-like technique of Lattice QCD and the challenge of using the strong force, gluons, quarks, and the inner workings of baryons to try and understand how these composite particles emerge, remain stable, and how they get their properties. (Such as mass, for example.)

4:14 PM: Here’s an interesting result that’s new and that I did not know: the mass difference between a proton and neutron, which is about 1.3 MeV/c² (or about 0.14% the mass of either one), actually receives a positive contribution from the strong force and a negative contribution from the electroweak force! The positive contribution from the strong force is greater, and that’s why a neutron is heavier than a proton, and can decay into one (plus and electron and an antineutrino), but not the other way around.

4:15 PM: Phiala said the first thing I might disagree with: that the United States will build a new, cutting-edge particle collider between electrons and ions. It’s being planned and I hope it gets built, but I trust absolutely nothing in today’s political climate.

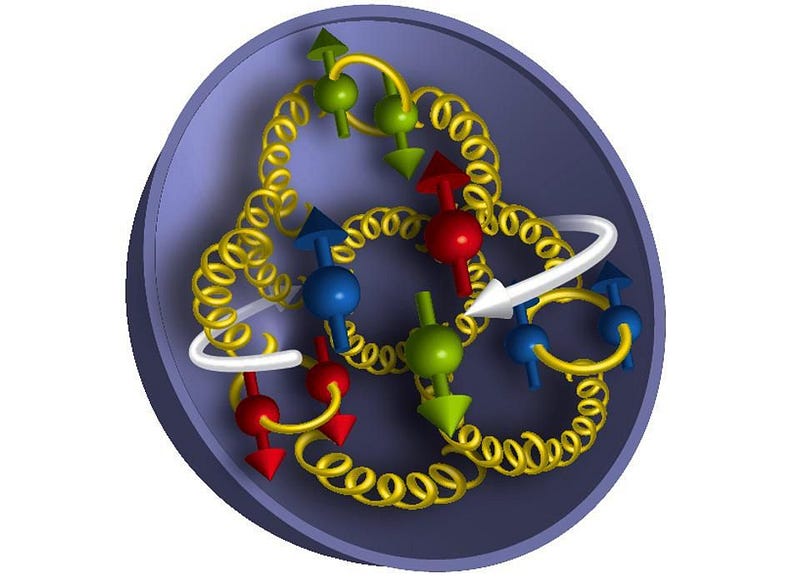
4:17 PM: It’s so important, if we want to understand how protons work, to actually understand their internal structure. We can do this theoretically, and we can probe it experimentally through deep inelastic scattering, by firing individual, point particles at them. This is why an electron-proton or an electron-ion collider is so important: to get the experimental data that can tell us how our theories are doing! I really like how Phiala is emphasizing the experiment-theory connection, rather than exclusively valuing one over the other.

4:20 PM: Here are some of the biggest unsolved problems in theoretical physics:

• Why is there more matter than antimatter?
• What is the nature of the apparent dark matter, required to hold galaxy clusters together?
• Why does the Universe expand at the accelerated rate we observe?
• And why do the particles that we know of have the masses that they do?

Excitingly (for me), Phiala promises that we will be focusing for a large fraction of the remaining talk on the dark matter problem. I am not aware of a connection to this with nuclear physics or QCD, so I’m extremely excited. (Of course, it could just be a supercomputer analogy, rather than a Lattice QCD analogy, but either way I’m game.)

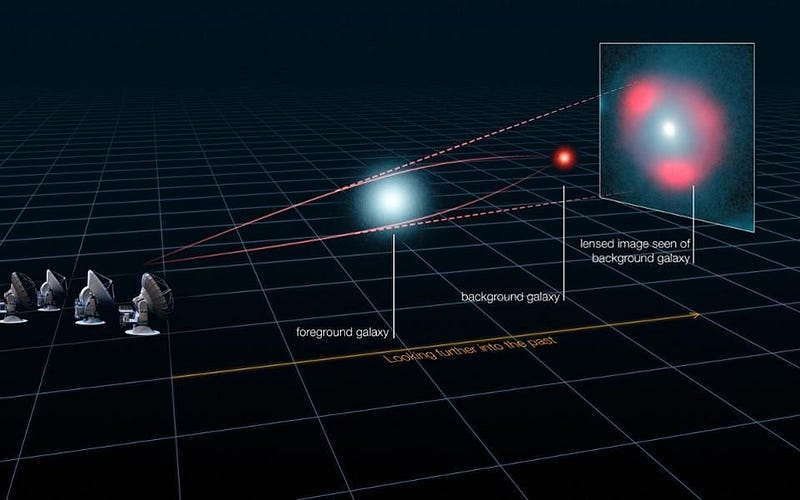
4:23 PM: There’s a whole suite of evidence supporting the existence of dark matter astrophysically, particularly on large scales. This includes gravitational lensing, both strong and weak, the motions of individual galaxies within clusters, the separation of visible mass and inferred mass in colliding large-scale structures, and cosmological details in the cosmic microwave background and the large-scale structure of the Universe.

Happily, she’s putting in a lot of astrophysics background here, including details of colliding galaxy clusters!

4:25 PM: I really like this idea she’s putting forth: that dark matter, of the four fundamental forces, may only interact gravitationally. It doesn’t interact electromagnetically, it doesn’t interact through the strong force, and it may interact with the weak force but if it does, it’s highly constrained. Most of what we can say about dark matter is what it doesn’t do, and what models of dark matter are constrained or ruled out.

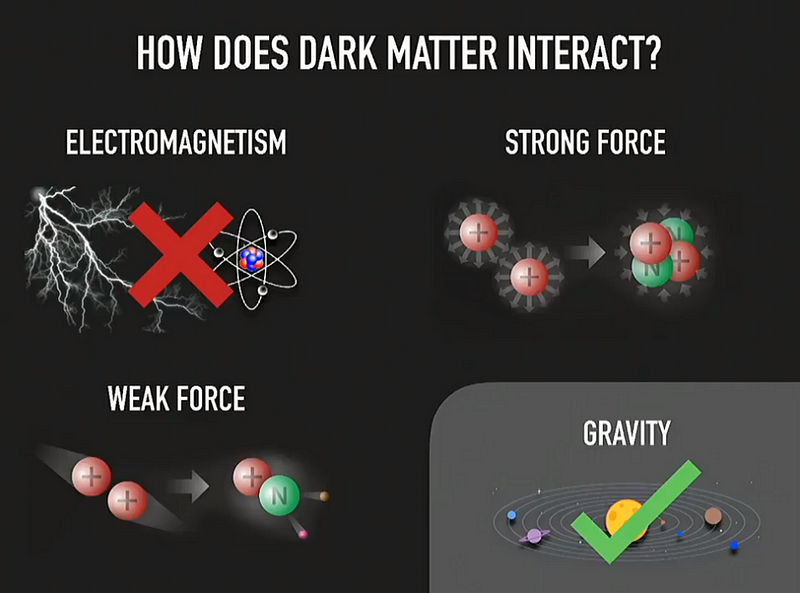
4:28 PM: Can you create dark matter in a lab? Sure: by colliding known particles with one another and seeing them just disappear. Dark matter, since it’s so difficult to detect, must be invisible. Unfortunately, neutrinos also do this, implying that we’d need to understand the neutrino background in particle-particle interactions extremely well, and then find an additional signal above the Standard Model background. This is why it’s so difficult to try and find a dark matter signature at colliders; again, all we have is constraints.

4:31 PM: “If we see dark matter at one of these experiments tomorrow, before we can really interpret what it is, we need to do a lot more work to understand the theory.” This is a huge point: the direct detection experiments we’re performing, where we’re hoping that either a dark matter-normal matter interaction or a dark matter-dark matter interaction in the presence of normal matter occurs, won’t know what to make of it if we actually see a non-zero signal. It will take a tremendous amount of computational work to get there, and that’s something that lattice QCD can help us with, but only if we have an experimental hint to help guide us. Doing blind calculations without additional information is simply too computationally expensive, even today.

4:34 PM: Think about this: if a dark matter particle collides with an atomic nucleus, it’s going to recoil. But many of the experiments, to maximize the chance of an interaction, maximize the particle cross-section, which means they use a heavy nucleus. The XENON experiment is an example, but what happens if a dark matter particle collides with a xenon nucleus, with over 100 nucleons (protons and neutrons) inside? You have a big QCD challenge ahead of you to understand what’s going on, and to reconstruct it.

Not a pretty problem, but it is an important one. Perhaps someday, we’ll be lucky enough to need to solve this problem, because there’s a recoil/detection above the Standard Model’s background.

4:35 PM: There are other, simpler questions, like “what is the size of a proton?” This requires computational advances, particularly because the theoretical predictions and the experimental observations disagree at like the ~4% level, with just 0.5% uncertainties. That’s troubling, right?!

4:38 PM: So what can you do? Phiala showed how computational power is increasing, and yet, even if it continues to increase at an exponential rate for the rest of her life (and she’s under 30!), we won’t be able to perform the calculations required to solve the problems she’s referring to. That means we don’t just need better computers, we need better techniques. We need superior algorithms, and that’s a difficult and challenging task!

Unfortunately, she can only give us the motivation for doing so, not the actual algorithms themselves.

4:39 PM: She’s talking about the potential of quantum computing, and could we either make a tremendous advance, or use a tiny piece of quantum computing to lead to an advance in the problems we’re trying to solve?

Any tech-heads listening to this talk should be incredibly excited at around this point; I feel that she’s really talking about the future of computers here, and not just in the “let’s use a single electron to store a binary bit” way, but in a “let’s calculate the size of a proton” way with a specialized, simpler computer than the generic supercomputers we have today.

4:42 PM: “The standard model has withstood every test we’ve thrown at it… other than the ones I’ve mentioned.” That is absolutely hilarious, and true, and details just how maddening the current situation is. We have the Standard Model which works so, so well in all the areas we know how to investigate. But in the areas we don’t know how to investigate in terms of the Standard Model, there is so, so much that we don’t understand at all.

4:43 PM: And that’s it! Quick talk, but packed full of information. Q&A time now!

4:46 PM: Could dark matter be related to the matter-antimatter symmetry? It’s a deep question. There are four major scenarios for the matter-antimatter asymmetry:

• GUT-scale baryogenesis,
• new-electroweak-physics baryogenesis,
• leptogenesis that produces a baryon asymmetry through sphaleron interactions,
• or scalar-field-based baryogenesis through a mechanism like Affleck-Dine.

If there’s new physics there, it could be related to the physics that generates dark matter. We traditionally look at these as separate problems, but they may be related.

4:48 PM: So frustrating for her, but what an honest answer! The biggest problems she wants to solve is the proton radius problem. She says, with a computer of enough power, she could compute the proton’s radius exactly, and we could know what theory actually predicts, and whether there’s something wrong with experiment. But without a custom computer or a better algorithm or something “new,” she won’t be able to solve many of the other problems she wants to know the answer to.

In terms of, “puzzles that keep you up at night,” those are pretty good ones!

4:50 PM: One of the things I love about this talk is that despite all the things we don’t know, not everything is possible. There are so many ideas that seem like they could solve some of these big, big problems, but almost all of them are already ruled out. The reason is that the level of precision that we know the fundamental laws and rules and properties of physics to are so highly constrained, that it’s virtually impossible to solve these problems without something “new” and novel, that goes beyond our standard, current understanding.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

4:51 PM: And I completely agree with her answer to the last question: build your foundations across a wide variety of disciplines if you want to work on the fundamental questions in theoretical physics. Learn computer programming. Learn a whole suite of science, from biology to chemistry to physics to mathematics. Learn a variety of techniques; these will translate into your toolbox for problem-solving. And engage in projects and work on problems that interest you and, if you can, that not everyone-under-the-Sun is working on.

Your reward will be a unique education and set of tools that could lead you down a road that no one else has traveled before.

Thanks for tuning in, and hope you enjoyed the talk and the live-blog!