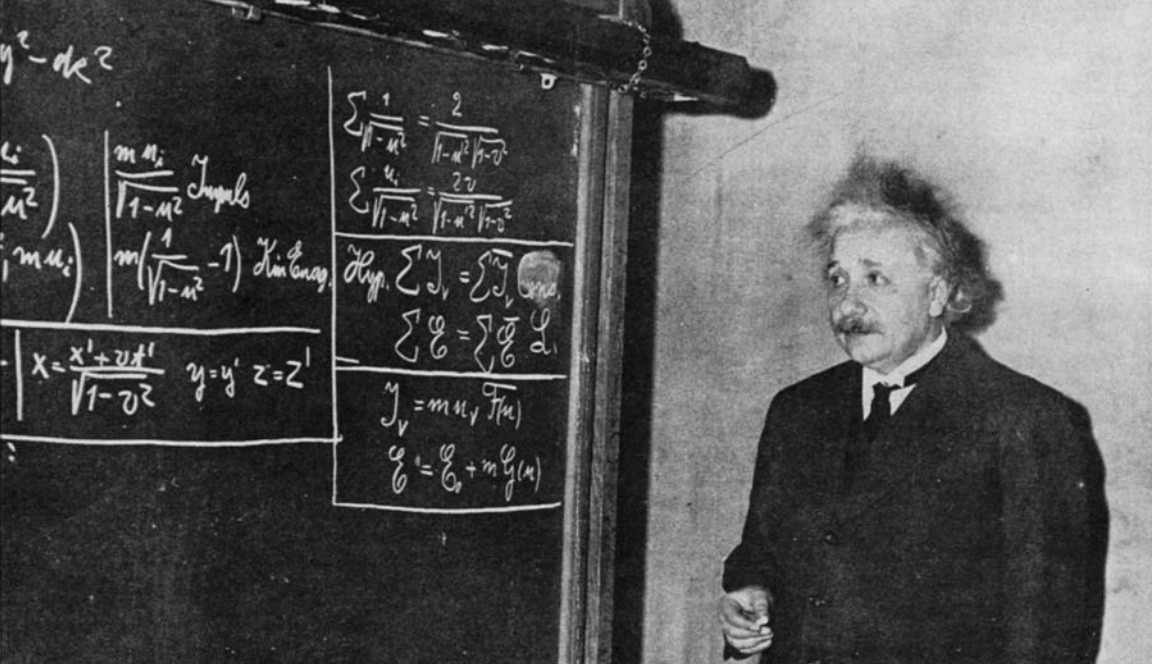Einstein’s top professor didn’t believe in his abilities

- Many, maybe even most of us, had a memorable experience dating back to our school days where someone whose opinion mattered to us thought very little of us, our abilities, and our potential.
- Being underestimated and unvalued in a field can easily destroy a student’s potential interest in joining that field, but can alternatively provide motivation to “prove the doubters wrong” or persist despite obstacles.
- In the case of Einstein, his former professor Hermann Minkowski’s perspective was easy to understand and sympathize with. The key lesson to learn, however, is to maintain a growth mindset when it comes to others.
Just like so many of us, Einstein’s early life was filled with people who believed in him — teachers, family members, and peers — but also with a few notable people who had no faith in his abilities and saw little potential for success within him. Of all the people who had Einstein as a student, by far the most famous and prestigious was mathematician Hermann Minkowski: a daring mathematical genius who himself was a child prodigy, winning the French Academy of Sciences’ Mathematics Prize at the unheard of age of 18, and who earned his doctorate at just age 20. Minkowski was best friends with David Hilbert, perhaps the greatest mathematician in all of the 19th and 20th centuries.
At the Eidgenössische Polytechnikum, which today is the Swiss public research university ETH Zurich, Minkowski had Einstein as a student in his classes. He remembered Einstein as:
- “always skipping lectures,”
- “being a real lazybones… who never bothered about mathematics at all,”
- and as having a “mathematical education [that] was not very solid.”
Less than a decade after teaching Einstein, a disbelieving Minkowski would build the first mathematical “spacetime” relevant to the theory of relativity: the Minkowski space that’s still used by physicists to this day. Here are the life lessons we should all learn from Minkowski’s experiences with Einstein.

Performance is how Minkowski evaluated Einstein
From the perspective of a teacher and professor like Minkowski, the best way to evaluate a student is to look at the quality of their work with respect to the problems you’ve given them to solve. In a field like mathematics, this normally involves three key aspects.
- Can the student comprehend the assigned problems in such a way that they understand what is being asked and what foundational knowledge should be leveraged in order to approach it in a useful fashion?
- Can the student correctly set up the mathematics in a way that could successfully solve the problem, if they work out all of the relevant and necessary steps correctly?
- And then, can the student carry out each of the steps, successfully and in their proper order, in order to arrive at the solution to the problem under consideration?
In addition to those standard assessments, professors can also fold in aspects such as student participation in class, the quality and depth of questions that they ask, and their curiosity about a variety of topics that are expressed through direct interactions with those students.
From all of these perspectives, individually as well as cumulatively, Minkowski was well within his rights to deem Einstein as a “low performer.”

After all, Einstein often skipped class, which Minkowski correctly noted was a terrible strategy for someone who was looking to revolutionize how we all conceived of the Universe behaving at a fundamental level. In his own (translated) words, Minkowski stated:
“Oh, that Einstein, always cutting/skipping lectures… I really would not believe him capable of it.”
As far as his homework and other assessments were concerned, Minkowski really was in disbelief that his former student had the potential within him to even conceive of the idea that would spur him to develop the special theory of relativity. On that front, Minkowski was quoted as saying:
“It came as a tremendous surprise, for in his student days Einstein had been a lazy dog… He never bothered about mathematics at all.”
And as far as his fitness as a mathematician was concerned, Minkowski had perhaps the most damning assessment of Einstein of all, noting:
“The mathematical education of the young physicist [Albert Einstein] was not very solid, which I am in a good position to evaluate since he obtained it from me in Zurich some time ago.”
And yet, every one of Minkowski’s critical assessments of Einstein would prove to be foolish in hindsight.

Performance is not the same as potential
It’s easy to look at how someone performs — especially if that person is young, inexperienced, or poorly prepared for the challenges they’re presently facing — and judge their potential based on where they are at that present moment. If you do that, you’re almost certainly going to overlook the following categories of students:
- Students who have the capacity to perform at an extremely high level, but who haven’t learned or demonstrated the proper study habits just yet.
- Students who have the intellectual acumen to ask deep questions and have profound physical insights, but whose problem-solving skills or foundational skills need work to apply them properly to the problems in question.
- Students who have the potential to be extremely successful in your field, but who haven’t figured out how to apply themselves in all of the important ways, simultaneously, that will lead to success.
In other words, it’s easy to look at a student’s sub-par performance and conclude that this is a student without the potential to succeed in the future, but that masks the truth that many of us so often fail to recognize: performance and potential are not the same things as one another.

If you find yourself in Minkowski’s position, make sure you recognize the trap that he fell into. Oftentimes, the student that you dismiss today will turn around and be a tremendous success tomorrow, and you’ll find that you could have been a part of their success if only you had given them more of a chance. There are plenty of students who want to go on to pursue more advanced studies in fields where they’ve demonstrated less-than-exceptional performance up to the present moment, and who will indeed go on to achieve successful careers in those fields.
- There are students who have never been compelled to apply themselves with a large, sustained effort, but who have it within them to make that effort and to succeed once they do make it.
- There are students who believe their present limitations will hold them back, rather than seeing a path toward developing those necessary skills and then using those developed skills to use their creative talents in new and innovative ways.
- There are students who only require a sufficiently interesting (to them) problem to motivate them to work up to their full potential; students who are only confronted with problems that fail to pique their interest will often fail to rise to the expectations of others.
- And there are students out there who you may have dismissed in their past, based upon their performance at the time, who have since grown and improved and are succeeding.
Oftentimes, what we all need is for someone who knew us from our past, back before we learned how to be successful, to look at our growth and subsequent achievements with fresh eyes.

Einstein’s path
It would have been very easy, in the late 1890s and early 1900s, to look at Einstein as I’m sure Minkowski and many of his other professors did: as a failed mathematics/physics student who “washed out” of the field before even comprehending the vast intellectual sea that lay before him. While Minkowski himself was working on quadratic forms and geometric properties of problems with arbitrary numbers of variables and dimensions, making tremendous advances linking geometrical methods to problems in number theory and having numerous aspects of mathematics named after him, Einstein had left academics entirely and was working at the Swiss patent office as a clerk.
But, unbeknownst to Minkowski, Einstein was anything but “done” with physics, mathematics, and academics in general. After graduating from Zurich in 1900, Einstein continued to concurrently study physics and mathematics (taking what we would call “continuing education” classes), while remaining friends and studying new problems and recent papers with many of his old classmates, including:
- Marcel Grossman, whose father got Einstein the job at the patent office so that Einstein could finance his education,
- Conrad Habight, a mathematician who would form the informal “Olympia Academy” with Einstein to regularly study physics and philosophy,
- and Maurice Solovine, a philosopher who would learn physics from Einstein and mathematics from Habicht, a co-founder of the Olympia Academy who would often perform French-German translations for Einstein.
Through this sort of independent study, Einstein developed the necessary skills to turn his ideas into full-fledged, robust physical and mathematical theories.

Perhaps all of that “extracurricular” study that Einstein did would really pay off. Back in 1885, the journal Nature featured a pseudonymous article, published under the name “S,” that conceived of a four-dimensional version of space, with time standing in as the fourth dimension. In 1887, a student at Imperial College, London named E.A. Hamilton Gordon contributed an article with similar ideas called “Fourth Dimension.” In 1888, then-student H.G. Wells wrote a short story called “The Chronic Argonauts”, which he would later expand into his famous 1895 novella: The Time Machine.
By thinking about the properties of objects as they moved close to the speed of light — including the properties of length contraction and time dilation, which had been worked out in the late 1800s by Hendrik Lorentz and George FitzGerald — Einstein realized that space and time were linked together: through the motion of objects that traveled through them. In particular, Einstein recognized that every unique observer, at their own unique location with their own unique direction-and-magnitude of motion, would experience the idea of distance and time differently.
Einstein was the first to correctly put all of these puzzle pieces together, including the constancy of the speed of light for everyone, in formulating his special theory of relativity in 1905.
Einstein takes off… and Minkowski follows!
If Einstein had only contributed special relativity to the world, his fame would have been assured. But that special relativity publication was one of five papers he published that year, all of which were remarkable.
His first paper, published in 1905, was on the topic of the photoelectric effect. It would be for this work, which would form part of the particle-aspect foundation for quantum mechanics, that Einstein would be awarded 1921’s Nobel Prize in physics.
His second publication was no paper, but rather was his doctoral dissertation, completed with experimental physicist Alfred Kleiner at the University of Zurich on the topic of the dimensions of molecules. In particular, Einstein was leveraging a new method for calculating Avogadro’s number: the number of atoms in a mole. Although his initial estimates were off by a factor of three, subsequent refinements led to a value that was off by only 9%.
His third publication was on the topic of Brownian motion, or the seemingly random motion of small particles suspended in a stationary liquid. (You can perform a similar experiment at home by dropping a small drop of food coloring into hot and cold glasses of still water.) It supported the kinetic theory of gases and the physical reality of atoms.
Special relativity was Einstein’s fourth publication of 1905.
And his fifth and final paper, on the topic of whether the inertia (i.e., rest mass) of a body depended on its energy content, would give rise to his most famous equation of all: E = mc².

Clearly, Minkowski had missed the mark in his assessment. Whereas he had only seen a lazy, oft-absent student who wasn’t putting in the effort to succeed at the mathematics he was attempting to teach, he had missed out on the deeply creative mind that was thinking hard about important problems that were plaguing some of the best minds of his time. He missed the strong physical intuition that Einstein possessed, and Einstein’s key ability to synthesize together bits of information from cross-disciplinary areas that would allow him to make a number of important breakthroughs. Minkowski, perhaps because of his obsession with mathematical rigor and a narrow focus on a particular set of details, was blind to Einstein’s brilliance, even as his teacher.
But this in no way would deter Minkowski from immediately setting his own formidable skills and talents to work on the very problems that Einstein had now put front-and-center in the minds of so many. Minkowski published a paper in 1907/8 elaborating on special relativity, where he reframed Maxwell’s electromagnetic equations in a four-dimensional, relativistically invariant formulation. This led to what I would argue is Minkowski’s greatest contribution to physics: his notion of a unified, four-dimensional fabric known as spacetime.
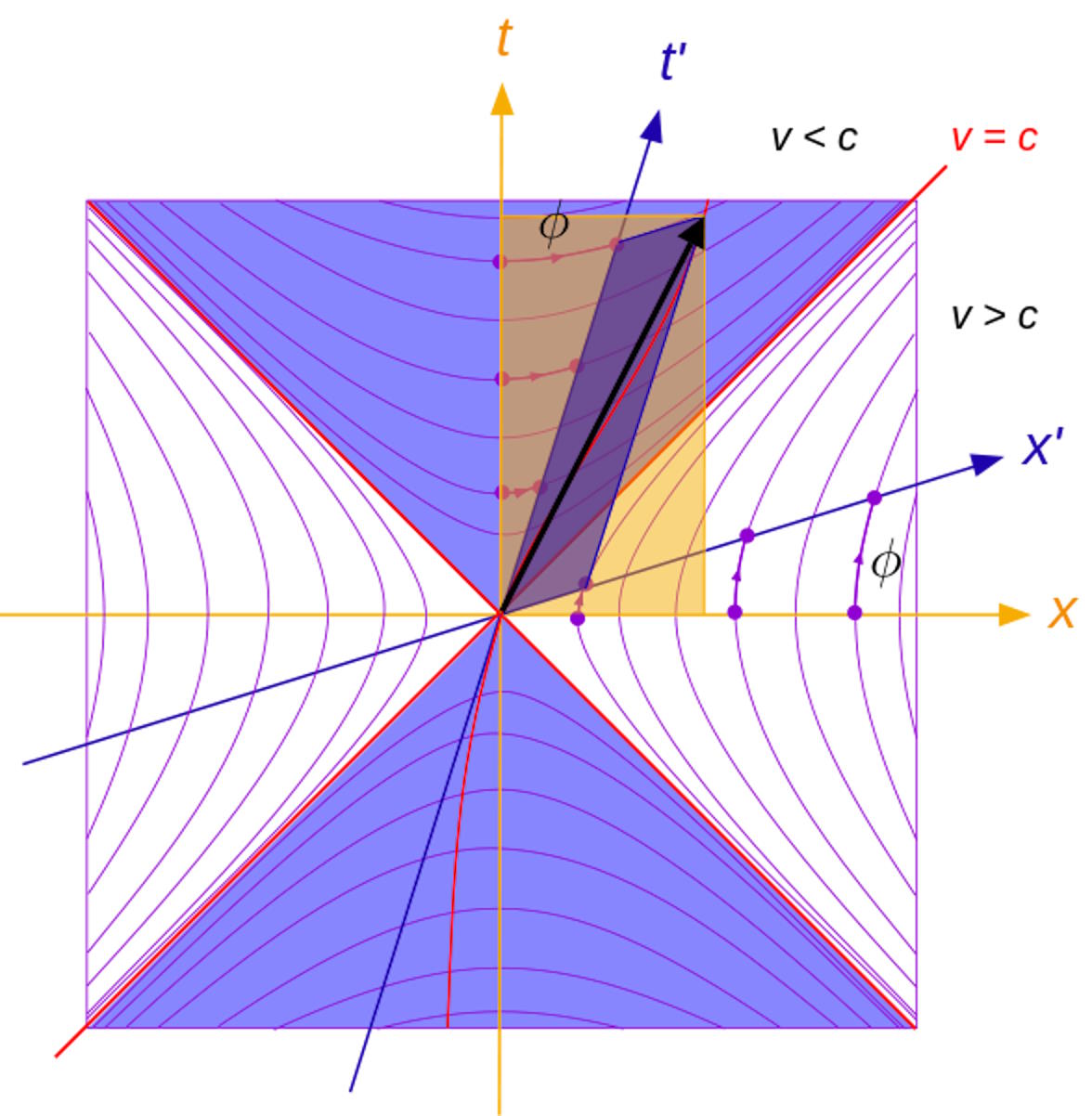
Minkowski became the first to develop the notion of what’s truly invariant in relativity: not space, not time, but rather the difference between the square of them: known as the Einstein (or spacetime) interval. He developed a new tool for representing space, time, and the motion of an object through it: the Minkowski diagram. They allow us to generalize Newton’s laws of motion to relativistic regimes, and it would be the generalization of Minkowski’s spacetime to curved space that would enable Einstein to develop general relativity: our new and current best theory of gravitation.
Aware of how space and time could not sensibly exist on their own any longer, Minkowski gave a now-famed lecture in 1908 where he declared:
“The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”
Although Minkowski would die suddenly of appendicitis in early 1909, his lasting legacy and brilliance come with a cautionary tale: don’t dismiss the potential of your students based solely on their performance. With sufficient cultivation and hard work, they may yet turn out to far surpass anything you can fathom for them.