Ask Ethan: How is energy conserved when neutrinos oscillate?

One of the most surprising discoveries in the 20th century was the realization that neutrinos don’t necessarily remain the same species of particle as they travel through the Universe but rather can change from one type of neutrino (electron, muon, or tau) into another. This taught us that the original formulation of the Standard Model, which asserted that neutrinos would be completely massless, was fundamentally incomplete, and that neutrinos would instead be required to have mass. As of 2023, it’s still the only known way that particle physics has given us any indication that something else is out there beyond the Standard Model.

But it raises an interesting puzzle. After all, if there are three species of massive neutrino (and antineutrino) out there in the Universe, the observations teach us that the neutrinos themselves all have different rest masses from one another. Does this mean that when they oscillate from one species to another, since E =mc², that energy is no longer conserved? That’s what Alan Finkel wants to know, asking:

“Given that neutrinos are known to oscillate between flavors, and each flavor is a different mass-energy, how is the energy conserved?”

I’ll spoil you first: energy really is conserved. But in order to understand how, you first need to understand quite a few counterintuitive things about neutrinos themselves. Let’s start at the beginning.

The neutrino is an intriguing and interesting particle. This infographic lays out some of the neutrino’s basic stats alongside fun facts.

Neutrinos began as a purely theoretical concoction to solve a problem: the problem of energy conservation in radioactive decays. In the early days of nuclear and particle physics, we knew that some atomic nuclei — that is, bound combinations of protons and neutrons — were unstable, and would emit one or more particles. The three main types that we knew of were:

1. alpha (α) decay: where a nucleus emits “an α-particle” (or a helium-4 nucleus) with 2 protons and 2 neutrons, where the daughter nucleus and the α-particle, combined, conserve both the energy and momentum of the original nucleus.
2. beta (β) decay: where a nucleus emits “a β-particle” (or an electron), transforming one of the original nucleus’s neutrons into a proton, where the electron and the daughter nucleus’s energy and momentum were almost, but not quite, conserved.
3. gamma (γ) decay: where a nucleus in an excited state (i.e., with a heavier rest mass than a typical, ground-state nucleus) emits a high-energy photon (also known as a γ-particle), and rearranges itself into a lower-energy state while keeping the same number of protons and neutrons. The new nucleus plus the emitted photon, when compared to the original nucleus, also conserve both energy and momentum.

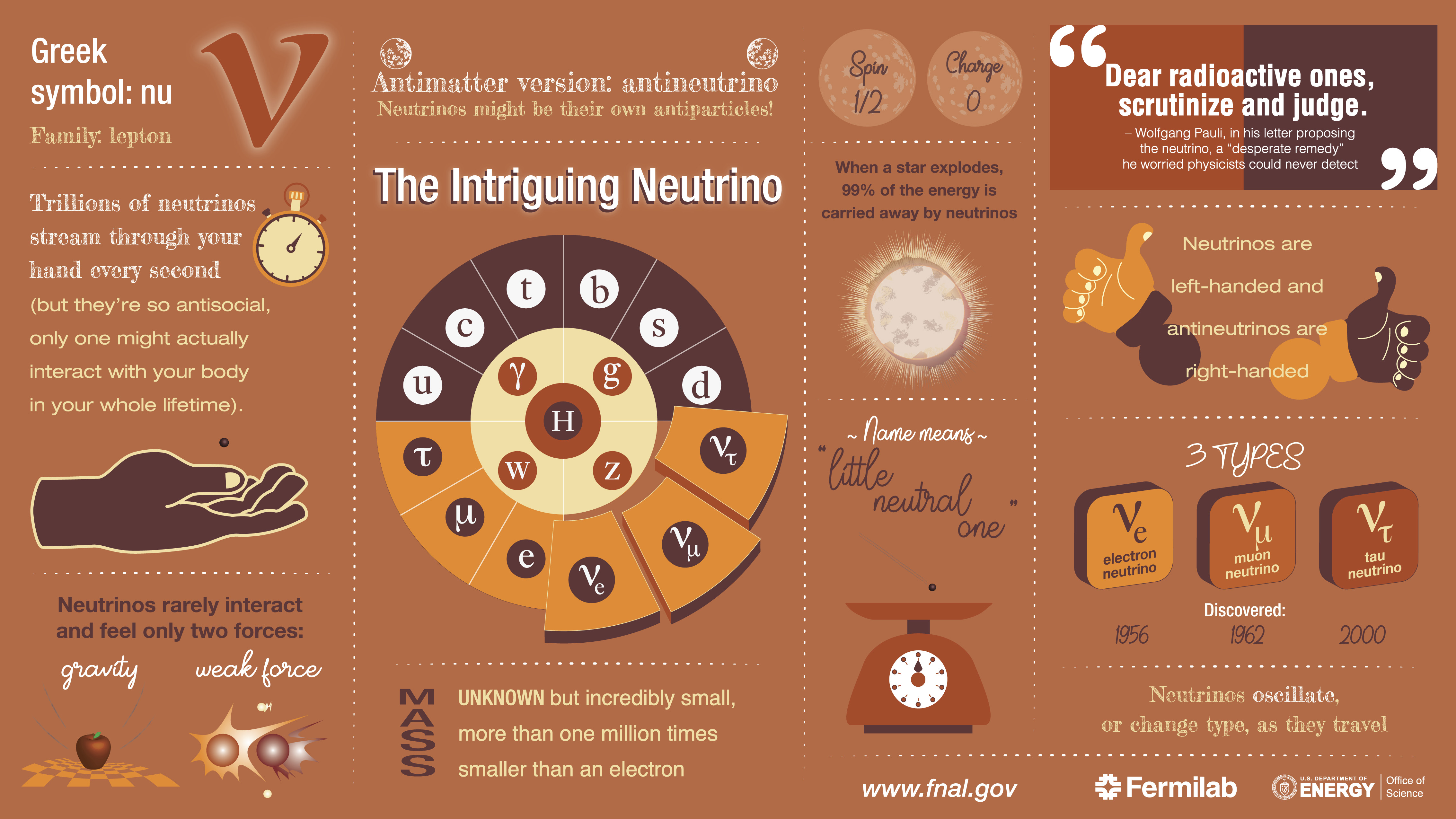
The problem was with β-decay, and that’s what led Wolfgang Pauli, in 1930, to hypothesize the existence of a new particle: the neutrino.

Schematic illustration of nuclear beta decay in a massive atomic nucleus. Only if the (missing) neutrino energy and momentum is included can these quantities be conserved. The transition from a neutron to a proton (and an electron and an antielectron neutrino) is energetically favorable, with the additional mass getting converted into the kinetic energy of the decay products.

In Pauli’s formulation, there would be an extra particle that was emitted during β-decay — a particle that was nearly invisible and that had never been detected — that carried away that “missing” energy and momentum, and which allowed for everything to be conserved, after all. Because that particle needed to have no electric charge and had to be extremely low in mass, as the “missing energy” from many observed β-decay events was barely perceptible, Pauli named it a neutrino: Italian for “little neutral one.”

Of course, Pauli was extremely disappointed with his own proposed solution to the β-decay problem, stating, “I have done a terrible thing, I have postulated a particle that cannot be detected.”

Although it took a further 26 years for the first neutrino (technically, an antineutrino produced by a nuclear reactor) to be detected, it was quickly realized that not only were neutrinos real, but they played a tremendously important role in nuclear physics, and in particular in the fusion reactions that occur inside stars. In the 1960s, scientists began building larger and more sensitive neutrino detectors, and finally began detecting neutrinos generated in the nuclear reactions inside our own Sun. And immediately, a terrible, new problem arrived on our doorstep.

It isn’t just photons and charged particles that carry energy away from the Sun, but also solar neutrinos, which are produced in the Sun’s core and hardly interact at all with other particles. A total of approximately ~1% of the Sun’s energy is emitted in the form of these solar neutrinos.

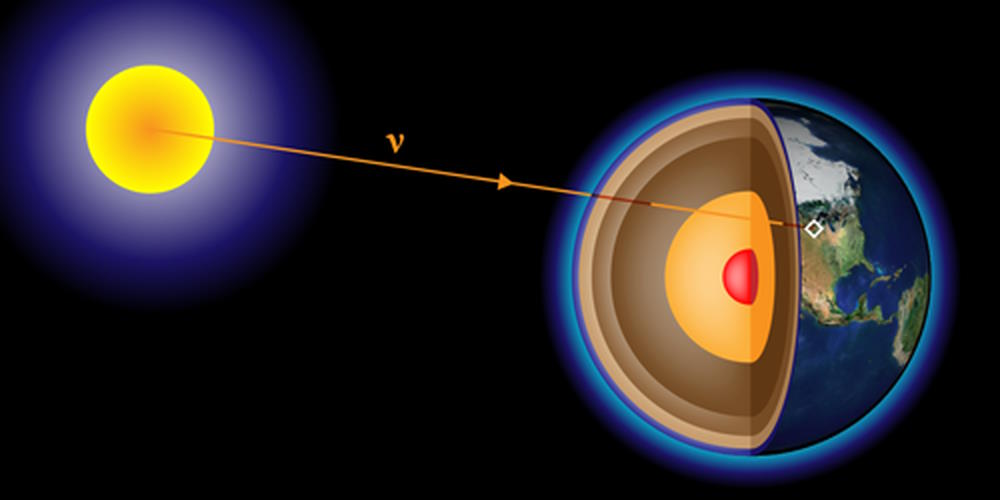
You see, we know how stars work. By the 1960s, we knew more than just the basics of how fusion in stars worked: we knew how to calculate how many neutrinos should be produced and how much energy they ought to carry away. And because we had begun to detect neutrinos directly, we also believed we knew what their cross-section (which determines their interaction rate) should be inside a detector, and hence we had a theoretical prediction for the rate and energy distribution of neutrinos that we expected to see.

When the data began coming in, things started to look really good. Right away, neutrino signals started appearing in the detector, with the right energies, momenta, and direction to be consistent with being generated by the Sun: solar neutrinos. The experiment was working! As the scientists collected more and more data, they began to see the shape of the energy spectrum, and once again, it matched up with the theoretical predictions very well.

It led a great many scientists to believe that we actually knew what we were talking about when it came to neutrinos, despite their elusive nature. But others strongly disagreed, because there was one big puzzle that arose from the data: despite everything we expected, only about ⅓ of the expected number of neutrinos that we anticipated seeing were actually appearing in the detector.

Experiments such as Super-Kamiokande, which contain enormous tanks of (proton-rich) water surrounded by arrays of detectors, are the most sensitive tools humanity has to detect neutrinos from the Sun. Compared to the number of electron neutrinos we naively expected to appear in the detector, the measured signal is only about one-third of the predicted value.

This puzzle soon became known as the solar neutrino problem. Many physicists in the community were quick to dismiss the importance of the problem, as they believed that either:

• the experimental physicists working on the detection side didn’t know what they were doing and had built a less-efficient detector than they had expected,
• or that the theorists working on calculating their models of the Sun and the neutrino flux it emitted over time didn’t know what they were doing, and their calculations were simply predicting absurdities that didn’t line up with what we saw.

Physics is hard, after all, and it wouldn’t have been too surprising if one of these avenues had turned out to be correct. But the solar neutrino problem was a stubborn one; as more and more neutrino detectors were constructed and we began detecting them in multiple ways, we began ruling out the possibility that experimentalists were in error. As our understanding of stars, neutrinos, and nuclear & particle physics improved, we began to exclude a variety of possible sources of error that theorists could’ve been making. By the 1980s and 1990s, it became abundantly clear that the original claims of both experimentalists and theorists working on the solar neutrino problem had been correct all along, and something really was amiss.

While cosmic ray showers are common from high-energy particles, it’s mostly photons, muons, neutrinos, and electrons that make it down to Earth’s surface. Almost all of the neutrinos produced via cosmic ray showers are muon neutrinos, but that doesn’t necessarily mean all of the detected neutrinos will be muon neutrinos.

A huge clue came along when we became sensitive to detecting a second source of naturally-produced neutrinos: neutrinos generated in Earth’s atmosphere. You see, the Universe is filled with cosmic rays: high-energy particles, mostly protons, of astrophysical origin that come from all throughout the Universe. When those particles strike the top of the atmosphere, they produce particle showers: largely pions, which come in three varieties: π⁺, π^–, and π⁰. The neutral pions (π⁰) that are produced decay into photons, but the charged pions (π⁺ and π^–) decay, mostly into muons (and antimuons) and a different species of neutrino: muon neutrinos (and antineutrinos).

Once again, theorists went through the trouble of calculating the expected flux of neutrinos, and sought to measure their signal strength in the neutrino detector. For the solar neutrinos, they were seeing an event rate that was about ⅓ of what was predicted, but this time, for the atmospheric neutrinos, they were seeing an event rate that was still low, but less low: about ⅔ of what was predicted.

However, this didn’t create a new, atmospheric neutrino problem, but rather pointed the way toward the answer: neutrinos weren’t massless like we had originally anticipated, but rather behaved like the quarks did. They had mass, and therefore they were capable of mixing together, and oscillating from one species into another.

Neutrino detectors, like the one used in the BOREXINO collaboration here, generally have an enormous tank that serves as the target for the experiment, where a neutrino interaction will produce fast-moving charged particles that can then be detected by the surrounding photomultiplier tubes at the ends. These experiments are all sensitive to proton decays as well, and the lack of observed proton decay in BOREXINO, SNOLAB, Kamiokande (and successors) and others have placed very tight constraints on proton decay, as well as very long lifetimes for the proton.

We had known about quark mixing for some time already, and the basic concept is this: there are two ways to look at quarks, in terms of mass and in terms of flavor. When there’s an interaction between two particles and a quark is part of that interaction, some properties of that quark are determined explicitly and do not change when they propagate through space, such as mass. However, if your detectors are sensitive to a different property of those quarks, such as flavor, you’re not going to see a 1-to-1 match between what we call “mass eigenstates” and “flavor eigenstates,” but rather — like so many things in quantum physics — there’s only a probability distribution of what type of flavor you’re going to observe.

If we apply this same reasoning to both solar and atmospheric neutrinos, we can come up with a picture in our heads where, whenever a neutrino is generated, it comes along with a definitive set of properties: it’s a specific flavor of neutrino with a specific rest mass that’s 100% determined. However, when it propagates, it propagates with a fixed mass, but its “flavor” is not. As such, when it interacts with another particle later on (for example, inside your detector), you can only compute a probability distribution for what type of flavor — electron, muon or tau neutrino — you’re actually going to observe.

Vacuum oscillation probabilities for electron (black), muon (blue), and tau (red) neutrinos for a chosen set of mixing parameters, beginning from an initially produced electron neutrino. An accurate measurement of the mixing probabilities over different length baselines can help us understand the physics behind neutrino oscillations and could reveal the existence of any other types of particles that couple to the three known species of neutrino. For neutrinos to oscillate, they must have non-zero mass. If additional particles (such as dark matter particles) carry energy away, the overall neutrino flux will show a deficit.

In the case of solar neutrinos, the interactions inside the Sun initially produce predominantly electron neutrinos and antineutrinos, which then propagate with a fixed, unchanging mass. In the case of atmospheric neutrinos, the interactions between particles (arising from charged pion decays) initially produce predominantly muon neutrinos and antineutrinos, which again propagate with a specific and unchanging mass along their journey subsequent to their generation.

As they propagate through the Universe, however, whether they’re propagating through the vacuum of space or through matter, time is passing for these massive particles. Just like anything quantum mechanical with multiple possible outcomes, the probability of measuring any particular flavor is time-dependent, which means that during the time in-between measurements and/or interactions, the flavor of these neutrinos is not determined: it can be described as a superposition of all three (electron, muon, tau) possibilities.

But the one thing that never changes during the time in between the two interactions — where it’s generated and where it’s detected — is the mass of the neutrino, which remains constant during propagation. Only when it appears in your detector does it take on one of the “flavor” values, and these are less restricted than you might think.

Neutrinos come in a wide variety of energies and have been observed (and calculated) to have a wide variety of cross-sections. Neutrinos have been detected from an enormous number of sources, but never left over from the Big Bang, as their cross-section is far too low to be accessible to experiment. Even so, neutrino-particle interactions should have enough energy, even today, to enable all possible flavor oscillations.

For example, for solar and atmospheric neutrinos, the energy of the neutrinos that appear in our detectors are always in the ~mega-electron-volt (MeV) range or above. By comparison, the rest masses of the neutrinos species themselves are well below a single electron-volt (eV) apiece. Any interaction that occurs between neutrinos (or antineutrinos) and matter (or antimatter) — at least, the interactions that we know how to detect — doesn’t have any mass restriction on what types of oscillations are and are not admissible. With the energies that practically occur, all possibilities are available.

The three flavors of neutrino that we can observe, electron, muon, and tau, do all have different masses, even if we aren’t sure of exactly what those masses are or which flavor is heaviest and which is lightest. But we can imagine a scenario where the lightest, lowest-mass neutrino is slow-moving, however, such as the neutrinos left over from the hot Big Bang. What happens when that neutrino — propagating with its fixed mass — has a very low probability of interacting with some type of matter. However, all the other types of matter that exist are so much more massive than neutrinos that unless they’re practically at rest with respect to one another (which, by the way, would make their probability of interacting negligibly small), there will be enough energy available from the collision to enable oscillation into either of the other two species.

Neutrinos and antineutrinos are copious within this Universe, but we can only detect which flavor (electron, muon, or tau) the neutrino is when it interacts with another particle. During the in-between times, when it’s traveling, it’s in an indeterminate state.

What’s very important to recognize is that energy conservation must always be obeyed, and if you did hypothetically have a low-mass neutrino interact at low-energies with a massive particle, you would have a set of constraints as far as “which type of neutrino” can be revealed from that interaction. If we assume that the tau neutrino is the heaviest and the electron neutrino is lightest, there may be as much as a ~0.03 eV difference (or so) between them in terms of rest mass energy. Unless at least that much kinetic energy is available from the interaction to enable the neutrino to change flavor from an electron neutrino to a tau neutrino, that possibility will be forbidden.

Still, there’s much we don’t yet know about neutrinos, including what the masses of the electron, muon, and tau neutrinos actually are. Measuring solar and atmospheric neutrinos have taught us what the differences between the propagating mass values (technically, the square of those values) are, but we haven’t yet learned what the absolute masses of each of the three types of neutrino actually are, nor do we know which ones are heaviest and which are lightest. Until we learn more, this is the limit of what we know about neutrinos. Rest assured, despite how complicated they may appear, every interaction they ever undergo still obeys the conservation of energy!

Send in your Ask Ethan questions to startswithabang at gmail dot com!