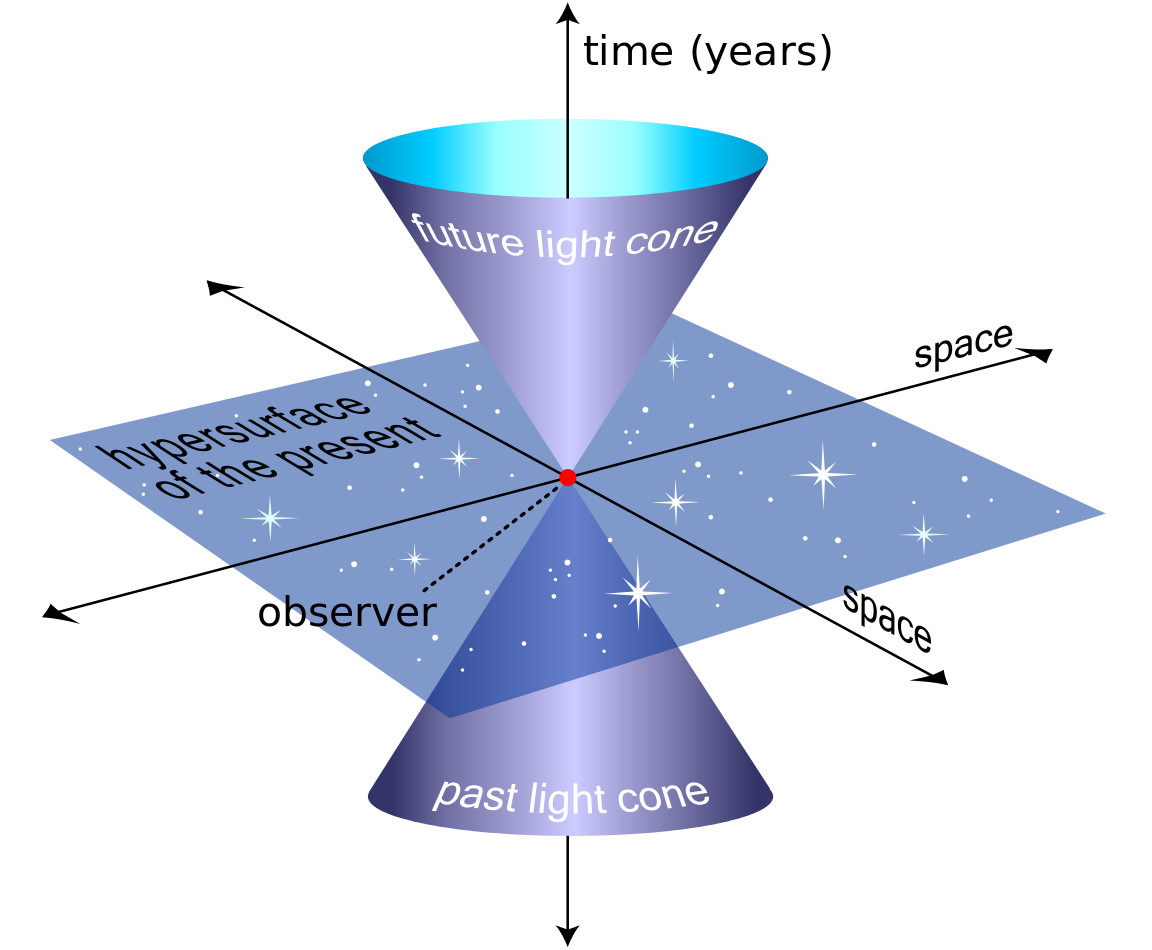
The entropy of a closed system doesn’t always increase

Imagine you’ve got a glass high up on a counter, and it falls down to the floor. Physics tells you what’s going to happen: your glass is going to hit the floor with a specific velocity and with a certain calculable amount of kinetic energy. That impact can easily result in the glass shattering: a spontaneous process that results from the conversion of one form of energy into others. However, the reverse process — of shattered glass shards spontaneously reassembling and leaping the fully assembled glass back onto the counter — never spontaneously occurs. This can be simply explained by the laws of thermodynamics, and in particular by the second law.

A great many of us, particularly in the United States, learn about the second law in terms of entropy: a physical property of all thermodynamic systems. The second law can be expressed in terms of:

• the maximum efficiency of an engine,
• the amount of useful work that can be extracted from a system,
• the spontaneous flow of heat from hot sources to cold ones (and never the reverse process),
• or by the number of possible identical arrangements of the quantum state of your system,

all equivalently and correctly. However, one of the most common ways it’s traditionally been taught is to say, “the entropy of a closed system never decreases,” and this is not true. The entropy of an isolated system never decreases, but isolated is different from closed, and open is still a third, even more different condition. Here’s what everyone should know about entropy, the laws of thermodynamics, and the different types of systems that exist.

If the 2nd law of thermodynamics could truly be violated, then perpetual motion machines would be a physically real possibility. In reality, the 2nd law must always be obeyed, so we must be careful to avoid contradictions in setting up our expectations for a physical system.

Isolating a system

Whenever you consider any physical system, you can always think about various parts of it. There are the components within the system that interact in a self-contained way — like gas molecules flying around inside a sealed box — and then there are components that are external to the system itself, but which can still interact with the system in some fundamental way: generally called “the environment” or something akin to it.

If you consider the total system, one that includes the physical system of interest as well as the surrounding, external environment, this is the ideal case for applying the second law of thermodynamics. When you consider the total system, you’re considering:

• all of the energy that flows between different parts of it, with no energy entering or leaving it,
• all of the particles that interact within the system, with no particles entering or leaving it,
• the entirety of the volume of the system, which doesn’t increase or decrease relative to some external environment or boundary,
• and all of the work done by one part of it on another, with no external sources or sinks of work.

When absolutely everything is accounted for, and nothing is lost or missing, you’re dealing with the total system in its entirety.

In a traditional Schrodinger’s cat experiment, you do not know whether the outcome of a quantum decay has occurred, leading to the cat’s demise or not. Inside the box, the cat will be either alive or dead, depending on whether a radioactive particle decayed or not. Although it’s rarely discussed, the validity of a Schrodinger’s cat experiment depends on the system being isolated from its environment; if the isolation isn’t perfect, the quantum nature of the superposition-of-states will be disrupted.

This is a tall order, of course: to account for every single subatomic particle and every quantum of energy, and to not allow anything from outside this system to affect it in any way, nor to allow anything from inside this system to affect the external environment in any way. (To some who work in the field, they note that “the Universe” is the only true total system, and even that is questionable because the Universe itself is expanding.)

Although it’s quite an idealized case, we can consider every aspect of something within a physical system, and treat it as though nothing from outside that system — no heat, no work, no energy, no particles, etc. — acts on that system externally, and that additionally nothing from inside that system affects or acts on its external environment.

In that ideal situation, you can consider your system to be isolated.

Of the three systems shown here, only the rightmost system can be considered isolated. No energy can enter or leave it, and no matter enters or leaves it, either. On the left, an open system is shown, where matter and energy can both be exchanged with the environment, and at center, a closed system which allows energy (but not matter) exchange is illustrated.

If your isolated system is in thermal equilibrium, which is to say that there’s no

• heat exchange or transfer,
• no moving boundaries to the system (an example of work),
• no input or output of particles,
• no chemical transitions,
• no pumping or other applied forces,
• and that there is no “lower energy state” for any aspect of the system to transition into,

then the total entropy of your system will remain constant, and at its maximum value. Otherwise, if there are parts of the system that

• can transfer or exchange heat,
• can transfer or exchange particles,
• can expand or contract,
• can undergo chemical transitions,
• can pump on another part of the system or exert internal forces,
• and/or can experience transitions to lower-energy states,

then your system’s total entropy will increase with time.

This is always true, and is the heart of the second law of thermodynamics: the entropy of an isolated system will always tend toward a maximum value, and only after reaching its true equilibrium state, where none of the exchanges mentioned above (or any other such changes not specifically enumerated here, such as nuclear transitions) can occur, will its entropy cease to increase: it will remain constant thereafter instead.

The Earth’ is not an isolated thermodynamic system, as it not only receives energy from the Sun and radiates energy back into space, but (at a small level) is impacted by asteroids, comets, the solar wind, and cosmic particles, and also sheds atmospheric particles into space over time.

The opposite of isolated

Of course, the relentless forward march of entropy can be combated — shattered glasses can be repaired, messy rooms can be cleaned and organized, and even warm milk can be cooled and preserved — if you no longer have an isolated system, but one where external influences can affect the system in question. This typically takes two forms:

• one where actual matter is transferred into or out of the system, along with heat, energy, and work exchanges also,
• and one where no matter is allowed to enter or leave the system, although energy can still be transferred in-or-out and the boundaries of the system’s physical extent are allowed to change as well.

The first of these gives you the most freedom, and is what’s known as a thermodynamically open system. In an open system, matter is allowed to enter and leave it, along with energy. In an open system, not only are the walls of a system allowed to expand or contract, but the walls aren’t even impermeable: matter can enter or leave it. A pot on a stove is an open system, as energy can enter it (through the burner beneath it) and matter can leave it (by escaping into the air above it), whereas a Dutch oven isn’t completely open, as energy can enter it (through the burner below) but no matter can leave it, as the sealed top confines any matter heated into the gaseous phase.

A pot on a stove, at bottom, represents an open thermodynamic system, as energy can enter the system from below and matter can escape from the system up above. A sealed Dutch oven, at top, represents a closed thermodynamic system, as energy can enter but no matter can leave.

The in-between case: the closed system

This one is very sneaky: what if you don’t allow matter to enter-or-leave, but you allow either energy and/or work to flow, either into or out of the system, from the external environment?

This is what’s known as a closed system: the in-between case between open and isolated. If something is pinging in your brain right now, going “that’s wrong, that’s not what I learned a closed system is,” then congratulations, you’re in the same boat I was in just a few weeks ago. (And yes, I am a PhD physicist who studied this as part of my PhD.)

In some places — primarily in physics courses in the United States — this is a new distinction. Previously, for many of us, “closed” was synonymous with what we defined “isolated” as, up above. In fact, many of us learned, as a shorthand version of the second law of thermodynamics, “the entropy of a closed system can never decrease.” And while it’s true that the entropy of an isolated system can never decrease, only increase or remain the same, the entropy of a closed system can very much decrease: owing either to the input of work or energy, as illustrated by the famous example of Maxwell’s demon.

This illustration shows two sides to a room: a hot one and a cold one, with a demon between them capable of opening and closing a divider between them. If the divider is opened, the gases will mix; if the gases were initially well-mixed, the demon opening-and-closing the divider could sort the room, even for a “closed” system.

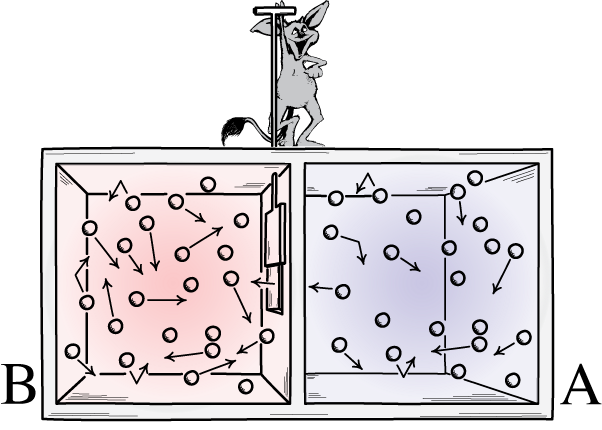
Maxwell’s demon was an idea that said to consider the above system: of a room with a divider in it. Initially, the gases on both sides of the room are what we call “well-mixed,” meaning that both rooms consist of gas that’s:

• composed of the same material on both sides of the divider,
• at the same temperature on both sides of the divider,
• with the same densities on both sides of the divider,
• with no work being done on or by the walls of the container, including the divider,
• and with no energy or heat transfer occurring preferentially in one direction or the other.

But imagine that there’s a little door on the divider separating the two sections of the room, and a tiny little intelligent creature who hates the 2nd law of thermodynamics: a real demon of a character.

Now imagine that this demon is capable of monitoring particles, including whenever a particle attempts to pass through a door in the divider. The demon itself is in control of the door, and sets it up like so:

• Whenever a “cold” particle attempts to pass from the right side of the room to the left, the demon opens the door, letting it (and only it) through before shutting it again.
• Whenever a “hot” particle attempts to pass from the left side of the room to the right, the demon opens the door, letting it (and only it) through before shutting it again.
• And in all other cases, the door remains shut.

What will happen to the particles in the room, assuming we allow the demon to do as it wishes?

A representation of Maxwell’s demon, which can sort particles according to their energy on either side of a box. By opening and closing the divider between the two sides, the flow of particles can be intricately controlled, reducing the entropy of the system inside the box. However, the demon must exert energy to make this happen, and the overall entropy of the box+demon system still increases.

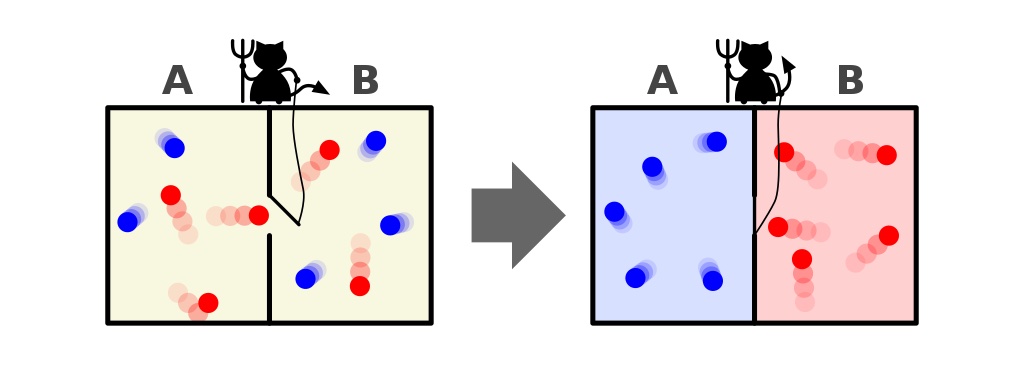
The answer, very clearly, is that we end up with an end-state that’s got a much lower amount of entropy in it: with all the cold particles sorted onto one side of the divider and with all the hot particles sorted onto the other side of the divider, separated from one another.

Did we violate the laws of thermodynamics by decreasing the entropy of this closed system: a system that didn’t allow matter to enter-or-leave it?

No, because we allowed energy to be inputted into the system: in the form of the demon opening and closing the door.

In fact, you can lower the entropy of a system in a variety of ways even if your system isn’t open, but is closed. You can:

• input energy into your system,
• perform work on the boundary of your system,
• allow chemical transitions to liberate energy from within your system,
• pump your system to create a temperature gradient,
• and in general, allow energy to be exchanged between the system and its external environment,

and still obey the second law of thermodynamics. The trick is because the system in question here is only closed: not isolated.

Through the input of energy, and specifically, of work-energy that compresses and rarifies gases in a closed system, a cold reservoir can be made colder and a hot source can be made hotter. This is the key thermodynamic principle behind a heat pump and a refrigerator, and is how modern refrigeration works to this day.

Closed vs. Isolated

This is the key difference that everyone needs to know. In a truly isolated system, there is no interaction, flow, or exchange of matter or energy that occurs between the system you’re considering and its external environment. In a closed system, there are restrictions on the type of exchange that occurs, but some type of energy exchange is still permitted. Even if it’s just the walls of the container of your system expanding or contracting, that’s still an interaction with the environment, as work (a form of energy) is being performed on the container walls, and that work (energy) then has effects on the internal energy of the system being considered.

The key realization that helps put the second law of thermodynamics back into order is this: if you “widen” your view of what your physical system under consideration is, so that it includes both the “closed system” you were examining previously and also the external environment around the closed system, you’re now considering the total system, and that is an isolated system.

In other words, to do proper accounting of all of your entropy, you need to include the changes in entropy that also occur in your (previously-considered-to-be) external environment. If you do that, then you’ll find that the total entropy of your total (isolated) system can never decrease: only increase or remain the same, depending on whether it’s in thermal equilibrium or not.

The difference between an isolated, closed, and open thermodynamic system. In an isolated system, no matter or energy is exchanged between the system and the environment, and entropy can never decrease. In an open system, both exchanges are allowed, whereas for a closed system, only energy, not matter, can be exchanged with the environment. In the case of both a closed and open system, the entropy of the system is allowed to decrease under the proper circumstances.

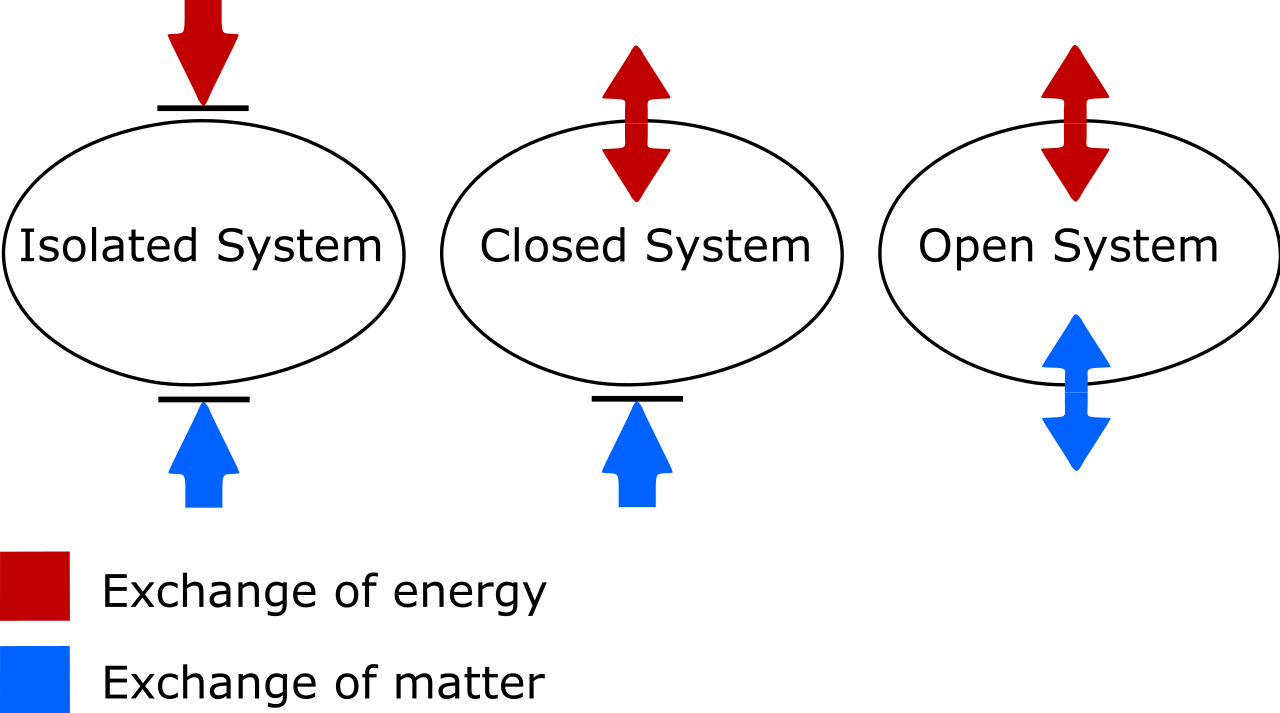
There are two things to look out for here. One is on the important distinction between isolated, closed, and open thermodynamic systems. As someone who’s needed to update my own vocabulary, know that:

• Isolated systems allow no exchange of matter or energy of any type with the environment, including work-induced changes on the boundary of your system. Entropy can never decrease for an isolated system.
• Open systems are free-for-alls, allowing the exchange of matter and energy between the system and the environment, and the entropy can in principle take on any value at all in the end-state due to the allowed exchanges.
• Closed systems allow no exchange of matter/material between the system and the environment, but do allow energy and work to be exchanged across the boundary separating the system from the environment. Entropy can be decreased, under the proper conditions, with sufficient energy input from the environment. (And that if you also consider the external environment in conjunction with your closed system, you can “promote” it to an isolated system, for which entropy can never decrease.)

While there are many open systems that are “approximately” closed when it comes to matter (humans eat, breathe, and excrete matter, but are approximately closed; planets lose atmospheric molecules to space and also receive material via impacts from space, but are approximately closed), the distinction between open, closed, and isolated is of paramount importance when considering the behavior of real, physical systems. In the quest to understand the Universe, it’s important that we all be able to understand the terms we’re using when we talk about these concepts with one another. To everyone who learned physics the same way I did, it’s time to update our knowledge: a closed system only forbids matter exchange, and with the proper input of energy, the entropy of even a closed system really can decrease!