Ask Ethan: What does “Grand Unified Theory” mean?
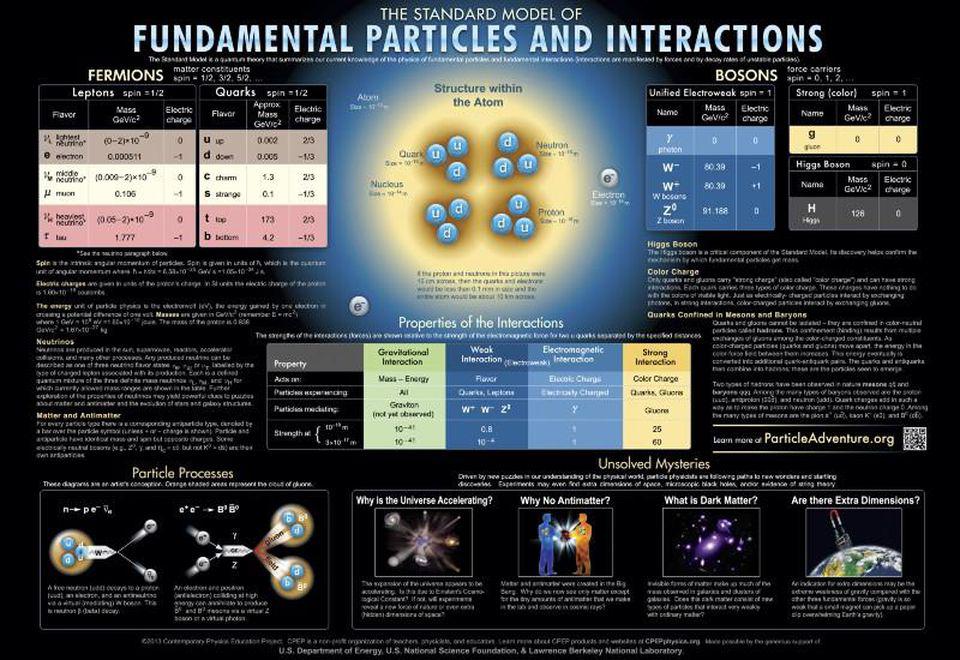
- In the Standard Model of particle physics, excluding gravity, there are three fundamental quantum forces: electromagnetism, plus the strong and weak nuclear forces.
- At high energies, the electromagnetic and the weak forces unify, creating the "electroweak" force. Does that mean, at even higher energies, all the forces unify?
- This idea, of Grand Unification, has been interesting and compelling for nearly 50 years now. Here's how to think about it, even if you don't know the math.
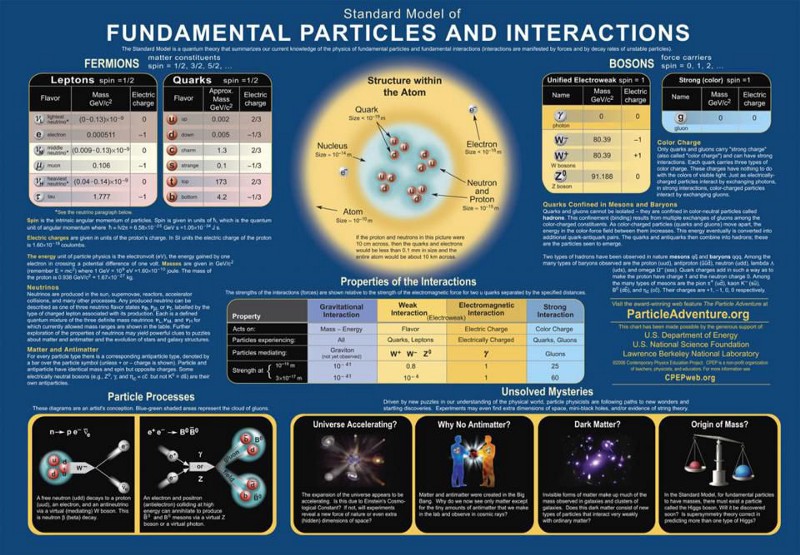
Whenever we think about the Universe at a fundamental level, there’s always the temptation to wonder if reality might somehow be simpler than we perceive it to be. As complex and diverse as the natural world is, it’s humbling to recognize that everything we see, perceive, and interact with is made of the same building blocks. Matter is made of atoms, which are made of protons, neutrons, and electrons; protons and neutrons are further made of quarks and gluons. There are other particles as well: photons, neutrinos, and some heavier cousins of the light quarks and the electrons. Taken all together, everything that cannot be divided further — what we call “fundamental” or “elementary” — makes up the modern Standard Model of elementary particles.
And yet, it’s only natural to wonder if the particles and forces that we know today couldn’t be further simplified, perhaps all emerging from some more unified state that existed early on in the Universe’s history? That’s the question of Patreon supporter Igor Zhbanov, who writes in to ask:
“What [does] the Grand Unified Theory mean in practice? I.e., what does it mean that at the higher energy level we will have only one kind of force? E.g., will we have two balls of energy that will gravitate and electrically attract with the same force value simultaneously? And will we have only one formula for expressing all the physical laws? Or how will the particles behave under this unified force?”
Despite the fact that names like “Grand Unified Theory” or “Grand Unification” sound simple, it’s one of the most difficult ideas in theoretical physics to truly wrap your head around. Let’s explore what it’s all about.
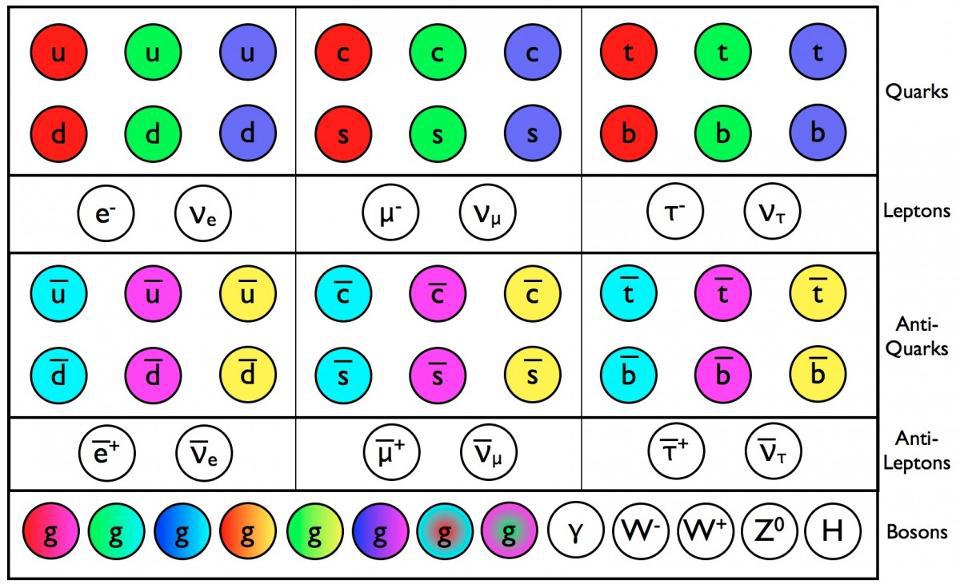
This image, above, shows the Standard Model of elementary particles that has stood for more than 50 years. Back in 2011, the Higgs boson — the final particle that had yet to be detected — revealed itself at the Large Hadron Collider at CERN: the culmination of nearly half-a-century of searching for it. With its discovery, we were finally able to complete the Standard Model, which describes all of the known particles in existence. (Note: the Standard Model does not include dark matter or dark energy; these are still mysteries.)
According to the Standard Model, there are three fundamental forces that it describes.
- The electromagnetic force, which acts on particles that have a fundamental (positive or negative) electric charge to them, and which can be either attractive or repulsive. The photon is the only particle that mediates the electromagnetic force.
- The weak nuclear force, which acts on particles that have a (much less commonly known) property called weak isospin or weak charge. Although it can be either attractive or repulsive, the weak force is much better known for its involvement in radioactive decays, in nuclear fission and fusion, and for changing the flavor (i.e., “type”) of quarks and leptons. There are three particles, the two charged W bosons and the neutral Z boson, that mediate the weak force.
- And the strong nuclear force, which only acts on particles that have a color charge: the quarks and the other gluons, exclusively. The strong force has the odd property of exerting a negligibly small force at very small distances, but of having the force grow very large when the distance between particles increases: a property called asymptotic freedom. It keeps protons and neutrons (and all particles made of quarks and/or antiquarks) bound together, and there are eight gluons that mediate it.

However, these three forces aren’t completely independent of one another. Some particles, like the quarks, can experience all three of these interactions. Other particles, like the electron, muon, and tau, can only experience the electromagnetic and weak nuclear forces. Still others, like the neutrinos, can only experience the weak force, while the photon can only experience the electromagnetic force. This overlap is why we don’t simply have three separate theories for the three fundamental forces, but rather one overarching theory — the Standard Model — that explains how all of them work in cahoots with one another.
One of the important realizations that occurred in the early 1960s was the realization that the electromagnetic force and the weak force couldn’t be described as completely independent of one another, but rather that there’s an interplay between the two of them. You cannot just explain the weak force with weak isospin and the electromagnetic force with electric charge, but rather there needs to be a new quantum number that ties the two of them together: weak hypercharge, which was first introduced by Shelly Glashow in 1961.
When particle physicists talk about the Standard Model, they normally do so in the context of group theory. You might have noticed that the Standard Model contains:
- 1 boson mediating the electromagnetic interactions,
- 3 bosons mediating the weak interactions,
- and 8 bosons mediating the strong interactions,
and you might have noticed what could be the hint of a pattern there. The number 3 happens to be 22 – 1, and the number 8 happens to be 32 – 1. This is no coincidence, and can be explained in the context of group theory.
Two of the most common properties of groups are orthogonality, O, which is a mathematical property that corresponds to the operation of how objects rotate, and unitarity, U, which is a mathematical property that corresponds to the operation of matrix multiplication. If you ask, “how many elements do you need to describe a unitary group?” the answer depends on the size of the matrix. If the matrix is a 1 × 1 matrix, U(1), you need 1 element. If it’s 2 × 2, U(2), you need 4 elements. If it’s 3 × 3, U(3), you need 9 elements.
And if the matrix has a special property — that its mathematical determinant is 1 — that’s an additional restriction: that takes one of the elements away. So if your 2 × 2 matrix isn’t just a unitary group but is a special unitary group, SU(2), you only need 3 elements, not 4. And if your 3 × 3 matrix isn’t just a unitary group but a special unitary group, SU(3), you only need 8 elements, not 9.

Just from this, you might anticipate that, quite possibly, the Standard Model would have the structure of being a 3 × 3 special unitary matrix for the strong interactions, a 2 × 2 special unitary matrix for the weak interactions, and a 1 × 1 unitary matrix for the electromagnetic interactions.
We would write this as SU(3) ⊗ SU(2) ⊗ U(1), and identify the SU(3) part with the strong interactions, the SU(2) part with the weak interactions, and the U(1) part with the electromagnetic interactions.
This is close! The problem with this interpretation is that we know that the electromagnetic and the weak components of the Standard Model overlap, and cannot be separated out cleanly. (This was the point of needing weak hypercharge, as Glashow showed!) So the U(1) part can’t be purely electromagnetic, and the SU(2) part can’t be purely weak; there has to be mixing in there. That’s part of why we say that it’s the electroweak force, and that those two groups need to work together: SU(2) ⊗ U(1), to describe the electroweak interaction. If we describe things in this fashion, we get the Standard Model as we know it, and the mathematics allows us to assign particles based on the properties that they’re predicted to have.
The fact that every particle that’s been predicted exists and has been verified to have the properties that they do is a tremendous success for the Standard Model, and why all alternatives have fallen by the wayside.
But it’s only natural to wonder about a few questions, starting with: is the Standard Model all there is, or might there be some greater underlying symmetry that would become apparent at much higher energies? Are there new particles and new interactions, and therefore, new physical phenomena that have yet to be detected, out there? And if so, what sort of structure, including in the context of group theory, does it possess?
That’s where the idea of a grand unified theory, known as either a GUT or as grand unification in concept, comes from. The starting point is the Standard Model, which in group theory format is SU(3) ⊗ SU(2) ⊗ U(1). It then teaches us to look for a larger group that contains the Standard Model, but which embeds the Standard Model into some grander structure with a higher degree of symmetry. This structure, necessarily, also includes additional particles and/or additional couplings, and also brings along with it new predictions, as processes that are either suppressed or outright forbidden in the Standard Model will be permitted, and therefore compulsory, in these grand unified theories.
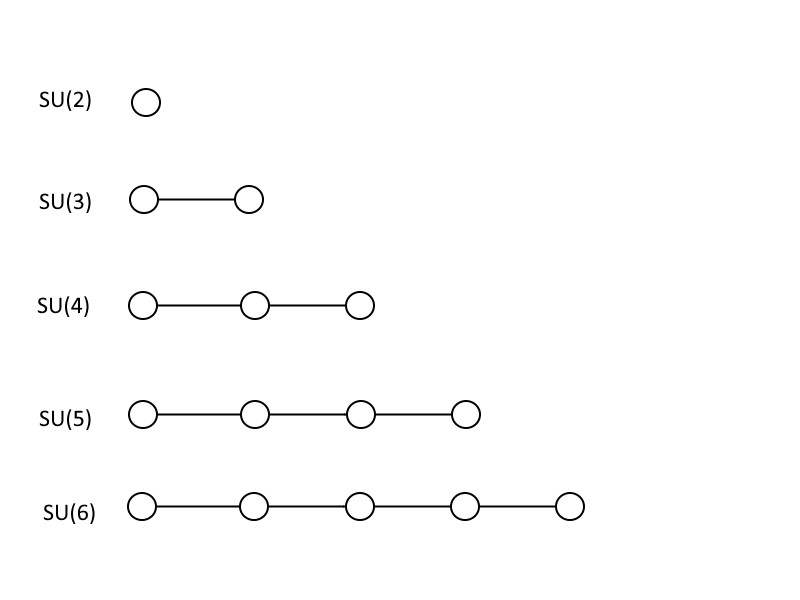
To show you how grand unified theories work, I’m going to teach you a little bit of math, although unless you’re either a mathematician or a physicist, you might not even recognize it as math. The pictures, above, which look like circles connected by lines, are known as Dynkin diagrams. If you have one circle by itself, that corresponds to SU(2), which is a 2 × 2 matrix with a determinant of 1. If you have two circles connected to one another, that’s SU(3): a 3 × 3 matrix with a determinant of 1. You can keep adding circles and connecting them in the same fashion, where the number of connected circles plus one tells you the size of your matrix, and hence the size of your special unitary group. The Standard Model contains one SU(3), one SU(2), and a U(1), where the last one doesn’t get a symbol in the world of Dynkin diagrams.
Another kind of group that shows up a lot in grand unification is the special orthogonal, SO, set of groups. Instead of circles just connected by a single line in a chain, the Dynkin diagram for the (even-numbered) special orthogonal groups have a “branched” structure, where the penultimate “circle” doesn’t just connect to the last one on the end, but has an extra circle coming off of it.
SO(6), as you can see below, has the same-structured Dynkin diagram as SU(4), but every other diagram is uniquely different, where the number inside the parenthesis is always double the number of circles. Once you get the pattern, it’s pretty easy to see that you can build both your SU(n+1) and your SO(2n) groups as large as you want, with no limit.

But we don’t need to get arbitrarily large; we just need to get large enough that we can embed the entire Standard Model within our group.
How do we figure that out?
Here’s a very useful rule when it comes to the math of Dynkin diagrams: every time you erase a “circle” from your diagram, you also erase the lines that connect it to the other circles, and each erasure can also get you a “bonus” U(1) group that comes along for free.
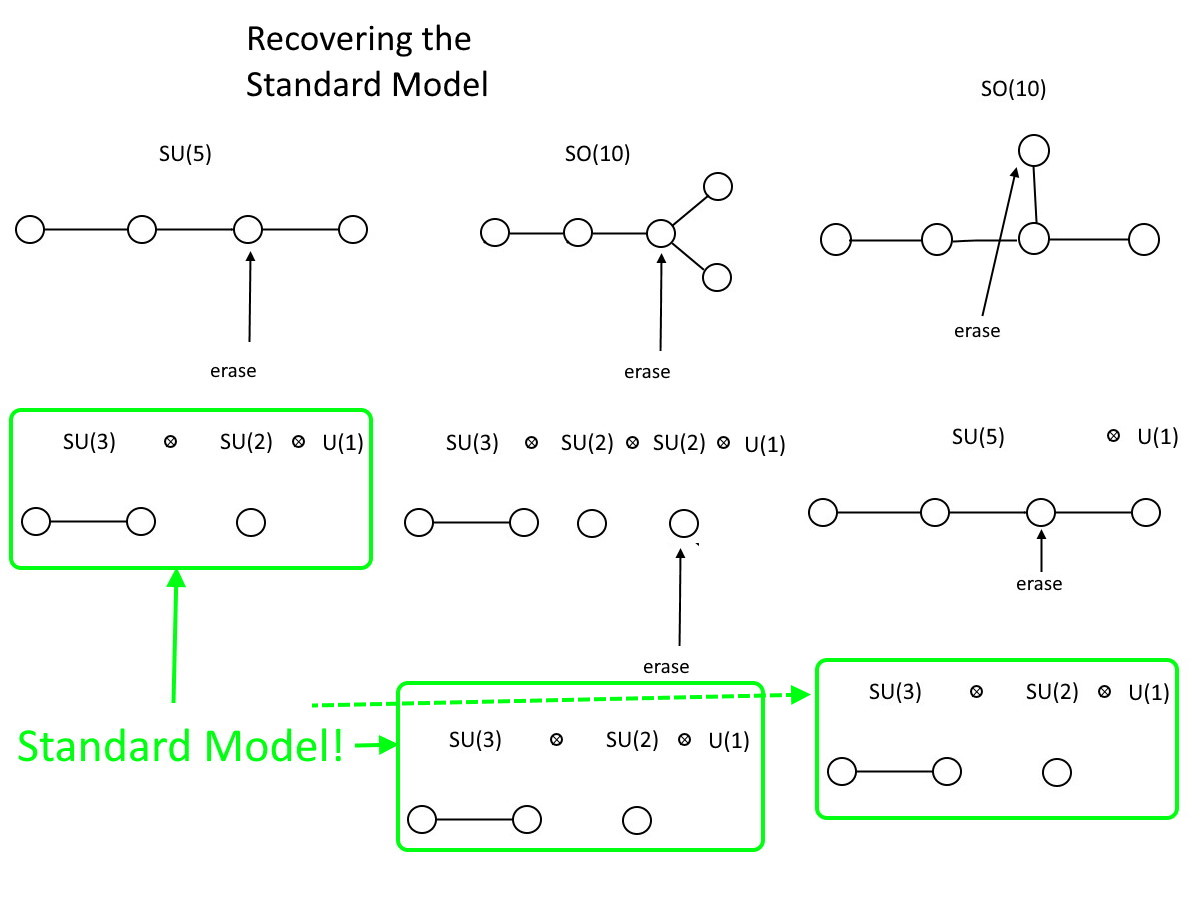
So if we wanted to embed the Standard Model, which is SU(3) ⊗ SU(2) ⊗ U(1), into a larger group, what’s the minimum-sized group we’d need to do it?
On the special unitary side, SU(5) will do it. If you have four circles connected by (three) lines, then all you need to do is erase one of the middle two circles. Where you’re left with two circles connected by a line, that’s SU(3). Where you have a single circle left isolated by itself, that’s SU(2). And you also get a “free” U(1) out of the act of erasing, so there it is, your Standard Model: SU(3) ⊗ SU(2) ⊗ U(1).
On the special orthogonal side, meanwhile, the smallest group that will hold the Standard Model is a little bigger: SO(10). As you can see, SO(10) can not only contain the Standard Model, but can also contain SU(5) within it. In this instance, you have to erase two circles to recover the Standard Model, and you can choose which order you erase them in. But either way, you have to “get rid” of an extra U(1) group to wind up with the Standard Model and erase two circles instead of one; SO(10) is a larger group than SU(5) is, and SU(5) is larger than the Standard Model.
A larger group that contains a smaller group (or set of smaller groups) will always contain all of the particles that are present in the smaller group, plus additional ones. In the Standard Model, one of the more puzzling aspects of reality that we’re faced with is that the Universe is not symmetric in a number of ways. In particular:
- the Fermions are chiral, meaning there are differences between “left-handed” and “right-handed” quarks and leptons,
- there are only “left-handed” neutrinos and “right-handed” antineutrinos; never any “right-handed” neutrinos or “left-handed” antineutrinos,
- and that the weak interaction, particularly through the W-bosons, only couple to the left-chiral fermions, not the right-chiral ones.
The SO(10) group, however, is left-right symmetric, which you can see explicitly if you “break” the symmetry in the middle column, as shown above. In the Standard Model, we sometimes write SU(2) with an “L” as a subscript attached to it, to remind ourselves that we live in a chiral Universe. If, however, we break SO(10) by erasing the circle with three connections, we recover not just the Standard Model, but a left-right symmetric model: SU(3) ⊗ SU(2) ⊗ SU(2) ⊗ U(1), where one SU(2) would have an “L” and the other one would have an “R” attached to it.
Over on the SU(5) side, however, you wind up with a 5 × 5 matrix with 24 unique elements, instead of SU(3) ⊗ SU(2) ⊗ U(1), which has far fewer. As a result, you wind up predicting extra particles, known either as X bosons or X-and-Y bosons, depending on terminology, and extra allowable interactions that they mediate. In particular, they allow extra couplings between quarks and leptons, and — in stark disagreement with observations — they predict that the proton itself would be fundamentally unstable.
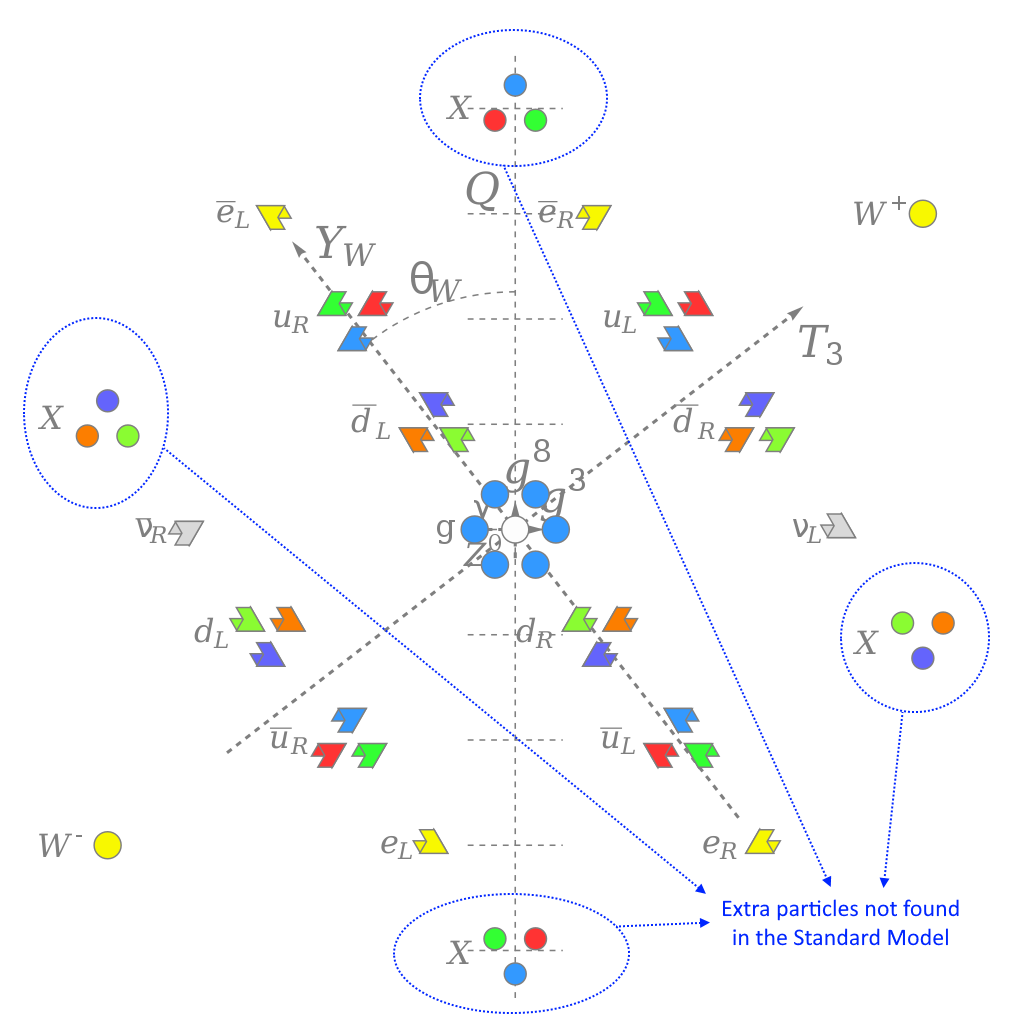
Anything that’s found in a smaller group that can be embedded within a larger one will always exist in the larger one, so all grand unified theories that contain SU(5) or SO(10) or anything larger will also contain these X (or X-and-Y) bosons, and will predict proton decay. The better we constrain the lifetime of the proton, the better we can constrain these models. SU(5) was originally interesting because it predicted proton decay with a lifetime of ~1030 years; modern constraints tell us that the proton’s lifetime is greater than about 1034 years today, ruling simple SU(5) unification out. If we can get that number up to about 1036 to 1037, we may rule out SO(10) as well.
However, one of the reasons that grand unification has remained so compelling to theorists is its connection to string theory. In string theory, particles can be viewed as “excitations” that move either counterclockwise (leftward) or clockwise (rightward), where one corresponds to a bosonic string moving in 26 dimensions and the other corresponds to a superstring moving in 10 dimensions. You need a mathematical space with exactly 16 dimensions to account for the mismatch, and the two known groups with the right properties to save the day are SO(32), which is enormous, and E(8) ⊗ E(8),* which is equally enormous. Although we haven’t talked about the (exceptional) E groups, I did want to show them, below, and to note that there are only three of them: E(6), E(7), and E(8). (There are two other exceptional groups as well, F(4) and G(2), but they have different structures.)
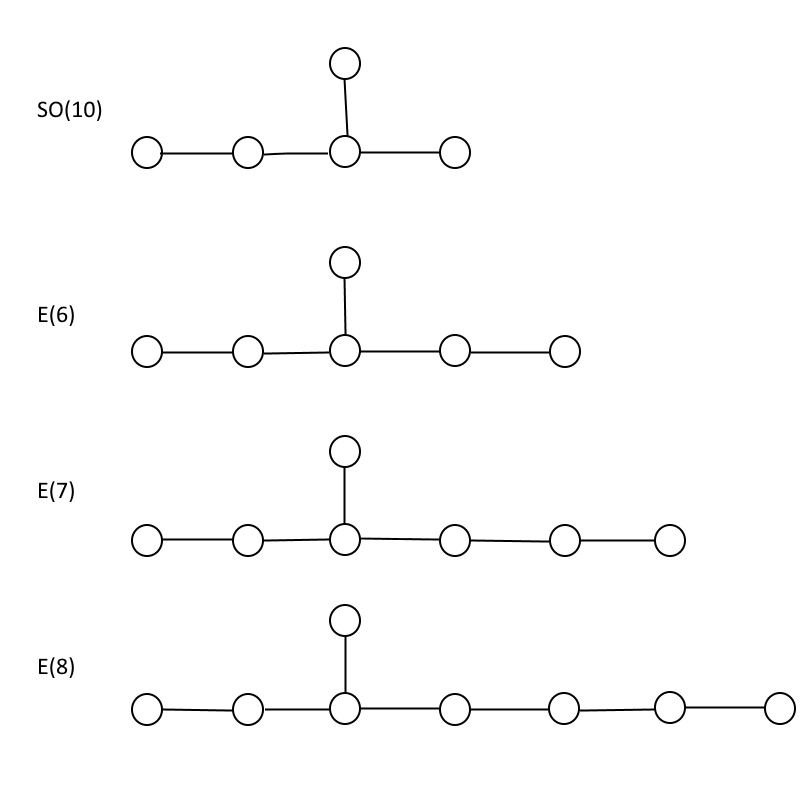
You might wonder, if you can “branch” from the next-to-last circle in an SU group to create an SO group, and if you can extend one of the “short” branches in an SO group to create an E group, why couldn’t you either create additional branches or extend more branches by greater amounts?
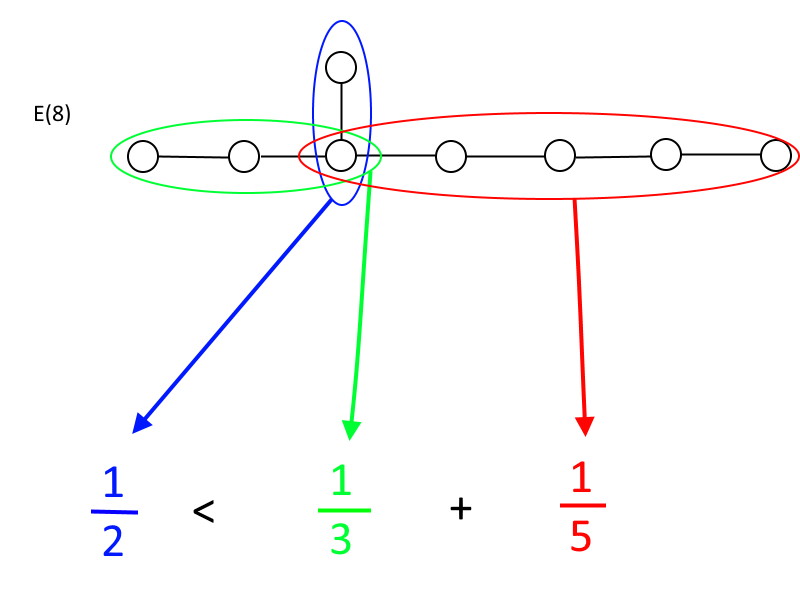
Well, there’s a simple mathematical rule that prevents you from doing so and still meeting the requirements of a “group.”
If you start at any circle where more than two lines come off from it, there’s a relationship you have to obey in order to be a group. In each direction, you’ll have a certain number of circles that are connected by lines: call them A, B, and C, where A is always going to be the one with the fewest number of circles. The rule is this: only if 1/A is smaller than 1/B + 1/C are you a group. If 1/A is greater than or equal to 1/B + 1/C, you’re no longer a group. As you can swiftly verify, only E(6), E(7), and E(8) meet those requirements, with E(8) being the largest exceptional group allowed.
The takeaway from all of this is that the Universe, if grand unification is a real thing, actually is more complicated, with more particles and interactions, than the Standard Model presently dictates. One of the things that absolutely must occur if our Universe is described by a grand unified theory is that the proton must not be stable, but rather will decay with some finite lifetime. Another bizarre prediction is that there should be new hypothetical particles that have properties of both quarks and leptons at the same time: leptoquarks.
Back in 1997, the HERA accelerator in Germany produced an excess of events that appeared to be consistent with the presence of leptoquarks, triggering a resurgent interest in grand unified theories. However, additional data, including at Fermilab’s Tevatron and later, at the Large Hadron Collider, ruled this possibility out at all energies achievable by HERA. As it stands today, the idea of grand unification remains theoretically compelling, but the evidence for it is non-existent. After all, the key to science is always this: if it disagrees with experiment, it’s wrong. We haven’t ruled out the possibility that there is some sort of unification that occurs at extremely high, yet-to-be-accessed energies, but with each null result, the tighter the constraints on GUTs become.
* – Normally, exceptional groups are written with the number as a subscript rather than in parentheses. This article has written them in parentheses to simplify the notation for those who are new to group theory and Dynkin diagrams.
Send in your Ask Ethan questions to startswithabang at gmail dot com!