Ask Ethan: How does Hawking radiation lead to black hole evaporation?
- Black holes are the densest objects in all the Universe, with so much mass in one location that space becomes so severely curved that no signals, not even light, can escape.
- But in 1974, Stephen Hawking showed that a set of quantum processes, when combined with the background spacetime surrounding a black hole, causes them to evaporate.
- The consequence, black hole evaporation, and the underlying process of Hawking radiation, are so poorly understood that even Hawking explained it incorrectly. Here's what happened instead.
It’s truly a marvel how quickly our understanding of the Universe advanced during the 20th century. At the start of the 1900s, we were only beginning to uncover the quantum nature of reality, hadn’t yet moved beyond the confines of Newtonian gravity, and had no notion of the existence of astrophysical objects like black holes. By the arrival of the 1970s, we had progressed to a General Relativity-governed Universe that began with a hot Big Bang, filled with galaxies, stars, and stellar remnants, where the Universe was fundamentally quantum, described remarkably accurately by what’s now known as the Standard Model.
And in 1974, Stephen Hawking put forth a revolutionary paper that taught us that black holes wouldn’t live forever, but rather would evaporate by an inherently quantum-and-relativistic process, now named Hawking radiation. But how does it occur? That’s what Ralph Welz wants to know, asking:
“I thought I had understood it: At the border of the event horizon, [an] electron and positron [pair] is created for a short moment [via] the Uncertainty Principle. The electron just escapes, the positron is sucked-in… and voila there is an electron mass vanished from the black hole. But now [hasn’t] the black hole fattened by another positron mass? Where is my misunderstanding?”
It’s hard to fault you for this misunderstanding. After all, if you read Hawking’s famous book, A Brief History of Time, this is how he — incorrectly, mind you — explains it. So what’s the actual truth?

Let’s start with the very notion of a physical black hole itself. There are a few ways to form a black hole:
- from direct collapse of a large amount of gas,
- from the core collapse of an extremely massive star,
- from matter accretion onto a dense stellar remnant that leads to a breakdown of the nuclear structure of matter,
- or from the merger of two neutron stars,
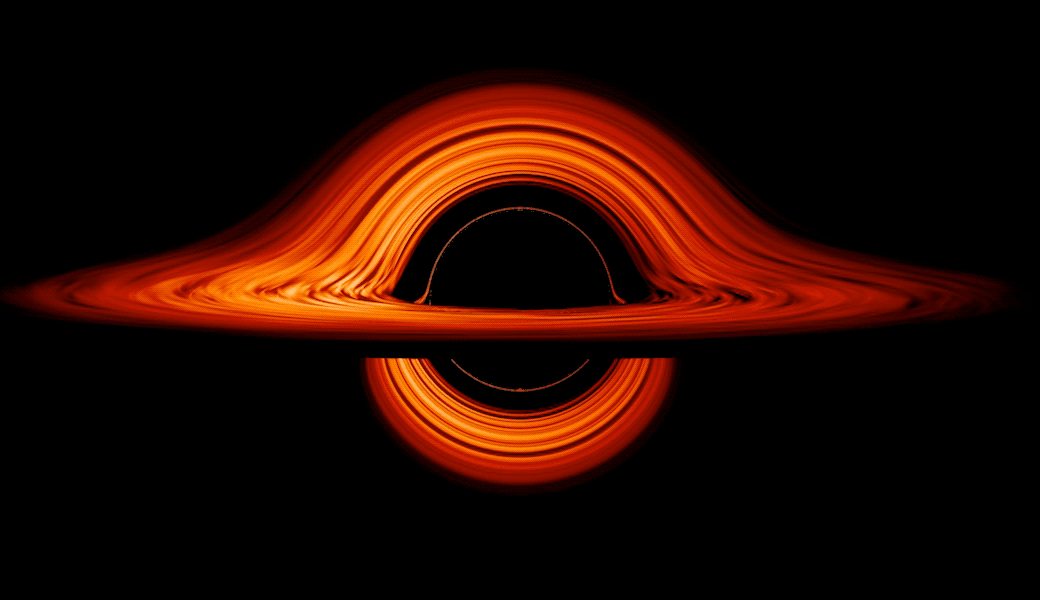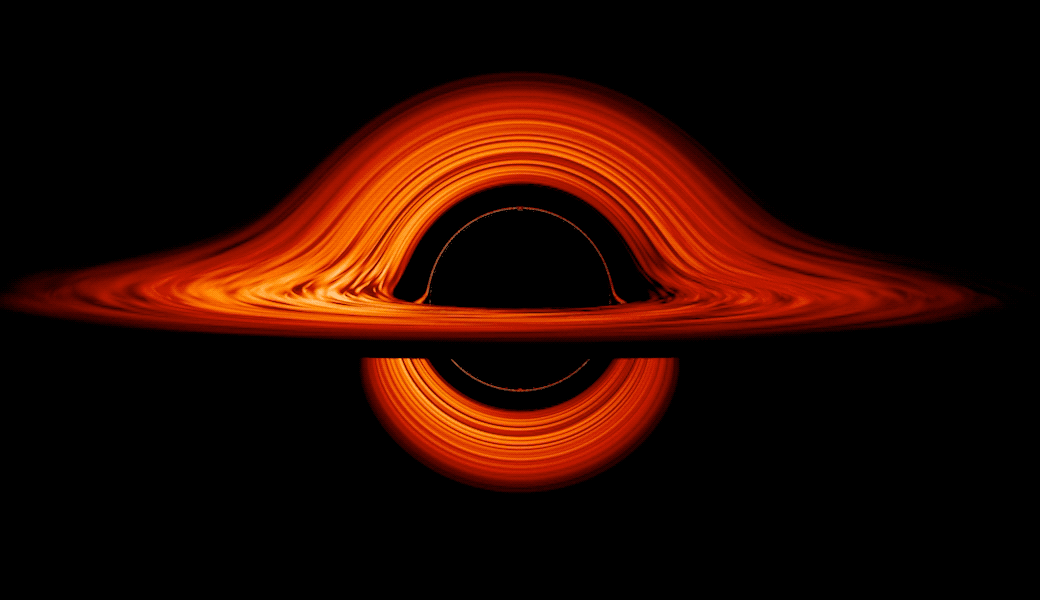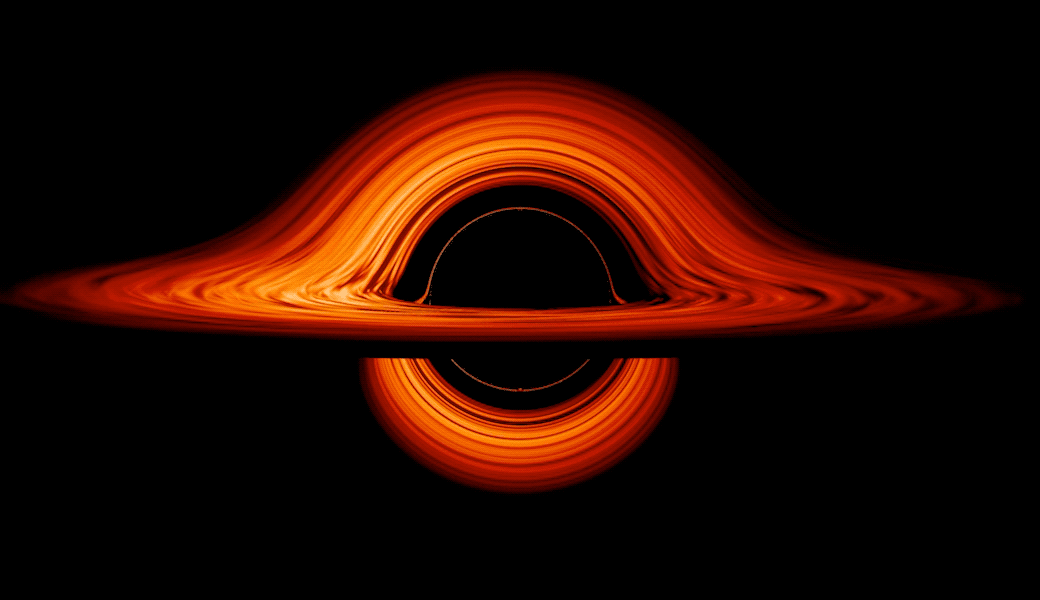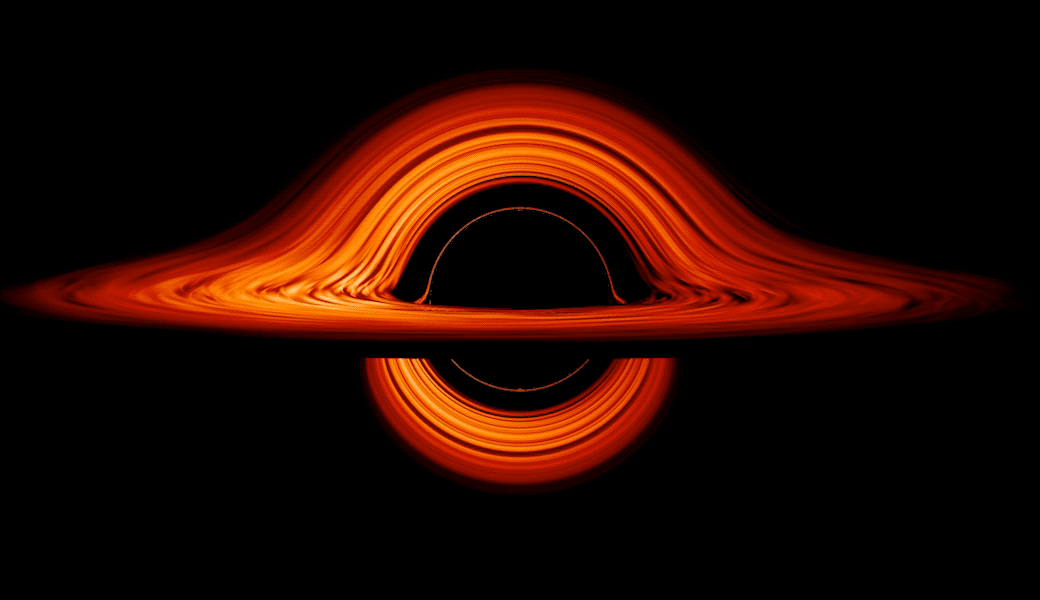
among others. Once enough mass is gathered together into a small enough volume, an event horizon forms. Within that event horizon, no signals can ever propagate outward beyond it, not even if they move at the maximum allowable speed within the Universe: the speed of light.
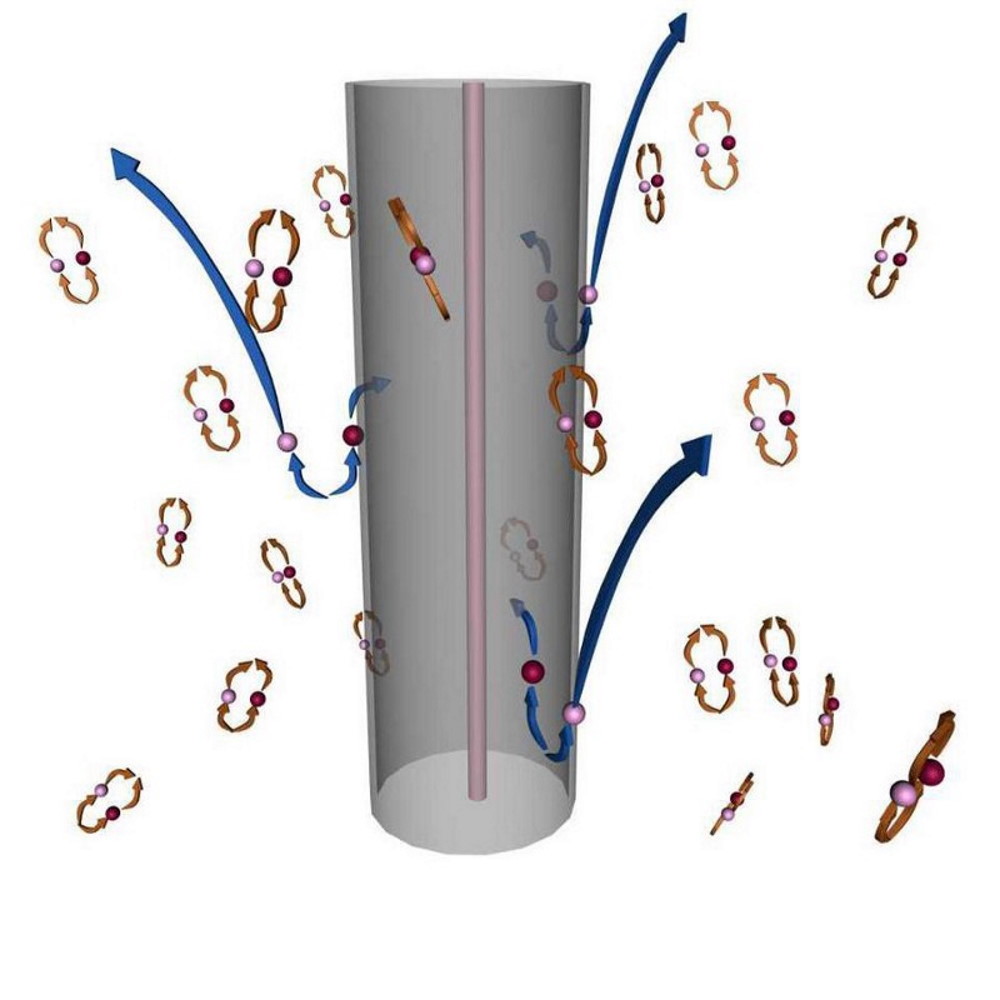
From outside the black hole, anything that crosses over the event horizon will inevitably be drawn into the central singularity. But any object outside the black hole, given enough energy and/or speed (in the right direction), has the possibility of escaping its gravitational pull after all. This includes real particles like photons, electrons, protons, and more, of course. But in a quantum Universe, there are also quantum fields that exist throughout all of space, even near the border of the event horizon itself. One common visualization of the fluctuations in these quantum fields is the spontaneous creation of particle-antiparticle pairs, which take advantage of the energy-time uncertainty relation to briefly create these entities over extremely short periods of time.
These field fluctuations are very real, and occur even in the absence of any “real” particles. In the context of quantum field theory, the lowest-energy state of a quantum field corresponds to no particles existing. But excited states, or states that correspond to higher-energies, correspond to either particles or antiparticles. One visualization that’s commonly used is to think about empty space as being truly empty, but populated by particle-antiparticle pairs (because of conservation laws) that briefly pop into existence, only to annihilate away back into the vacuum of nothingness after a short while.
It’s here that Hawking’s famous picture — his grossly incorrect picture — comes into play. All throughout space, he asserts, these particle-antiparticle pairs are popping in and out of existence. Inside the black hole, both members stay there, annihilate, and nothing happens. Far outside of the black hole, it’s the same deal. But right near the event horizon, one member can fall in while the other escapes, carrying real energy away. And that, he proclaims, is why black holes lose mass, decay, and that’s where Hawking radiation arises from.

That was the first explanation that I, myself a theoretical astrophysicist, ever heard for how black holes decay. If that explanation were true, then that would mean:
- Hawking radiation was composed of a 50/50 mix of particles and antiparticles, since which member falls and which one escapes will be random,
- that all of the Hawking radiation, which causes black holes to decay, will be emitted from the event horizon itself, and
- that every quantum of Hawking radiation that’s emitted by the black hole must possess a tremendous amount of energy: enough to escape from the incredible gravitational pull of black hole from just outside the event horizon.
Remarkably, every single one of these three points are untrue. Hawking radiation is made almost exclusively of photons, not a mix of particles and antiparticles. It gets emitted from a large region outside the event horizon that extends for about ~10-20 times the radius of the event horizon, not merely right at the surface. And the individual quanta emitted have tiny kinetic energies that span several orders of magnitude, not large, nearly-identical energy values.

Why Hawking chose this incredibly flawed, erroneous analogy is a secret he took to the grave with him. It’s an odd choice, given that it has nothing to do with the actual (correct) explanation he gave in the scientific papers that he wrote. If one follows this incorrect explanation, you get the wrong type of particles emitted, the wrong spectrum for their energy, and the wrong location for where you can find the emitted particles. In addition, in perhaps an even greater offense, it has led generations of laypersons and physicists alike to think incorrectly at the process underlying Hawking radiation. Too bad, because the actual scientific story, although slightly more complicated, is far more illuminating.
Empty space really does have quantum fields all throughout it, and those fields really do have fluctuations in their energy values. There’s a germ of truth in the “particle-antiparticle pair production” analogy, and it’s this: in quantum field theory, you can model the energy of empty space by adding up diagrams that include the production of these particles. But it’s a calculational technique only; the particles and antiparticles are not real but are virtual instead. They are not actually produced, they do not interact with real particles, and they are not detectable by any means.
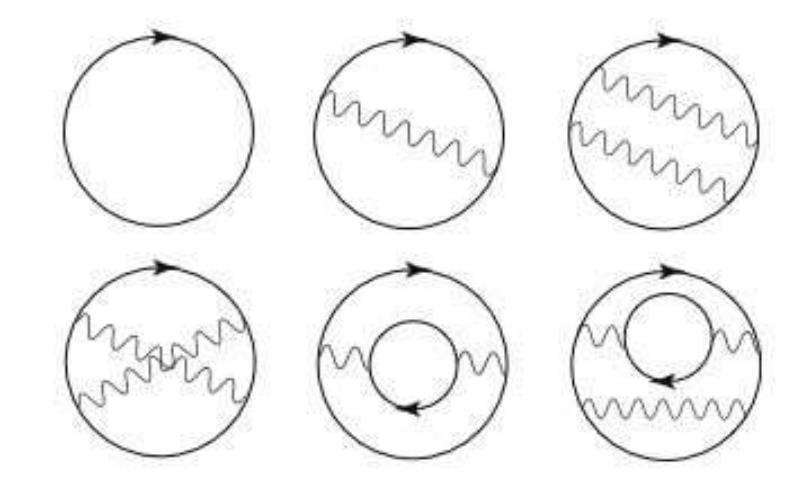
The same laws of physics, governed by the same equations and the same fundamental constants, apply at every single location and at every moment in time, equally, all across the Universe. Therefore, to any observer within the Universe, that “energy of empty space” arising from these quantum fields, which we call the zero-point energy, will appear to have the same value no matter where they are. However, one of the rules of relativity is that different observers will perceive different realities between themselves and others. In particular:
- observers in relative motion to one another,
- and observers in regions of space where the spacetime curvature differs,
will disagree with one another concerning properties of space and time.
If you’re infinitely far away from every source of mass in the Universe, if you’re not accelerating, and your spacetime curvature is negligible, you’ll experience a certain zero-point energy. If someone else is located at a black hole’s event horizon but is in free-fall, they’ll have a certain zero-point energy that they’ll measure to have the same value that you did when you were infinitely far away from that event horizon. But if the two of you try to reconcile your measured value with one another, mapping your zero-point energy to their zero-point energy (or vice versa), the two values won’t agree. From one another’s perspectives, the zero-point energy of empty space is different between the two locations, dependent on how severely the two spaces are curved relative to one another.

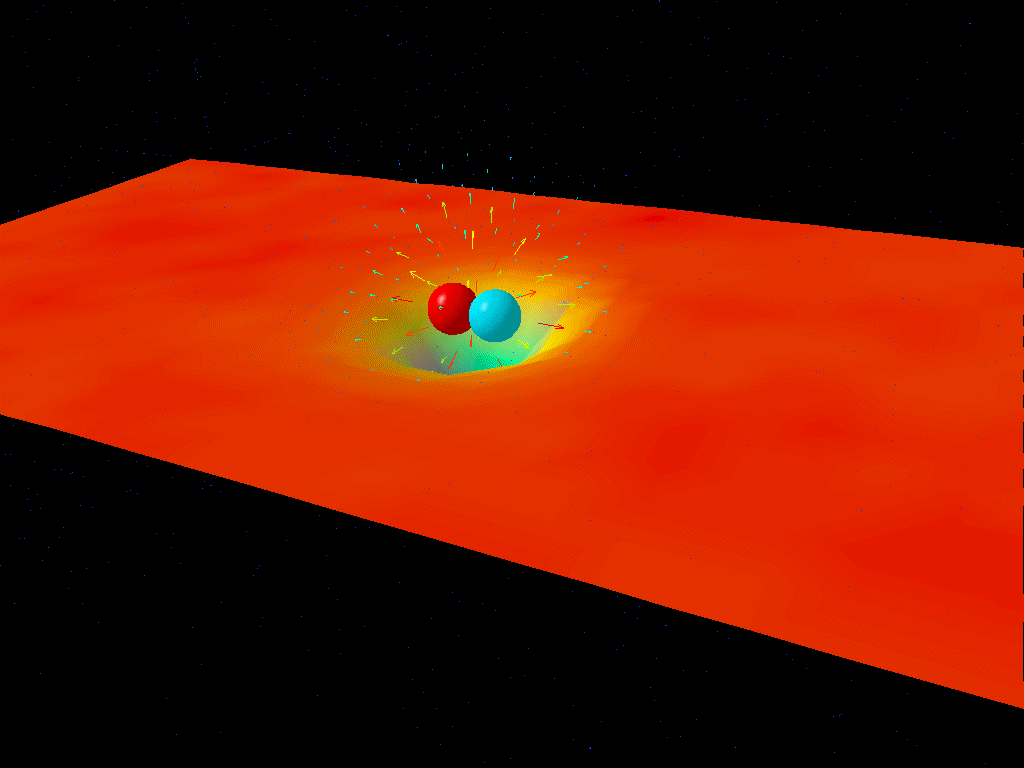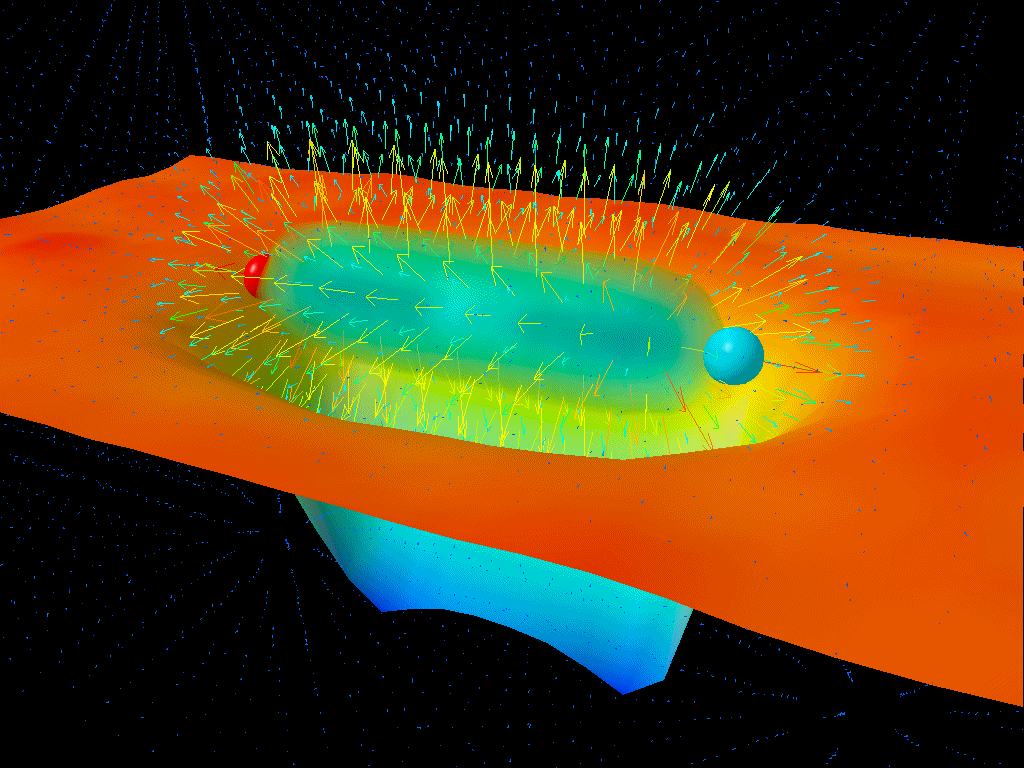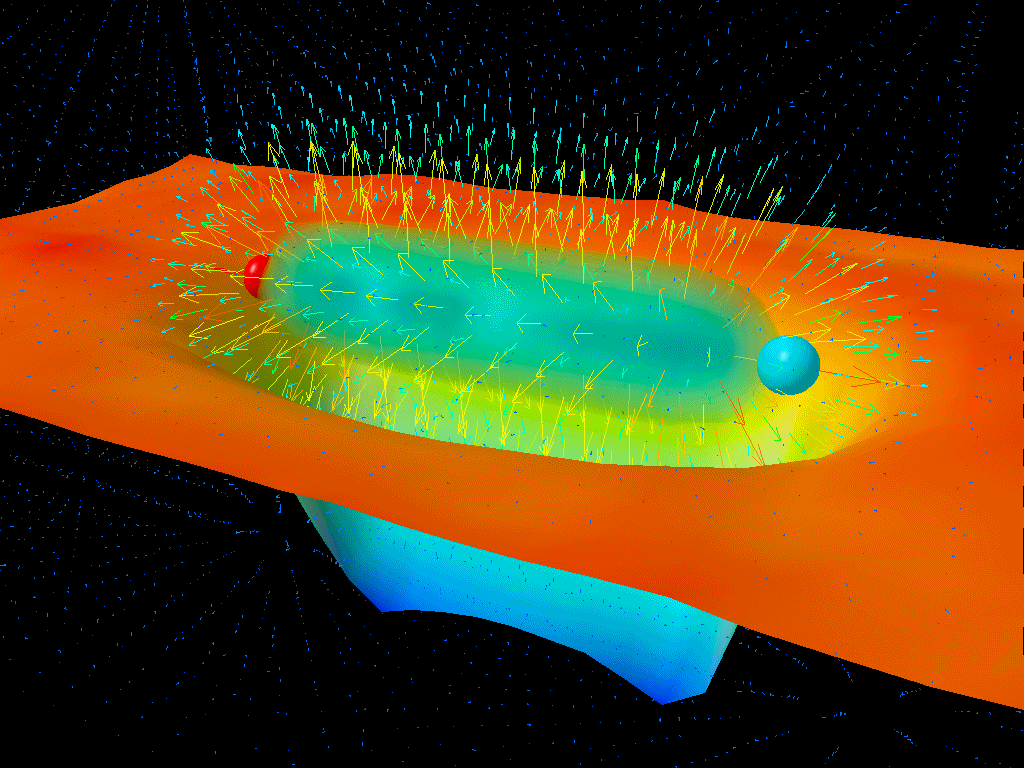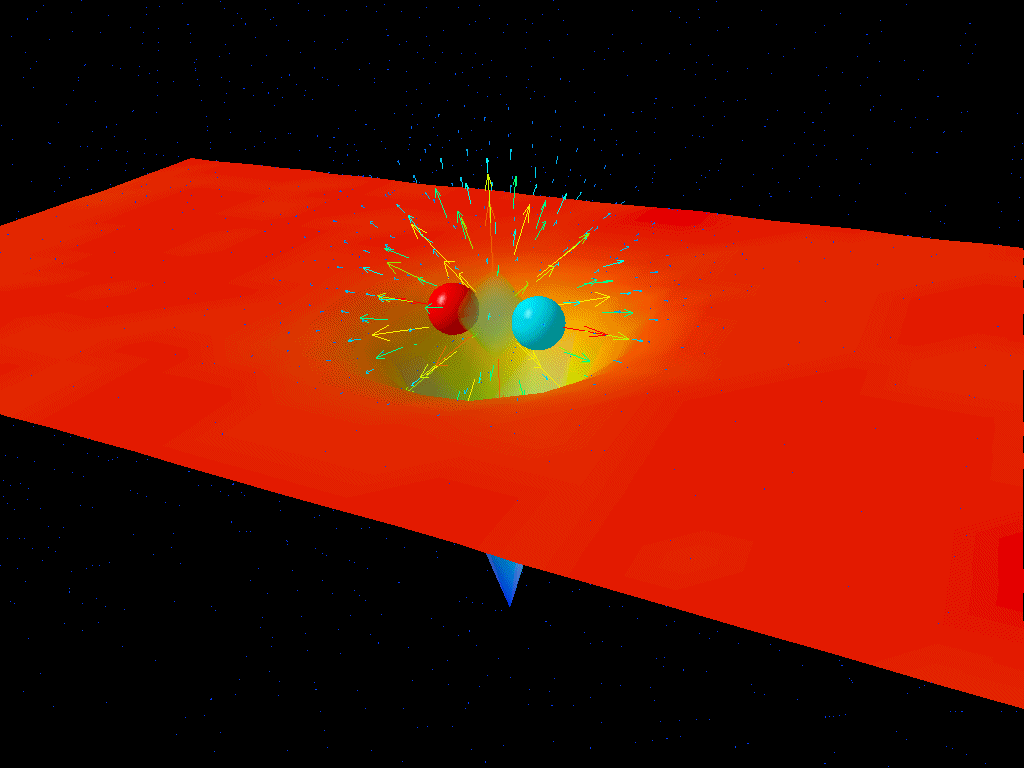
That’s the key insight behind Hawking radiation, and the key calculation that needed to occur in order to derive Hawking radiation. Quantum field theory calculations are normally performed under the assumption that the underlying space is flat and uncurved, which is usually an excellent approximation, but not so near the event horizon of a black hole. Stephen Hawking himself knew this, and in 1974, when he famously derived Hawking radiation for the first time, this was exactly the calculation he performed: calculating the difference in the zero-point energy in quantum fields from the curved space around a black hole to the flat space infinitely far away.
The results of that calculation allow one to determine the properties of the radiation that emanates from a black hole.
- The radiation arises not from the event horizon exclusively, but from the entirety of the curved space around it.
- The temperature of the radiation becomes dependent on the mass of the black hole, with higher-mass black holes producing lower-temperature radiation.
- This calculation predicts the spectrum of the radiation: a perfect blackbody, indicating the energy distribution of photons and — if there’s enough energy available via E = mc² — massive particles and antiparticles, such as neutrinos/antineutrinos and electrons/positrons, too.

That first point is particularly underappreciated: that Hawking radiation doesn’t exclusively originate from the black hole’s event horizon itself, but rather from within an extended region around the black hole where the curvature of space is significantly different from flat, uncurved space. While most pictures and visualizations show 100% of a black hole’s Hawking radiation being emitted from the event horizon itself, it’s more accurate to depict it as being emitted over a volume that spans some 10–20 Schwarzschild radii (the radius to the event horizon), where the radiation gradually tapers off the farther away you get.
This type of radiation arises wherever you have a horizon; not only around the event horizons of black holes. As a spectacular example, the Universe possesses a cosmological horizon: a region where, beyond a certain point, access is cut off owing to the expansion of the Universe. Because of the presence and properties of dark energy, there will be a continuous amount of thermal radiation emitted from the perspective of any stationary observer. Even arbitrarily far into the future, this implies that the Universe will always be filled with a tiny amount of blackbody radiation, peaking with a minuscule temperature of 10-30 K.

The core of the problem with Hawking’s “particles and antiparticles spontaneously pop in-and-out of existence” explanation, an oversimplified explanation of his own theory, is that he conflates what’s useful as a calculational tool with something that actually exists as part of our physical reality. The radiation emitted from the vicinity of a black hole exists; particle-antiparticle pairs that are ripped out of the quantum vacuum do not. There are no virtual particles (or antiparticles) with negative energy falling into the black hole; in fact there aren’t any real, massive particles being emitted as part of Hawking radiation until the black hole is nearly completely evaporated, and sufficiently high energies exist to allow their production. When they do, particles and antiparticles should be created in equal numbers, with the laws of physics not appearing to prefer one type over the other.
What’s really happening is that the curved space around the black hole is constantly emitting radiation due to the curvature gradient around it, and the source of that energy is the black hole itself. As a result, the black hole’s event horizon slowly shrinks over time, increasing the temperature of the emitted Hawking radiation in the process.

Black holes are not decaying because there’s an infalling virtual particle carrying negative energy; that’s another fantasy devised by Hawking to “save” his insufficient analogy. Instead, black holes are decaying, and losing mass over time, because the energy emitted by this Hawking radiation is slowly reducing the curvature of space in that region. Once enough time passes, and that duration ranges from approximately 1068 to 10103 years for black holes of realistic masses, these black holes will have evaporated entirely.
It’s definitely true that spacetime is curved, quite severely, just outside the event horizon of a black hole. It’s also true that quantum uncertainty is an intrinsic part of our Universe’s existence. But Hawking radiation is not the emission of particles and antiparticles from the event horizon. It does not involve an inward-falling pair member carrying negative energy. And it shouldn’t even be exclusive to black holes. Hawking himself knew all of this, but chose the explanation he did anyway, and now we all have to live with the consequences of that decision. Nevertheless, the physical truth always wins out in the end, and now you know the fuller, truer story of where the radiation that causes black holes to evaporate comes from!
Send in your Ask Ethan questions to startswithabang at gmail dot com!