Hawking radiation isn’t just for black holes, study shows

One of the most remarkable achievements in theoretical physics came in 1974, when Stephen Hawking demonstrated that black holes are not static, stable entities within spacetime, but rather must emit radiation and eventually decay. This radiation, known forever after as Hawking radiation, arises due to the combination of the facts that:

• quantum fields permeate all of space,
• including inside and outside a black hole’s event horizon,
• that these fields are not static but exhibit quantum fluctuations,
• and that those fields behave differently in regions where the curvature of spacetime is different.

When Hawking first put these facts together, his calculation showed that black holes can’t be stable with a constant mass, but will instead emit an omnidirectional amount of extremely low-temperature blackbody radiation. This radiation propagates away from the event horizon, and since real radiation carries energy, the only place where that energy can be taken from is from the mass of the black hole itself: via the classic equation E = mc², where the mass lost by the black hole has to balance the energy of the emitted radiation.

But in a delightful new paper, physicists Michael Wondrak, Walter van Suijlekom, and Heino Falcke have challenged the idea that an event horizon is necessary for this radiation. According to their new approach, this radiation arises solely because of the differences in the quantum vacuum of space dependent on its curvature, and therefore Hawking radiation should be emitted by all masses in the Universe, even those without event horizons. It’s a remarkable idea and one that’s been brewing for a long time. Let’s unpack why.

A visualization of QCD illustrates how particle-antiparticle pairs pop out of the quantum vacuum for very small amounts of time as a consequence of Heisenberg uncertainty. The quantum vacuum is interesting because it demands that empty space itself isn’t so empty, but is filled with all the particles, antiparticles, and fields in various states that are demanded by the quantum field theory that describes our Universe. The particle-antiparticle pairs illustrated here, however, are only a calculational tool; they are not to be confused with real particles.

There’s a very common misconception about how Hawking radiation works, put forth by none other than Hawking himself in his celebrated popular book, A Brief History of Time. The way Hawking told us to envision it:

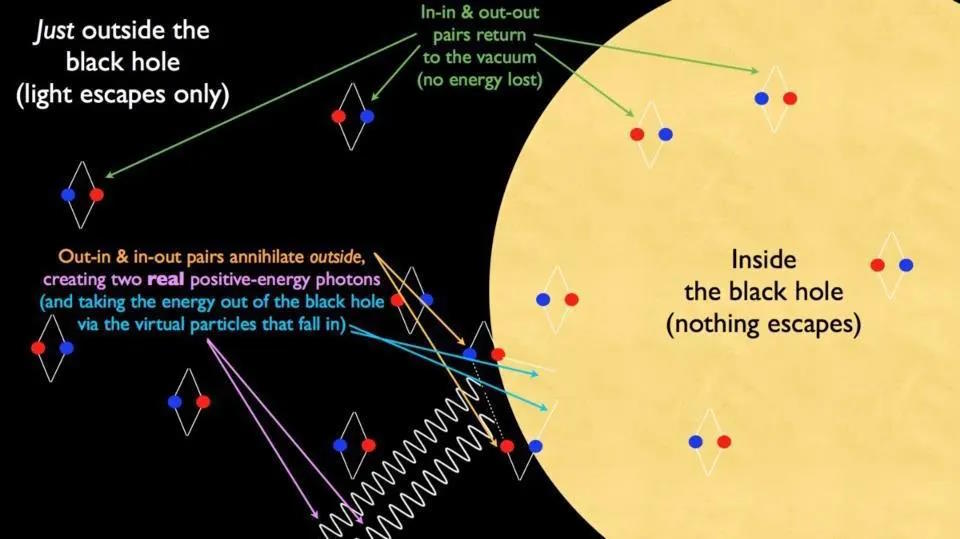
• the Universe is filled with particle-antiparticle pairs popping in-and-out of existence,
• even in empty space, as a consequence of quantum field theory and the Heisenberg uncertainty principle,
• that in uncurved space, these pairs always find one another and re-annihilate after a very small time interval,
• but if an event horizon is present, one member of the pair can “fall in” while the other “escapes,”
• leading to a situation where real particles (or antiparticles) are emitted with positive mass/energy from just outside the horizon itself,
• whereas the paired member that falls into the event horizon must have “negative energy” that subtracts from the black hole’s total mass.

It’s a convenient picture, to be sure, but it’s a picture that even Hawking himself knew must be false. Despite the fact that, in his 1974 paper, he wrote:

“It should be emphasized that these pictures of the mechanism responsible for the thermal emission and area decrease are heuristic only and should not be taken too literally,”

He does, in fact, take it literally in his 1988 book that brought this idea to the general public.

In Hawking’s most famous book, A Brief History of Time, he makes the analogy that space is filled with particle-antiparticle pairs and that one member can escape (carrying positive energy) while the other falls in (with negative energy), leading to black hole decay. This flawed analogy continues to confuse generations of physicists and laypersons alike.

The reason you cannot take this picture literally is because the particle-antiparticle pairs that pop in-and-out of existence are not actual, real particles; they are what physicists call virtual particles: a calculational tool that we use that represents fluctuations in the underlying fields, but that are not “real” in the sense that we cannot interact with or measure them directly in any way.

If you did take this picture literally, you’d erroneously think that this Hawking radiation is composed of a mixture of particles and antiparticles; it is not. Instead, it’s just composed of extremely low-energy photons in a blackbody spectrum, as even the lightest set of massive particles known, the neutrinos and antineutrinos, are far too heavy for even a single one to be produced by the real black holes in our Universe.

Instead, the actual explanation — although there are many legitimate ways to approach calculating the effect (including ways that do involve these virtual particle-antiparticle pairs) — is that it is the difference in the quantum vacuum (i.e., the fundamental properties of quantum fields in empty space) between regions of space with different amounts of spatial curvature that leads to the production of this thermal, blackbody radiation that we call Hawking radiation.

The most common, and incorrect, explanation for how Hawking radiation arises is an analogy with particle-antiparticle pairs. If one member with negative energy falls into the black hole’s event horizon, while the other member with positive energy escapes, the black hole loses mass and outgoing radiation departs the black hole. This explanation has misinformed generations of physicists and came from Hawking himself. One of the errors inherent to this explanation is the notion that all of the Hawking radiation arises from the event horizon itself: it does not.

There are a few interesting points that arise, that have been known for many decades, as a consequence of the ways Hawking radiation actually works.

Interesting point #1: The Hawking radiation itself cannot all originate from the event horizon of the black hole itself.

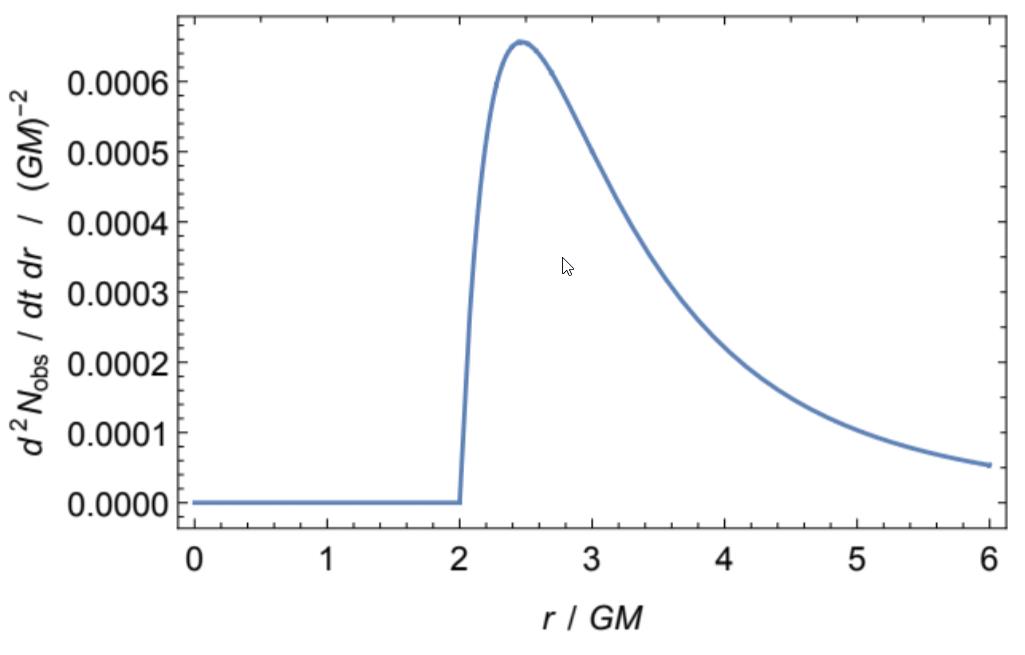
One of the fun things you can calculate, at any moment in time, is the density of the Hawking radiation that arises all throughout space. You can calculate the energy density as a function of distance from the black hole, and you can compare that to a calculation for what the expected energy density would be if the radiation all originated at the event horizon itself and then propagated outward in space.

Remarkably, those two calculations do not match up at all; in fact, most of the Hawking radiation that arises around the event horizon of the black hole originates within about 10-20 Schwarzschild radii (the radius from the singularity to the event horizon) of the event horizon, rather than at the event horizon itself. In fact, there are non-zero amounts of radiation that are emitted throughout all of space, even far away from the event horizon itself. The horizon itself may play a role that’s important in the generation of Hawking radiation, just as Unruh radiation ought to be generated owing to the presence of a cosmic horizon in our own Universe, but you cannot generate all of your Hawking radiation at the event horizon of a black hole and get predictions that are consistent with our theoretical calculations.

It must be noted that it isn’t particles or antiparticles that are produced when black holes undergo Hawking radiation, but rather photons. One can calculate this using the tools of virtual particle-antiparticle pairs in curved space in the presence of an event horizon, but those virtual pairs should not be construed as being real particles, nor should all of the radiation be construed as arising from just barely outside the event horizon.

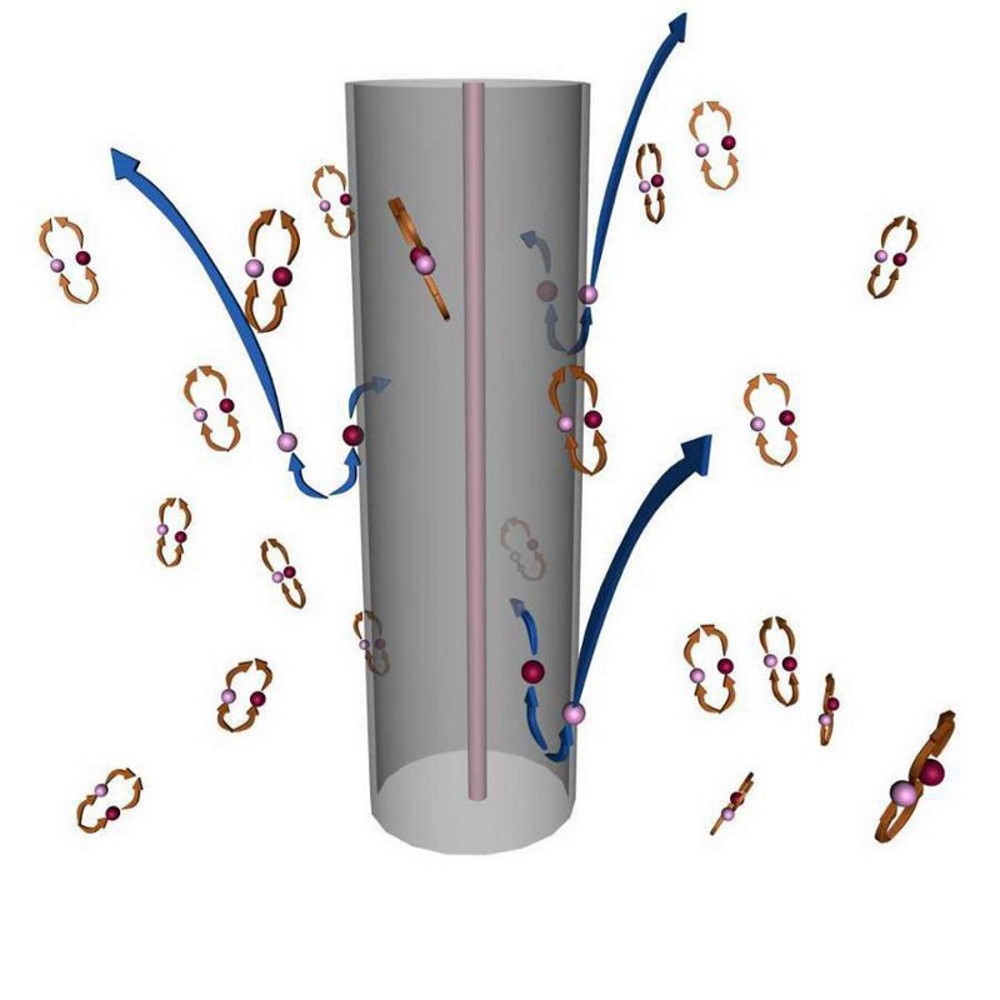
Interesting point #2: More radiation gets emitted from more severely curved regions of space, implying that lower-mass black holes emit more Hawking radiation and decay faster than higher-mass ones.

This is a point that puzzles most people the first time they hear about it: the more massive your black hole is, the less severely curved your space will be just outside the black hole’s event horizon. Yes, the event horizon is always defined by that boundary where the escape velocity of a particle is either less than the speed of light (which is outside the event horizon) or greater than the speed of light (which defines inside the event horizon), and the size of this horizon is directly proportional to the black hole’s mass.

But the curvature of space is much greater near the event horizon of a smaller, low-mass black hole than it is near the event horizon of a larger, greater-mass black hole. In fact, if we look at the properties of the emitted Hawking radiation for black holes of different (realistic) masses, we find:

• The temperature of the radiation is inversely proportional to the mass: ten times the mass means one-tenth the temperature.
• The luminosity, or radiated power, of a black hole, is inversely proportional to the square of the black hole’s mass: ten times the mass means one-hundredth the luminosity.
• And the evaporation time for a black hole, or how long it takes for a black hole to completely decay away into Hawking radiation, is directly proportional to the mass of the black hole cubed: a black hole that’s ten times as massive as another will persist for one thousand times as long.

In the far future, there will be no more matter around black holes, but instead their emitted energy will be dominated by Hawking radiation, which will cause the size of the event horizon to shrink. The transition from “growing” to “decaying” black holes will occur whenever the accretion rate drops below the mass loss rate due to Hawking radiation, an event estimated to occur some ~10^20 years in the future. How the information that went into making the black hole gets encoded into the outgoing radiation, or whether that’s even the case, has not yet been determined.

Interesting point #3: The amount by which spacetime is curved at a given distance from a mass is completely independent of how dense that mass is, or whether it has an event horizon at all.

Here’s a fun question to consider. Imagine, if you will, that the Sun was magically, instantaneously replaced with an object that was the exact same mass as the Sun but whose physical size was either:

• the size of the Sun itself (with a radius of about 700,000 km),
• the size of a white dwarf (with a radius of about 7,000 km),
• the size of a neutron star (with a radius of around 11 km),
• or the size of a black hole (whose radius would be about 3 km).

Now, imagine you’re assigned the following task: to describe what the curvature of space is, and how it’s different, between these four separate examples.

The answer, quite remarkably, is that the only differences that arise are if you’re at a location that’s inside of the Sun itself. As long as you’re more than 700,000 km away from a solar mass object, then it doesn’t matter whether that object is a star, a white dwarf, a neutron star, a black hole, or any other object with or without an event horizon: its spacetime curvature and properties are the same.

Although the amount that spacetime is curved and distorted depends on how dense the object in question is when you’re close to the object’s edge, the size and volume that the object occupies is unimportant far away from the mass itself. For a black hole, neutron star, white dwarf, or a star like our Sun, the spatial curvature is identical at sufficiently large radii. However, close to the event horizon of a black hole, more severe curvatures are achieved than anywhere else. Far away from all of these sources, spacetime is asymptotically flat, but neither perfectly flat nor truly empty.

If you put these three points together, you might start wondering for yourself what many physicists have wondered for a very long time: does Hawking radiation only occur around black holes, or does it occur for all massive objects within spacetime?

Although the event horizon was a key feature in Hawking’s original derivation of the radiation that now bears his name, there have been other derivations (sometimes in alternate numbers of dimensions) that have shown this radiation still exists in curved spacetime, irrespective of the presence or absence of such a horizon.

That’s where the new paper that comes in is so interesting: the only role the event horizon plays is to serve as a boundary for where radiation can be “captured” from versus where it can “escape” from. The calculation is done in fully four-dimensional spacetime (with three space and one time dimension), and shares many important features with other approaches to calculating the presence and properties of Hawking radiation. The boundary for what gets captured versus what escapes would still exist for any other example of a mass we chose:

• it would be the event horizon for a black hole,
• the surface of a neutron star for a neutron star,
• the outermost layer of a white dwarf for a white dwarf,
• or the photosphere of a star for a star.

In all cases, there would still be an escape fraction that depended on the mass and radius of the object in question; there’s nothing special about the presence or absence of an event horizon.

The event horizon of a black hole has been considered an important factor in the generation of Hawking radiation around black holes in many previous studies, but a new one suggests that this radiation can still be generated outside of an event horizon even if the horizon itself does nothing more than forbid light from escaping from within it.

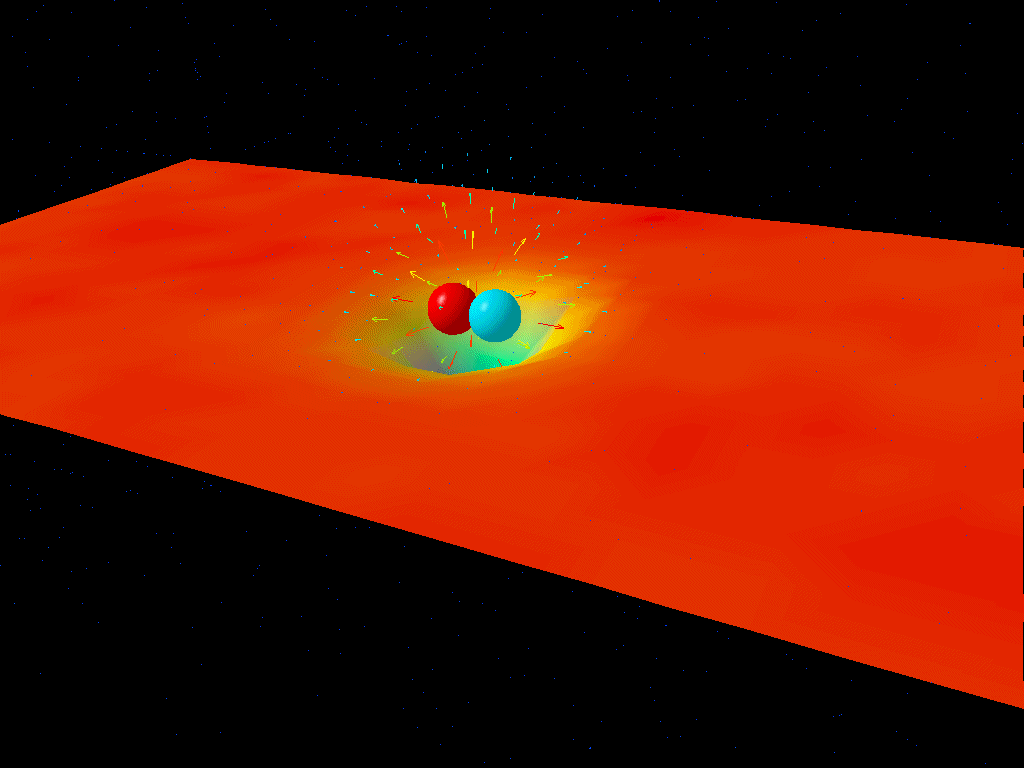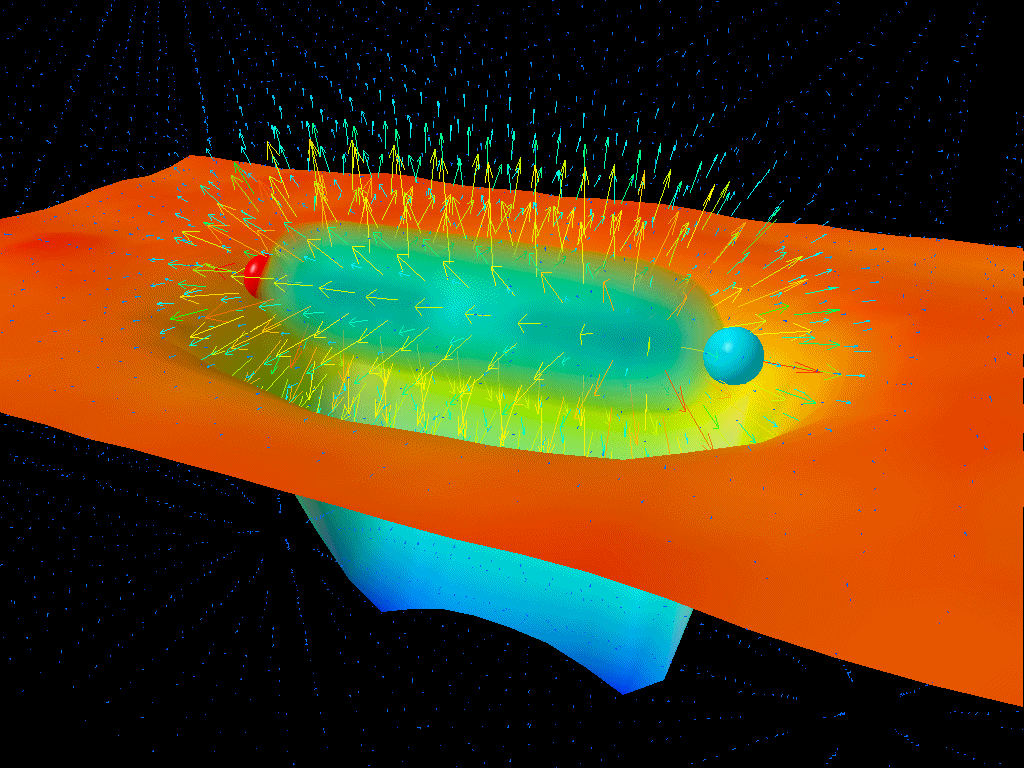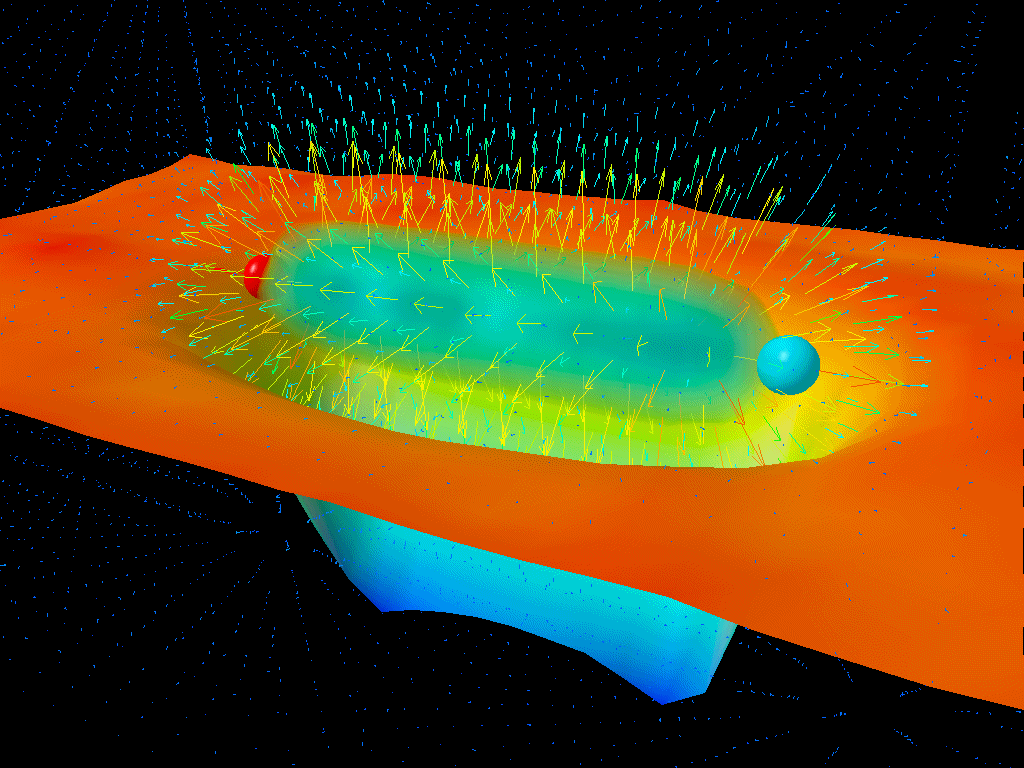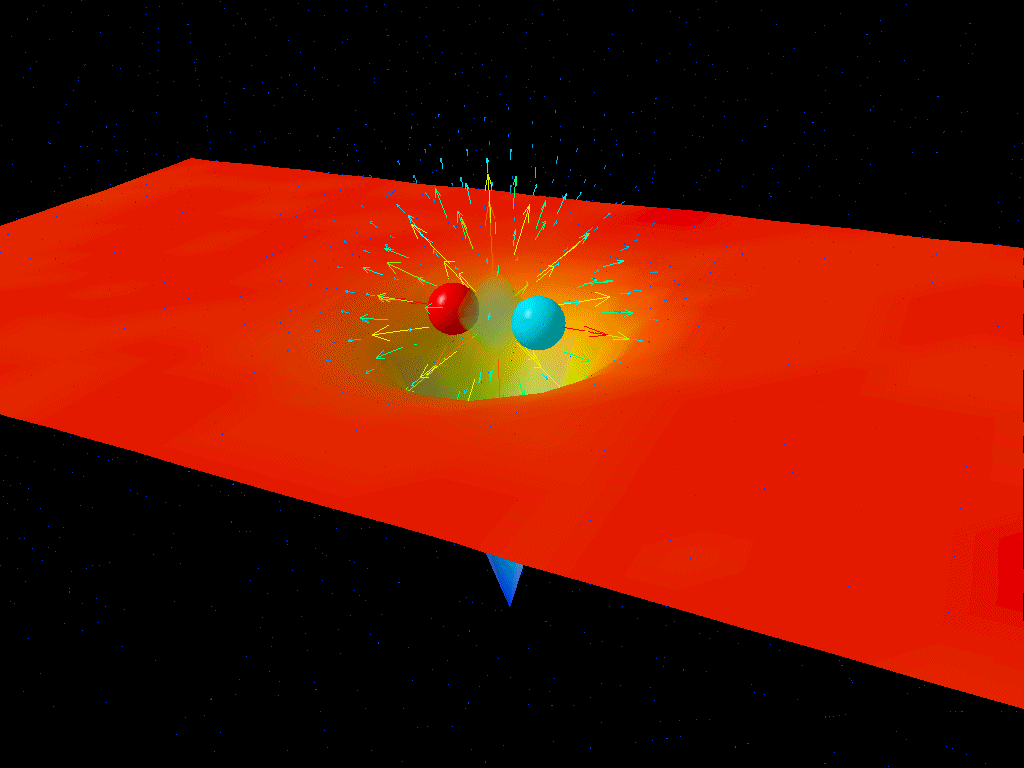
There’s a very simple analogy to the approach that Wondrak, van Suijlekom, and Falcke take in their paper: to that of the Schwinger effect in electromagnetism. Way back in 1951, physicist Julian Schwinger — one of the co-discoverers of quantum electrodynamics — detailed how matter could be created from pure energy in the vacuum of space simply by creating a strong enough electric field. Whereas you can envision quantum field fluctuations however you like in the absence of an external field, applying a strong external field polarizes even the vacuum of space: separating positive from negative charges. If the field is strong enough, these virtual particles can become real, stealing energy from the underlying field to keep energy conserved.

Instead of an electric field, charged particles, and the Schwinger effect, the gravitational analogue is simply to use the background of curved spacetime for the electric field, to substitute an uncharged, massless scalar field for the charged particles: a simplistic analogue to stand-in for the photons that would be produced via Hawking radiation. Instead of the Schwinger effect, what they see is the production of new quanta in this curved spacetime, with a “production profile” that depends on the radius you are away from the event horizon. But note that there’s nothing special about the horizon itself: production occurs at all distances sufficiently far from the object itself.

As calculated in an interesting and suggestive 2023 paper, there is no emitted radiation from inside a black hole’s event horizon (less than “2” on the x-axis), but the radiation arises from an infinitely-extending region outside of the event horizon, peaking at 25% larger than the horizon itself but falling off slowly thereafter. The implication is that even massive objects without an event horizon, like stars, may emit some amount of Hawking radiation.

The key takeaway, assuming the paper’s analysis is valid (which of course requires independent confirmation), is that there is no “special role” played by the event horizon as far as the production of radiation (or any other types of particles) goes. Quite generally, if you have

• a quantum field theory,
• with creation and annihilation operators,
• with some sort of tidal, differential forces acting on the field fluctuations (or virtual particles and antiparticles, if you prefer),
• that will create an additional separative effect over what you’d expect in a uniform background of empty space,

then you can conclude that a fraction of the particles that are produced will escape, in a radius-dependent fashion, irrespective of the presence or absence of an event horizon.

It’s perhaps important to note that this new work does not reproduce all of the known features of Hawking radiation exactly; it is only a simplistic model that stands in for a realistic black hole. Nevertheless, many of the lessons gleaned from this study, as well as from the toy model motivating it, may prove to be incredibly important for understanding not only how Hawking radiation works, but under what circumstances and conditions it gets generated by. It also sets the stage, just as has been already accomplished for the Schwinger effect, for condensed matter analogue systems to be constructed, where this effect may actually be quantifiable and observable.

In theory, the Schwinger effect states that in the presence of strong enough electric fields, (charged) particles and their antiparticle counterparts will be ripped from the quantum vacuum, empty space itself, to become real. Theorized by Julian Schwinger in 1951, the predictions were validated in a tabletop experiment, using a quantum analogue system, for the first time. Although this shows how something can arise from empty space, it’s irresponsible to equate “empty space” with the philosophical concept of “nothingness.”

One of the things I greatly appreciate about this paper is that it corrects a big, widespread misconception: the idea that Hawking radiation is generated at the event horizon itself. Not only is this not true, but the horizon only serves as a “cutoff point” in the sense that no radiation generated inside of it can escape. Instead, there is a specific radial production profile for this radiation, where there’s a peak amount of radiation that is generated and escapes at about 125% of the event horizon’s radius, and then that radiation falls off and asymptotes to zero at greater radii, but there’s always some non-zero amount of production that can be predicted.

An interesting thing to think about is that, for black holes, there is no external energy reservoir to “draw” this energy from, and hence the energy for this radiation must come from the massive object at the center, itself. For a black hole, that means it must decay, leading to its eventual evaporation.

The event horizon of a black hole is a spherical or spheroidal region from which nothing, not even light, can escape. But outside the event horizon, the black hole is predicted to emit radiation. Hawking’s 1974 work was the first to demonstrate this, and it was arguably his greatest scientific achievement. Although this treatment isn’t dependent on whether spacetime and gravity are quantum or not, treating gravity semiclassically has pathological consequences under a variety of circumstances.

But for objects that aren’t black holes, what is it, specifically, that will occur? Will this emitted radiation steal energy from the self-gravitational energy of an object like a star or stellar remnant, leading to gravitational contraction? Will it eventually lead to particle decays, or even some sort of phase transition within this object? Or does it imply something far more profound: such as once certain limits are reached and surpassed, that all matter will eventually collapse to a black hole and, via Hawking radiation, eventually decay?

At this point, these are just speculations, as they’re questions that can only be answered by follow-up work. Nevertheless, this paper is a clever line of thought, and does something remarkable: it poses and analyzes a nearly 50-year-old problem in an entirely new way. Perhaps, if nature is kind, this will wind up bringing us closer to resolving some of the key, core issues at the very hearts of black holes. Although it’s still just a suggestion, the implication is certainly worth considering: that all masses, not just black holes, may wind up emitting Hawking radiation.