Ask Ethan: How many constants define our Universe?

- Some aspects of our Universe, like the strength of gravity’s pull, the speed of light, and the mass of an electron, don’t have any underlying explanation for why they have the values they do.
- For each aspect like this, a fundamental constant is required to “lock in” the specific value that we observe these properties take on in our Universe.
- All told, we need 26 fundamental constants to explain the known Universe: the Standard Model plus gravity. But even with that, some mysteries still remain unsolved.
Although it’s taken centuries of science for us to get there, we’ve finally learned, at an elementary level, what it is that makes up our Universe. The known particles of the Standard Model comprise all of the normal matter that we know of, and there are four fundamental interactions that they experience: the strong and weak nuclear forces, the electromagnetic force, and the force of gravity. When we place those particles down atop the fabric of spacetime, the fabric distorts and evolves according to the energy of those particles and the laws of Einstein’s General Relativity, while the quantum fields they generate permeate all of space.
But how strong are those interactions, and what are the elementary properties of each of those known particles? Our rules and equations, as powerful as they are, don’t tell us all of the information we require to know those answers. We need an additional parameter to answer many of those questions: a parameter that we must simply measure to know what it is. Each such parameter translates to a needed fundamental constant in order to completely describe our Universe. But how many fundamental constants does that equate to, today? That’s what Patreon supporter Steve Guderian wants to know, asking:
“What is the definition of a [fundamental] physical constant, and how many are there now?”
It’s a challenging question without a definitive answer, because even the best description we can give of the Universe is both incomplete and also may not be the most simple. Here’s what you should think about.
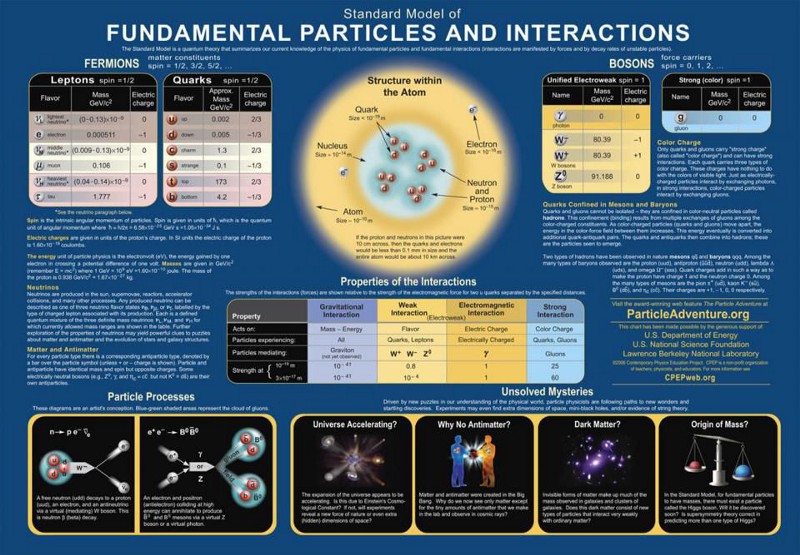
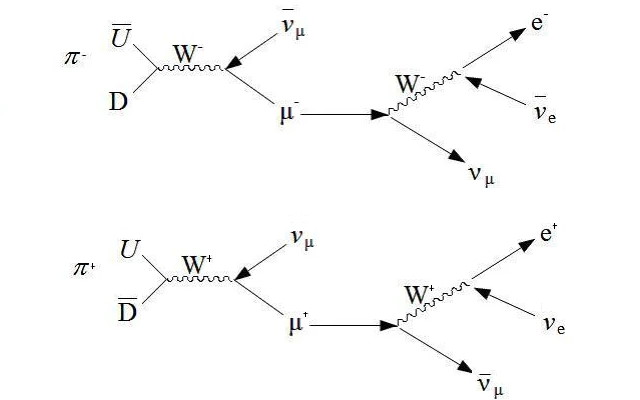
Think about any particle at all, and how it might interact with another. One of the simplest fundamental particles is an electron: the lightest charged, point-like particle. If it encounters another electron, it’s going to interact with it in a variety of ways, and by exploring its possible interactions, we can understand the notion of where you need a “fundamental constant” to explain some of those properties. Electrons, for example, have a fundamental charge associated with them, e, and a fundamental mass, m.
- These electrons will gravitationally attract one another proportional to the strength of the gravitational force between them, which is governed by the universal gravitational constant: G.
- These electrons will also repel one another electromagnetically, inversely proportional to the strength of the permittivity of free space, ε.
There are other constants that play a major role in how these particles behave as well. If you want to know how fast an electron moves through spacetime, it has a fundamental limit: the speed of light, c. If you force a quantum interaction to occur, say, between an electron and a photon, you’ll encounter the fundamental constant associated with quantum transitions: Planck’s constant, ħ. There are weak nuclear interactions that the electron can take part in, such as nuclear electron capture, that require an additional constant to explain their interaction strength. And although the electron doesn’t engage in them, there’s also the possibility of a strong nuclear action between a different set of particles: the quarks and gluons.
However, all of these constants have units attached to them: they can be measured in units like Coulombs, kilograms, meters-per-second, or other quantifiable physical quantities. These units are arbitrary, and an artifact of how, as humans, we measure and interpret them.
When physicists talk about truly fundamental constants, they recognize that there’s no inherent importance to ideas like “the length of a meter” or the “time interval of a second” or “the mass of a kilogram” or any other value. We could work in any units we liked, and the laws of physics would behave exactly the same. In fact, we can frame everything we’d ever want to know about the Universe without defining a fundamental unit of “mass” or “time” or “distance” at all. We could describe the laws of nature, entirely, by using solely constants that are dimensionless.
Dimensionless is a simple concept: it means a constant that’s just a pure number, without meters, kilograms, seconds or any other “dimensions” in them. If we go that route to describe the Universe, and get the fundamental laws and initial conditions correct, we should naturally get out all the measurable properties we can imagine. This includes things like particle masses, interaction strengths, cosmic speed limits, and even the fundamental properties of spacetime. We would simply define their properties in terms of those dimensionless constants.

You might wonder, then, how you could describe things like a “mass” or an “electric charge” with a dimensionless constant. The answer lies in the structure of our theories of matter and how it behaves: the theories of our four fundamental interactions. Those interactions, also known as the fundamental forces, are:
- the strong nuclear force,
- the weak nuclear force,
- the electromagnetic force,
- and the gravitational force,
all of which can be recast in either quantum field theoretic (i.e., particles and their quantum interactions) or General Relativistic (i.e., the curvature of spacetime) formats.
You might look at the particles of the Standard Model and think, “Oh geez, look at their electric charges. Some have a charge that’s the electron’s charge (like the electron, muon, tau, and W- boson), some have a charge that’s ⅓ of the electron’s charge (the down, strange, and bottom quarks), some have a charge that’s -⅔ of the electron’s charge (the up, charm, and top quarks), and others are neutral. And then, on top of that, the antiparticles all have the opposite charge of the ‘particle version.'”
But that doesn’t mean each one needs their own constant; the structure of the Standard Model (and specifically, of the electromagnetic force within the Standard Model) gives you the charges of each particle in terms of one another. As long as you have the structure of the Standard Model, just one constant — the electromagnetic coupling of particles within the Standard Model — is sufficient to describe the electric charges of every known particle.
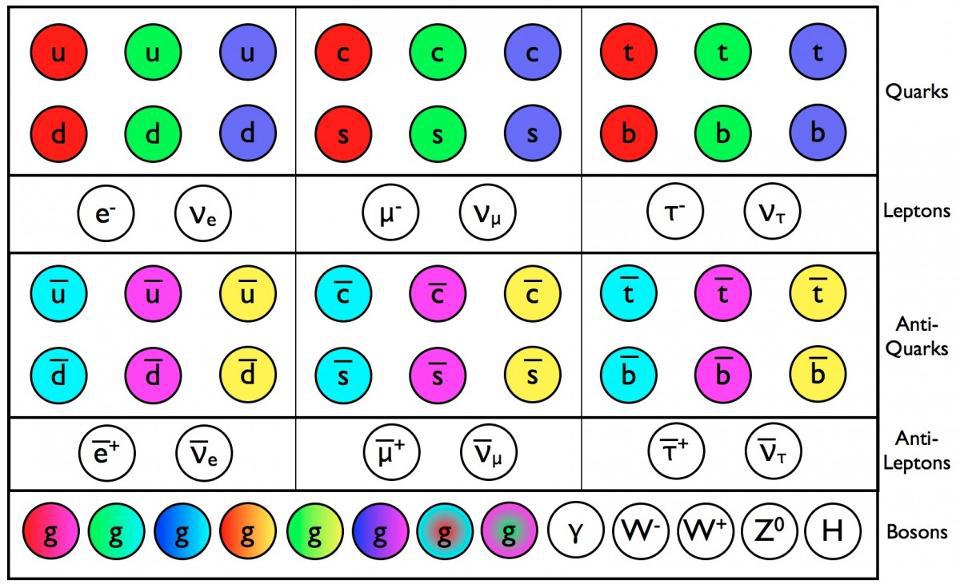
Unfortunately, the Standard Model — even the Standard Model plus General Relativity — doesn’t allow us to simplify every descriptive parameter in this fashion. “Mass” is a notoriously difficult one: one where we don’t have a mechanism to interrelate the various particle masses to one another. The Standard Model can’t do it; each massive particle needs its own unique (Yukawa) coupling to the Higgs, and that unique coupling is what enables particles to get a non-zero rest mass. Even in String Theory, a purported way to construct a “theory of everything” that successfully describes every particle, force, and interaction in the framework of one overarching theory, can’t do that; Yukawa couplings simply get replaced by “vacuum expectation values,” which again are not derivable. One must measure these parameters in order to understand them.
With that said, here is a breakdown of how many dimensionless constants are needed to describe the Universe to the best of our understanding, including:
- what those constants give us,
- what possibilities there are to reduce the number of constants to get the same amount of information out,
- and what puzzles remain unanswered within our present framework, even given those constants.
It’s a sobering reminder of both how far we’ve come, as well as how far we still need to go, in order to have a full comprehension of all that’s in the Universe.
1.) The fine-structure constant (α), or the strength of the electromagnetic interaction. In terms of some of the physical constants we’re more familiar with, this is a ratio of the elementary charge (of, say, an electron) squared to Planck’s constant and the speed of light. That combination of constants, together, gives us a dimensionless number that’s calculable today! At the energies currently present in our Universe, this number comes out to ≈ 1/137.036, although the strength of this interaction increases as the energy of the interacting particles rise. In combination with a few of the other constants, this allows us to derive the electric charge of each elementary particle, as well as their particle couplings to the photon.
2.) The strong coupling constant, which defines the strength of the force that holds individual baryons (like protons and neutrons) together, as well as the residual force that allows them to bind together in complex combinations of atomic nuclei. Although the way the strong force works is very different from the electromagnetic force or gravity — getting very weak as two (color-charged) particles get arbitrarily close together but stronger as they move apart — the strength of this interaction can still be parametrized by a single coupling constant. This constant of our Universe, too, like the electromagnetic one, changes strength with energy.
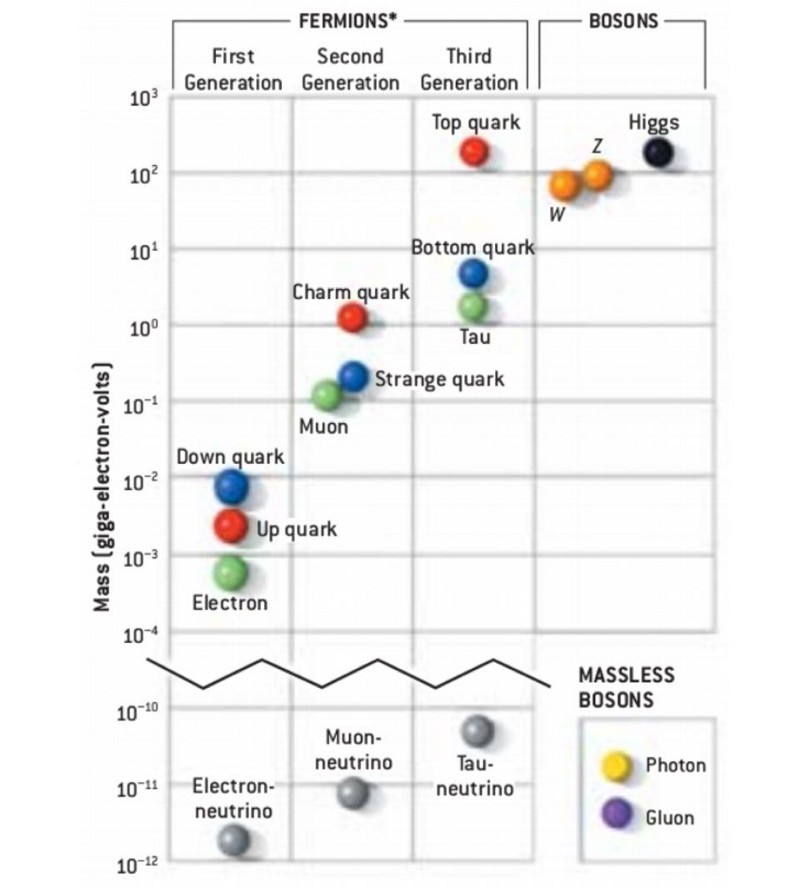
3.) through 17.) The 15 couplings to the Higgs of the 15 Standard Model particles with non-zero rest masses. Each of the six quarks (up, down, strange, charm, bottom, and top), all six of the leptons (including the charged electron, muon, and tau plus the three neutral neutrinos), the W-boson, the Z-boson, and the Higgs boson, all have a positive, non-zero rest mass to them. For each of these particles, a coupling — including, for the Higgs, a self-coupling — is required to account for the values of mass that each of the massive Standard Model particles possess.
It’s great on one hand, because we don’t need a separate constant to account for the strength of gravitation; it gets rolled into this coupling.
But it’s also disappointing. Many have hoped that there would be a relationship we could find between the various particle masses. One such attempt, the Koide formula, looked like a promising avenue in the 1980s, but the hoped-for relations turned out only to be approximate. In detail, the predictions of the formula fell apart.
Similarly, colliding electrons with positrons at a specific energy — half the rest-mass energy of the Z-boson apiece — will create a Z-boson. Colliding an electron at that same energy with a positron at rest will make a muon-antimuon pair at rest, a curious coincidence. Only, this too is just approximately true; the actual muon-antimuon energy required is about 3% less than the energy needed to make a Z-boson. These tiny differences are important, and indicate that we do not know how to arrive at particle masses without a separate fundamental constant for each such massive particle.
18.) through 21.) Quark mixing parameters. There are six types of massive quark, and two pairs of three — up-charm-top and down-strange-bottom — all have the same quantum numbers as one another: same spin, same color charge, same electric charge, same weak hypercharge and weak isospin, etc. The only differences they have are their different masses, and the different “generation number” that they fall into.
The fact that they have the same quantum numbers allow them to mix together, and a set of four parameters, parameters from what’s known as the CKM mixing matrix (after three physicists, Cabibbo, Kobayashi, and Maskawa) are required to describe specifically how they mix, enabling them to oscillate into one another.
This is a vital process essential to the weak interaction, and it shows up in measuring how:
- more massive quarks decay into less massive ones,
- how CP-violation occurs in the weak interactions,
- and how radioactive decay works in general.
The six quarks, all together, require three mixing angles and one CP-violating complex phase to describe, and those four parameters are an additional four fundamental, dimensionless constants that we cannot derive, but must be measured experimentally.

22.) through 25.) The neutrino mixing parameters. Similar to the quark sector, there are four parameters that detail how neutrinos mix with one another, given that the three types of neutrino species all have the same quantum number. Although physicists initially hoped that neutrinos would be massless and not require additional constants (they’re now part of the 15, not 12, constants needed to describe the masses of Standard Model particles), nature had other plans. The solar neutrino problem — where only a third of the neutrinos emitted by the Sun were arriving here on Earth — was one of the 20th century’s biggest conundrums.
It was only solved when we realized that neutrinos:
- had very small but non-zero masses,
- mixed together,
- and oscillated from one type into another.
The quark mixing is described by three angles and one CP-violating complex phase, and the neutrino mixing is described in the same way, with this specific PMNS matrix having a different name after the four physicists who discovered and developed it (Pontecorvo–Maki–Nakagawa–Sakata matrix) and with values that are completely independent of the quark mixing parameters. While all four parameters have been experimentally determined for the quarks, the neutrino mixing angles have now been measured, but the CP-violating phase for the neutrinos has still only been extremely poorly determined as of 2023.
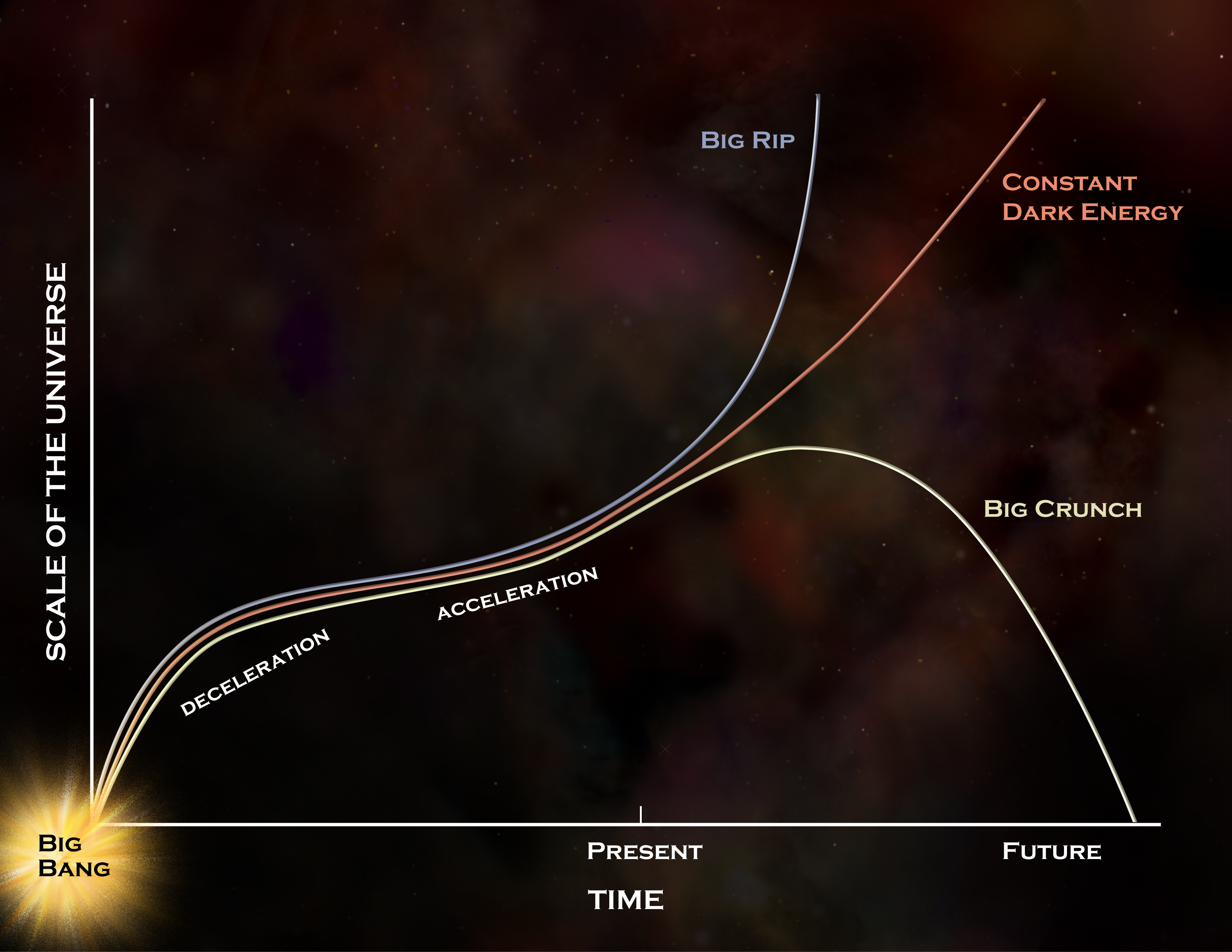
26.) The cosmological constant. The fact that we live in a dark-energy rich Universe requires at least one additional fundamental parameter over and above the ones we’ve listed already, and the simplest parameter is a constant: Einstein’s cosmological constant. This was not expected to be there, but it must be accounted for, and there’s no way to do that without adding an additional parameter within our current understanding of physics.
Even with this, there are still at least four additional puzzles that may yet mandate we add even more fundamental constants to fully explain. These include:
- The problem of the matter-antimatter asymmetry, also known as baryogenesis. Why is our Universe predominantly made up of matter and not antimatter, when the interactions we know of always conserve the number of baryons (versus antibaryons) and leptons (versus antileptons)? This likely requires new physics, and possibly new constants, to explain.
- The problem of cosmic inflation, or the phase of the Universe that preceded and set up the hot Big Bang. How did inflation occur, and what properties did it have in order to enable our Universe to emerge as it has? Likely at least one, and potentially more, new parameters will be needed.
- The problem of dark matter. Is it made of a particle? If so, what are that particle’s properties and couplings? If it’s made of more than one type of particle (or field), there is likely going to be more than one new fundamental constant required to describe them.
- The problem of why there’s only CP-violation in the weak interactions, and not the strong ones. We have a principle in physics — the totalitarian principle — that states, “Anything not forbidden is compulsory.” In the Standard Model, nothing forbids CP-violation in either the weak or strong nuclear interactions, but we only observe it in the weak interactions. If it shows up in the strong interactions, we need an additional parameter to describe it; if it doesn’t, we likely need an additional parameter to restrict it.

If you give a physicist the laws of physics, the initial conditions of the Universe, and the aforementioned 26 constants, they can successfully simulate and calculate predictions for any aspect of the Universe you like, to the limits of the probabilistic nature of outcomes. The exceptions are few but important: we still can’t explain why there’s more matter than antimatter in the Universe, how the hot Big Bang was set up by cosmic inflation, why dark matter exists or what its properties are, and why there is no CP-violation in the strong interactions. It’s an incredibly successful set of discoveries that we’ve made, but our understanding of the cosmos remains incomplete.
What will the future hold? Will a future, better theory wind up reducing the number of fundamental constants we need, like the Koide formula dreams of doing? Or will we wind up discovering more phenomena (like massive neutrinos, dark matter, and dark energy) that require us to add still greater numbers of parameters to our Universe?
The question is one we cannot answer today, but one that’s important to continue to ask. After all, we have our own ideas about what “elegant” and “beautiful” are when it comes to physics, but whether the Universe is fundamentally simple or complex is something that physics cannot answer today. It takes 26 constants to describe the Universe as we know it presently, but even that large number of free parameters, or fundamental constants, cannot fully explain all there is.
Send in your Ask Ethan questions to startswithabang at gmail dot com!