Ask Ethan: Do infinite copies of me exist in the Multiverse?

- The observable Universe, with all the stars, planets, creatures, and particles within it, although enormous, is still finite in both size and age.
- With more “universe” certainly out there beyond what we can observe, many wonder if it’s truly an infinite cosmos that we inhabit.
- But there are also an infinite set of quantum possibilities that can occur. Are there an infinite number of “copies” of you out there in a parallel Universe? The answer depends on which infinity is bigger.
When we look out into the Universe, we find that even if we restrict ourselves to what we can observe, the Universe itself is absolutely tremendous. There are trillions upon trillions of galaxies present within it, strewn across several tens of billions of light-years in space. Further out there, beyond the observable limits of our cosmic horizon, is certainly more Universe: with more galaxies, more stars, and more planets, perhaps even an infinite number of them all told. But there are also a very large, perhaps even infinite, number of possible quantum outcomes that can occur within the Universe. Could there be enough galaxies, stars, and “copies” of what we know of to contain all of these quantum possibilities?
One of the most surprising mathematical facts that people learn is that the concept of infinity — that no matter how high you count, or how large you imagine a number to be, it’s always infinitely far away from “infinity” — is that not all infinities are the same. Some types of infinity truly are larger than others: like they’re somehow a greater degree of “infinite” than other infinities. It was this line of thought that led Daniel Krstyen to write in and ask:
“I learned that some infinities are bigger than others. What does this imply for how many “copies” of me there can be in a parallel universe scenario?”
Let’s start with infinity, and work our way up to the Multiverse, and the notion of infinite parallel universes, from there.

Most people first learn about the concept of infinity simply by counting upward — 1, 2, 3, 4, 5, etc. — and recognizing that no matter how large a number they reach, into the thousands, millions, billions, trillions, or beyond, there’s simply no limit to how high you can go. “Forever” seems to be the answer, meaning that you can never reach the end when it comes to how high you can count. In other words, you can count as high as you like, for as long as you like, and you’ll never reach a point that compels you to stop. You can count arbitrarily high, approaching, but never reaching, the concept of infinity as you go higher and higher.
But what if you changed the way you counted? Instead of:
- 1, 2, 3, 4, 5, …
what if you started at 0, and counted both positively and negatively:
- 0, +1, -1, +2, -2, +3, -3, …
would you suddenly “double” your infinity, and have a “bigger infinity” on your hands?
What if you counted by twos instead:
- 2, 4, 6, 8, 10, …
would that be a larger infinity?
It turns out, perhaps surprisingly, that the answer is no: these are all the same infinity, what we call “countably infinite.”

As long as you can count off all of the elements in your set, even if the counting would take an infinite amount of time, you’ll be able to count off any number that’s within your set in a finite amount of time. This, believe it or not, is the smallest type of infinity that there is. And the general rule is this: if you can invent a rule that would map, 1-to-1, the natural numbers onto the set of numbers you’re considering, you have a countably infinite set of numbers.
So going up by squares — 1, 4, 9, 16, 25, etc. — is a countably infinite set of numbers.
But you know what isn’t? The set of real numbers, rationals and irrationals both, that exist between 0 and 1.
The way to see this is as follows: take your sequence of natural numbers — 1, 2, 3, 4, 5, etc. — and take their reciprocals. What do you get? You get a series that goes like this:
- 1, ½, ⅓, ¼, ⅕, ⅙, ⅐, ⅛, etc.
Notice how, no matter how high you count, you always get a number larger than 0, but still smaller than 1. In other words, there are an infinite number of numbers between 0 and 1, and still, that doesn’t include them all. Everything between ½ and 1, for example, isn’t included. Irrational numbers, like 1/e, π/4, or √½, also aren’t included. The set of real numbers between 0 and 1 is an example of a second type of “infinite number,” which is known as an uncountable infinity.

There are mathematically rigorous ways to compare different sets of numbers and see “which infinity is bigger,” and that’s the type of exercise we’re going to have to engage in if we want to know if there are copies of you out there, somewhere, in the Multiverse or not. After all, we have two things we need to compare to one another, and both are incredibly large sets of information. One of them is “How many universes are there out there in the entire, unobservable universe?” and the other is “How many possible quantum outcomes are there that could have occurred, since the start of the hot Big Bang, within our Universe?”
If we can imagine a large enough set of actual universes that start off identically (or, at least, similarly enough) to our own, we can imagine that as time begins passing and each universe expands, cools, and has the particles (and antiparticles) within it interact, there are going to be a large number of possible quantum outcomes that can occur. This number should increase as time goes on: it should increase very rapidly, as each new quantum interaction that occurs will have a set of possible outcomes, and then each one of those “new” outcomes leads to its own set of new possibilities, and so on, and so on, etc.

As long as there’s a finite amount of time that’s passed and a finite number of particles and interactions that occur within each universe, there’s going to be a finite theoretical number of “identical universes” we’d need to start off with to contain all of the possible quantum outcomes that could have occurred by now.
- If the actual number of identical universes is greater than that number, then there are plenty of copies of you, including copies that made one (or more) critical, life-affecting decisions differently from your own choices. That means, somewhere out there, there’s probably a “you” that has a better, happier life than you have, and somewhere else, a version of “you” that has it far worse.
- If the actual number of identical universes is less than that number, then you’re almost certainly the only “you” out there, and as time goes on, the different universes that exist will rapidly diverge from one another: no two will be even alike, much less identical.
- And, finally, if the actual number of identical universes is equal to that number, then there’s probably only one exact “you” out there in the multiverse, and it’s the one that’s right here, right now. But others will be very close to ours: with only a handful of quantum outcomes that occurred differently. As time goes on, the one that grows faster — either the “number of identical universes” or the “number of possible outcomes” — will determine whether more copies of you arise or more possible outcomes arise.
This is exciting, because we can estimate all sorts of properties about the observable Universe, including its age, the number of particles within it, how frequently these particles interact with one another, and what types of quantum outcomes are possible. From that, we can actually estimate how many parallel universes we’d actually need there to be within the multiverse to account for each possible outcome.
We can also estimate how much volume there is to the entire universe, including the unobservable part that goes well beyond what we can see or gain information about, based on the best theory of our cosmic origins: cosmic inflation, which occurred prior to and set up the conditions for the hot Big Bang.
You might object to this line of thought, because it’s possible that either:
- the universe could be truly infinite, going on forever and ever in extent, and so there are a truly infinite set of “identical-to-our-own-observable-universe” universes out there,
- or that cosmic inflation occurred for a truly infinite amount of time, and has been creating “new universes” forever, meaning that there are an infinite set of universes out there, whereas there are only a finite set of possible quantum outcomes.
The first objection is valid: we don’t know if the true size of the unobservable universe is infinite or not; it could be, as there’s nothing that forbids it from being so. But the second objection isn’t valid, and thinking about why tells us how we should approach this problem.
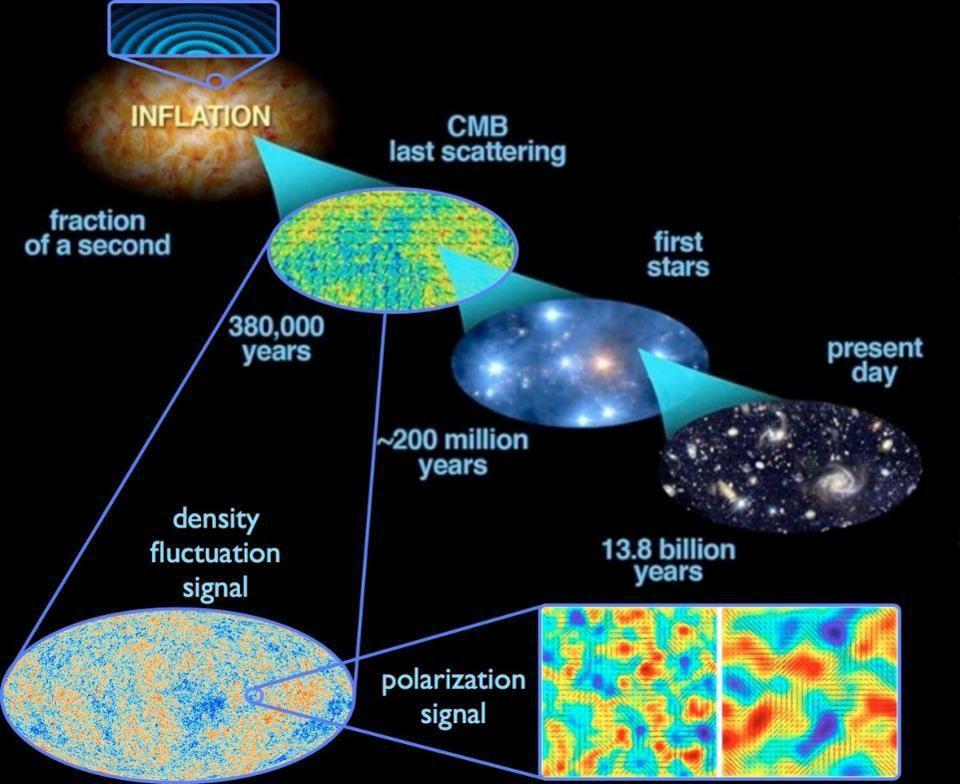
According to the theory of cosmic inflation, prior to the hot Big Bang, the universe was expanding at a relentless, exponential rate, doubling in size (in each of our three dimensions) with each tiny fraction-of-a-second, something like ~10-35 seconds, that goes by. As time goes by in this inflationary phase, the volume of space grows remarkably quickly.
- After 10-35 seconds (1 doubling), space is 8 (23) times its original volume.
- After 10-34 seconds (10 doublings), space is 1,073,741,824 (230) times its original volume.
- After 10-33 seconds (100 doublings), space is 2.037 × 1090 (2300) times its original volume.
In other words, the volume of space, during this inflationary period, does indeed grow toward infinity, and does so at an exponential rate.
This is faster than the rate at which any of the “countable infinities” that we can concoct grows at. After one second of inflation, the volume of space would be 2300000000000000000000000000000000000 its original volume, showcasing just how fast an inflationary universe grows.
Moreover, once inflation begins in one region of space, it’s very difficult to get it to cease altogether. In fact, as long as inflation is an inherently quantum process, then for every region of space where inflation does come to an end, triggering a hot Big Bang (and a universe like our own), it will be surrounded by regions where inflation continues. This creates a multiverse, where different regions where hot Big Bangs occur are separated by more inflating space, which drive these regions apart and ensure that no two “baby universes” ever collide or interact with one another.

However, the very same laws of physics that point to inflation being “eternal” in this fashion — where once it gets started, it’s always going to continue somewhere — point to the impossibility of it being eternal to the past. Although we cannot state for certain what came before inflation, we can be fairly certain (although some loopholes are proving stubbornly difficult to close) that its duration hasn’t been truly infinite, at least so far. Inflation may have lasted a fraction of a second, several seconds, or even for billions upon billions of years (or longer), but it could not have been occurring for a truly infinite amount of time.
On the other hand, since the start of the hot Big Bang, each subatomic particle that exists — somewhere around 1090 of them if you include photons, neutrinos, and all of the subatomic particles that make up atoms — experiences trillions upon trillions of interactions with other quantum particles in the Universe merely during the first second after the Big Bang. The order of each collision and interaction matters; the types of particle-antiparticle pairs that are randomly produced by energetic enough interactions matter; the random angles at which energy-and-momentum conserving processes send particles off in matter; etc.

Whenever you have a system of a large number of particles that all interact, the number of possible combinations for the outcome of those interactions grows extremely rapidly. Not linearly, not as a power law, and not even exponentially, but faster than all of those: according to the science of combinatorics.
The mathematics of combinatorics looks a lot like the mathematics of permutations: a.k.a., factorials. If you have 5 different particles and ask, “How many ways are there to order these particles?” the answer is 5!, where the “!” symbol stands for factorial, and where 5! = 5 × 4 × 3 × 2 × 1, for a total of 120 possible permutations in this example.
And this is where the resolution to our problem becomes apparent. With 1090 quanta in the Universe that are capable of interacting, and with an enormous number of these quanta bound together in systems like planets, stars, and galaxies, they interact over and over again throughout time. The number of quantum possibilities grows in this fashion — combinatorically, or like a factorial — which grows far more quickly than any other type of growth we’ve looked at so far. You can see this by comparing linear growth (~x) with power law growth (~x2) with exponential growth (~2x) with combinatoric growth (~x!) as follows:
- linear: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…
- power law: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100…
- exponential: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024…
- combinatoric: 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800…
As you can see, yes, some infinities really are bigger than others, with the infinity corresponding to “the number of possible quantum outcomes” growing far, far faster than any of the others, even faster than the exponential growth of the volume of the universe that inflation predicts. This has been well-known to mathematicians for a very long time; so long that they even have a name for this phenomenon: a combinatorial explosion.
Quite simply, even with the enormous, growing, and tending-toward-infinite number of parallel universes that inflationary cosmology gives us, there still aren’t nearly enough of them to contain the quantum possibilities that exist even at the present day. Moreover, this is a problem that only worsens over time, as particles continue to interact at far greater rates than inflationary (or any other type of) expansion can keep up.
The only hope for a multiverse that contains any “copies” of you at all — much less an infinite number of them, à la Everything Everywhere All At Once — is if the universe itself were truly born infinite in some critical way: either an infinitely long time ago, with space occupying an infinite volume, or both. If we take the physical motivation for a multiverse, which comes from inflationary cosmology, the number of parallel universes it gives us is simply too small to contain all of the possible outcomes that quantum physics gives us. Some infinities truly are bigger than others, and for that reason, there’s only one “you” out there.
Send in your Ask Ethan questions to startswithabang at gmail dot com!