Why “incompleteness” matters in theoretical physics

In physics, many of our greatest advances aren’t driven merely by data that conflicts with our best theories, but rather by noticing that two disparate aspects of our best current understanding simply don’t “play nice” with one another. Paying attention to those inconsistencies often helps us realize how our current theories are, in fact, “incomplete” in a fundamental sense, and the quest to find a more complete version of them often bears a tremendous amount of fruit as far as bringing about the next step forward in our understanding of the Universe.

This has happened many times throughout history, and led to the development of a number of important advances in theoretical physics, including:

• Maxwell’s theory of electromagnetism,
• Einstein’s special relativity,
• Einstein’s general relativity,
• the Standard Model of particle physics,
• and the theory of cosmic inflation,

among many other examples. Today, many of our best theories have similar incompletenesses, and while attempts to complete them aren’t always fruitful or descriptive of reality, they suggest pathways forward that may yet lead us to a superior understanding of our physical Universe. Here’s why incompleteness is such an important concept to recognize, and how it has historically led to some of the greatest advances of all-time.

One of Faraday’s 1831 experiments demonstrating induction. The liquid battery (right) sends an electric current through the small coil (A). When it is moved in or out of the large coil (B), its magnetic field induces a momentary voltage in the coil, which is detected by the galvanometer. As the temperature decreases, the resistance of the circuit decreases as well. In most materials, there is always a non-zero resistivity, but for some materials, below a certain temperature threshold, they become superconducting, with a resistivity of exactly zero.

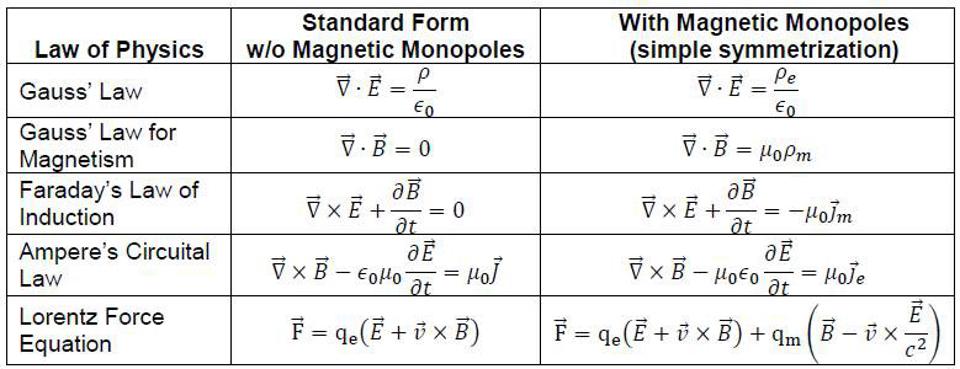
Prior to the arrival of Maxwell onto the scene, electricity and magnetism were known to be important and related phenomena. Fundamentally, there were both isolated positive and negative electric charges that created electric fields, but for magnetism, the “north” and “south” magnetic poles that created were always connected to one another, and could never exist independently; there were no isolated magnetic charges. Ampère showed that magnetic fields are related to electric current, while Faraday showed that a changing magnetic field could either be the cause of or creator of a curling (or rotating) electric field.

And it was through examining this state-of-affairs that Maxwell noticed that our understanding of electricity and magnetism was incomplete. While electricity and magnetism weren’t perfectly symmetric — as, indeed, there are no magnetic (monopole) charges — Maxwell realized that electric fields must also be allowed to vary with time. When they did, they would create a curling (or rotating) magnetic field, and conversely, if you applied a curling (or rotating) magnetic field to the right kind of system, it would cause the electric field within that system to vary as well.

Fixing the incompleteness in electricity and magnetism in this fashion led to a complete theory of classical electromagnetism, governed by Maxwell’s equations, which are still used to this day.

Light is nothing more than an electromagnetic wave, with in-phase oscillating electric and magnetic fields perpendicular to the direction of light’s propagation. The shorter the wavelength, the more energetic the photon, but the more susceptible it is to changes in the speed of light through a medium.

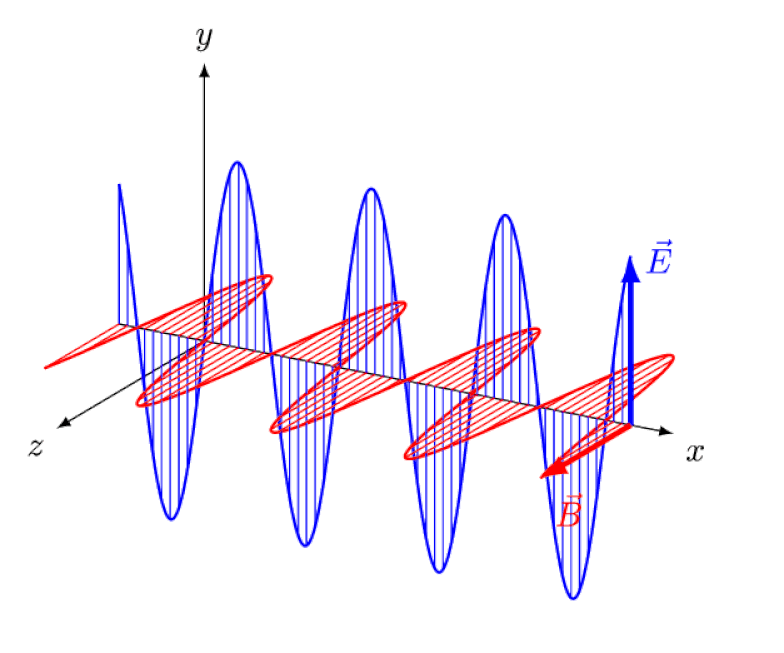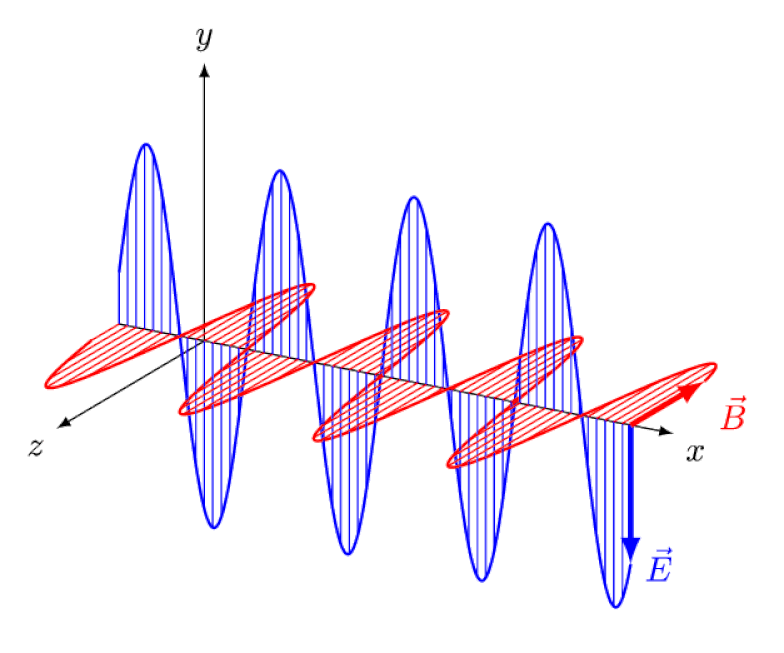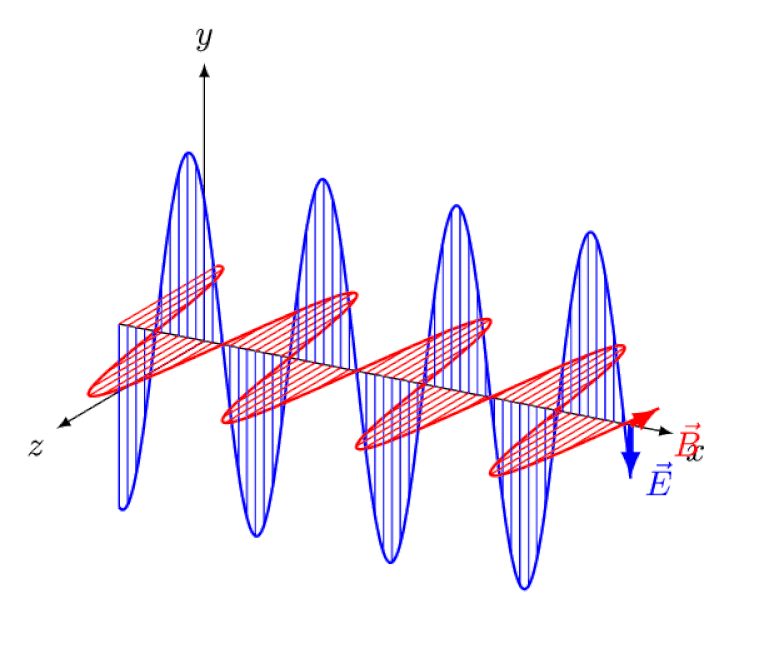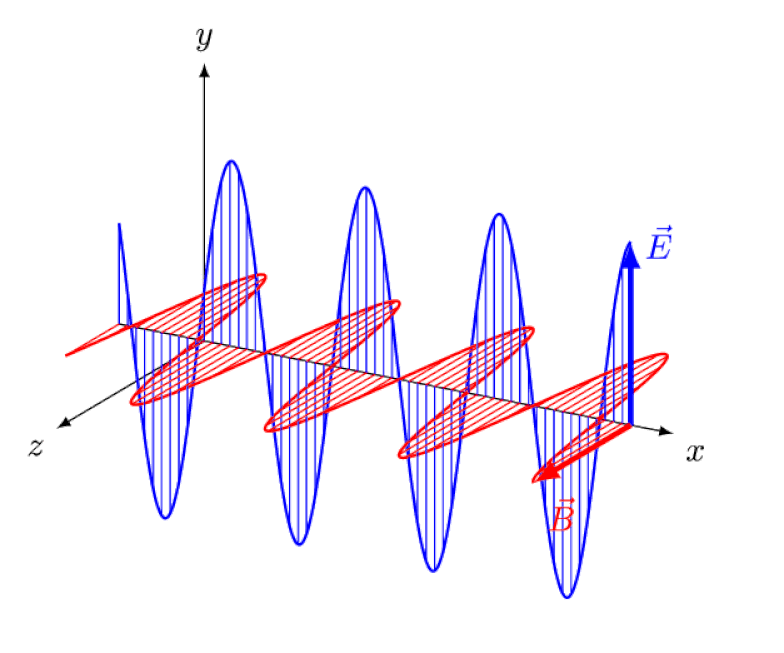
Then, in turn, Maxwell’s equations helped lead to another great advance, showing the incompleteness of Newtonian (or Galilean) motion. According to Maxwell’s theory, there should be:

• a form of electromagnetic radiation,
• that was composed of neither electric nor magnetic sources (charges),
• that always propagated at the speed of light,
• exhibiting wave-like behavior,
• and characterized by oscillating, in-phase electric and magnetic fields.

This idea, of a classical light wave, arose as a natural consequence of Maxwell’s equations, and was even derived by Maxwell himself back in the 1860s.

But this flew in the face of our prior ideas of motion, which were governed by Newtonian mechanics. No matter how quickly you moved behind a light wave, you would never observe light propagating at any other speed: only ever at the speed of light. It was exactly this line of thinking — what Einstein would later refer to as a Gedankenexperiment (or thought-experiment) — that led Einstein to the concept of special relativity and the universality of the speed of light, providing a physical basis for the previously understood concepts of length contraction and time dilation in the process.

Fixing the incompleteness between Maxwell’s theory and Newtonian mechanics was precisely what led to the birth of special relativity.

It’s possible to write down a variety of equations, like Maxwell’s equations, that describe the Universe. We can write them down in a variety of ways, but only by comparing their predictions with physical observations can we draw any conclusion about their validity. It’s why the version of Maxwell’s equations with magnetic monopoles (right) doesn’t correspond to reality, while the ones without (left) do. The displacement current term (the second term in the fourth equation) arose from Maxwell’s attempt to fix the incompleteness in electricity and magnetism that existed prior to his work.

The arrival of special relativity exposed another incompleteness: that of Newtonian gravity. (After hundreds of years of successes, the early 20th century was a very bad time for Newton!) If things like “distances” were not universal and absolute, but rather relative to the observer, then how could the force of gravity be dependent on one particular observer’s measurement of what that distance was?

It couldn’t be. Instead, Hermann Minkowski, Einstein’s former professor, created the four-dimensional concept of spacetime, and showed that there was an invariant quantity associated with it: not space nor time on its own, but a combination of the two known as a spacetime (or the Einstein) interval.

After recognizing that gravitation was just another form of acceleration, a key realization known as the equivalence principle (which Einstein would later call his “happiest thought”), Einstein set about developing a new theory of gravitation based not on the flat spacetime of Minkowski, but a curved spacetime instead. Eventually tying the distribution of matter-and-energy in the Universe to the gravitational effects experienced by matter and radiation within it, this new formulation would lead to the development of general relativity: still our best current theory of gravity some 109 years after it was first unleashed on the world.

Fixing the incompleteness between Newtonian gravity and special relativity was what led to the birth of general relativity.

The results of the 1919 Eddington eclipse expedition showed, conclusively, that the general theory of relativity described the bending of starlight around massive objects, overthrowing the Newtonian picture. This was the first observational confirmation of Einstein’s theory of gravity.

Over the course of the 20th century, quantum mechanics developed, largely driven by the properties of light, charged particles, and nuclear decays. Particles such as protons and neutrons were discovered within the atomic nucleus, while electrons were discovered orbiting them within atoms. The incompleteness between early formulations of quantum mechanics and special relativity led to the development of relativistic quantum mechanics, first explored by Dirac, and later to the development of the quantum theory of electrodynamics: by Feynman, Schwinger, and Tomonaga, among others.

Meanwhile, radioactivity, discovered by Becquerel and the Curies, led to the discovery of two types of interaction at play within the atomic nucleus: the strong nuclear force, responsible for what were then called α-decays, and the weak nuclear force responsible for β-decays. The incompleteness associated with weak decays led Wolfgang Pauli to hypothesize the neutrino and later led Enrico Fermi to devise a theory explaining these weak decays. Meanwhile, Hideki Yukawa developed a theory of the strong nuclear force, with subsequently discovered particles leading to the theory of quarks and color charges within protons and neutrons.

This illustration shows 5 of the main types of radioactive decays: alpha decay, where a nucleus emits an alpha particle (2 protons and 2 neutrons), beta decay, where a nucleus emits an electron, gamma decay, where a nucleus emits a photon, positron emission (also known as beta-plus decay), where a nucleus emits a positron, and electron capture (also known as inverse beta decay), where a nucleus absorbs an electron. These decays can change the atomic and/or mass number of the nucleus, but certain overall conservation laws, like energy, momentum, and charge conservation, must still be obeyed. Beta decay always involves a neutron, whether free or within a nucleus, decaying into a proton, electron, and electron antineutrino.

But it was the fundamental incompatibility of Fermi’s theory of the weak nuclear force with Feynman, Schwinger, and Tomonaga’s theory of quantum electrodynamics that led to the vital advance of what we now know as electroweak theory: the unification between the electromagnetic force and the weak force. Developed by Steven Weinberg, Shelly Glashow, and Abdus Salam, this new theory made use of the concept of spontaneous symmetry breaking and what’s now known as the Higgs mechanism, and predicted the existence of the massive bosons of the Standard Model: the W-and-Z bosons, as well as the Higgs boson.

Alongside the development of quantum chromodynamics and the concept of asymptotic freedom, these advances led to the current picture we have of the three quantum forces and fields that govern the Universe: the modern Standard Model of particle physics. It was a series of incompletenesses:

• the incompleteness of non-relativistic quantum mechanics with special relativity,
• the incompleteness of classical electromagnetism with quantum theory,
• the incompleteness of radioactivity with the conservation of energy,
• and the incompleteness of quantum electrodynamics with the weak nuclear force,

that gave rise to our modern picture of the quantum universe, complete with quantum fields and incorporating the strong, weak, and electromagnetic forces all into the same unified framework.

On the right, the gauge bosons, which mediate the three fundamental quantum forces of our Universe, are illustrated. There is only one photon to mediate the electromagnetic force, there are three bosons mediating the weak force, and eight mediating the strong force. This suggests that the Standard Model is a combination of three groups: U(1), SU(2), and SU(3), whose interactions and particles combine to make up everything known in existence. With gravity thrown into the mix, there are a total of 26 fundamental constants required to explain our Universe, with four big questions still awaiting explanation.

Incompletenesses also play an enormous role when it comes to our view of cosmology as well. The very idea of the Big Bang itself, as powerful as it is, comes along with its own set of incompletenesses. First brought to prominence by Bob Dicke in the 1970s, the extrapolation of our expanding, matter-and-radiation-rich Universe back to an arbitrarily hot, dense, uniform initial state came along with its own puzzles. In particular, such an early state:

• should have disconnected regions that have not had time to come to thermal equilibrium, rather than the same temperature everywhere as we observe,
• has no explanation for why it was initially so finely-tuned as to not immediately recollapse or expand rapidly into oblivion,
• and has no explanation for why there are no leftover, ultra-high-energy relics from this period within our observable Universe.

It was by considering those incompletenesses — known respectively as the horizon, flatness, and monopole problems — that the theory of cosmic inflation was developed: the theory that explains what preceded and set up the conditions for the hot Big Bang to occur. As new predictions were teased out of the theory, and spectacularly confirmed, inflation owes its origins to the considerations of these incompletenesses, as the historical record has preserved.

The logbook of Alan Guth, the theoretical physicist who is generally credited as the originator of the theory of cosmic inflation, details the moment he had the idea for the theory: inspired by considering mechanisms for solving various incompletenesses with the hot Big Bang.

Of course, there have been a great many ideas in theoretical physics that are motivated by further incompletenesses, but only a fraction of them have borne fruit. For example:

• the observed matter-antimatter asymmetry in our Universe, which cannot be explained by the Standard Model of particle physics and cosmology alone, is a known incompleteness,
• the large difference between the Planck mass and the observed masses of the fundamental particles in the Standard Model of particle physics is a known incompleteness,
• the fundamental incompatibility of quantum physics with Einstein’s (classical) theory of gravity, general relativity, is a known incompleteness,
• and the fact that inflation, while it explains the origin of the hot Big Bang, cannot itself be extrapolated back indefinitely, is another known incompleteness,

but that all of these incompletenesses have not yet led to an advance beyond our current understanding. They highlight several of the greatest unsolved problems in theoretical physics today, but many of the great ideas that have been proposed to fix these incompletenesses — including grand unification, supersymmetry, and string theory — have not led to any successful predictions for what ought to then be observed and measured in experiments.

The Standard Model particles and their supersymmetric counterparts. Slightly under 50% of these particles have been discovered, and just over 50% have never shown a trace that they exist. Supersymmetry is an idea that hopes to improve on the Standard Model, but it has yet to achieve the all-important ‘step 3’ in the three steps for supplanting the prevailing scientific theory: having its new predictions borne out by experiment.

Some of the incompletenesses in physics simply must have a solution. Matter exists copiously throughout the Universe, while antimatter does not, and therefore there must be some way that matter (and not an equivalent amount of antimatter) was generated in the past. Dark matter exists as well, and is required by a large suite of cosmological evidence; some particle, fluid, field, or phenomenon must account for it. Dark energy also demands an explanation, as the accelerated expansion of the Universe is an observational fact, one that persists even irrespective of the so-called Hubble tension.

But other incompletenesses may simply be facts about our Universe that don’t have a deeper explanation. There may not be any further unification of forces over and above what we know, and gravity may not even be an inherently quantum force in nature. There may not be a fundamental, underlying reason behind why the particle masses have the values that they do; they may simply be a set of constants that have no deeper explanation. And many aspects of our Universe have already proven to be fundamentally asymmetric in a way that appears incomplete, such as:

• all neutrinos being left-handed and all antineutrinos being right-handed,
• the existence of positive and negative electric (monopole) charges but not north and south magnetic (monopole) charges,
• and the fact that we have three spatial dimensions but only one time dimension,

and yet attempting to “complete” these theories by symmetrizing them and hypothesizing additional entities is wrongheaded; our Universe does not possess them.

Nature is not symmetric between particles/antiparticles or between mirror images of particles, or both, combined. Neutrinos, for example, are always left-handed, in that if you point your thumb in their direction of motion, they spin in the direction that your left hand’s fingers curl. Similarly, antineutrinos are always right-handed. Prior to the detection of neutrinos, which clearly violate mirror-symmetries, weakly decaying particles offered the only potential path for identifying P-symmetry violations.

Still, anytime you have an incompleteness in your theory, science compels you to explore it. At a fundamental level, one of the questions we often ask about reality is, “Since we observe this thing that exists, what could be the mechanism that caused it to become this way?” Sometimes, there is no mechanism. Sometimes, it truly is just the outcome of random chance, or happens to be the way things are.

But if you want to have any hope of making an advance in physics, you have to look for a mechanism. You have to suggest some way that the observed conditions could have arisen as a consequence of the rules governing them. Many advances throughout the history of science, from Newton’s law of universal gravitation (which set up the heliocentric, Keplerian solar system) to cosmic inflation (which set up the conditions present at the start of the hot Big Bang), have come about in exactly this fashion. The alternative — to claim things simply are the way they are — may in fact be true, but it’s tantamount to giving up on what we call dynamics: the idea that the Universe is explicable through science.

For all of the problems that many of our great, speculative ideas in theoretical physics may possess, at least they actually are ideas, and potential solutions to these great puzzles. Until the day arrives when humans are no longer curious about the puzzles that nature sets before us, physicists simply won’t be able to leave an incomplete theory alone.