Ask Ethan: What would magnetic monopoles mean for our Universe?
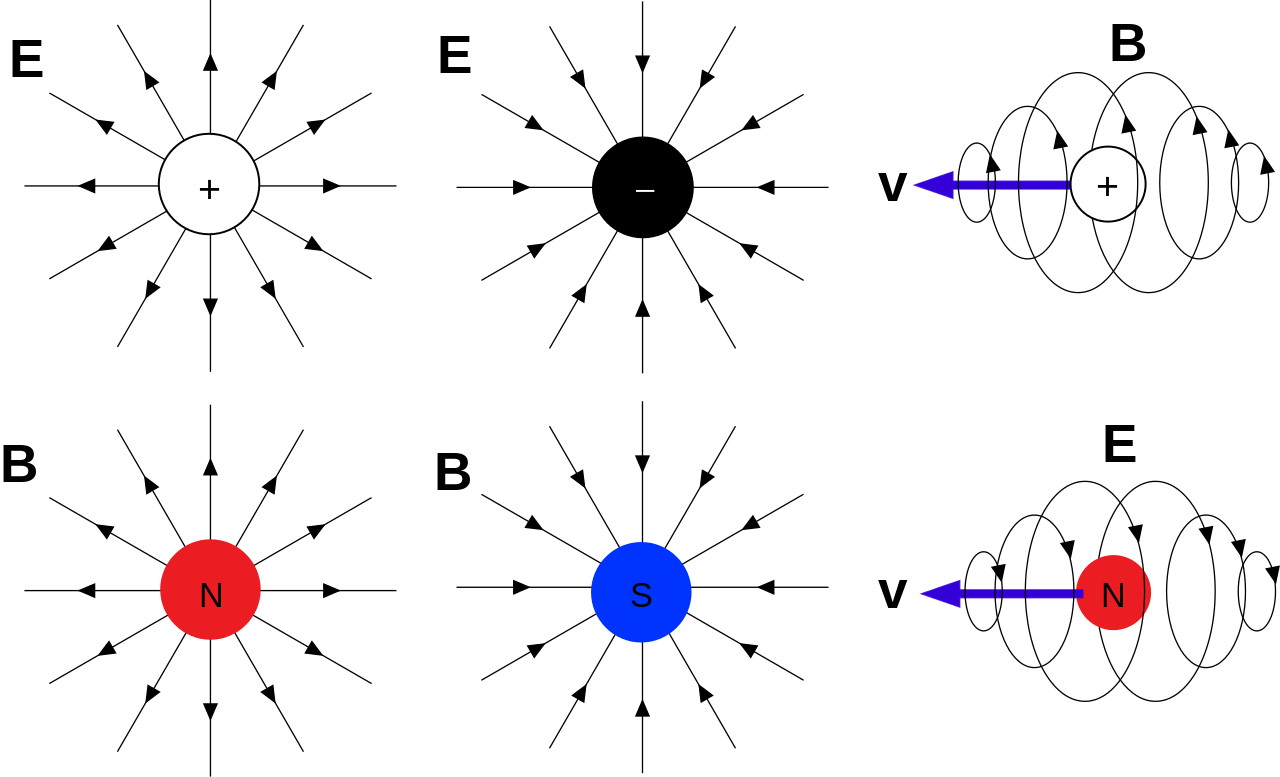
- In our Universe, we have plenty of electric charges, both positive and negative, but there’s never been a robust detection of a fundamental magnetic charge.
- These magnetic monopoles could exist, in theory, with a wildly fascinating set of consequences for our Universe if they do.
- Even though we still haven’t seen one, they’re a possibility that must remain under consideration for open-minded physicists everywhere. Here’s what everyone should know.
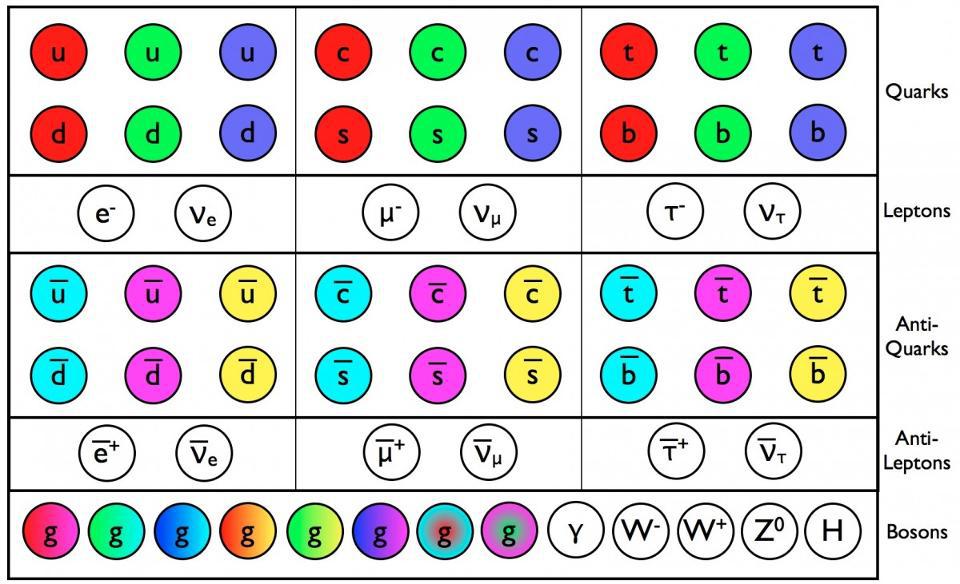
Out of all of the known particles — both fundamental and composite — there are a whole slew of properties that emerge. Each individual quantum in the Universe can have a mass, or they can be massless. They can have a color charge, meaning they couple to the strong force, or they can be chargeless. They can have a weak hypercharge and/or weak isospin, or they can be completely decoupled from the weak interactions. They can have an electric charge, or they can be electrically neutral. They can have a spin, or an intrinsic angular momentum, or they can be spinless. And if you have both an electric charge and some form of angular momentum, you’ll also have a magnetic moment: a magnetic property that behaves as a dipole, with a north end and a south end.
But there are no fundamental entities that have a unique magnetic charge, like a north pole or south pole by itself. This idea, of a magnetic monopole, has been around for a long time as a purely theoretical construct, but there are reasons to take it seriously as a physical presence in our Universe. Patreon supporter Jim Nance writes in because he wants to know why:
“You’ve talked in the past about how we know the universe didn’t get arbitrarily hot because we don’t see relics like magnetic monopoles. You say that with a lot of confidence which makes me wonder, given that no one has ever seen a magnetic monopole or any of the other relics, why are we confident that they exist?”
It’s a deep question that demands an in-depth answer. Let’s start at the beginning: going all the way back to the 19th century.
Little was known about electricity and magnetism at the start of the 1800s. It was generally recognized that there was such a thing as electric charge, that it came in two types, where like charges repelled and opposite charges attracted, and that electric charges in motion created currents: what we know as “electricity” today. We also knew about permanent magnets, where one side acted like a “north pole” and the other side like a “south pole.” However, if you broke a permanent magnet in two, no matter how small you chopped it up, you’d never wind up with a north pole or a south pole by itself; magnetic charges only came paired up in a dipole configuration.
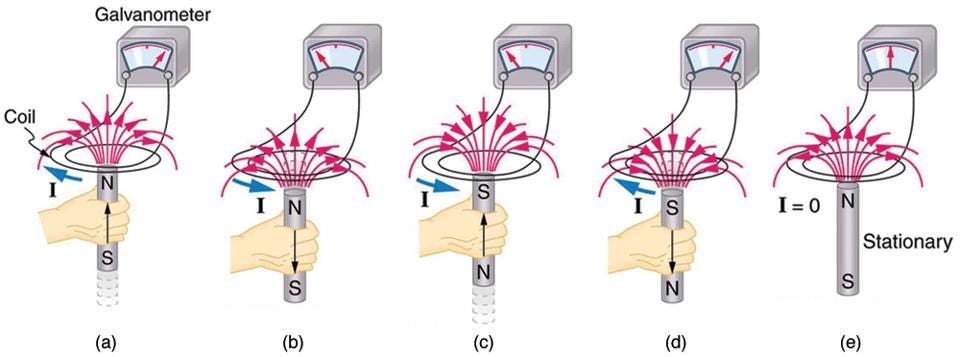
Throughout the 1800s, a number of discoveries took place that helped us make sense of the electromagnetic Universe. We learned about induction: how moving electric charges actually generate magnetic fields, and how changing magnetic fields, in turn, induce electric currents. We learned about electromagnetic radiation, and how accelerating electric charges can emit light of various wavelengths. And when we put all of our knowledge together, we learned that the Universe wasn’t symmetric between electric and magnetic fields and charges: Maxwell’s equations only possess electric charges and currents. There are no fundamental magnetic charges or currents, and the only magnetic properties we observe come about as being induced by electric charges and currents.
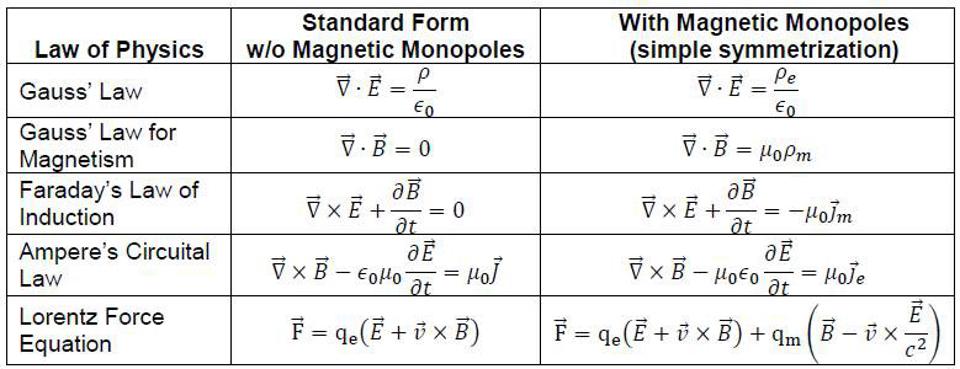
Mathematically — or if you prefer, from a theoretical physics perspective — it’s very easy to modify Maxwell’s equations to include magnetic charges and currents: simply add in the ability for objects to also possess a fundamental magnetic charge: an individual “north” or “south” pole inherent to an object itself. When you introduce those extra terms, Maxwell’s equations get a modification, and become completely symmetric. All of a sudden, induction now works the other way as well: moving magnetic charges would generate electric fields, and a changing electric field can induce a magnetic current, causing magnetic charges to move and accelerate within a material that can carry a magnetic current.
All of this was simply fanciful consideration for a long time, until we started to recognize the roles that symmetries play in physics, and the quantum nature of the Universe. It’s eminently possible that electromagnetism, at some higher energy state, was symmetric between electric and magnetic components, and that we live in a low-energy, broken symmetry version of that world. Although Pierre Curie, in 1894, was one of the first to point out that magnetic “charges” could exist, it was Paul Dirac, in 1931, who showed something remarkable: that if you had even one magnetic charge, anywhere in the Universe, then it quantum mechanically implied that electric charges should be quantized everywhere.
This is fascinating, because not only are electric charges observed to be quantized, but they’re quantized in fractional amounts when it comes to quarks. In physics, one of the most powerful “hints” we have that new discoveries might be around the corner are by discovering a mechanism that could explain why the Universe has the properties we observe it to have.
However, none of that provides any evidence that magnetic monopoles actually do exist, it simply suggests that they might. On the theoretical side, quantum mechanics was soon superseded by quantum field theory, where the fields are also quantized. To describe electromagnetism, a gauge group known as U(1) was introduced, and this is still used at the present. In gauge theory, the fundamental charges associated with electromagnetism will be quantized only if the gauge group, U(1), is compact; if the U(1) gauge group is compact, however, we get magnetic monopoles anyway.
Again, there might turn out to be a different reason why electric charges have to be quantized, but it seemed — at least with Dirac’s reasoning and what we know about the Standard Model — that there’s no reason why magnetic monopoles shouldn’t exist.

For many decades, even after numerous mathematical advances, the idea of magnetic monopoles remained only a curiosity that hung around in the back of theorists’ minds, without any substantial progress being made. But in 1974, a few years after we recognized the full structure of the Standard Model — which in group theory, is described by SU(3) × SU(2) × U(1) — physicists started to entertain the idea of unification. While, at low energies, SU(2) describes the weak interaction and U(1) describes the electromagnetic interaction, they actually unify at energies of around ~100 GeV: the electroweak scale. At those energies, the combined group SU(2) × U(1) describes the electroweak interactions, and those two forces unify.
Is it possible, then, that all of the fundamental forces unify into some larger structure at high energies? They might, and thus the idea of Grand Unified Theories began to come about. Larger gauge groups, like SU(5), SO(10), SU(6), and even exceptional groups began to be considered. Almost immediately, however, a number of unsettling but exciting consequences began to emerge. These Grand Unified Theories all predicted that the proton would be fundamentally stable and would decay; that new, super-heavy particles would exist; and that, as shown in 1974 by both Gerard t’Hooft and Alexander Polyakov, they would lead to the existence of magnetic monopoles.
Now, we have no proof that the ideas of grand unification are relevant for our Universe, but again, it’s possible that they do. Whenever we consider a theoretical idea, one of the things we look for are pathologies: reasons that whatever scenario we’re interested in would “break” the Universe in some way or another. Originally, when t’Hooft-Polyakov monopoles were proposed, one such pathology was discovered: the fact that magnetic monopoles would do something called “overclose the Universe.”
In the early Universe, things are hot and energetic enough that any particle-antiparticle pair you can create with enough energy — via Einstein’s E = mc² — will get created. When you have a broken symmetry, you can either give a non-zero rest mass to a previously massless particle, or you can spontaneously rip copious numbers of particles (or particle-antiparticle pairs) out of the vacuum when the symmetry breaks. An example of the first case is what happens when the Higgs symmetry breaks; the second case could occur, for example, when the Peccei-Quinn symmetry breaks, pulling axions out of the quantum vacuum.
In either case, this could lead to something devastating.
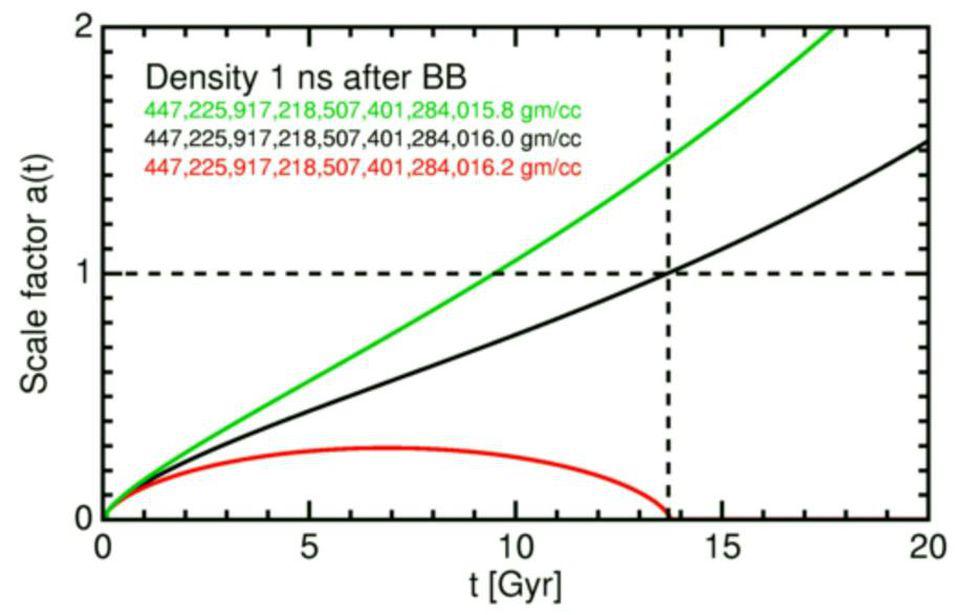
Normally, the Universe expands and cools, with the overall energy density being closely related to the rate of expansion at any point in time. If you either take a large number of previously massless particles and give them a non-zero mass, or you suddenly and spontaneously add a large number of massive particles to the Universe, you rapidly increase the energy density. With more energy present, suddenly the expansion rate and the energy density are no longer in balance; there’s too much “stuff” in the Universe.
This causes the expansion rate to not only drop, but in the case of monopole production, to plummet all the way to zero, and then to begin contracting. In short order, this leads to a recollapse of the Universe, ending in a Big Crunch. This is called overclosing the Universe, and cannot be an accurate description of our reality; we’re still here and things haven’t recollapsed. This puzzle was known as the monopole problem, and was one of the three main motivations for cosmic inflation.
Just as inflation stretches the Universe, whatever its geometry was previously, to a state indistinguishable from flat (solving the flatness problem), and imparts the same properties everywhere to all locations within our observable Universe (solving the horizon problem), so long as the Universe never heats back up to above the grand unification scale after inflation ends, it can solve the monopole problem, too.

This was understood way back in 1980, and the combined interest in t’Hooft-Polyakov monopoles, grand unified theories, and the earliest models of cosmic inflation led some people to embark on a remarkable undertaking: to try and experimentally detect magnetic monopoles. In 1981, experimental physicist Blas Cabrera built a cryogenic experiment involving a coil of wire, explicitly designed to search for magnetic monopoles.
By building a coil with eight loops in it, he reasoned that if a magnetic monopole ever passed through the coil, he’d see a specific signal due to the electric induction that would occur. Just like passing one end of a permanent magnet into (or out of) a coil of wire will induce a current, passing a magnetic monopole through that coil of wire should induce not only an electric current, but an electric current that corresponds to exactly 8 times the theoretical value of the magnetic monopole’s charge, owing to the 8 loops in his experimental setup. (If a dipole were to pass through, instead, there would be a signal of +8 followed shortly after by a signal of -8, allowing the two scenarios to be differentiated.)
On February 14, 1982, no one was in the office monitoring the experiment. The next day, Cabrera came back, and was shocked at what he observed. The experiment had recorded a single signal: one corresponding almost exactly to the signal a magnetic monopole ought to produce.
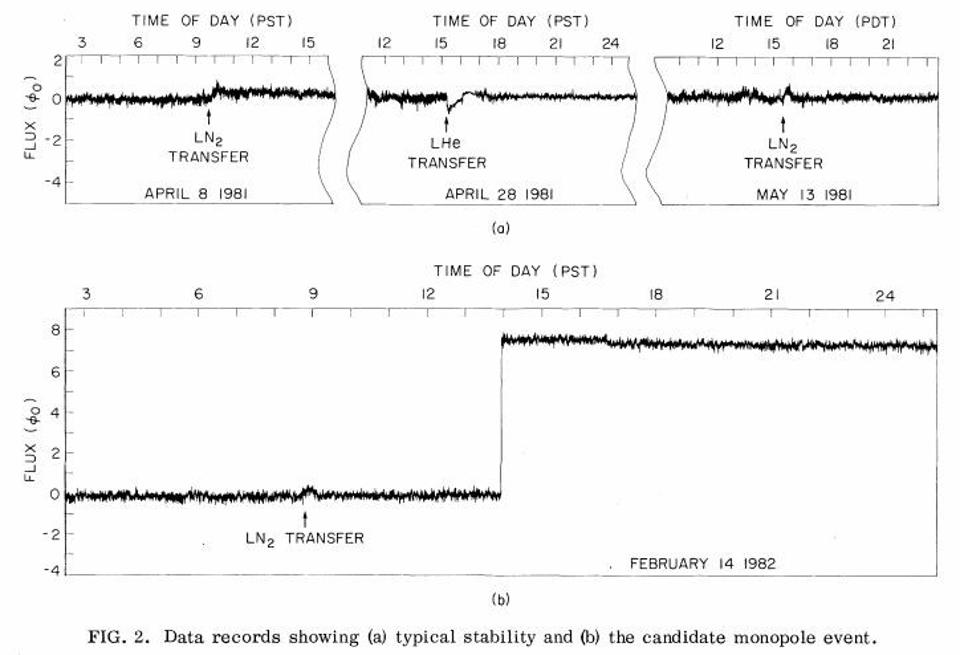
This set off a tremendous interest in the endeavor. Did it mean inflation was wrong, and we really did have a Universe with magnetic monopoles? Did it mean that inflation was correct, and the one (at most) monopole that should remain in our Universe happened to pass through Cabrera’s detector? Or did it mean that this was the ultimate in experimental errors: a glitch, a prank, or something else that we couldn’t explain, but was spurious?
A number of copycat experiments ensued, many of which were larger, ran for longer times, and had greater numbers of loops in their coils, but no one else ever saw anything that resembled a magnetic monopole. On February 14, 1983, Stephen Weinberg wrote a Valentine’s Day poem to Cabrera, which read:
“Roses are red,
Violets are blue,
It’s time for monopole
Number TWO!”
But despite all the experiments we’ve ever run, including some that have continued to the present day, there have been no other signs of magnetic monopoles ever seen. Cabrera himself went on to lead numerous other experiments, but we may never know what truly happened on that day in 1982. All we know is that, without the ability to confirm and reproduce that result, we cannot claim that we have direct evidence for the existence of magnetic monopoles.
There’s so much that we don’t know about the Universe, including what happens at energies far in excess of what we can observe in the collisions that take place at the Large Hadron Collider. We don’t know whether, at some high energy scale, the Universe can actually produce magnetic monopoles; we simply know that at the energies we can probe, we haven’t seen them. We don’t know whether grand unification is a property of our Universe in the earliest stages, but we do know this much: whatever occurred early on, it didn’t overclose the Universe, and it didn’t fill our Universe with these leftover, high-energy relics from a hot, dense state.
Does our Universe, at some level, admit the existence of magnetic monopoles? That’s not a question we can presently answer. What we can state with confidence, however is the following:
- there is an upper-limit to the temperature reached in the early stages of the hot Big Bang,
- that limit is set by constraints on the observations of gravitational waves which must be generated by inflation,
- and that if grand unification is relevant for our Universe, it is only permitted to occur at energy scales above that limit,
- meaning that if magnetic monopoles exist, they are required to have a very high rest mass: something on the order of 10¹⁵ GeV or higher.
It’s nearly 40 years since the one experimental clue hinting at the possible existence of magnetic monopoles simply dropped into our lap. Until a second clue comes along, however, all we’ll be able to do is tighten our constraints on where these hypothetical monopoles aren’t allowed to be hiding.
Send in your Ask Ethan questions to startswithabang at gmail dot com!