How ideas from physics drive AI: the 2024 Nobel Prize

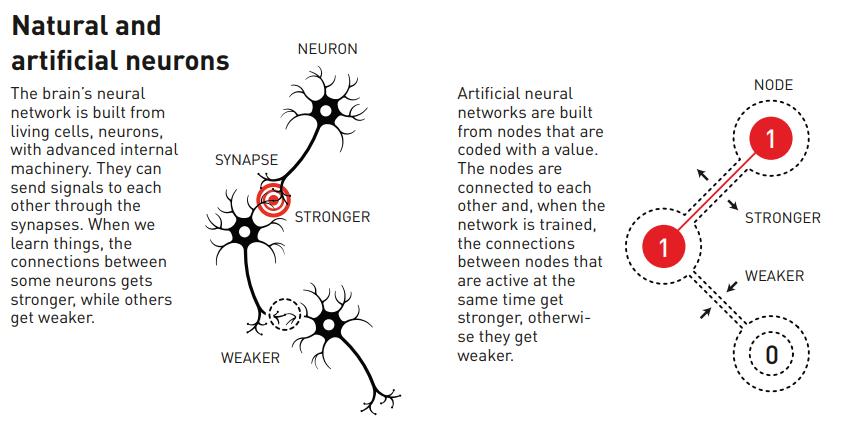
- The idea of an artificial neural network goes back to the 1940s: with the brain’s network of neurons and synapses modeled by a network of computationally connected nodes.
- By connecting biophysics with condensed matter physics systems (particularly involving particle spins), John Hopfield conjectured and found a model to link large collections of nodes to computational abilities.
- Building on Hopfield’s work, Geoffrey Hinton extended Hopfield’s model to a Boltzmann machine, with generative capabilities. Everything using AI and machine learning today relies on this Nobel-winning work.
When most of us think of AI, we think of chatbots like ChatGPT, of image generators like DALL-E, or of scientific applications like AlphaFold for predicting protein folding structures. Very few of us, however, think about physics as being at the core of artificial intelligence systems. But the notion of an artificial neural network indeed came to fruition first as the result of physics studies across three disciplines — biophysics, statistical physics, and computational physics — all fused together. It’s because of this seminal work, undertaken largely in the 1980s, that the widespread uses of artificial intelligence and machine learning that permeate more and more of daily life are available to us today.
The core of AI’s capabilities is rooted in the ability to recognize patterns within data, even incomplete or corrupted data. Our brains seem to do this automatically, but AI is capable of far surpassing, even in a generalized form, what even specialized and expertise-possessing humans cannot. Today, AI has scientific applications where it outstrips humans ranging from astronomy to medicine to particle physics, but its foundations go back to two pioneering physicists: John Hopfield, who developed a pioneering model for a practical artificial neural network, and Geoffrey Hinton, who used Hopfield’s work as the foundation for a new network, the Boltzmann machine, that would lead to today’s modern AI and machine learning programs. Here’s why their work deserves the 2024 Nobel Prize in Physics.

The idea that “artificial intelligence” would be related to physics, of all things, might seem far-fetched on the surface. “Why would a computer science breakthrough,” you might ask yourself, “be awarded the Nobel Prize in physics?” It’s a good question, of course, because the connection isn’t obvious on the surface. However, a look at three different subfields of physics:
- biophysics,
- statistical physics,
- and computational physics,
reveals an ultimately satisfying answer. In particular, the foundations of machine learning are based in statistical physics, and the idea that led to its birth — artificial neural networks — grew directly out of biophysics.
One of the holy grails of biophysics, or biology in general, is to understand how brains in general, and human brains in particular, work. While we’re arguably a very long way from understanding (or even having a consensus definition of) consciousness, we do have a basic understanding of the human brain. A mix of fats, salts, nerve cells, and glial cells, the brain relies on electricity. As electrical signals travel through the brain, they traverse a network of neurons and synapses. When multiple neurons fire together, or are stimulated at the same time, connections between them grow stronger, or are reinforced. Way back in 1949, neuropsychologist Donald Hebb put forth a theory of Hebbian learning: where it was exactly the stimulation of connections between neurons that led to the process of “learning” in living brains.

Therefore, it was reasoned that one could attempt to create an “artificial” brain, or at least something that was capable of learning to recognize patterns, by constructing a network that behaved similarly. The idea that emerged became known as an artificial neural network. In reality, an artificial neural network was simply a computer simulation, but a simulation where:
- you have nodes that can take on specific values, which represent neurons,
- and there are connections between nodes that can strengthen or weaken depending on if the nodes are stimulated together or not, which represent synapses.
Over time, if you stimulate connected nodes over and over again, connections will strengthen, while if you stimulate one when the other doesn’t stimulate (or vice versa), the connections will weaken.
Now, try to imagine the process of remembering something you heard, saw, or experienced long ago. I had this experience for myself a few months ago, watching an episode of the television show Don’t Forget the Lyrics, when they played the Rick James song Super Freak. It’s a song I’ve heard many times, and could’ve sworn I knew all the lyrics to, but when they stopped the music after:
“That girl is pretty wild now, the girl’s a super freak
the kind of girl ___ ___ ___ ___ ___ ___ ___“
I was stumped. I knew all sorts of lyrics to that song: that girl is pretty kinky, the girl’s a super freak; I really love to taste her, every time we meet, but that didn’t get me the answer. I tried humming the saxophone solo; that didn’t help. Then I tried singing the verse, and after, my brain went, that girl is pretty wild now, the girl’s a super freak, the kind of girl you read about, in new wave magazines. And then I exclaimed, “OH MY GOD, I AM THE SMARTEST MAN ALIVE!”

What just happened there? Is this a feeling you can relate to? As someone with a brain but with imperfect recall, this is illustrative of how our memories work: by stimulating the related parts of the brain, the parts that were stimulated when your memories were created and when you had recalled those memories (or that information) previously, you can trigger the stimulus for the part of the brain that “finds” the pattern you’re looking for. This big idea is known as associated memory: your brain not only stores patterns, but seeks to recreate them when you “remember” something that happened previously. This wouldn’t be obvious by looking at the individual neurons in your brain; it’s an emergent behavior that requires the various parts within it to act together.
This was the big idea that inspired John Hopfield: a physicist who had previously worked on problems in molecular biology, who then became interested in neural networks. Thinking about the collective behavior of neurons all firing together, he used an analogy with other physical systems that exhibited similar collective behavior: vortices that formed in flowing fluids and the direction in which atoms and molecules were oriented in magnetized systems. Hopfield conjectured that collective behavior in neurons could give rise to computational, or learning, abilities, and then sought to prove it by demonstrating this in an artificial neural network.
Hopfield began by creating an artificial neural network — again, just a computer program — where there were a large number of nodes, and where each node could take on only one of two values: 0 or 1. (Or, in analogue with magnetic spin, spin up or spin down.) Just as in the case of many magnetic materials, the value of the spins of the adjacent nodes (or atoms/molecules) would affect the value of the node (i.e., atom/molecule) in question, the value of the nodes in this neural network would be in part determined by the value of the connected nodes. Just as magnetized materials tend toward an equilibrium configuration, or a configuration where energy is minimized, Hopfield programmed his artificial neural network to minimize the energy across all nodes with respect to a series of pre-programmed patterns: what you might think of as a “training” data set.
Another way to think of this is to imagine that you have a grid that’s, say, 14 elements long by 19 elements high: with 266 elements total. There’s an “input pattern” that you start off with, and on its own, it might not look like anything. However, if you have a series of reference patterns (what you might call a “saved” pattern), the input pattern can be matched against all possible reference patterns to see which one is the closest match. This might proceed iteratively, where step-after-step refines your input pattern to better match close reference patterns. Even in cases where your input pattern is noisy, imperfect, or partially erased, you can often recover the best, most correct saved pattern that’s the best match for your input pattern.
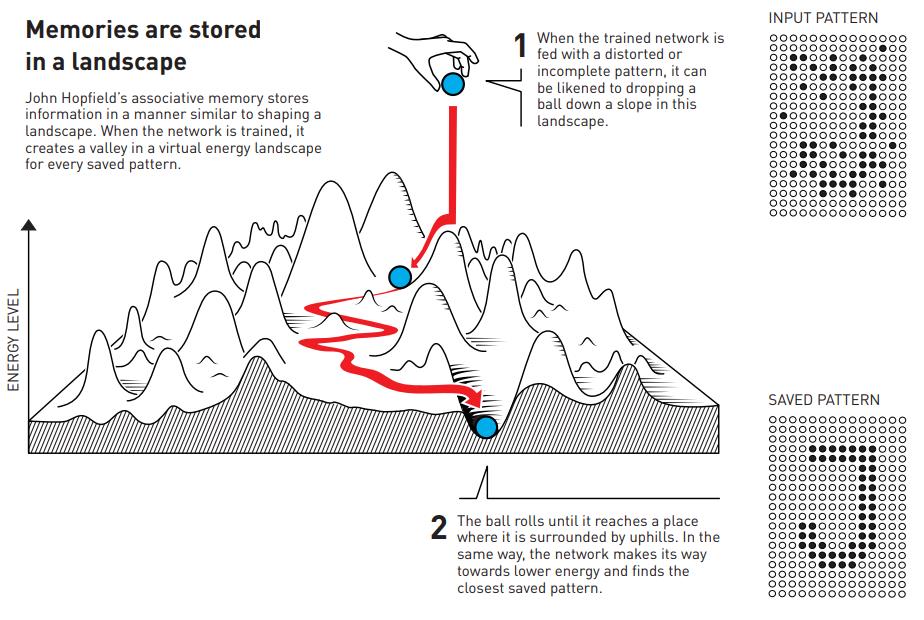
This rather primitive type of pattern-matching, which a Hopfield network is capable of performing, would pave the way for finding matches between even incomplete or corrupted data and a “true” reference data set, which still has applications in the realm of image analysis, including object recognition and computer vision. Still, Hopfield’s original model was fundamentally limited by whatever set of individual “saved patterns” were viewed as possible answers; it isn’t generative in nature, but can only pattern-match.
That’s where the work of Geoffrey Hinton — this year’s other Nobel Laureate in physics — comes in. Rather than focusing on specific individual patterns, it’s generalized to include a statistical distribution of patterns: including patterns that aren’t actually part of any reference data set. (For example, if your reference set includes only the 26 letters of the alphabet, you might also expect characters in your statistical distribution that represent multiple letters ligatured together, such as æ.) You might expect multiple possible solutions averaged together in some never-before-seen way to emerge from the data, such as a dotted “t” or a crossed “i” in text.
Hinton’s first big advance was to replace the primitive Hopfield model with the first true generative model: the Boltzmann machine.
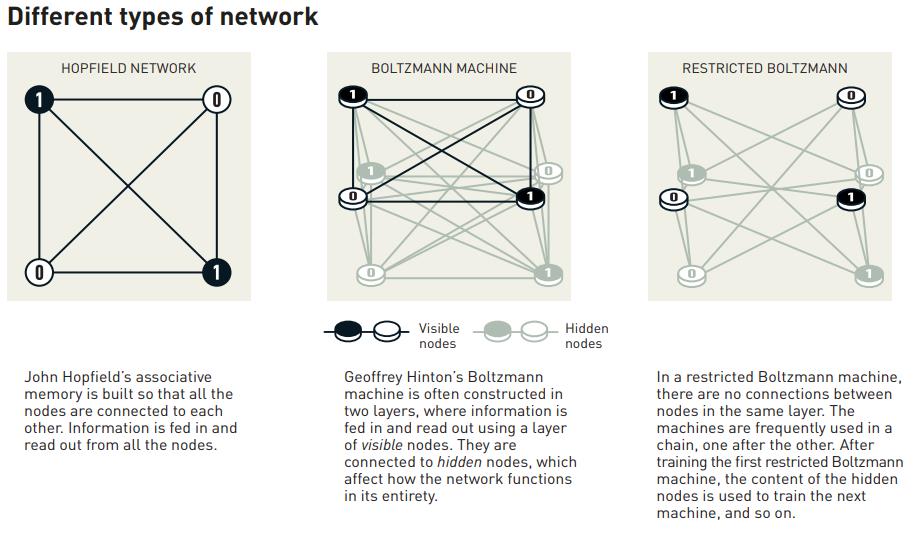
In a Boltzmann machine, you still have an input or a set of inputs that represents your initial data, and you still get an output or a set of outputs that represents what your computer program is going to read out to you at the end. However, in between the input and output layers, there can be a variety of hidden layers: where hidden nodes — nodes that not only aren’t part of any reference data set at all, but that weren’t inputted by a human (or a programmer) at any point along the line — separate the inputs from the outputs. These hidden layers allow for far more general probability distributions to be incorporated into the analysis, which may lead to unexpected outputs that no straightforward algorithm could ever have uncovered.
Although this type of computer, a Boltzmann machine, had limited applications because of how inefficiently its computing resources were leveraged, it led Hinton and other collaborators to a more streamlined model: the restricted Boltzmann machine, which:
- connected inputs to a hidden layer,
- where the hidden layer connects to another hidden layer before being connected to outputs,
- and then invokes backpropagation, where hidden layers can communicate with one another,
- before eventually converging on the optimal final output.
This advance was tremendously important for one profound reason: it demonstrated that networks with a hidden layer could be trained, by this method specifically, to perform tasks that had previously been demonstrated to be fundamentally unsolvable without such a hidden layer.

By restricting connections to being allowed between different types of nodes (input-hidden, hidden-output) but forbidden between nodes of the same type (input-input, output-output, or hidden-hidden of the same layer), the computational speedup and efficiency was profound. The importance, and function, of hidden nodes could no longer be denied.
Very swiftly, successful applications of this new technology began to be implemented. Banks could now classify handwritten digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) from checks automatically, without the need for human intervention. Patterns could be recognized in images, across languages, and even in clinical and medical data; one of the early advances that was unanticipated was the ability to identify “corner” features in images. Today, near-instantaneous and near-universal language translation is a technology we practically take for granted, but owes its roots to Hopfield and Hinton.
Later on, other methods were shown capable of replacing restricted Boltzmann machine-based pre-training, saving even more computing time while still enabling the same performance of deep and dense artificial neural networks.
Sure, the most widespread application of artificial neural networks now seem mundane: chatbots and text generators that fill the internet with confident declarations of dubious veracity, pre-programmed interactive “helpers” that waste your time while failing to solve your problems, “recommended” AI summaries that aggregate content but that frequently fail at their desired tasks. For all of the potential that artificial neural networks may have for our society, they’re often implemented in incredibly destructive, mind-numbingly banal fashions.
However, there are still tremendous applications that have actual positive values. Artificial neural networks excel at:
- being extremely good function approximators for even the most complicated mathematical functions,
- approximating many-body quantum systems that would be prohibitively computationally intensive to simulate exactly,
- modeling interatomic and intermolecular forces extremely well, enabling new predictions for certain classes of materials and the properties they should exhibit,
- and being extensible to complex physical systems.
The physical systems applications are enormous, and include physics-based climate models, searching for particle tracks that would indicate novel particles in accelerator-colliders (including the Higgs boson), mapping the Milky Way in neutrinos from the IceCube detector at the south pole, identifying transiting exoplanet candidates that human-based search algorithms miss, and even processing the data used to construct the Event Horizon Telescope’s first image of a black hole’s event horizon.

It is perhaps the biological and medical applications — in a perhaps ironic return to biophysics, the science that initiated humanity’s interest in artificial neural networks — that are most profound. AlphaFold can predictively compute fully folded protein structures, including tertiary and quaternary structures, based solely on the underlying amino acid sequence. Machine learning using artificial neural networks can greatly improve early detection of breast cancers (without increasing the false positive rate) based on mammographic screening images. And it’s the best tool we have for correcting for the voluntary and involuntary motions that occur in patients receiving an MRI scan on any part of the body.
While there are certainly going to be a large population of gatekeeping, naysaying physicists out there who’ll cry out, “This is computer science, it isn’t even physics,” it’s vital to keep in mind that the same things were once said about:
- chemical physics,
- biological physics (biophysics),
- computational physics,
- statistical physics,
and all sorts of other subfields of physics. People have derided the Nobel Prizes given to atomic clocks and timekeeping on similar grounds. The message to those who think that way is this: just because this field is an outgrowth of an aspect of physics that doesn’t interest you doesn’t mean it isn’t physics, and it certainly doesn’t mean that it isn’t Nobel-worthy. Whether we use AI, machine learning, and artificial neural networks in general for society’s good or society’s ill isn’t the point. The point is that this new and powerful technology is becoming more and more ubiquitous, and it was insights from physics that led to its inception and many of the great leaps in its capabilities. How we go from here is way out of the hands of the Nobel committee, just as Nobel himself, the inventor of dynamite and high explosives, was not in control of how his invention would later be used. The next steps, for all of humanity, are up to us.