Relativity: the oldest physics principle that’s still correct

When most people think of the term relativity, the first person who comes to mind is Albert Einstein. Indeed, Einstein’s two theories of relativity — the special theory of relativity, put forth in 1905, and the general theory of relativity, put forth a decade later in 1915 — represent a revolutionary way of viewing our Universe. Prior to Einstein, it was thought that both space and time were absolute quantities: the same for all observers, regardless of their location or of their motion through the Universe. It was thought that the amount of time that passed for anyone, anywhere, would be universally agreed upon, as would the distance between any two points or the physical size of solid objects. Only with the arrival of Einstein was it recognized that even quantities such as space and time weren’t absolute at all, but were instead experienced relative to the observer’s point of view.

But Einstein didn’t originate the concept of relativity at all. In fact, relativity can trace its origins back to nearly 400 years ago: when it was put forth by a scientist who obsessively studied the behavior of objects that moved long before even Newton’s laws of motion: Galileo Galilei. Relativity wasn’t about space or time when it was considered by Galileo, but instead about a much simpler concept: the detectability of motion. What was the difference between the two scenarios of:

• someone who was in a closed room, with no window to the outside, that was absolutely stationary with respect to everything around them,
• versus someone who was in an identical closed room, with no window to the outside, that was in constant, unchanging motion in some direction relative to the outside world?

Galileo’s great realization, encapsulated in the principle of relativity, is that there was no difference at all. This core principle of physics, first written down in 1632, remains unchanged, even to the present day.

Are these men on a train that’s stationary and at rest? Or is the train in constant motion relative to the outside world? If not for the sounds and vibrations of the train along the track, and the cues of the outside world seen through the windows, there would be no way for them to know, and no experiment they could perform inside the train car that would tell them. This is the key behind Galilean relativity.

Galileo’s thought process that led him to the principle of relativity was remarkable, yet simple at the same time. Galileo made many inquiries into motion over his life. His most famous discoveries were arguably astronomical, relating to the motions of objects in the heavens. He was familiar with the ideas of Copernicus, and was partial to the notion of a heliocentric Solar System, where Earth was just one of several ordinary planets — along with Mercury, Venus, Mars, Jupiter, and Saturn — that all orbited the Sun. When it came to the daily motion of the objects in Earth’s sky, however, Galileo noted that there were two possible explanations for why the Sun always appeared to rise in the east, pass overhead, and then set in the west, consistent with the observations that the planets, our Moon, the stars, as well as the entire night sky appeared to rotate about Earth’s north celestial pole.

1. It was possible that the entirety of the heavens — along with all of the objects that were in it — were rotating overhead, while the Earth remained stationary beneath it.
2. But it was also possible that the heavens themselves were stationary, and that it was actually planet Earth itself that was in motion: rotating about its axis, which gave the appearance of a “rotating sky” to an observer here on Earth.

Galileo noted that there was no experiment that one could reasonably perform here on Earth that would allow someone on the Earth to tell these two scenarios apart. Whether the Earth itself was stationary or whether the planet itself was spinning on its axis, rapidly, completing a full rotation once-per-day, was not something that someone on the Earth was capable of discerning by simply being here on the Earth itself.

Above the central array of the Atacama Large Millimetre/Submillimetre Array (ALMA), the southern celestial pole can be pinpointed as the point about which the other stars all appear to rotate. The length of the streaks in the sky can be used to infer the duration of this long-exposure photograph, as a 360 degree arc would correspond to a full 24 hours of rotation. This observed phenomenon could, in principle, be due either to the rotation of the heavens or to the rotation of the Earth.

Consider, for example, the popular, legendary (and perhaps apocryphal) experiment performed by Galileo: dropping balls off of the Leaning Tower of Pisa. If the Earth were stationary, it’s easy to predict what would happen. Galileo stands atop the tower, holding a ball, while the tower stands, unmoving, upon the stationary Earth. When Galileo drops the ball, it simply falls straight down, in a straight line, with its horizontal position never deviating from its initial location above the ground; only its vertical position would change as Galileo releases it, and gravity pulls it down.

But, now, what would happen if the Earth were rotating?

You might think that, if the Earth were spinning about its axis, that when Galileo dropped this ball, the ball would then be in free-fall, while the tower — anchored into the Earth — would rotate along with the Earth itself. If this occurred, perhaps:

• the ball would fall straight down, in a straight line, toward the center of the Earth,
• while the tower would continue rotating along with the Earth itself,
• which would result in the ball appearing to “separate” from the tower at the rate of Earth’s rotation.

Noting that the Earth was a sphere about 40,000 kilometers in circumference, that it rotated once every 24 hours, and that Pisa, where the tower was located, was roughly halfway between the equator and the North Pole, it’s fairly easy to calculate that the tower itself is in motion at around 330 meters-per-second relative to the center of the Earth. Since it takes a ball dropped from the (55-meter-tall) tower a little more than 3 seconds to hit the ground, the fact that the ball appears to fall straight down, rather than winding up over 1000 meters away, you might be tempted to conclude that this experiment proved that the Earth wasn’t rotating.

This Foucault pendulum, on display in action at the Ciudad de las Artes y de las Ciencias de Valencia in Spain, rotates substantially over the course of a day, knocking down various pegs (shown on the floor) as it swings and the Earth rotates. This demonstration, which makes the rotation of the Earth very clear, was only concocted in the 19th century: more than 200 years after the death of Galileo.

Many of Galileo’s contemporaries thought in precisely this fashion. Knowing that the Earth was a sphere with a well-measured circumference, they could calculate what rate the planet — and hence, everything on it — would be moving at if we were, in fact, spinning about our axis. They reasoned that once Galileo released that ball, the ball would be compelled to fall down to the surface of the Earth: straight down, and therefore the rotating Earth should carry the tower away from the ball. Since this wasn’t observed, that implied (to them) that the Earth couldn’t be rotating.

But Galileo thought about things differently: in relative terms to one another. Sure, the tower might be moving at around 330 meters-per-second relative to the center of the Earth, but so was everything else in this problem:

• the ground of Pisa itself,
• the tower,
• Galileo, standing atop the tower,
• the surrounding atmospheric air,
• and the ball in Galileo’s hand.

When Galileo releases this ball, it keeps its memory of that original motion across the surface of the Earth; nothing impacts or changes it when Galileo releases it, and so it doesn’t “separate” from the tower at all. Instead, it simply falls straight down. In fact, the only difference that could potentially be detected would be the fact that, since it’s anchored into the rotating Earth, the “top” of the tower moves slightly faster than the “bottom” of the tower, as it traces out a slightly greater-circumference circle around the Earth as the Earth rotates. The relative motion of the ball, once dropped, with respect to the bottom of the tower would be tiny — about 1.5 millimeters, total — or small enough that it would be unmeasurable with the technology available to Galileo at the time.

According to legend, the first experiment to show that all objects fell at the same rate, irrespective of mass, was performed by Galileo Galilei atop the Leaning Tower of Pisa. Any two objects dropped in a gravitational field, in the absence of (or neglecting) air resistance, will accelerate down to the ground at the same rate, and will traverse an amount of distance that’s proportional to the time it’s in free-fall squared. The ball does not “separate” from the tower, either, which some (incorrectly) expected would have been the case if the Earth rotates.

Why would Galileo think so differently than the rest of his contemporaries?

Perhaps the answer lies in the types of experiments that Galileo performed over the course of his life. Galileo was extremely interested in the motion of objects, and in particular, in the relationship between four quantities:

• distance,
• velocity,
• acceleration,
• and time.

However, simply “dropping balls” was too difficult, as there were no measuring devices at the time that were accurate enough to uncover the relationship between how much an object moved in a given amount of time when subjected to the gravitational acceleration here on Earth’s surface. Fortunately, Galileo had a trick up his sleeve, perhaps influenced by his music-oriented father.

Instead of using objects in free-fall, Galileo began rolling objects — balls and cylinders — down a very slightly inclined ramp. By controlling the inclination of the ramp, Galileo could control the speed of the ball: a ramp that was very close to horizontal would lead to objects accelerating only very slowly, stretching out the amount of time it took them to traverse the ramp. Without a timekeeping tool, Galileo instead set up thin wires, or strings, that would make a sound when the rolling object rolled over them. By spacing out the wires so that the “sounds” would occur at an even tempo, with equal amounts of time between the stimulation of each string, Galileo figured out the basics of the mechanics of motion: that the distance traveled by an object initially at rest was proportional to the amount of time squared that the object is accelerated over.

When a ball or cylinder begins at rest and then rolls down a hill, the amount of distance that it traverses is proportional to the square of the amount of time it’s been in motion for. This relationship was first uncovered by Galileo more than 400 years ago, and is taken advantage of in the modern-day extreme activity known as “Zorbing.”

But his next great insight went a step further. Galileo recognized that the experiments he was performing were yielding results that were completely agnostic about whether the room that he was in was in constant motion or not. Sure, there might not have been planes, trains, or automobiles for Galileo to travel in, but there was a type of vessel that was frequently in constant motion: a ship. Galileo recognized that he could perform these experiments — of rolling balls and cylinders down ramps — aboard a ship just as easily as he could on the surface of the Earth, and that there would be no way of telling, from the results of the experiment, whether the ship were safely docked ashore, or whether the ship was in motion, being carried by the current of the sea.

In fact, this was precisely the situation considered by Galileo in his 1632 book, Dialogue Concerning the Two Chief World Systems, where he related (as told in Matt Strassler’s book, Waves in an Impossible Sea),

“Shut yourself up with some friend in the main cabin belowdecks on some large ship… [and] a person belowdecks on a smoothly sailing ship cannot hope to determine whether the ship is in motion or, if so, what is its speed.”

This key insight — that someone in constant motion has no physical evidence of their motion except by comparing it relative to the outside world — is the core of the principle of relativity.

This picture shows US Coast Guard ship Cutter Munro departing from the docks in San Diego, CA. So long as this boat is not accelerating, an observer who is below the deck and has no window to the outside cannot tell whether their boat is stationary or in constant motion relative to the outside world.

What this version of relativity (Galilean relativity) tells us is that quantities like “position” or “distance,” as well as quantities like “velocity” or “speed,” are not absolute quantities that everyone agrees on. If Galileo were on a ship rolling balls and cylinders down a ramp, and that ship were in motion on the sea, then someone:

• on the ship with Galileo,
• on a buoy that were stationary relative to the motion of Galileo’s ship,
• or on a different ship that were in motion relative to Galileo’s ship,

would all make different measurements for the positions and speeds of the balls and cylinders rolling down Galileo’s ramp at any and all moments in time.

However, even though their measurements would be different from one another’s, no one would be wrong. The measurements would all be consistent with one another, and — assuming that all of these ships and observers were in constant, unchanging (i.e., non-accelerating) motion — they would all reach the same conclusions about matters like “What is the acceleration due to Earth’s gravity?” and “How much time passes between the successive stimulation of the strings along his ramp?” In Galilean relativity, positions and velocities are all dependent on the motion of the observer, but other quantities, like the distances between two points, the time between two events, or the acceleration due to gravity, remain invariant.

Different frames of reference, including different positions and motions, would see different laws of physics (and would disagree on reality) if a theory is not relativistically invariant. The fact that we have a symmetry under ‘boosts,’ or velocity transformations, tells us we have a conserved quantity: linear momentum. The fact that a theory is invariant under any sort of coordinate or velocity transformation is known as Lorentz invariance, and any Lorentz invariant symmetry conserves CPT symmetry. This notion of invariance under constant motion dates all the way back to the time of Galileo.

Remarkably, despite all the advances that we’ve made in physics in all the time since, including:

• the advent of Newton’s law of universal gravitation,
• the discovery of electromagnetism,
• the advances of special and general relativity,
• and the revolution of quantum mechanics and quantum field theory,

Galileo’s 1632 statement about relativity — that all observers in constant motion (or at rest) experience the same laws and rules governing reality — remains correct even today. At 392 years (and counting), it is arguably the oldest physical principle that remains true, today, in its original, unchanged form.

However, it’s important to recognize that three major aspects of relativity truly have changed in all the time since. The first two were discovered in the late 1800s and put on solid footing by Einstein in 1905: the notion that “distance” and “time” are not absolute quantities that are universally agreed upon between observers, but rather these, too, transform dependent on the relative motion of the observers in question. There are quantities that observers do universally agree upon — things like the value of the speed of light and a quantity known as the spacetime (or Einstein) interval — but things like “lengths” and “durations” are also relative.

A “light clock” will appear to run differently for observers moving at different relative speeds, but this is due to the constancy of the speed of light. Einstein’s law of special relativity governs how these time and distance transformations take place between different observers. However, each individual observer will see time pass at the same rate as long as they remain in their own reference frame: one second-per-second, even though when they bring their clocks together after the experiment, they’ll find that they no longer agree.

The third — and arguably, most profound — modification that needs to be made to Galilean relativity is that what we conceive of as “acceleration” is also not a constant that all observers agree on, but rather is a downstream consequence of the combined effects of any thrust or applied force, as well as the curvature of spacetime, which is the underlying cause of what we experience as gravitation. Distances (or lengths) and times (or durations) aren’t only affected by the motions of observers and objects relative to one another, but are also affected by the curvature of spacetime, which is itself determined by the distribution of matter and energy throughout the Universe.

One fun experiment you can do — even as a child — to experience this for yourself is to jump, from rest, as high as you can, inside of a closed elevator. If you do this when the elevator is at rest, you’ll reach a maximum height above the floor, and come down (for most people) after about 1 second has passed. If you do this when the elevator is moving down (at a constant speed) or up (at a constant speed), you’ll have the same exact experience as you did when the elevator was at rest. But if you instead jump when:

• the elevator accelerates upward from rest,
• the elevator accelerates downward from rest,
• the elevator decelerates toward rest while moving upward,
• or the elevator decelerates toward rest while moving downward,

both your maximum height above the floor and the amount of time you spend in the air will be different. (Be careful not to hit your head on the top of the elevator if you do this!)

The identical behavior of a ball falling to the floor in an accelerated rocket (left) and on Earth (right) is a demonstration of Einstein’s equivalence principle. If inertial mass and gravitational mass are identical, there will be no difference between these two scenarios. This has been verified to better than ~1 part in one trillion for matter through torsion balance experiments, and was the thought (Einstein called it “his happiest thought”) that led Einstein to develop his general theory of relativity. Recently, the ALPHA-g experiment confirmed that this is true for antimatter as well.

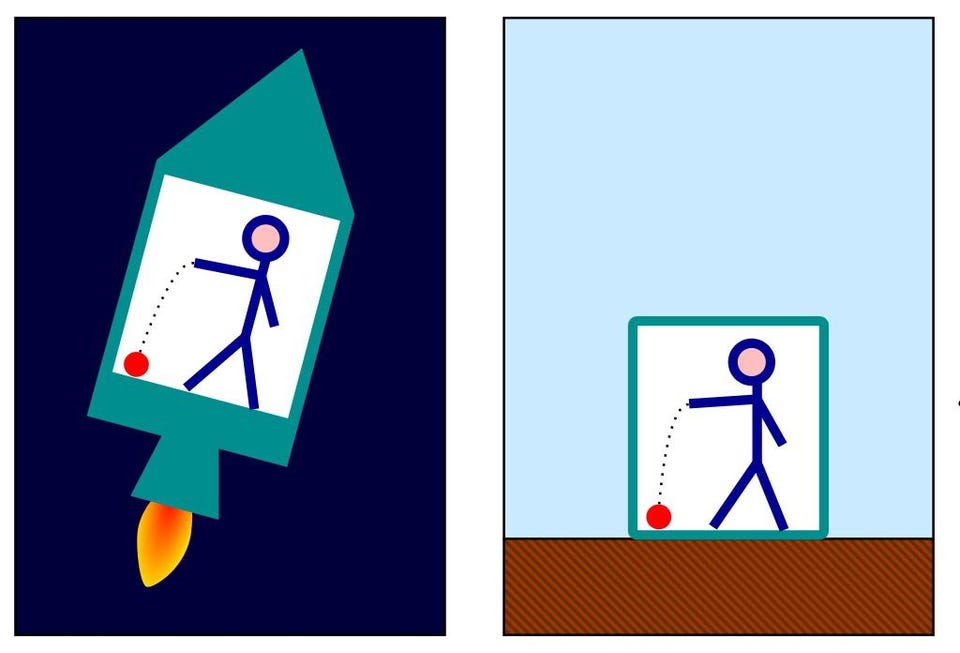
But the original principle of relativity’s core application still remains. Observers who experience themselves to be at rest on the surface of the Earth have no way of telling, without making some reference or measurement to the outside world, whether they are, in fact, at rest, or whether they’re in constant, uniform (non-accelerating) motion.

Additionally — and this is not only a consequence of general relativity, but was Einstein’s original inspiration for it — if you are experiencing an acceleration (say, downward), you have no way of detecting whether this acceleration is due to the thrust of your engines or whether it’s due to the force of gravity. These two scenarios, illustrated above, led Einstein to formulate what’s now known as his equivalence principle. Observers in a closed room on Earth versus observers in an accelerating rocket in space have no way of telling which situation describes their experience without looking to the outside world.

Today, we understand that many of the laws and rules obeyed by the Universe are unchanged by our positions and motions as we experience it. But the origin of relativity, and the notion that constant motion and being at rest are physically indistinguishable scenarios, goes back nearly 400 years. After all these centuries, we should still find ourselves thanking Galileo.

The author acknowledges Matt Strassler’s excellent popular book, Waves in an Impossible Sea, for relating the Galilean origin of relativity.