The Strong Nuclear Force Made Easy: Without Colors Or Group Theory

If you’ve ever struggled with the strong force, this explanation is a life-saver.
If you ask someone to think about some physical phenomenon that’s responsible for any sort of force in the Universe, you’re likely to get one of two answers. Either the person will answer gravity — the attractive force between all objects with mass or energy — or they’ll list any other force that we typically encounter between atoms on Earth, all of which are some variation on the electromagnetic force. Either there’s an attractive force between two particles with mass-or-energy, as in gravitation, or there’s an attractive or repulsive force between systems of charged particles either at rest or in motion, as in electromagnetism.
But there are other forces in the Universe that are arguably at least as important for creating the collections of matter and energy that exist in the Universe: the nuclear forces. After all, it’s the atomic number of every atom, also known as the number of protons in its nucleus, that determines the physical and chemical properties of all the normal matter on Earth and elsewhere in the Universe. And yet, without the strong nuclear force, the repulsive force between the positively charged protons in every nucleus heavier than hydrogen would destroy it instantly. Here’s how the strong force works to hold the building blocks of matter together.
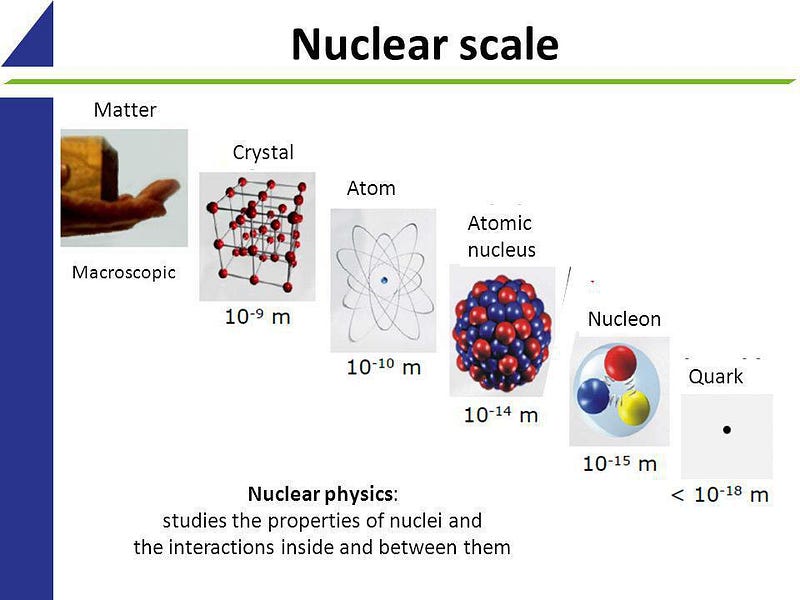
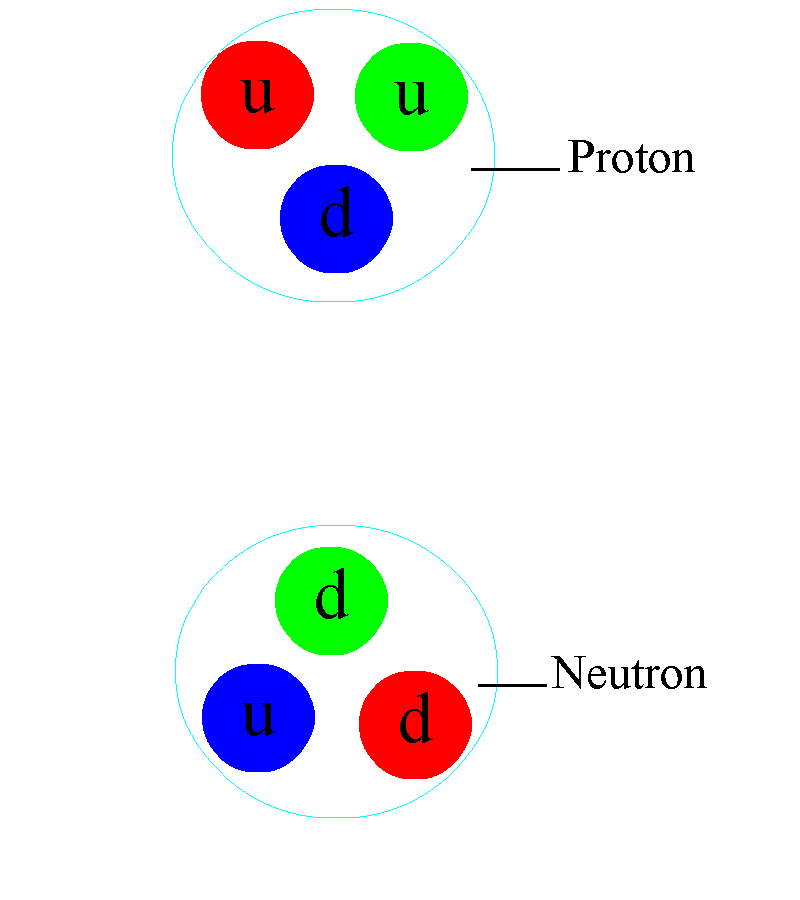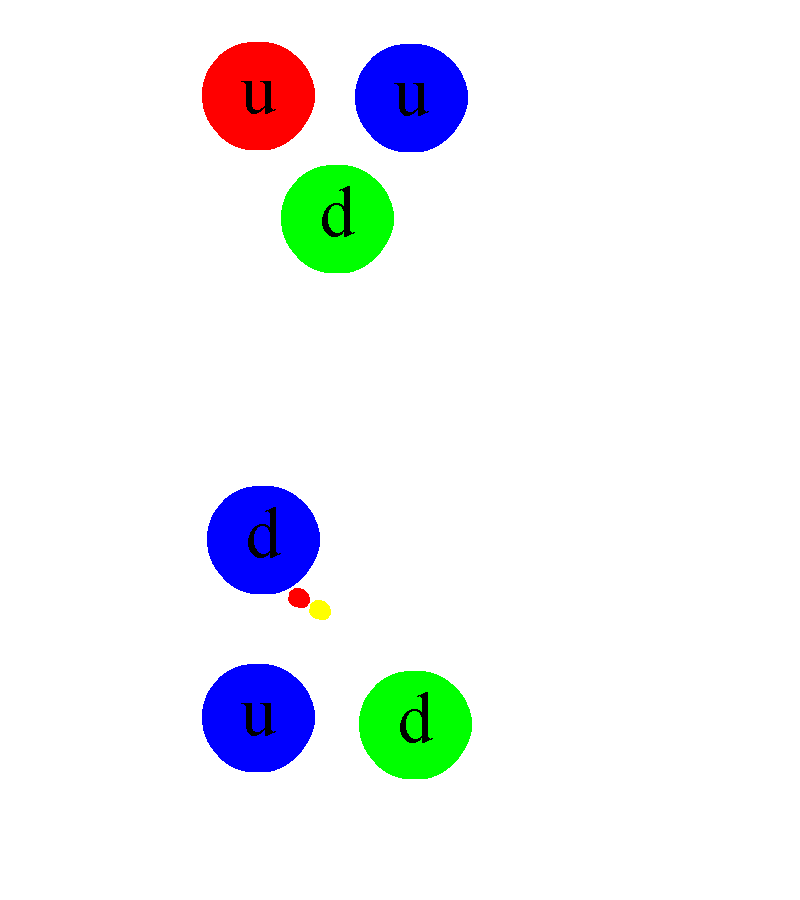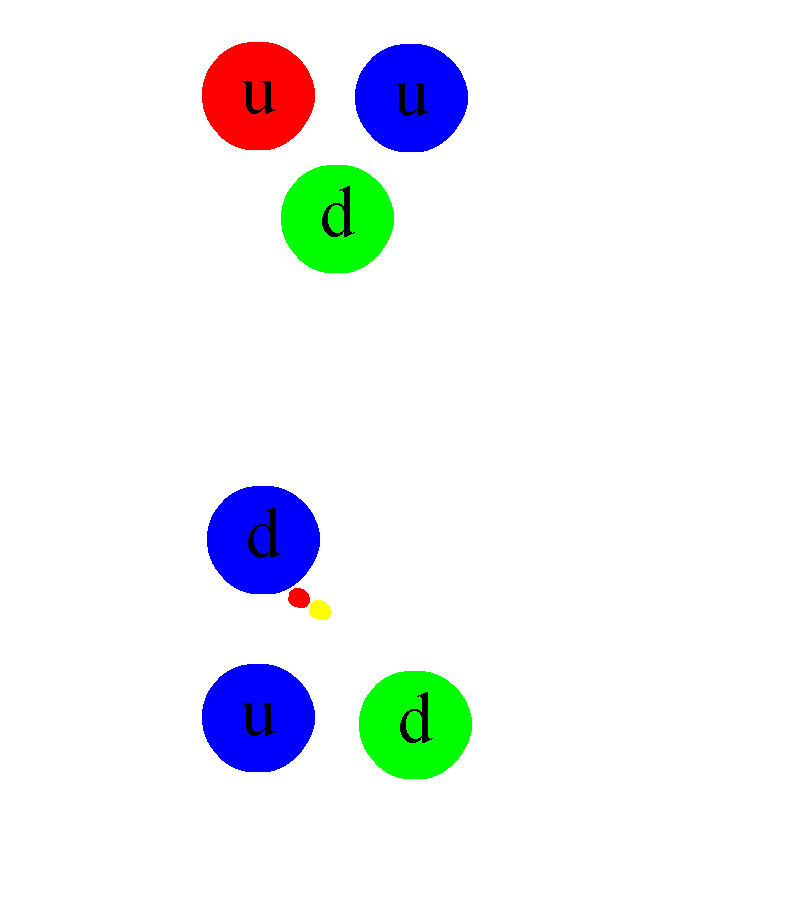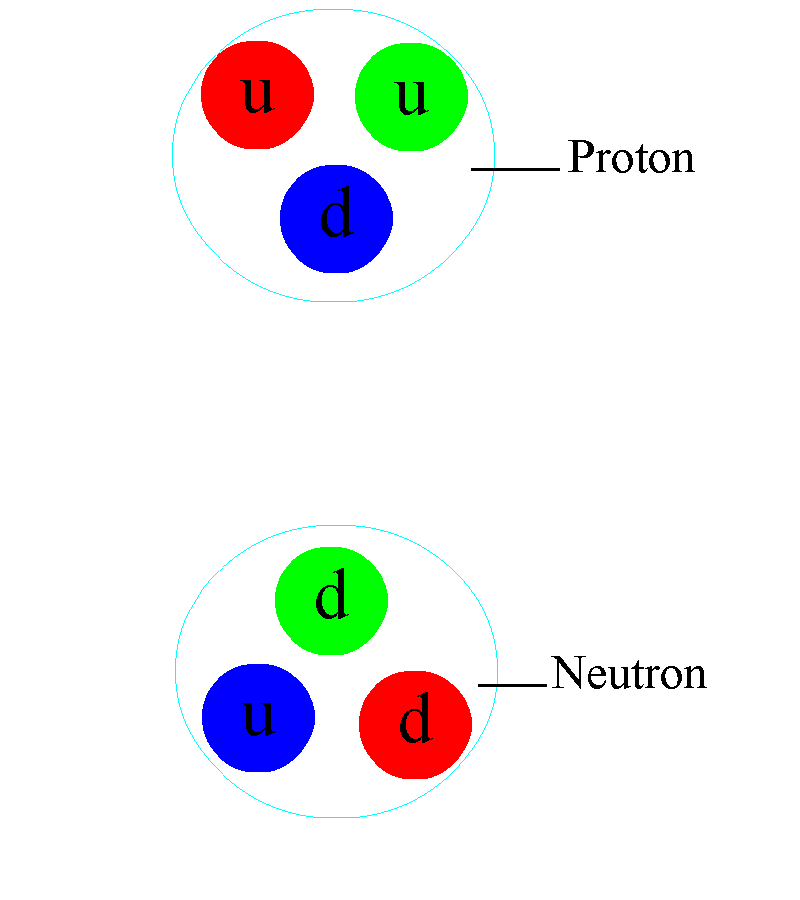
The first thing you have to understand is that atomic nuclei — what we typically think of as a combination of protons and neutrons — are actually a lot more complex than just a collection of two types of particles. Protons and neutrons are distinct: protons are electrically positively charged, stable in isolation, and have a very specific mass; neutrons are electrically neutral, unstable in isolation (they will decay with a half-life of about 10 minutes), and are about 0.14% heavier than protons are. And it’s true: that protons and neutrons, bound together in various combinations, make up all of the elements and isotopes found in nature.
But it’s also true that neither protons nor neutrons are fundamental particles. Inside each proton are three quarks: two up and one down quark, bound together through the physics of the strong nuclear force. Similarly, each neutron also has three quarks: two down quarks and one up quark, similarly bound through the strong force.
As you’ve already guessed, the strong force is fundamentally different from gravitation and electromagnetism in a number of ways. The first is this: whereas gravitational and electromagnetic forces both get stronger as two “charges” get closer together, the strong force actually drops to zero at extremely short distances.
If you halve the distance between two masses, the gravitational force quadruples or even more-than-quadruples, like if you’re in a strong gravitational field around a black hole or neutron star. If you halve the distance between two electric charges, the electrostatic force quadruples, with like charges repelling one another with four times the original force and opposite charges attracting one another similarly.
The strong force is like gravity in the sense that it’s always attractive, but in every other respect, it’s tremendously different from both gravity an electromagnetism. For instance, if you were to halve the distance between two of the quarks inside a proton or neutron, the force not only doesn’t quadruple, but actually drops: becomes smaller than it was back when the distance was greater. In fact, if you went in the opposite direction and increased the distance between these particles, the (attractive) force actually increases in strength.
This means that there’s a particular separation distance between the quarks that’s ideal: where the repulsive electric forces and the attractive strong force balance out. This explains why the proton and neutron have particular sizes to them, where each one has a radius that’s a little smaller than a femtometer. The strong force isn’t “an attractive pit” like gravity is, but rather is like a Chinese finger trap: the force increases as you pull quarks apart, but goes to zero if you bring them close enough together.

So what makes the strong force works the way it does? Normally, physicists give the answer in one of two ways. Either they go into the intricate mathematics of group theory — specifically the special unitary group SU(3) — to derive the relationships between quarks and the force-carriers of the strong force, gluons, or they use the flawed, but useful, analogy of colors.
Fortunately, we don’t have to go to such complex lengths to understand the strong nuclear force. All we have to do is recognize the other fundamental difference between gravity, electromagnetism, and the strong nuclear force: the way “charges” work in these theories.
- In gravitation, there’s only one type of “charge” that exists: positive mass and energy. If you have either mass or energy (or both), you’ll attract every other mass or energy in the Universe.
- In electromagnetism, there are two types of charges: positive and negative electric charges. Like charges repel, opposite charges attract, and charges in motion generate magnetic fields, which can attract or repel one another and change a moving charged particle’s direction.
- But in the strong force, there are three fundamental types of charge.
Although this requires a bit of a leap to understand, there’s a tool we can use to help us understand these new types of strong charges: an equilateral triangle.
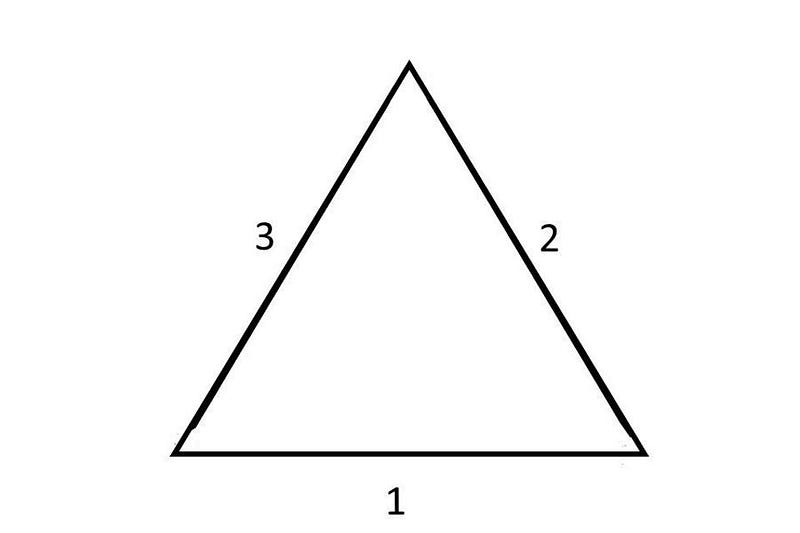
Each “side” of the equilateral triangle, conveniently labeled with “1” on the bottom, “2” on the upper right, and “3” on the upper left, represents a different type of charge that exists under the strong force; every quark has one and only one of these charges assigned to it. Unlike gravity or electromagnetism, however, nature forbids us from having an object that has a net charge under the strong force; only uncharged combinations are allowed.
In electromagnetism, the way we’d arrive at a neutral state is by putting two equal-and-opposite charges together: a positive charge is balanced by a negative charge, and vice versa. With three charges for the strong force, however, there’s a property you might not expect: the way you get something neutral is by creating a combination where there’s an equal number of representatives of all three types of charge together, which is why protons and neutrons contain three quarks apiece.
Each quark, therefore, doesn’t just have this new type of charge inherent to it, but each quark contributes its charge to the overall particle — like a proton or neutron — that contains it. And if you contribute a “1” and a “2” and a “3” together, they bring you back to zero: an overall neutral particle. We can show this, rather than by a triangle’s sides, by each quark leading you in its one particular direction, bringing you back to your starting point only if you wind up with a “neutral” combination.
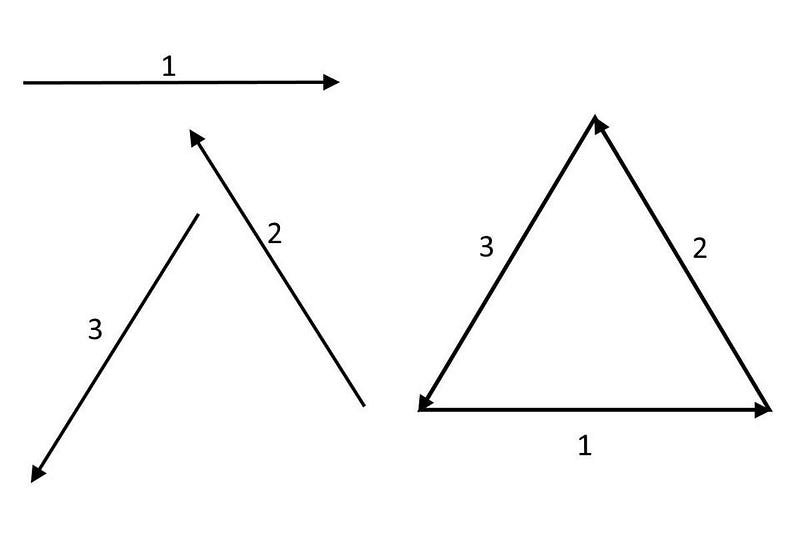
So far, so good. “But wait,” you’re probably thinking, “what about antimatter?” And you’re right: if quarks have three types of positive charges to them, then what about the antiquarks? While normal matter and antimatter are strongly suspected to both have the same types of gravitational charges (positive masses/energies only), all electric charges are reversed for normal matter and antimatter.
So how does it work for the strong force?
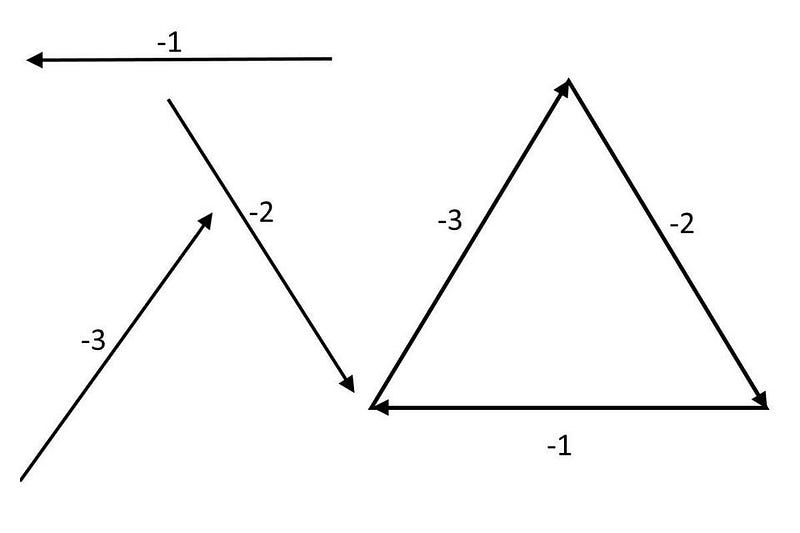
Sure enough: there are “anti-charges” too for each of the antiquarks: the negative equivalents of the “1” and “2” and “3” for normal quarks. You can still think of this as making up a triangle, only this time, “-1” points to the left instead of to the right, “-2” points down and to the right, rather than up and to the left, and “-3” points up and to the left, rather than down and to the right.
The anti-charges for the anti-quarks are equal and opposite to the charges of the quarks they correspond to. Similarly, just as you could put three quarks together to make a proton or a neutron, you can put three antiquarks together to make an antiproton or an antineutron. In fact, all of the known particles called baryons are made of three quarks, and for every baryon, there’s an anti-baryon counterpart made of three antiquarks.
So does that mean that any neutral, uncolored combination is possible in nature?
Although there are other quantum rules that have to be obeyed, the short answer is “yes.” A quark and an antiquark — regardless of whether it’s a “1”/“-1” or a “2”/“-2” or a “3”/“-3” combination — are allowed, corresponding to a meson. Three quarks, a “1” and “2” and “3” together, are allowed, as are three antiquarks: “-1” and “-2” and “-3” all together.
But you can always go up, to more complex combinations.
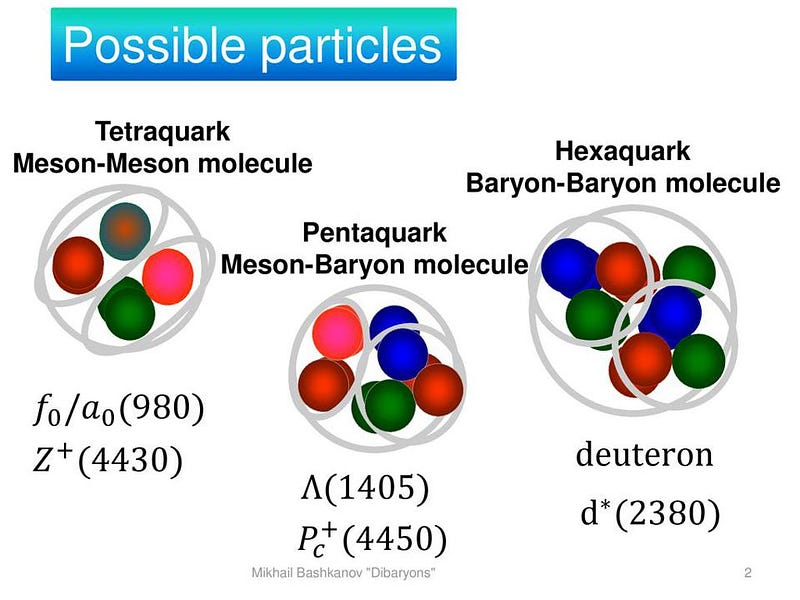
You can have two quarks and two antiquarks bound together: a state known as a tetraquark.
You can have either four quarks and one antiquark, or four antiquarks and one quark, all bound together: a pentaquark.
You can even have six quarks or antiquarks bound together all in a single state, or a three quark-three antiquark combo: either one makes a hexaquark state.
As far as we can tell, every combination imaginable, so long as it doesn’t violate certain other quantum rules that may come into play, is permitted.
Because these charges are just like segments of a triangle that pull you in one direction or another, it’s pretty easy to see that there are many equivalencies at play. For example:
- 1 + 2 + 3 = -1 + 1 = -2 + 2 = -3 +3 = -1 + -2 + -3 = 0 (colorless),
- 2 + 3 = -1, or 1 + 3 = -2, or 1 + 2 = -3 (two quarks can substitute for one antiquark), or
- -1 + -2 = 3, or -2 + -3 = 1, or -1 + -3 = 2 (two antiquarks act as one quark).
Whenever you have a charged particle, it has the potential to interact with any other charged particle. In gravitation, that’s either because of the curvature of spacetime (according to Einstein) or due to the exchange of gravitons (in quantum gravity), which we fully anticipate. In electromagnetism, both like and opposite charges exchange photons. But in this new interaction, the strong interaction, the three different types of charges, plus the three different types of anti-charges, lead to a the exchange of gluons. Instead of one fundamental type, however, there are 8.
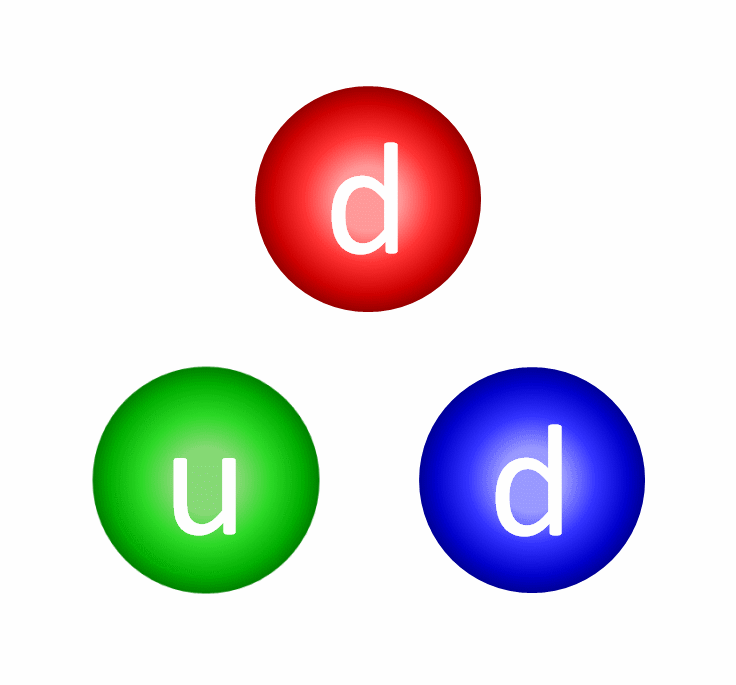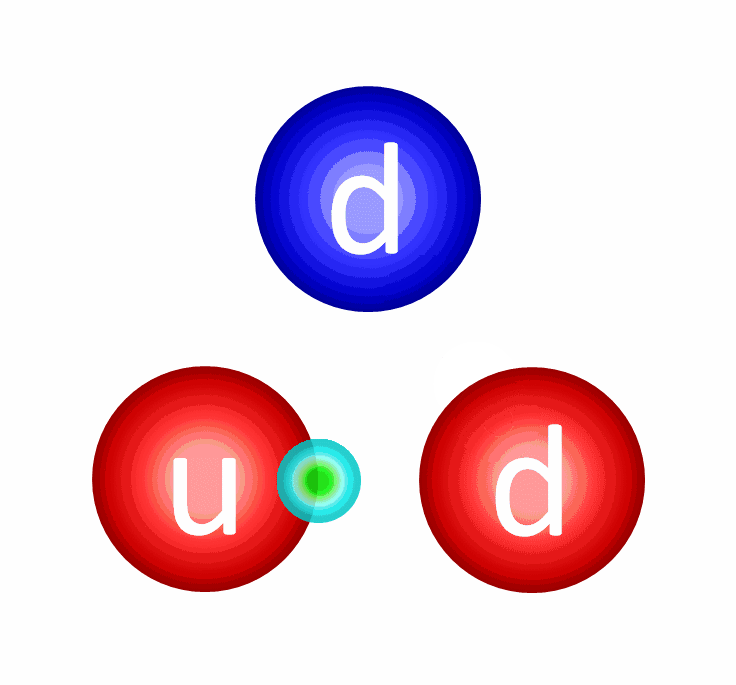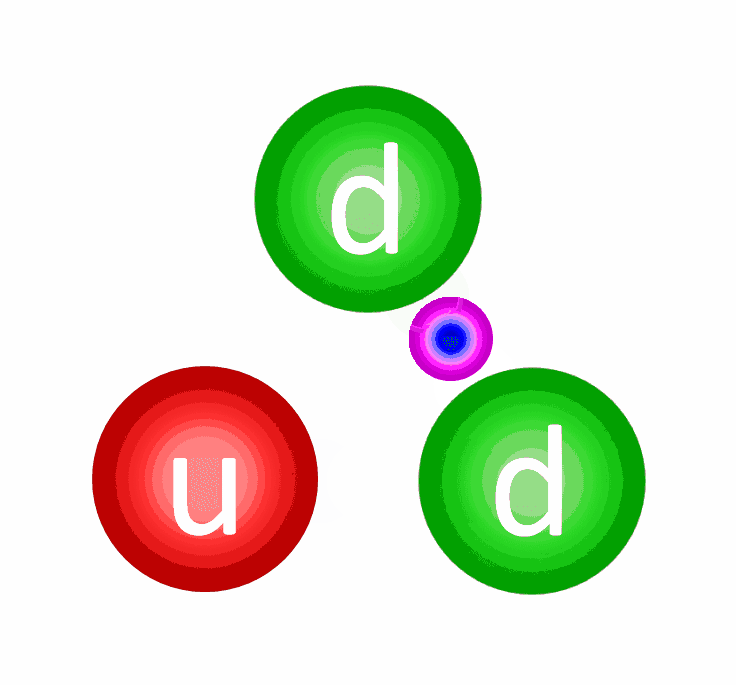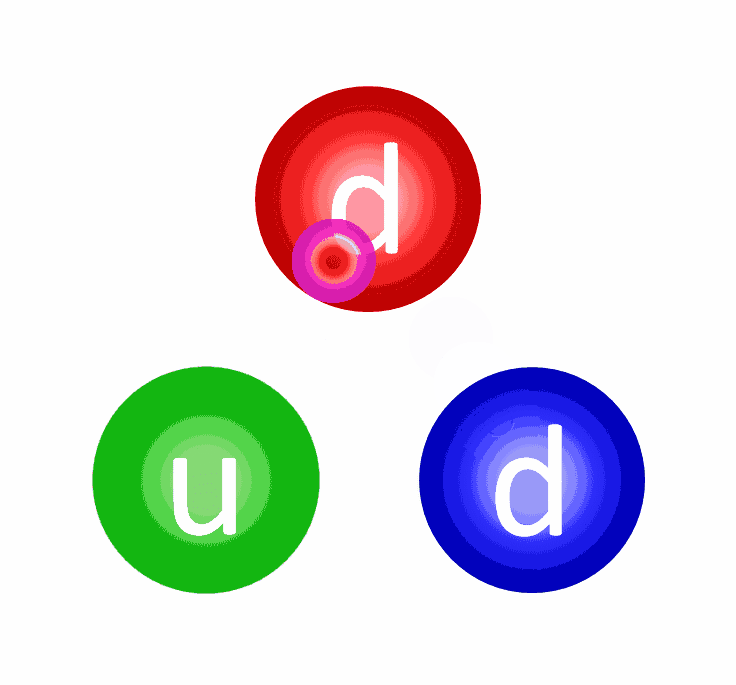
Why eight? Well, every time a charged particle emits a gluon, it has to either stay the same charge or change its charge into one of the other two allowed types. Similarly, every time a charged particle absorbs a gluon, the same thing must occur. The only way this can occur is if every gluon carries with it a combination of a “charge” and an “anti-charge” with it. Six of them are easy. You can have a gluon that’s a combination of:
“1” and “-2”,
“1” and “-3”,
“2” and “-1”,
“2” and “-3”,
“3” and “-1”, or
“3” and “-2”.
But you can’t just pair “1” and “-1” together (or “2” with “-2”, or “3” with “-3”), because quantum mechanically, they’re indistinguishable from one another. Whenever you have indistinguishable quantum states, they mix together. In fact, it gets even more complicated, because these combinations look very similar to the quark-antiquark combinations we briefly mentioned earlier: the mesons.
Because of the way things mix, we get two physical and one unphysical gluon out of the equation, for a total of eight.
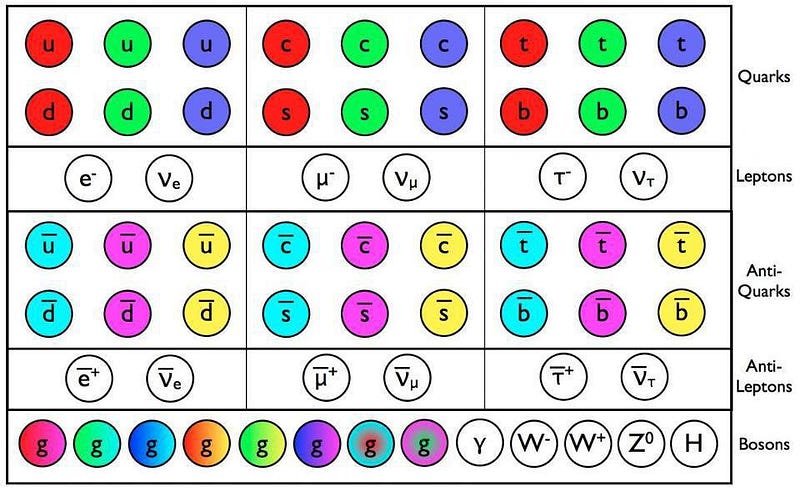
The reason people like the color analogy is because of how similarly color works to this. You can create a colorless combination by either mixing the three primary additive colors (red, green, and blue) together to make white or by mixing the three primary subtractive colors (cyan, magenta, and yellow) together to make black. Red and cyan are anti-colors to one another, as are green and magenta, as are blue and yellow. Just as there are three primary additive and subtractive colors, there are three charges and anti-charges for the strong forces. But the analogy has many fundamental limitations, and it’s important to note that nothing is actually colored at all.
But just as there are two “chargeless” gluons and there are many ways to have a “chargeless” quark-antiquark combination, individual protons and neutrons within a nucleus can attract one another. Gluons (and mesons, for that matter) aren’t just exchanged between individual quarks within a proton or neutron, but can be exchanged between different protons or neutrons within a nucleus.
Remember, as long as you don’t violate any quantum rules, all exchanges are permitted, including exchanges of mesons: all of which are massive particles. Even though the force external to each proton or neutron goes away very quickly at large distances — the fate of all forces mediated by massive particles — this interaction, known as the residual strong force, is what winds up practically preventing all atomic nuclei from spontaneously splitting back into free protons and neutrons.
It’s true that the Universe obeys arcane and complicated rules, and that the best language for expressing those rules happens to be mathematics. But that doesn’t mean we shouldn’t endeavor to be translators, keeping the accuracy of the rules but making them accessible to far greater numbers of people. Every time we learn of a new way to present a scientific or mathematical phenomena, we gain a new tool in our arsenal for not only teaching it to others, but for better understanding it ourselves.
The strong interaction obeys all of the group theory rules associated with the special unitary group SU(3), but unless you’re an advanced graduate student in either physics or math, that’s probably not a language you speak. It can be described in terms of color, but the flaws in that analogy often leave long-lasting misconceptions even among physicists. The “triangle” analogy is more uncommon, but might help keep more of the mathematical intricacy of the theory while simultaneously eliminating numerous points of colorful confusion. However you slice it, there’s an entirely new set of nuclear forces at play inside atomic nuclei, and the strong force is what holds every nucleus in the Universe together. The better we understand it, the better we understand the physics at the literal core of our very existence.
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.





