There are no free quarks

Other particles — electrons, neutrinos, photons and more — can exist on their own. But quarks never will. Here’s why.

Image credit: Wikimedia Commons user Maschen under C.C.-1.0.

“In physics, you don’t have to go around making trouble for yourself — nature does it for you.” –Frank Wilczek

Earlier this week, the 2014 Nobel Prize in Physics was awarded for the developments that led to the invention of the blue LED. But ten years prior, in 2004, it went to a trio of physicists who explained the most bizarre force we’ve ever come to understand: the strong force. Sure, it holds individual protons and neutrons together, it allows nuclei to bind together, it explains fusion and fission, and it accounts for more than half of the particles and interactions in the Standard Model.

But it’s also the weirdest force we’ve ever encountered. Let me explain, and let’s do it by starting with what you think of as the “simplest” force of all: gravity.

It’s pretty straightforward, isn’t it? Everything in the Universe has some amount of mass or energy (or both) as a property of itself, and it exerts an force on everything else with a mass or energy, too. Whether you think about it as Newton did or as Einstein did, the same general picture holds.

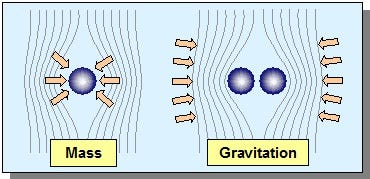
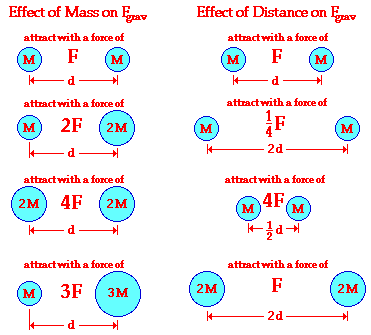
Rather than think about mass or energy, we can think about both of those combined (via E = mc^2, if we like) as a gravitational charge. There’s only one type of charge — a positive one — and there’s only one type of force: an attractive one. All gravitationally charged bodies (anything with mass, for example) attract all other gravitationally charged bodies, and the force gets larger if either the charge gets bigger or the objects get closer. In the particular case of gravity, an object with double the mass experiences double the force, and an object that’s only half the distance away experiences quadruple the force. (Ignoring relativistic effects.) If you take your gravitationally charged objects and move them arbitrarily far away, the force between them drops to zero. This last part is incredibly important, and you should remember it (so I’ll say it again in a larger font):

As the distance between two gravitationally objects gets larger and larger, the gravitational force drops to zero.

So that’s gravity: arbitrarily weak at large distances, where everything (that’s outside a black hole’s event horizon) can become free with enough energy.

When we come to electromagnetism, that force is suddenly a little more complicated. Sure, it’s like gravity in a way: get yourself a positive and a negative charge and they’ll attract one another the same way two masses do. They’ll even do it in almost the same fashion: double the charge on one and the force between them doubles, halve the distance between them and the force quadruples.

But there are two different types of charges here: positive and negative.

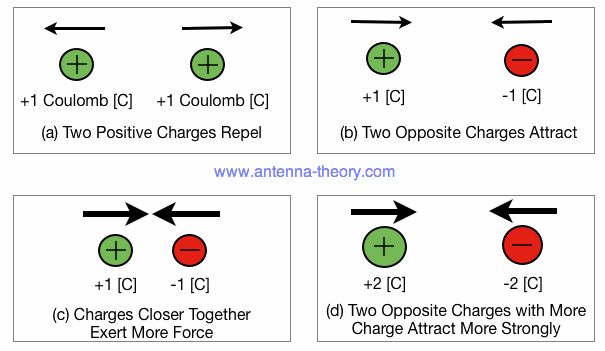
The like charges (positive-positive and negative-negative) repel one another while the opposite charges (positive-negative and negative-positive) attract. This is a pretty big difference, because now things can actually be driven apart, not only together. But the form of the force law — the fact that the force is greater at smaller distances — is still the same as it is for gravitation. We have two type of charge (positive and negative), but the force still drops to zero at large distances.

These two forces — gravitation and electromagnetism — are the two most common types of forces, and hence the two forces that are in line with our intuition. But then we get to the strong force, and everything changes.

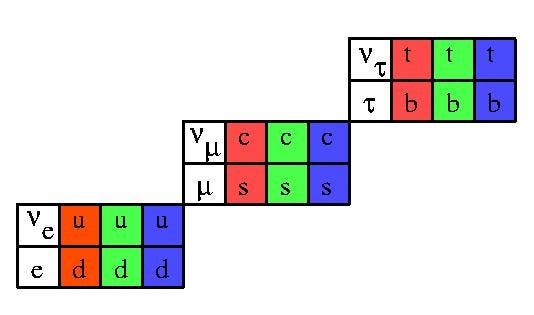
First off, there’s no longer one type of charge, nor even two, but three. Instead of mass (gravitational charge), which is always positive and always attractive, or electric charges, which can be positive or negative and either attractive or repulsive depending on their combination, all of the quarks come with one of three types of charge attached to them: red, green or blue.

Second off, these aren’t fixed properties of the quarks! If you give me a particle (e.g., an electron) with a mass, that mass is a property intrinsic to that particle. If you give me a particle with an electric charge (say, an electron again), that electric charge is a property of the particle itself: it doesn’t change. But if I gave you a quark — say, a red up quark — it would remain an up quark with a charge of +(2/3)e, and with an intrinsic mass of around 2.3 MeV/c^2, but that “red” property it had is transient! When you look at it a fraction of a second later, it might be blue or green, depending on what interactions its undergone!

And third, the strong force is always attractive, but not in the same way that either gravitation or electromagnetism behaves. This is a little more nuanced, so we’ll come back to this one.

Let’s start by showing you how “color” works inside, say, a single neutron.

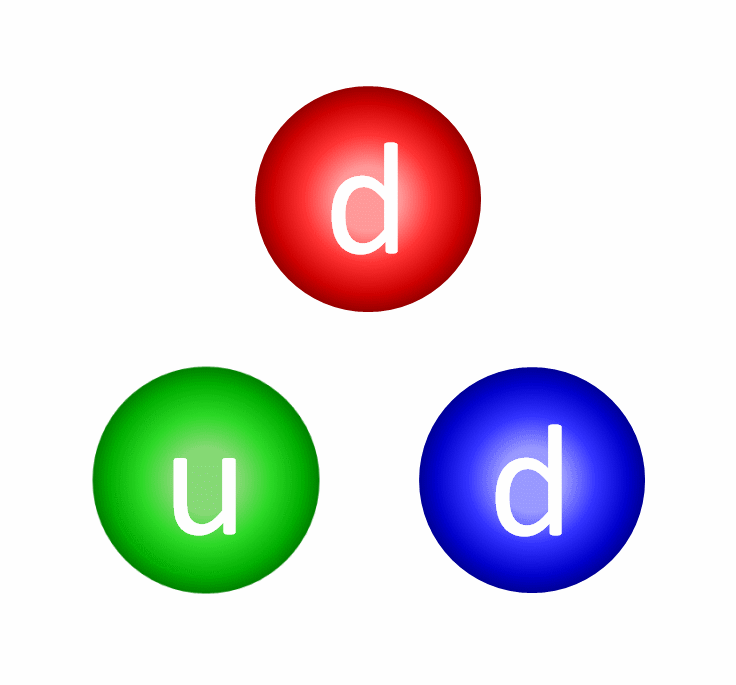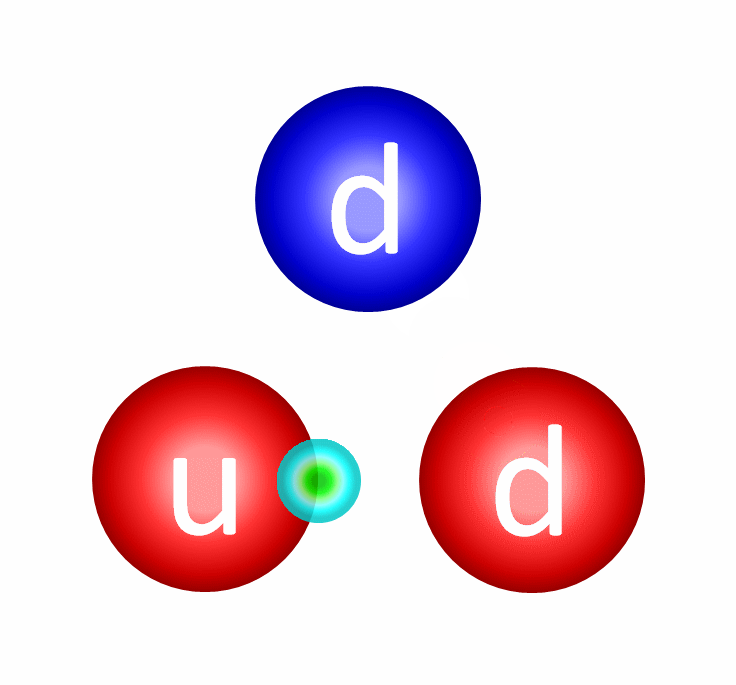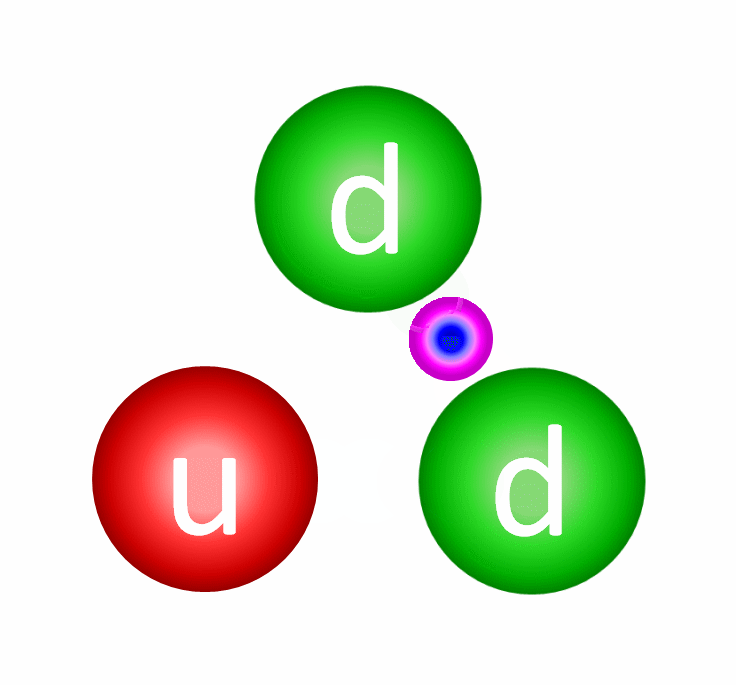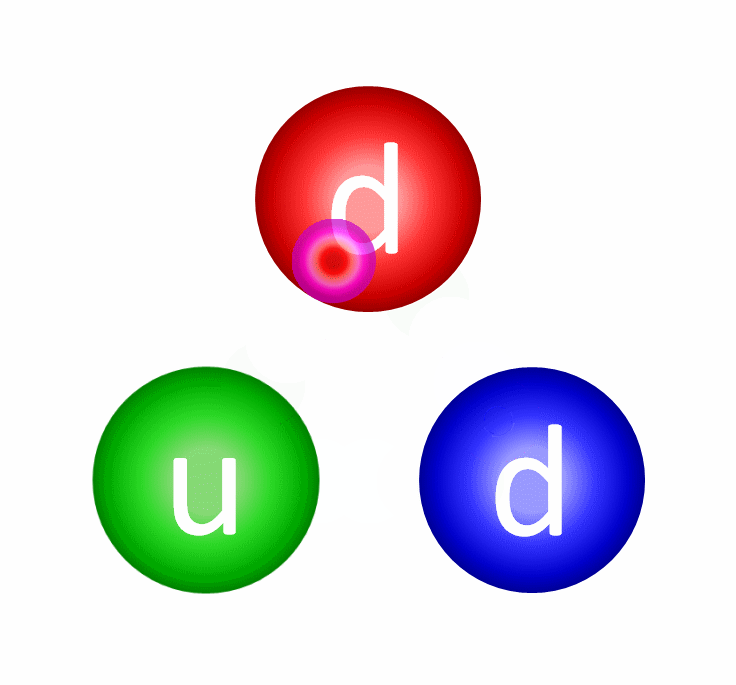
With one up quark and two down quarks, you might think there are a whole slew of different color combinations that could be present here. For your three quarks, maybe you have two reds and a blue, two blues and a green, or maybe three greens? But you don’t: at any given time, you always have one red, one green and one blue. The individual colors can either change or stay the same through the exchange of gluons, and there are eight gluons total which have a color-anticolor combination. This is already weird! In gravitation, we had only one type of charge: positive and attractive. In electromagnetism, we had two types: positive and negative (where negative is “anti-positive”), which could be attractive or repulsive in combinations. But now for colors, we have three types, and each type has its own anti-type!

But these types and anti-types are all related in a very strange way.

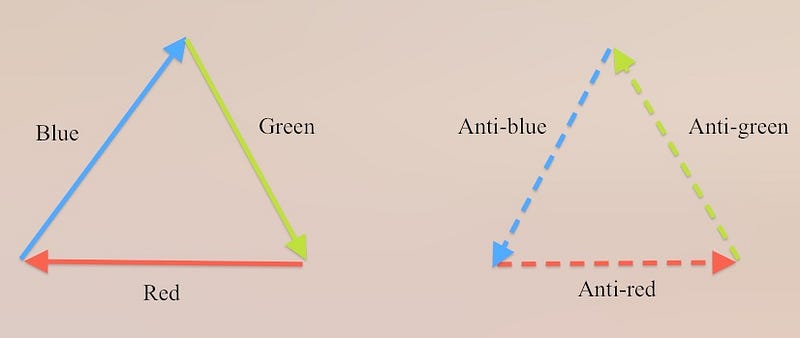
You see, I like to think of red, green and blue colors as three “directions” that make up the sides of an equilateral triangle. If you want something to be stable, it can’t have a net color, so you have to have some type of combination that takes you back to your starting point. So you can have three quarks, three antiquarks, a quark-antiquark combination, or some combination of the previous three. (For example, four quarks and an antiquark, two quarks-two antiquarks, six antiquarks, etc.) This is a little bit weird, because even though there are three colors and three anti-colors, they’re all related, and give us a few different ways to get to “colorless,” or what we simply call white.

So that explains why we only see things like protons and neutrons (which are examples of baryons, or three-quark combinations), antiprotons and antineutrons (anti-baryons, with three antiquarks each), or particles like pions and kaons (which are mesons, or quark-antiquark combinations): you have to wind up colorless.

But what if you just took, say, a pi-meson, which can be a combination of an up quark and an anti-down antiquark, and tried to rip that quark-antiquark combination apart? Could you?

You can try, but the more energy you put in to the system to get these two colored entities farther apart, the stronger and stronger the attractive force would get. It’s kind of like a spring: the farther and farther you stretch it, the greater the force with which it wants to “snap” back.

But if you insist on pulling them farther and farther apart, you’ll eventually require so much energy that you’ll simply create new particle-antiparticle pair out of empty space!

There’s an important reason for this that’s very different from our other forces. In gravity, if you have a single mass (gravitational charge) all by itself, the force it generates is strong close to it, but drops to zero as you move away. In electromagnetism, if you have a single charge (electric charge) all by itself, same deal: the force it generates (either attractive or repulsive) is strong very close to it, but drops to zero as you move away.

But in the strong force, if you have a single color charge all by itself, the force it generates gets stronger and stronger the farther you are away from it, and only drops to zero when you’re very close! If you ever had a free quark, even temporarily, even if it was only “free” for a very small distance around it, it would require a huge amount of energy to create, and it would immediately begin pulling particle-antiparticle pairs out of the vacuum until everything was colorless again.

If this sounds crazy, that’s probably because it is, but it’s the only way to explain what nature does when we take, say, two protons and smash them together at incredibly high energies.

Every once in a while, we’ll see a huge “jet” of particles (usually two, sometimes three or four) that fly off from the high-energy collision point. How do you get so many baryons, antibaryons and mesons together in one place? Because for a very brief moment, you created a quark (or antiquark) that was “too free,” and it began to pull all these particle-antiparticle pairs out of the quantum vacuum until everything was color-neutral once again!

And it’s that weirdness — that the force and energy required to “free” a quark rises exponentially as its distance from other quarks rises — that won the 2004 Nobel Prize in Physics. This new idea, that the force would go to zero at short distances but rise rapidly at large ones, is known as asymptotic freedom, and explains why nuclei are bound together into small but finite sizes, and it’s this binding force that’s responsible for some 99% of the mass of protons and neutrons!

So you’ll never have a free quark that lasts in the Universe, as the energy required to “free” it is more than enough to create new particles that will cause it to spontaneously re-confine itself into a colorless state. And despite how counterintuitive it is, now you know why!

Leave your comments at the Starts With A Bang forum on Scienceblogs!