This 90-year-old math problem shows why we need quantum computers

It’s time to run your errands, and you’ve got multiple stops to make. From your house, you have to hit the supermarket, the gas station, and the hardware store, all before returning home. Assuming you know that you begin and end at your home, there are six possible routes you can take, as you can either hit:
- first the supermarket, next the gas station, and then the hardware store,
- first the supermarket, next the hardware store, and then the gas station,
- first the gas station, next the supermarket, and then the hardware store,
- first the gas station, next the hardware store, and then the supermarket,
- first the hardware store, next the supermarket, and then the gas station, or
- first the hardware store, next the gas station, and then the supermarket.
But which one of these routes will be the most efficient path? This is known, in the field of mathematics, as the traveling salesman problem. To solve it for more than a handful of “stops,” it will almost certainly require a quantum computer. Here’s why.
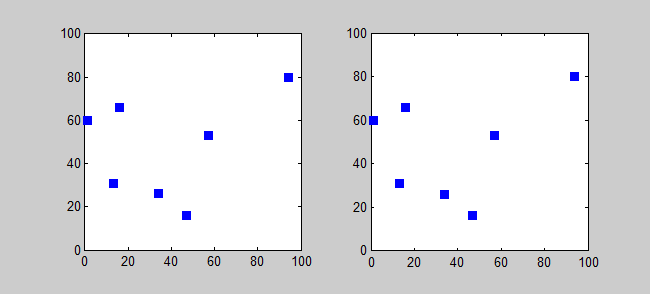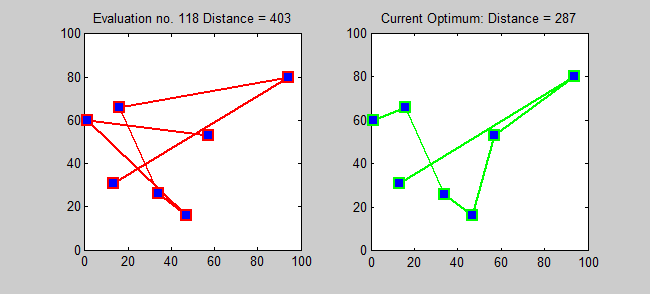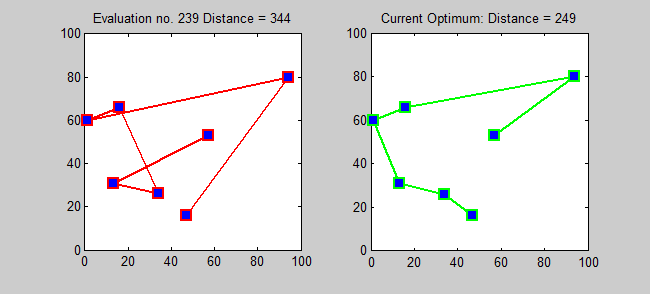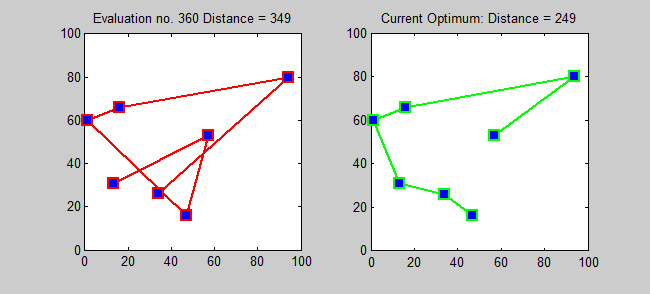
If you have any number of destinations that you have to visit, there will be one travel route that’s more efficient than all the rest: that wastes the least amount of time and distance travelling between them. The above example — about your home, the supermarket, the gas station, and the hardware store — had a total of four destinations, but only six possible paths. As it turns out, only three of those paths are unique, because each option (e.g., home ⇨ supermarket ⇨ gas station ⇨ hardware store ⇨ home) is one of the other options in reverse (e.g., home ⇨ hardware store ⇨ gas station ⇨ supermarket ⇨ home).
This is pretty straightforward for only a few stops, but the number of possible paths grows extremely rapidly: like a mathematical factorial. For 5 destinations, there are 12 possible unique paths; for 10 destinations, there are 181,400 unique paths; for 15 destinations, there are over 43 billion unique paths.
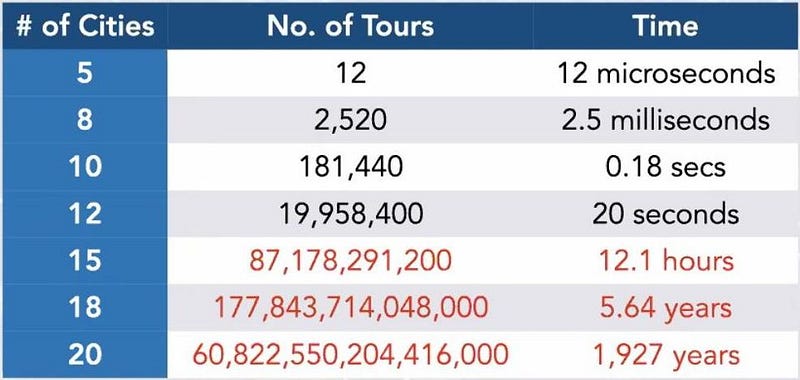
The simplest approach to solving this type of problem is to use what we call “brute force.” The brute force approach would simply take possible way to travel between however many destinations you had, calculate the distance of that path, and to determine which one was the shortest. The problem is that the number of possible outcomes — or the number of “tours” for the travelling salesman — rises incredibly quickly.
For any number of total destinations, call it N, the number of possible tours is (N-1)!/2. If you only had 5 destinations, it wouldn’t take that long to calculate the distances for all 12 possible tours; a typical modern computer takes about a microsecond to calculate one tour. But if you went up to 10 destinations, it would take almost a full second. At 15 destinations, it takes about half a day, and for 20 destinations, it would take about 2,000 years. By the time you reach 25 destinations, you’d have to run your computer for about 10 billion years to optimize your path: about as long as the age of the Universe.

This problem — like many problems one can formulate — belongs to a class of problems that are classified as computationally expensive. To find the optimal solution among a myriad of possible combinations requires examining every reasonable path that one could imagine taking, quantifying the distance (or time) requires for that path, and then choosing the shortest (or fastest) one.
In practice, the brute force approach isn’t the only one, and superior methods for finding exact solutions (largely by ruling out “obviously non-optimal” paths) exist, similar to advances made in computer chess. The largest exact solution was achieved in 2006, when the shortest path through 85,900 cities was found. It took over a century’s worth of CPU-years to find that solution.
This type of problem, despite its simplicity, actually has a large number of practical applications. (And no, not only for people named Santa Claus.) If you have a series of packages going to a series of addresses, you’ll want to take the optimal route. If you’re planning out your travelling route, from errand trips to road trips, you won’t want to waste time or mileage. And if you’re in the airline industry, the manufacturing industry, or the transportation industry, you’ll want to get your passengers and cargo to their destination as quickly and efficiently as possible.
But if your problem is too complex — if you have too many destinations, for example — you’ll only ever be able to come up with approximate solutions; you cannot be certain that you found the best route, or even one of the best routes. The solution you arrive at will be limited by your computational power and the quality of your algorithm. Some problems, quite simply, are hard to solve with classical computers.
Fortunately, many computationally difficult problems — including, quite possibly, some aspects of the travelling salesman problem — are far less difficult (and far less computationally expensive) using a quantum computer. It was proven, just a few years ago, that quantum computers possess a computational advantage over anything a classical computer could ever achieve.
When quantum supremacy was achieved for the first time in 2019 (albeit only for a specific problem), it was a stunning example of how quantum computers could practically solve problems faster and more efficiently than conventional, classical computers ever could. While it’s always possible that new algorithms or methods could lead to a faster solution for any particular problem on a classical computer, quantum computers maintain some fundamental advantages.
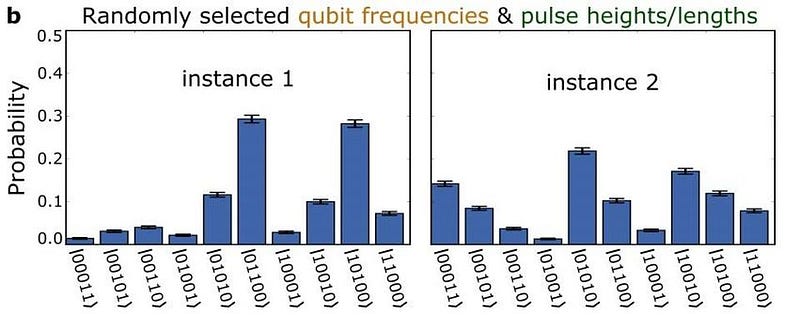
Instead of bits that must be either 0 or 1, they work with indeterminate qubit states that exist in superpositions of 0 and 1 simultaneously. Moreover, you can also perform quantum operations (rather than just the classical ones) on these qubits directly, maintaining all of that quantum weirdness (including indeterminism) all the way up through the very end of the computation.
This is where the true power of quantum computing lies: in taking advantage of the fact that some problems can be solved efficiently using a quantum computer, but classical computers can only solve them inefficiently. This was proven in 2018 by computer scientists Ran Raz and Avishay Tal, who demonstrated that quantum computers can efficiently solve problems that:
- are not quickly solvable by a classical computer,
- cannot have their solutions quickly checked by a classical computer,
- and do not fall into the generalized category of all problems that classical computers could theoretically solve in polynomial time.

This brings us back to the travelling salesman problem. It’s not a problem that’s quickly solvable by a classical computer, even with the best algorithms ever devised. If you were given a specific distance, you could easily check whether any path that you found is shorter than that distance or not, but there’s no guarantee that’s the shortest distance of all.
But really, that’s what you want to know: is the shortest possible path exactly equal to the specific distance covered by the shortest path you’ve found?
Perhaps someday, even if it hasn’t happened in all the time this problem has been examined, we’ll be able to discover an algorithm for a classical computer that can efficiently find that solution. It’s not guaranteed that such an algorithm exists, but the quest to discover one remains the hope of many.

Irrespective of whether that specific problem — or the generalization of all such theoretical problems — eventually yields to a classical computer or not, however, there will still remain problems that go beyond the limits of what a classical computer could ever efficiently do. There are problems that we can pose that have a “yes” or “no” answer, but that aren’t solvable in polynomial time by a classical computer, even theoretically.
However, at least some of those problems, even the ones that cannot be efficiently solved by a classical computer, can be efficiently solved by a quantum computer. Although we do not know if the traveling salesman problem will ever be efficiently solvable by a classical computer, we do know that there are categories of problems that quantum computers can efficiently solve that classical ones cannot. If a classical solution exists, then a quantum one does too; but even if a classical solution doesn’t exist, a quantum one may yet be possible.

Finding the most efficient route between a large number of nodes — the essence of the travelling salesman problem — has a myriad of practical applications. It shows up in DNA sequencing. It appears in the planning and manufacture of microchips. It rears its head in planning observing runs of many objects in astronomy. And it’s essential in optimizing delivery routes and supply-chain logistics. But for all its importance and relevance in human society, we do not yet know how to solve the problem efficiently: in what computer scientists call polynomial time.
Even if no such solution exists, and it might not with a classical computer, the world of quantum computers offers unparalleled hope. A quantum computer can solve classes of problems that no classical computer can efficiently solve, and perhaps that will someday include the travelling salesman problem. When your brute force options are too expensive and an efficient algorithm eludes you, don’t give up on ever solving the problem altogether. The quantum computing revolution might yet make it possible.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.





