This Is How, 100 Years Ago, A Solar Eclipse Proved Einstein Right And Newton Wrong

The solar eclipse of May 29, 1919, was the nail in the coffin of a Newtonian Universe.
On May 29, 1919, the world changed forever. For hundreds of years, Isaac Newton’s theory of gravity — the law of universal gravitation — had gone unchallenged, as its predictions matched every observation or measurement that had ever been made. But a mismatch between Newton’s predictions for the orbit of Mercury and what astronomers saw surfaced in the mid-19th century, and scientists struggled to explain it.
Perhaps we needed to modify the laws of gravity, after all. Evidence mounted when special relativity came out, demonstrating that there was no such thing as absolute distance. Newton’s theory predicted an instantaneous force, again violating relativity. In 1915, Albert Einstein put forth a new alternative theory of gravity: General Relativity. The way to test it against Newton’s theory was to wait for a total solar eclipse. 100 years ago today, Einstein was proven right. Here’s how.

Today, Albert Einstein’s General theory of Relativity is arguable the most successful theory of all-time. It explains everything from GPS signals to gravitational redshift, from gravitational lensing to merging black holes, and from the timing of pulsars to the orbit of Mercury. The predictions of General Relativity have never once failed.
When this theory was first introduced in 1915, it was attempting to replace Newton’s gravitation. Although it could reproduce the earlier Newtonian successes and explain the orbit of Mercury (where Newton could not), the most critical test would come in the form of a new prediction that severely differed from the predictions of the universal law of gravitation. A total solar eclipse would provide a unique and straightforward opportunity.
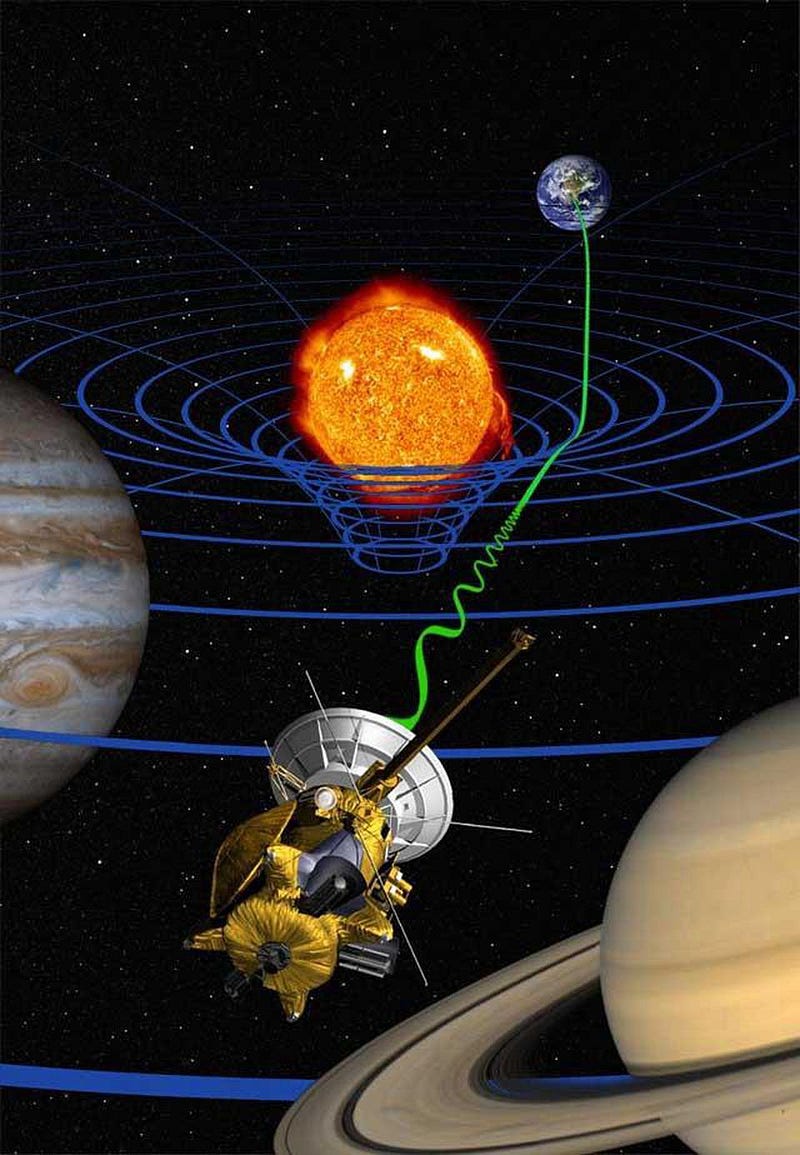
In Newton’s gravity, anything with mass attracts anything else with mass. Even though light is massless, it has an energy, and therefore you can assign an effective mass to it through Einstein’s E = mc². (You find that m = E/c².) If you allow a photon to pass near a large mass, you can use this effective mass to predict how much the starlight should bend by, and you get a specific value. Near the limb of the Sun, it’s just under 1″ (arc-second), or 1/3600th of 1°.
But in Einstein’s General Relativity, both space and time are distorted by the presence of mass, whereas in Newton’s gravity, only an object’s motion through space is affected by the gravitational force. This means that Einstein’s theory predicts an extra factor of 2 (actually slightly more, especially as you get closer to the mass in question) over Newton’s, or a deflection near the Sun of closer to 2″.
The history of how Einstein’s General Relativity came to be is fascinating, because it’s only the fact that Newton’s gravitation eventually had problems that motivated Einstein to formulate his new concept.
Newtonian gravity, put forth in 1687, is an extraordinarily simple law: put any masses anywhere in the Universe, a fixed distance apart, and you immediately know the gravitational force between them. This explained everything from the terrestrial motion of cannonballs to the celestial motion of comets, planets, and stars. After 200 years, it had passed every single test that was thrown its way. But one pesky observation threatened to derail everything: the detailed motion of the innermost planet in our Solar System.
Every planet moves in an ellipse around the Sun. However, this ellipse isn’t static, returning to the same fixed point in space with every orbit, but rather, it precesses. Precession is like watching that ellipse rotate in space over time, albeit very slowly. Mercury had been observed with incredible precision since Tycho Brahe in the late 1500s, so with 300 years of data, our measurements were extraordinary.
According to Newton’s theory, its orbit should have precessed by 5,557″-per-century, due to the precession of Earth’s equinoxes and the gravitational effects of all the planets on Mercury’s orbit. But observationally, we observed 5,600″-per-century instead. That difference, of 43″-per-century (or just 0.00012°-per-year), had no explanation in Newton’s framework. Either there was an extra planet interior to Mercury (which observations ruled out), or something was wrong with our old theory of gravity.
But Einstein’s new theory could explain the mismatch. He spent years developing the framework for General Relativity, where gravitation wasn’t caused by masses attracting other masses, but rather by matter and energy curving the very fabric of space, which all objects then move through. When gravitational fields are weak, Newton’s law is a very good approximation to what Einstein’s theory laid down.
Close to very large masses or at high speeds, however, Einstein’s predictions differed from Newton’s, predicting exactly that 43″-per-century difference. But the bar to overthrow a scientific theory is higher than that. To supersede the old theory, a new one must do the following:
- Reproduce all the successes that the old theory enjoyed (otherwise, the old theory is still superior in some way),
- Succeed in the regime where the old theory could not (otherwise, your new theory doesn’t fix the problem with the old one),
- And to make a new prediction that you can go out and test, distinguishing between the old-and-new ideas (otherwise, you don’t have any scientifically predictive power).
That last piece is where the solar eclipse comes in.
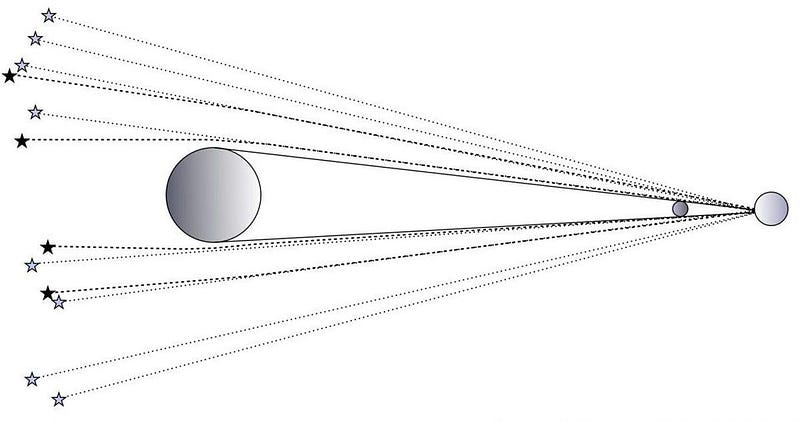
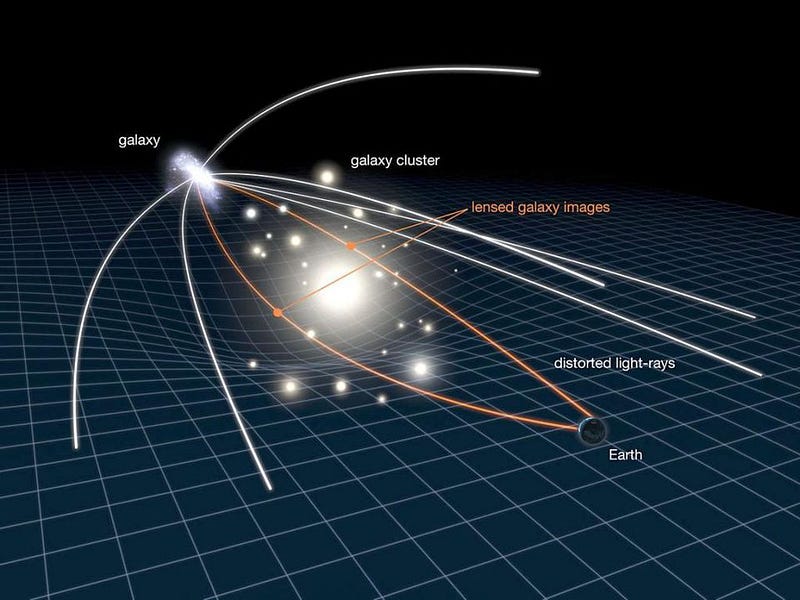
When the stars appear in the night sky, the starlight travels to our eyes from a different location in the galaxy, many light years away. If Newton was correct, that light should either travel in a completely straight line, undeflected by any masses it passes near (since light is massless), or that it should bend due to the gravitational effects of mass-energy equivalence. (After all, if E = mc², then perhaps you can treat light as have an effective mass of m = E/c².)
But Einstein’s theory, particularly if light passes very close by a large mass, offers a prediction different from both of these numbers. That extra factor of 2 (or, rather, 2 and an extra few parts-per-million) is a unique and very specific prediction from Einstein’s theory, and one that could be tested by making two observations at different times of the year.
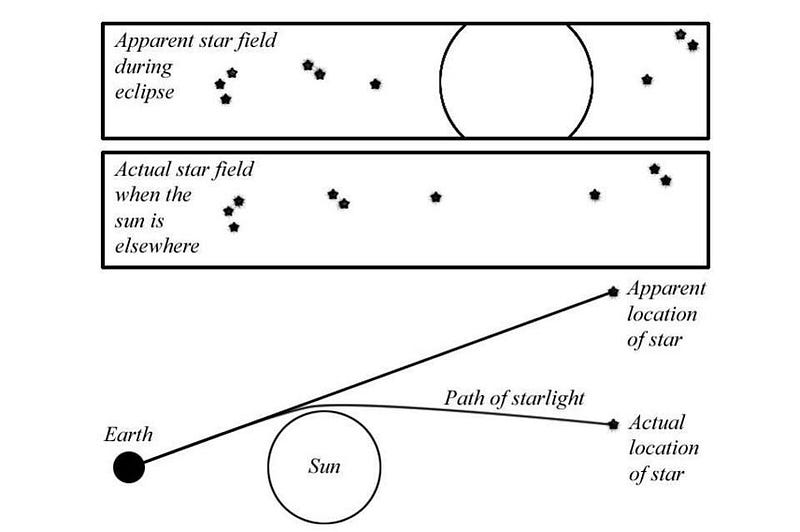
The largest mass we have close by Earth is the Sun, which normally renders starlight invisible during the day. As starlight passes near the edge of the Sun, according to Einstein, it should travel along that curved space, causing the light-path to appear bent. During a total solar eclipse, however, the Moon passes in front of the Sun, blocking its light and causing the sky to become as dark as night, enabling the stars to be seen during the daytime.
If you previously measured those stellar positions to an accurate enough precision, you could see whether they’ve shifted or not — and by how much — due to the presence of that large, nearby mass. If you could detect a deflected position at the sub-arc-second level, you could know definitively whether Newton’s, Einstein’s, or neither prediction was correct.
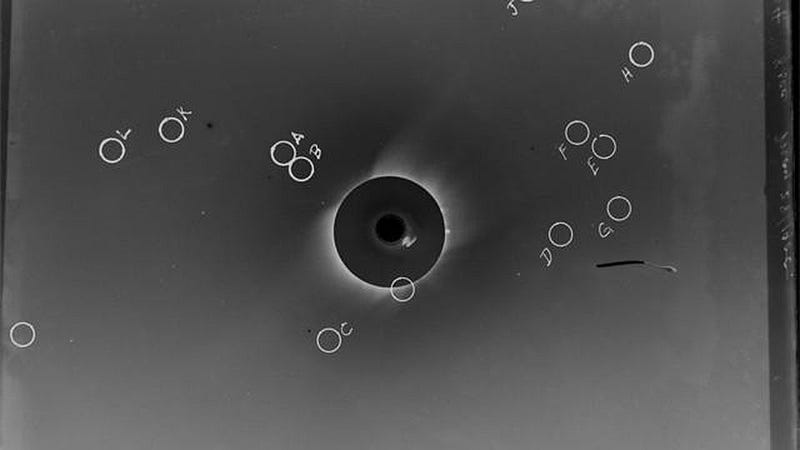
Photographic plates of the Sun during a total solar eclipse had revealed not only details in the Sun’s corona before, but the presence and positions of stars during the daytime. However, none of the pre-existing photographs were high enough in quality to determine the deflected positions of nearby stars to the necessary accuracies; the deflection of starlight is a very small effect requiring very precise measurements to detect!
After Einstein set forth his general theory of relativity in 1915, there were a few chances to test it: 1916, which World War I interfered with, 1918, where attempted observations were defeated by clouds, and 1919, which is where the first successful test took place. Arthur Eddington masterminded an expedition that involved two teams, one in Brazil and one in Africa, to photograph and measure these stellar positions during one of the 20th century’s longest total eclipses: nearly 7 minutes in duration.
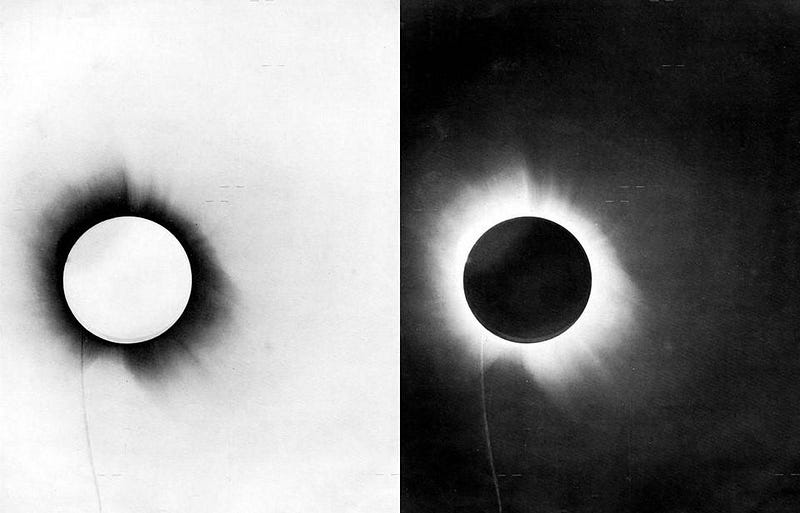
The results of those observations was compelling and profound: Einstein’s theory was right, while Newton’s broke down in the face of the bending of starlight by the Sun. Although the data and analysis was controversial, as many accused (and some still accuse) Arthur Eddington of “cooking the books” to get a result that confirmed Einstein’s predictions, subsequent eclipses have shown definitively that General Relativity works where Newton’s gravity does not.
In addition, careful reanalysis of Eddington’s work shows that it was, in fact, good enough to confirm the predictions of General Relativity. The features in newspapers around the world trumpeted this tremendous success, and even a century later, some of the world’s best science writers are still publishing wonderful books on this remarkable achievement.

Today, May 29, 2019, marks the 100th anniversary of the day, the event, and the expedition that validated Einstein’s General Relativity as humanity’s leading theory of how gravitation works. Newton’s laws are still incredibly useful, but only as an approximation to Einstein’s theory with a limited range of validity.
General Relativity, meanwhile, has gone on to successfully predict everything from frame-dragging to gravitational waves, and still has yet to encounter an observation that conflicts with its predictions. Today marks a full century of General Relativity’s demonstrated validity, with not even a hint of how it might someday break down. Although we certainly don’t know everything about the Universe, including what a quantum theory of gravity might actually be like, today is a day for celebrating what we do know. 100 years after our first critical test, our best theory of gravity still shows no signs of slowing down.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.