This Is Why Quantum Field Theory Is More Fundamental Than Quantum Mechanics

And why Einstein’s quest for unification was doomed from the start.
If you wanted to answer the question of what’s truly fundamental in this Universe, you’d need to investigate matter and energy on the smallest possible scales. If you attempted to split particles apart into smaller and smaller constituents, you’d start to notice some extremely funny things once you went smaller than distances of a few nanometers, where the classical rules of physics still apply.
On even smaller scales, reality starts behaving in strange, counterintuitive ways. We can no longer describe reality as being made of individual particles with well-defined properties like position and momentum. Instead, we enter the realm of the quantum: where fundamental indeterminism rules, and we need an entirely new description of how nature works. But even quantum mechanics itself has its failures here. They doomed Einstein’s greatest dream — of a complete, deterministic description of reality — right from the start. Here’s why.
If we lived in an entirely classical, non-quantum Universe, making sense of things would be easy. As we divided matter into smaller and smaller chunks, we would never reach a limit. There would be no fundamental, indivisible building blocks of the Universe. Instead, our cosmos would be made of continuous material, where if we build a proverbial sharper knife, we’d always be able to cut something into smaller and smaller chunks.
That dream went the way of the dinosaurs in the early 20th century. Experiments by Planck, Einstein, Rutherford and others showed that matter and energy could not be made of a continuous substance, but rather was divisible into discrete chunks, known as quanta today. The original idea of quantum theory had too much experimental support: the Universe was not fundamentally classical after all.
For perhaps the first three decades of the 20th century, physicists struggled to develop and understand the nature of the Universe on these small, puzzling scales. New rules were needed, and to describe them, new and counterintuitive equations and descriptions. The idea of an objective reality went out the window, replaced with notions like:
- probability distributions rather than predictable outcomes,
- wavefunctions rather than positions and momenta,
- Heisenberg uncertainty relations rather than individual properties.
The particles describing reality could no longer be described solely as particle-like. Instead, they had elements of both waves and particles, and behaved according to a novel set of rules.
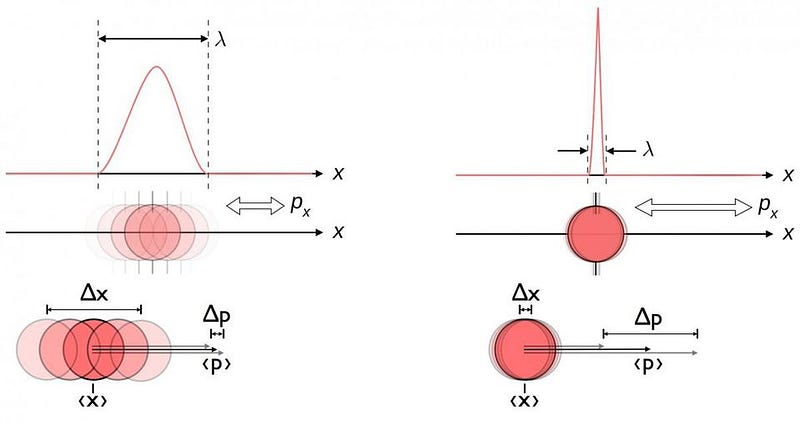
Initially, these descriptions troubled physicists a great deal. These troubles didn’t simply arise because of the philosophical difficulties associated with accepting a non-deterministic Universe or an altered definition of reality, although certainly many were bothered by those aspects.
Instead, the difficulties were more robust. The theory of special relativity was well-understood, and yet quantum mechanics, as originally developed, only worked for non-relativistic systems. By transforming quantities such as position and momentum from physical properties into quantum mechanical operators — a specific class of mathematical function — these bizarre aspects of reality could be incorporated into our equations.
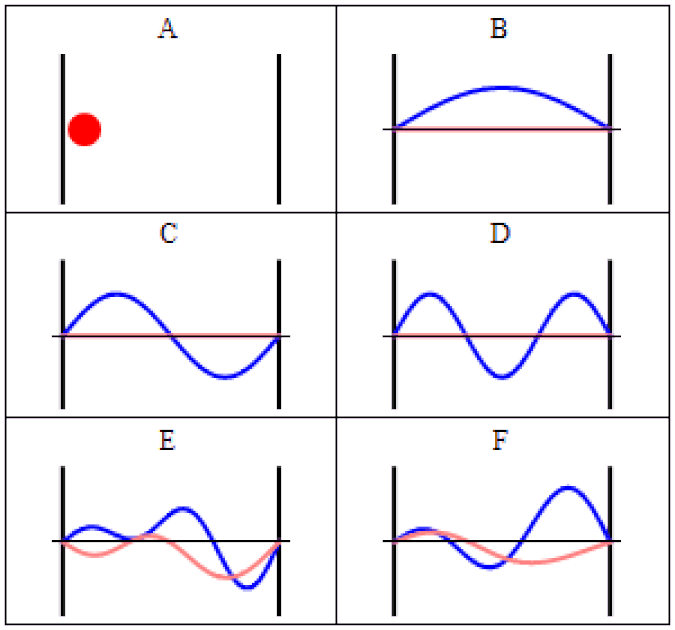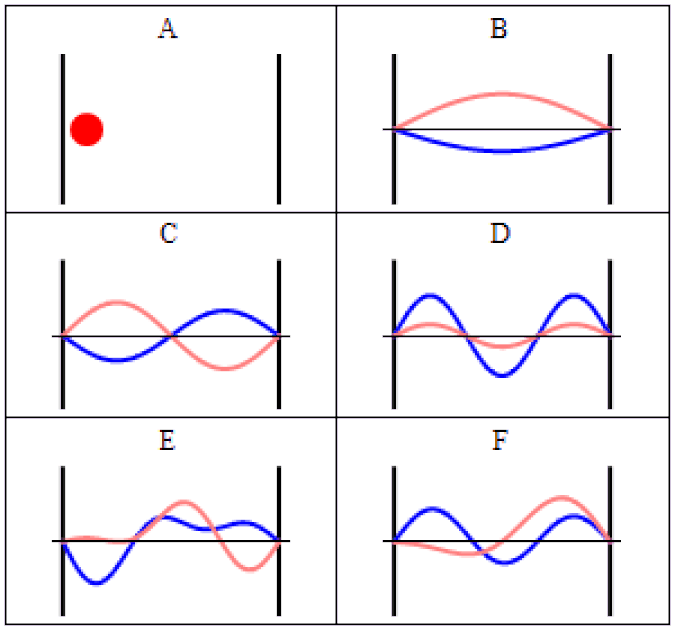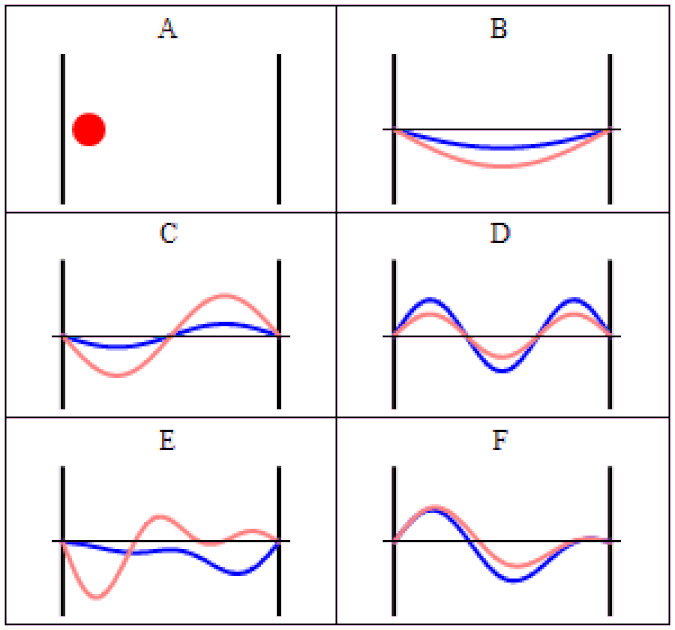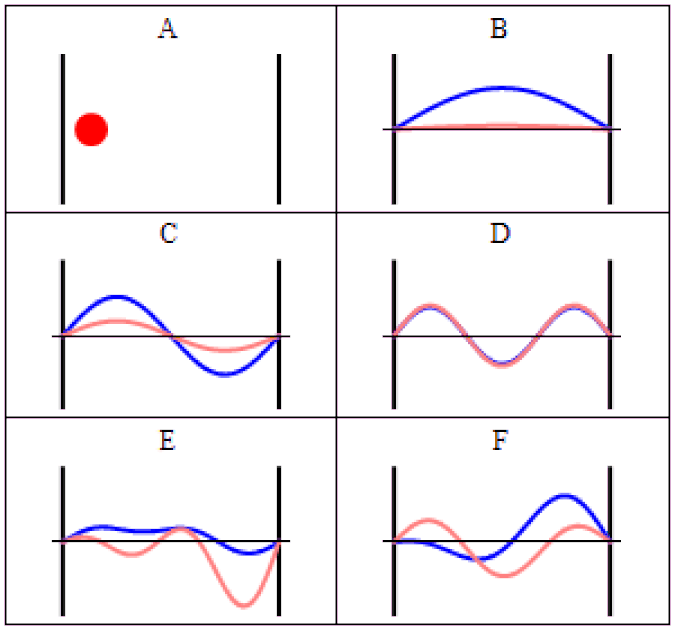
But the way you allowed your system to evolve depended on time, and the notion of time is different for different observers. This was the first existential crisis to face quantum physics.
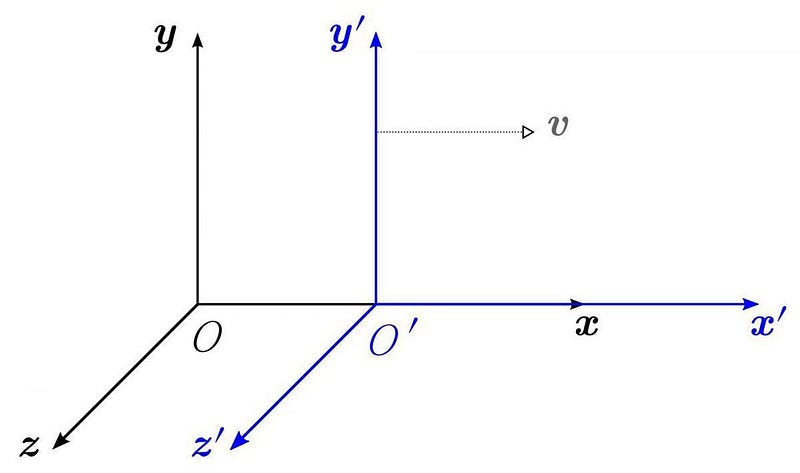
We say that a theory is relativistically invariant if its laws don’t change for different observers: for two people moving at different speeds or in different directions. Formulating a relativistically invariant version of quantum mechanics was a challenge that took the greatest minds in physics many years to overcome, and was finally achieved by Paul Diracin the late 1920s.
The result of his efforts yielded what’s now known as the Dirac equation, which describes realistic particles like the electron, and also accounts for:
- antimatter,
- intrinsic angular momentum (a.k.a., spin),
- magnetic moments,
- the fine structure properties of matter,
- and the behavior of charged particles in the presence of electric and magnetic fields.
This was a great leap forward, and the Dirac equation did an excellent job of describing many of the earliest known fundamental particles, including the electron, positron, muon, and even (to some extent) the proton, neutron, and neutrino.
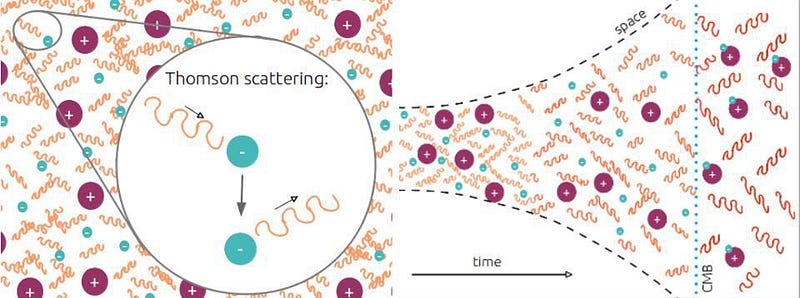
But it couldn’t account for everything. Photons, for instance, couldn’t be fully described by the Dirac equation, as they had the wrong particle properties. Electron-electron interactions were well-described, but photon-photon interactions were not. Explaining phenomena like radioactive decay were entirely impossible within even Dirac’s framework of relativistic quantum mechanics. Even with this enormous advance, a major component of the story was missing.
The big problem was that quantum mechanics, even relativistic quantum mechanics, wasn’t quantum enough to describe everything in our Universe.
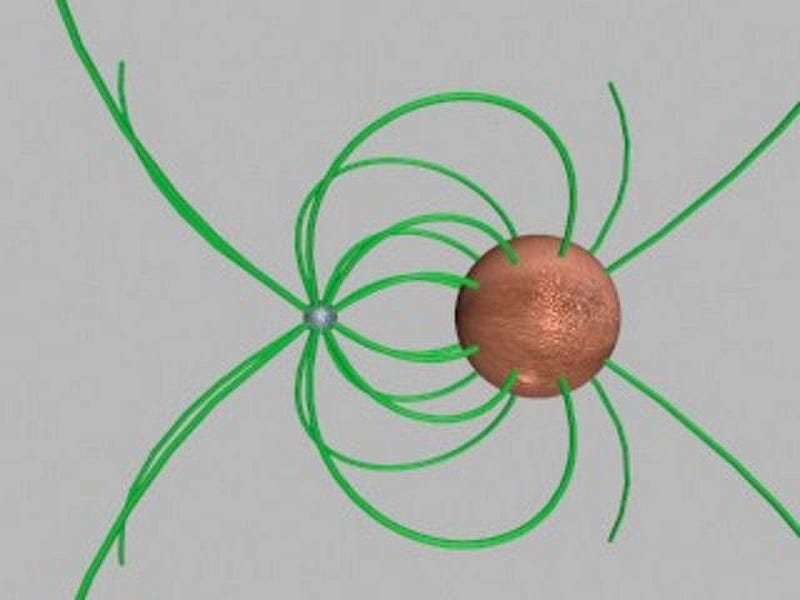
Think about what happens if you put two electrons close to one another. If you’re thinking classically, you’ll think of these electrons as each generating an electric field, and also a magnetic field if they’re in motion. Then the other electron, seeing the field(s) generated by the first one, will experience a force as it interacts with the external field. This works both ways, and in this way, a force is exchanged.
This would work just as well for an electric field as it would for any other type of field: like a gravitational field. Electrons have mass as well as charge, so if you place them in a gravitational field, they’d respond based on their mass the same way their electric charge would compel them to respond to an electric field. Even in General Relativity, where mass and energy curve space, that curved space is continuous, just like any other field.
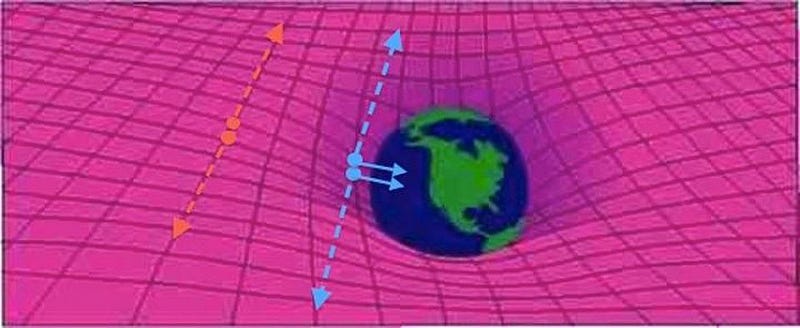
The problem with this type of formulation is that the fields are on the same footing as position and momentum are under a classical treatment. Fields push on particles located at certain positions and change their momenta. But in a Universe where positions and momenta are uncertain, and need to be treated like operators rather than a physical quantity with a value, we’re short-changing ourselves by allowing our treatment of fields to remain classical.

That was the big advance of the idea of quantum field theory, or its related theoretical advance: second quantization. If we treat the field itself as being quantum, it also becomes a quantum mechanical operator. All of a sudden, processes that weren’t predicted (but are observed) in the Universe, like:
- matter creation and annihilation,
- radioactive decays,
- quantum tunneling to create electron-positron pairs,
- and quantum corrections to the electron magnetic moment,
all made sense.
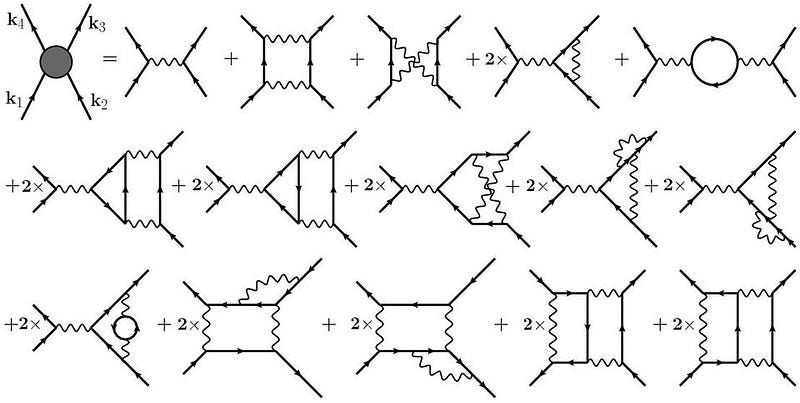
Although physicists typically think about quantum field theory in terms of particle exchange and Feynman diagrams, this is just a calculational and visual tool we use to attempt to add some intuitive sense to this notion. Feynman diagrams are incredibly useful, but they’re a perturbative (i.e., approximate) approach to calculating, and quantum field theory often yields fascinating, unique results when you take a non-perturbative approach.
But the motivation for quantizing the field is more fundamental than that the argument between those favoring perturbative or non-perturbative approaches. You need a quantum field theory to successfully describe the interactions between not merely particles and particle or particles and fields, but between fields and fields as well. With quantum field theory and further advances in their applications, everything from photon-photon scattering to the strong nuclear force was now explicable.
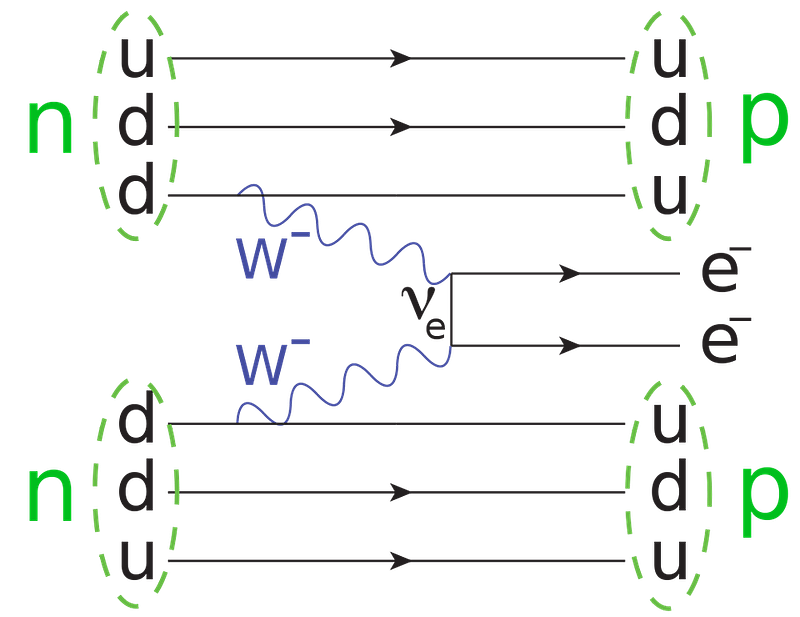
At the same time, it became immediately clear why Einstein’s approach to unification would never work. Motivated by Theodr Kaluza’s work, Einstein became enamored with the idea of unifying General Relativity and electromagnetism into a single framework. But General Relativity has a fundamental limitation: it’s a classical theory at its core, with its notion of continuous, non-quantized space and time.
If you refuse to quantize your fields, you doom yourself to missing out on important, intrinsic properties of the Universe. This was Einstein’s fatal flaw in his unification attempts, and the reason why his approach towards a more fundamental theory has been entirely (and justifiably) abandoned.

The Universe has shown itself time and time again to be quantum in nature. Those quantum properties show up in applications ranging from transistors to LED screens to the Hawking radiation that causes black holes to decay. The reason quantum mechanics is fundamentally flawed on its own isn’t because of the weirdness that the novel rules brought in, but because it didn’t go far enough. Particles do have quantum properties, but they also interact through fields that are quantum themselves, and all of it exists in a relativistically-invariant fashion.
Perhaps we will truly achieve a theory of everything, where every particle and interaction is relativistic and quantized. But this quantum weirdness must be a part of every aspect of it, even the parts we have not yet successfully quantized. In the immortal words of Haldane, “my own suspicion is that the Universe is not only queerer than we suppose, but queerer than we can suppose.”
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.





