Ask Ethan: Why is there no antigravity?

- In Newton’s gravity, all masses attracted one another; there is no “negative mass” to repel. In Einstein’s general relativity, matter and energy curves spacetime, and curved spacetime is experienced as gravity.
- If there were negative mass, or even some sort of negative energy, you might imagine that spacetime could “curve” in the opposite fashion, resulting in antigravity. But this doesn’t describe our Universe.
- This is a profound fact, and makes gravitation very different from other forces, like electromagnetism, that have both attractive and repulsive features. So why can’t there be any “antigravitation” in our Universe?
Although there are four known fundamental forces to the Universe, there’s only one that matters on the largest cosmic scales of all: gravitation. The other three fundamental forces:
- the strong nuclear force, which holds protons and neutrons together,
- the weak nuclear force, responsible for radioactive decays and any “species change” among quarks and leptons,
- and the electromagnetic force, which causes neutral atoms to form,
are all largely irrelevant on cosmic scales. The reason why is simple: the other forces, when you gather large sets of particles together, all balance out at large distances. Matter, under those three forces, appears “neutral” at large scales, and no net force exists.
But not so with gravitation. In fact, gravitation is unique in this sense. With gravitation, there are only “positive” charges: things with positive amounts of mass and/or energy. Between those things, the gravitational force is only attractive, and so cumulatively, it can really add up. But why is it this way, and not any other? That’s what Alex Gebethner wants to know, writing in to ask:
“The common model used to explain spacetime to laymen like me is the bowling ball on a bedsheet. The weight of the ball deforms the flat sheet and draws in smaller objects nearby. But it seems logical that the bedsheet could be deformed in the other direction (upward, to continue with the bedsheet analogy) by a very similar object, pushing objects away from the point of deformation. However, we never observe this occurring. Why? Why does spacetime only bend in one direction (that of gravity)?”
It’s a profound question, and one that deserves a quality answer.

Above is the “classic” illustration of general relativity: the notion that space (and spacetime) is simply a fabric, and that all objects — including both massless and massive objects — exist within this fabric. The more mass (and/or energy) you have in one place, the more space is curved by the presence of that mass/energy, and so the greater the amount that the fabric is deformed. For any object that moves through this region of space, the curvature of that space (i.e., the amount and direction that the fabric is distorted) determines how all entities, both massive and massless, will move through it.
Now, a great many people will object to this picture, because it:
- depicts space as two-dimensional, instead of three-dimensional,
- shows the deformation (or curvature) of space as being in the “down” direction, as though gravitation were causing this deformation (like a bowling ball on a bed), and
- makes it seem like, far away from even a large mass, space is no longer bent at all.
None of these things are true, and so for those of you who have those objections, I’ll encourage you to instead visualize space as a three-dimensional grid. Only, instead of a “Cartesian” grid, where all the lines are mutually perpendicular in all three dimensions, think of it as a grid where lines get “sucked” inward by the presence of masses, as though someone grabbed a bunch of strings from a Cartesian grid and pulled them all in toward a single point.

The big question that we need to consider is why gravity can’t work in a repulsive fashion as well: things only gravitate; they don’t seem to anti-gravitate. It’s as though space can only “curve” in one direction: the direction that makes things attractive, not repulsive. In the “2D bedsheet” analogy, matter and energy only ever cause space to curve “down,” never “up,” and so there’s only attraction, not repulsion. In the “3D grid” analogy, matter and energy only ever cause those lines to be drawn “inward,” never “outward,” and again, there’s only attraction, not repulsion.
There’s a profound and important reason for this that gets straight to the heart of what makes gravitation not only remarkable, but unique, among the four fundamental forces: there’s only one “sign” for the type of gravitational “charge” in the Universe: a positive one.
Think about that for a minute, because it’s not typically the way we conceive of gravitation. We don’t talk about gravitational charges; we talk about things like “mass” and “energy” when it comes to gravity. But of all the physical entities, both macroscopic and down on a quantum level, that have been demonstrated to exist, there’s no such thing as “negative mass” or “negative energy” that’s ever been discovered. Mass and energy, overall, must always be positive.
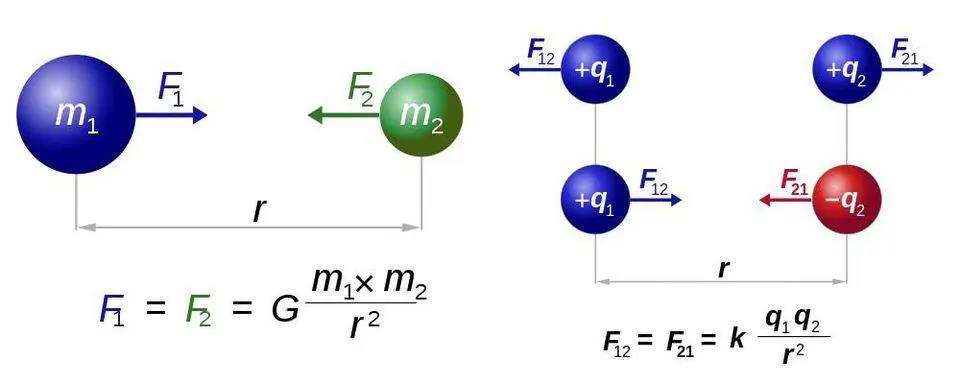
Compare this up against a force like electromagnetism, and you’ll immediately see the difference. When it comes to a phenomenon like electric charge, you don’t just have “one type” of charge; you have two: positive (+) and negative (-). Under the rules of electromagnetism:
- positive and positive charges repel,
- positive and negative charges attract,
- negative and negative charges repel, and
- negative and positive charges attract.
In other words, the sign of the electromagnetic force — which direction the net force on each particle points — is dependent on whether the charges are alike (in which case they repel) or opposite (in which case they attract).
The electromagnetic force, as it turns out, is much stronger than the gravitational force: if you put two (positively charged) protons close together and measured the (repulsive) electric force and compared it to the (attractive) gravitational force, you’d find that repulsion wins… by a factor of about ~1036, or, written out, 1,000,000,000,000,000,000,000,000,000,000,000,000.
So why doesn’t the electric force dominate the Universe, instead of the gravitational force?
The answer is that the Universe is electrically neutral, where the amount of positive charge and the amount of negative charge balance out. Atoms are electrically neutral, with the positive electric charge of the nucleus exactly balanced by the negative electric charge of the electrons that orbit it. Planets, stars, and galaxies are predominantly made of atoms as well, and are electrically neutral overall. The reason the gravitational force is so important — arguably, the only important force on extremely large cosmic scales — is because even though it’s so tiny, it’s cumulative. There’s only one type of gravitational charge, and it adds up over time.
The other two (nuclear) forces are also prohibited from affecting large scales. For the weak nuclear force, it’s the fact that the force is mediated by extremely massive particles: the W-and-Z bosons. Because these particles are so much more massive than the particles that experience the weak interaction, these interactions are suppressed very strongly. It’s only through the process of quantum tunneling, from an (unstable) initial state to a (more stable) final state, that the weak interactions can typically proceed. At greater distances, the suppression is greater, and so on scales greater than a subatomic particle, the weak interaction plays no role at all.
For the strong nuclear force, the situation is a little more complicated. The strong force is mediated by gluons, and gluons are massless, like photons (which mediate the electromagnetic force). Unlike the gravitational force (which has one type of charge) or the electromagnetic force (which has two types of charge), the strong nuclear force actually has three types of charges that are all interrelated. We typically use a color analogy when it comes to the strong force, where:
- red, green, and blue are the three colors,
- cyan, magenta, and yellow are the three anti-colors,
- that a color plus its anticolor (red and cyan, green and magenta, blue and yellow) is colorless,
- and where three colors combined (red+green+blue) or three anticolors combined (cyan+magenta+yellow) also makes a colorless combination.
Only quarks and gluons have color among the fundamental particles, and the only states that quarks and antiquarks can exist in are colorless states: baryons (three quarks), anti-baryons (three antiquarks), mesons (quark-antiquark combinations), and more complex, shorter-lived states such as tetraquarks (two quarks and two antiquarks) and pentaquarks (four quarks and one antiquark or four antiquarks and one quark).
Because only bound, colorless states of quarks exist in nature, the force between any of these bound states must also occur through a colorless combination that conserves baryon number: therefore, the mesons. Because all mesons are massive, this “residual strong force,” as it’s known, is also short-range, just like the weak nuclear force.

On cosmic scales, that just leaves us with gravity. All masses are positive, all energies are positive, and since it’s the mass/energy in space, at all locations, that determines spatial curvature, and spatial curvature determines gravity, the gravitational force must always be attractive.
Now, that’s with the Universe that we (apparently) have: the Universe as we know it. But we could have imagined a very different Universe: one where either negative mass or negative energy states could exist. Unlike the electromagnetic force, where like charges repel and opposite charges attract, gravitation would be flipped:
- positive mass/energy states would attract positive mass/energy states,
- positive mass/energy states would repel negative mass/energy states,
- negative mass/energy states would attract negative mass/energy states, and
- negative mass/energy states would attract positive mass/energy states.
Were negative mass/energy states a part of our reality, we’d be able to manipulate them in some very clever, important ways. We could move negative states around in such a way that they could “shield” us from the gravitational force, allowing us to experience weightlessness without needing to be in free-fall.

We could create spacecrafts where the floors were made of positive energy states, in space, and atop them, the ceilings could be made of negative energy states, enabling us to create a uniform “artificial gravity” field in the same way that an electromagnetic capacitor creates a uniform electric field inside of it.
And, perhaps most remarkably, with large enough amounts of positive and negative energy states at our disposal, we could use these dual negative energy and positive energy states to create a warp field: where
- the space in front of a spacecraft is positively curved, and contracted,
- the space behind the spacecraft is negatively curved, and expanded/rarified,
- and the space where the spacecraft is located is flat, preventing it from being destroyed/damaged by gravitational tidal forces.
This is the big idea behind the Alcubierre drive: the solution within general relativity that allows for a realistic warp drive, contingent on the existence of negative mass/energy states. One great hope for a realistic warp drive was the possibility that antimatter, even though it has positive mass from Einstein’s E = mc², would behave as though it had a negative gravitational mass. When put to the test in a gravitational field, however, it was shown that was not the case, crushing our greatest hope for a realistic warp drive without needing to invoke new physics.
Is there any circumstance that doesn’t require “new physics” where we could actually observe or test the effects of gravitational repulsion? Are there any configurations we can imagine or create, under which the gravitational force can be effectively negative, instead of positive?
Yes, you can design one. Instead of starting with empty space, imagine that space is uniformly filled with matter: like a massive, perfect fluid. Now, imagine that within this fluid, you have two types of “particle” to put down:
- a positive mass particle, whose density is greater than the density of the fluid (e.g., a lead particle in a fluid like water),
- and (effectively) a negative mass particle, whose density is lower than the density of the fluid (e.g., a solid-walled balloon, or an impermeable aerogel, in a fluid like water).
Under these circumstances, we can actually observe what’s gravitationally attractive and what’s repulsive. As you might expect:
- two positive mass particles attract one another,
- two negative mass particles attract one another,
- but one positive mass and one negative mass particle repel one another.
There isn’t a “fundamental” repulsion, but if you fill your Universe with mass/energy and have a stable region that has less of it, that region behaves as though it possesses negative mass/energy, with the precise consequences described above.

However, on a fundamental level, there are no negative mass/energy states to speak of. As determined by measuring the cosmological constant (i.e., the effects of dark energy), the total amount of energy inherent to empty space is positive — small, but greater than zero — and that there’s nothing you can remove or take away from space to drive that energy to a less-than-zero (i.e., negative) value. Sure, you can manipulate space to create lower energy states in one region than another, and you can leverage that phenomenon to create an effectively negative (relative to the average mass/energy state) energy region, but it’s still a region where the gravitational force is attractive. It’s just “less attractive” than the surrounding regions.
If you have a helium balloon floating in your car and slam on the brakes, all the passengers will jerk forward, but the balloon will float to the back. It isn’t because the balloon violates Newton’s law of “an object in motion remaining in motion,” but because the (denser, heavier) air in the car “remains in motion” more strongly than the (less dense, lighter) helium balloon. That is the only sense in which we have antigravity, where something with less mass/energy than average can behave like a negative source of gravity: negative compared to something that’s “more positive.” Unless, or until, some sort of new physics is discovered that shows that negative mass or negative energy states can exist, antigravity, at least at a fundamental level, will remain a mere mathematical curiosity.
Send in your Ask Ethan questions to startswithabang at gmail dot com!