Why Supersymmetry May Be The Greatest Failed Prediction In Particle Physics History

It was so well-motivated and compelling. But the particles never appeared.
Every so often, an idea comes along in theoretical physics that’s undeniably profound. When a single idea can solve a slew of existing puzzles in one fell swoop while simultaneously making new, testable predictions, it’s bound to generate a tremendous amount of interest. It can do more than provide a potential way forward; it can capture the imagination as well. If its predictions are borne out, it could kick off an entirely new understanding of the Universe.
This was exactly the situation when physicists hit upon the idea of supersymmetry, or SUSY for short. No one knows why the fundamental particles of the Standard Model have masses that are so small compared to the Planck scale, or why the fundamental constants don’t unify, or what dark matter might be. But SUSY promised a solution to each of these, while predicting a spectrum of new particles. With the LHC’s Run II complete, we know those particles aren’t where they need to be. The dream of solving all of these problems with SUSY has vanished, and a generation of physicists must now confront that reality.
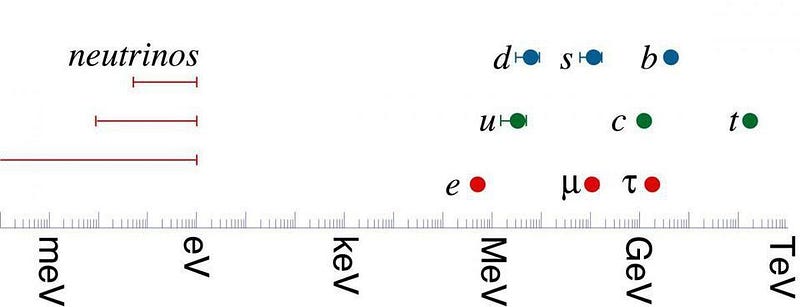
The motivation for SUSY has its origins dating back to the early days of quantum mechanics, and the problem of the electron. The electron, you see, is a problem because we know that it has no physical size — it is a point particle — but it does have an electric charge. Whenever you have a charge, it produces both an electric field and a voltage (electric potential) around it. Since it has a charge itself, it’s capable of feeling the potential that it generates on its own: it has an energy inherent to its own existence. The smaller the size of an electron, the larger its own internal energy would be, which means that if the electron is truly point-like, it has to have an infinite amount of energy inherent to it.
Of course, this isn’t the case. The electron has a finite amount of energy inherent to it, defined by its rest mass and Einstein’s famous equation: E = mc².

If you ask, based on the laws of electromagnetism, what the size of the electron should be so that its own electric energy accounts for its mass, you get a diameter of about 5 × 10^-15 m, or a size that’s even larger than the proton. Clearly, that isn’t right!
The way out was the quantum mechanical existence of antimatter, and of the positron (or the anti-electron) in particular. In quantum physics, remember, the vacuum isn’t just empty, unoccupied space, but rather consists of a slew of virtual particles that pop in and out of existence, and that includes electron-positron pairs.
Not only can the electron produce a photon to cause it to interact with itself, but it can also annihilate with the positron in an electron-positron pair fluctuation, leaving only the “fluctuation” electron behind. When you do the calculation, you find that these two contributions nearly cancel, leading to the electron’s tiny size despite its (relatively) enormous charge.
“Okay, fine,” you acquiesce, “that’s a nice victory for the quantum Universe. But what does that have to do with SUSY?”
The big idea is that this quantum cancellation only occurs because there’s a symmetry in the theory — between matter and antimatter — that protects the properties of the electron, enabling it to have the combined mass, size, and charge properties that it has.
The big idea of SUSY is that there could be an additional symmetry present — between fermions and bosons — that similarly protects the properties of matter and enables the particle masses to be so small compared to the Planck scale. Instead of particle masses of around 10¹⁹ GeV/c², we’d have particle masses some 17 orders of magnitude smaller than that. All you’d need is a superpartner particle for every one of the Standard Model particles that exists.
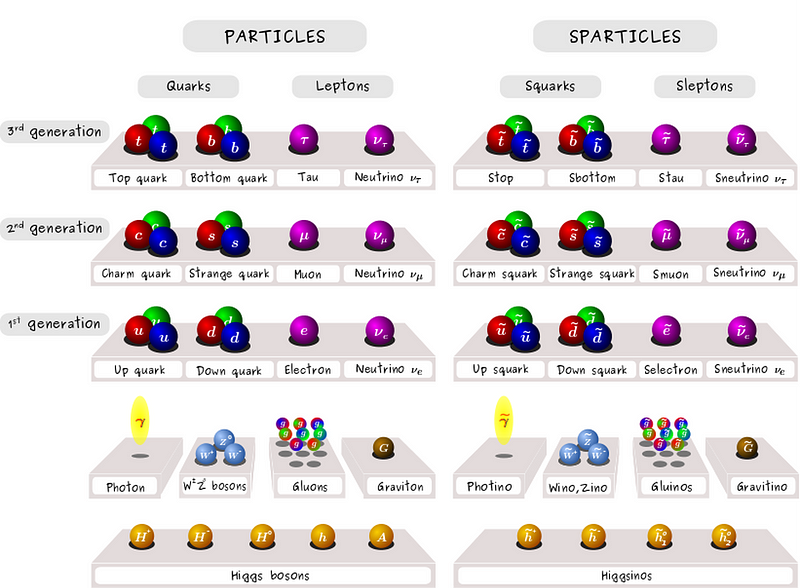
Sure, you have to double the number of known fundamental particles, creating a superpartner particle counterpart (a super-fermion for each Standard Model boson; a super-boson for each Standard Model fermion) for every one that’s known. But this symmetry between fermions and bosons can, in theory, reduce those particle masses all the way down to the values we observe.
If these new supersymmetric particles come in at approximately the electroweak scale, or between about 100 GeV and a few TeV, they can also:
- be created and measured at LHC energies,
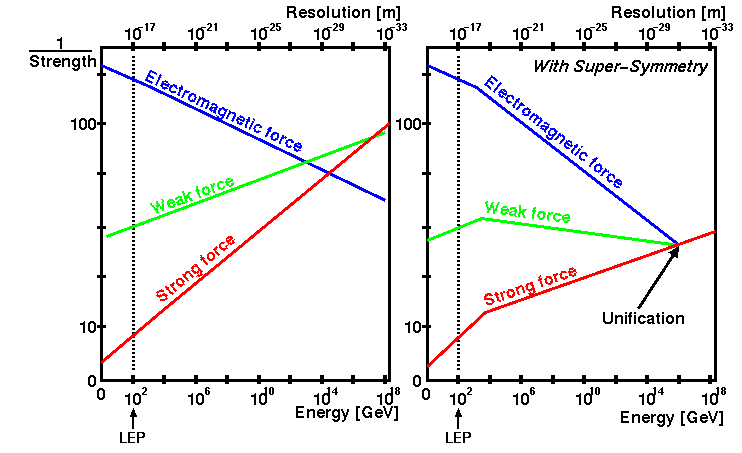
- cause the coupling constants of the three quantum forces (electromagnetic, weak, and strong nuclear forces) to unify at approximately the theoretical grand unification (GUT) scale,
- and can create a neutral, stable supersymmetric particle that’s an excellent candidate for the Universe’s dark matter.
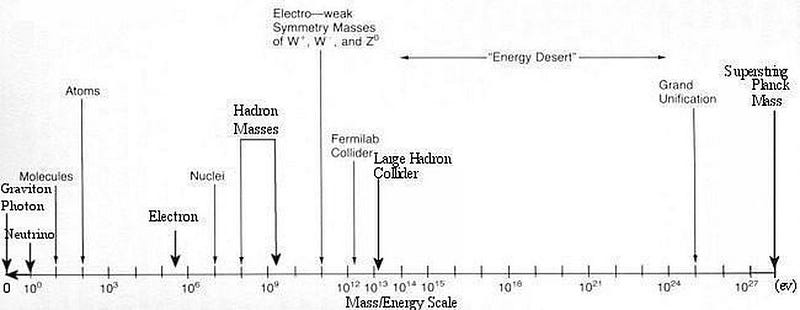
There are a few fundamental constants in nature: the gravitational constant (G), Planck’s constant (h or ħ, which is h/2π), and the speed of light ©. There are different combinations of these constants we can create to get values for time, length, and mass; these are known as Planck units. If you were to predict the mass of the particles in the Standard Model from first principles, they ought to be on the order of the Planck mass, which has an energy of around 10²⁸ eV/c². The major problem is that this mass is 17 orders of magnitude, or a factor of 100,000,000,000,000,000 larger than the heaviest observed particle in the Universe.
The Higgs boson, in particular, should have the Planck mass, and — since the Higgs field couples to the other particles, giving them mass — so should all the others. That we observe it to have a mass of merely 1.25 × 10¹¹ eV/c² tells us there ought to be something extra at play.
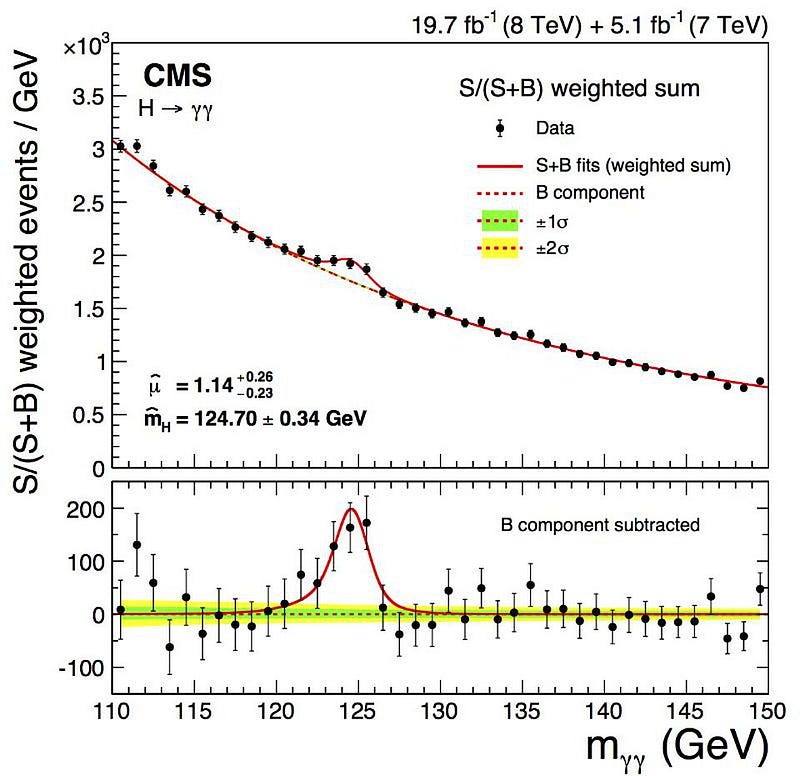
In theory, SUSY is a possible solution to this puzzle, where practically no other known solutions remain viable. However, just because it offers a possible solution doesn’t mean it’s correct. In fact, each of the predictions of SUSY are extremely problematic for physics.
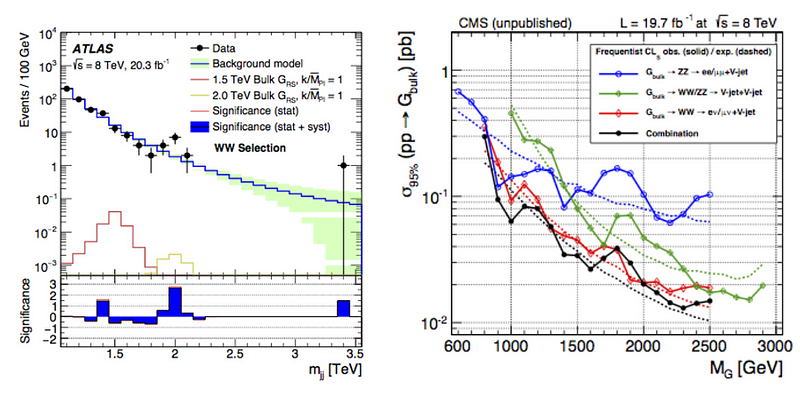
- If SUSY is the solution to the hierarchy problem, then the lightest superpartners should definitely be accessible by the LHC. The fact that it hasn’t found any, thus far, is enough to eliminate virtually all models of SUSY that solve the very problem it was designed to solve.
- The strong force may not unify with the other forces. There’s no evidence for unification in our Universe so far, as proton decay experiments have come up empty. The initial motivation is flimsy here as well: If you put any three curves on a log-log scale and zoom out far enough, they will always look like a triangle where the three lines just barely miss coming together at a single point.
- If dark matter is truly made of the lightest SUSY particle, then experiments designed to see it such as CDMS, XENON, Edelweiss and more should have detected it. Furthermore, SUSY dark matter should annihilate in a very particular way which hasn’t been seen.
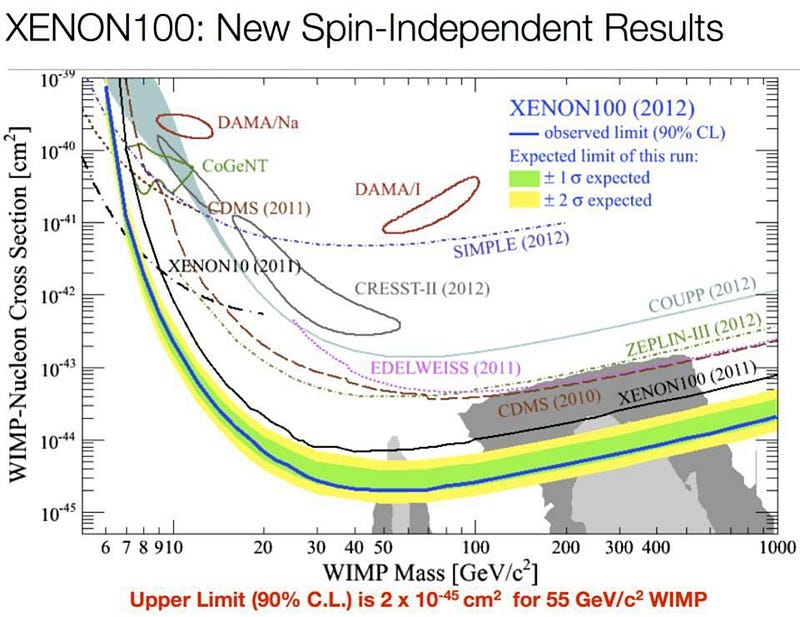
The collider limits themselves are particularly damning for this idea. If you want SUSY to solve the problem of why the masses are as small as they are, you need at least one of the superparticles you can create to be of the same order of magnitude as the heaviest Standard Model particles.
This was one of the major signatures that the LHC was designed and built to see. Those particles simply aren’t there, and at this point, the mass limits on them have risen to such enormous magnitudes that theorists can no longer solve the hierarchy problem with SUSY alone. Instead, some additional mechanism must exist — such as the split SUSY scenario — to explain why the particle masses are so small and the superpartner masses are so large. In other words, the original motivation for this beautiful, elegant, and compelling theory is no longer the current primary motivator for SUSY at all. It wasn’t successful at the very thing it was designed to do.
It’s important to know what SUSY is, because of the fact that it is such a theoretically compelling idea. It solves problems that no other competitor does in an elegant and powerful way. It makes new predictions that can be tested, and those tests have largely now been performed. Unfortunately, the answer thus far is that SUSY, as interesting as it may be, does not appear to describe our Universe.
As always, continued experimentation will be the ultimate arbiter of nature, but no reasonable person can justifiably conclude that SUSY is supported by the evidence. If SUSY is wrong, a lot of people will have invested their entire careers in one of the most interesting blind alleys we’ve ever gone down. If there is no SUSY in nature at any energy scale (including the Planck Scale, although this will be a challenge to test), then string theory, which leads to SUSY, cannot describe our Universe.

There are two very different camps of scientists when it comes to the issue of SUSY. On the one hand, we have a large group of people, both theorists and experimentalists, who are following the evidence closely, seeking alternative explanations for these various puzzles, and responsibly constraining the viable scenarios to progressively tighter bounds. To rule out a theory that has dominated a sub-field of physics for nearly two generations would be a tremendous advancement for science.
But on the other hand, there’s a large and powerful group of (mostly) theorists who will go to their graves as true believers in not only SUSY, but electroweak-scale SUSY, regardless of what the evidence says. Yet with every new proton the LHC collides, we see the same answer again and again: no SUSY. No matter how often we fool ourselves, nor how many scientists get fooled, nature is the ultimate arbiter of reality. The experiments do not lie. As of today, there is no experimental evidence in favor of SUSY.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.





