Yes, Virginia, Black Holes Exist!
Do black holes exist? The world’s most famous scientist vs. the actual science.
“My goal is simple. It is a complete understanding of the Universe, why it is as it is and why it exists at all.” -Stephen Hawking
Here in our little corner of the Universe, the Earth is a pretty intense source of gravity for us. If we want to escape its gravitational pull, we’d need to accelerate ourselves up past the escape velocity, or the speed necessary to climb out of the gravitational potential well that Earth’s mass creates. We can (and have) accomplished this, in fact, but it would take a speed of around 11.2 km/s (or 0.004% the speed of light) to make it so.

But that’s not so fast, after all, not compared to a great many things in this Universe. The reason that we don’t need higher speeds to escape from our planet is that despite having a decent amount of mass — some 6 × 10^24 kg, or some 10^49 heavy atoms — our Earth is spread out over a relatively large volume of space.
But if the laws of physics were somewhat different, we might be able to compress the mass of our Earth down into a much smaller region of space. And if we could, it would take greater and greater speeds to escape from it. At some point, when all the mass of the Earth was compressed into a sphere a little smaller than a centimeter in radius, you’d suddenly discover that nothing in this Universe — not even light — could escape from it.
You’d have turned the Earth into a black hole.
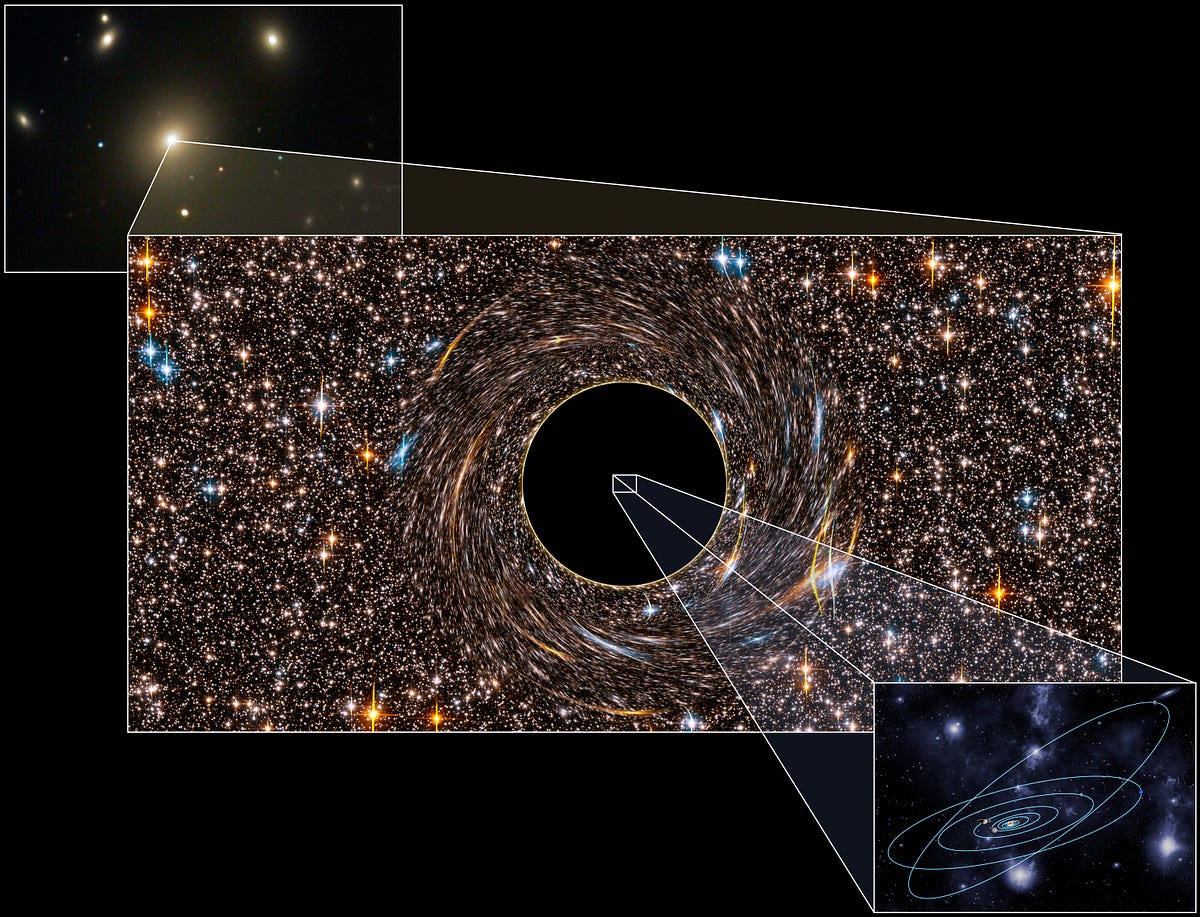
Because the speed of light in a vacuum is a universal speed limit, some regions of space can achieve enough mass compressed into a small enough volume that nothing can escape from it. For a long time, these were purely theoretical objects, as it was assumed that getting such huge amounts of mass into such a tiny volume would be impossible. But then we started discovering things that were… interesting.
Regions of space with incredible radio and X-ray emissions, but no visible light. Regions where stars were being ripped apart and their matter accelerated, but no signs of ultramassive stars. And finally, a place near the very center of our galaxy where stars were orbiting a single point that must have a mass of around 4 million Suns, but from which no light of any type was being emitted.
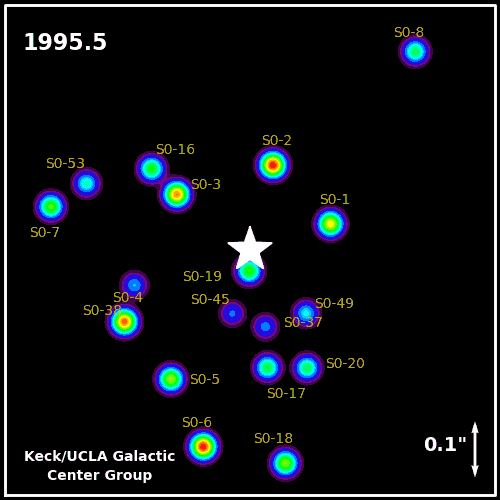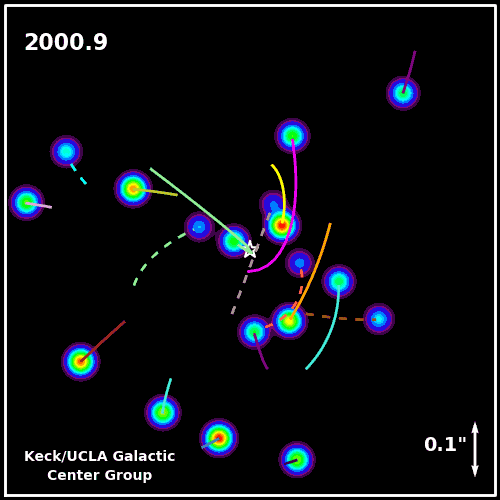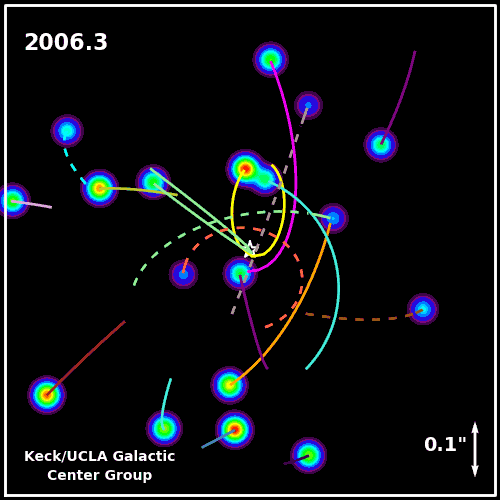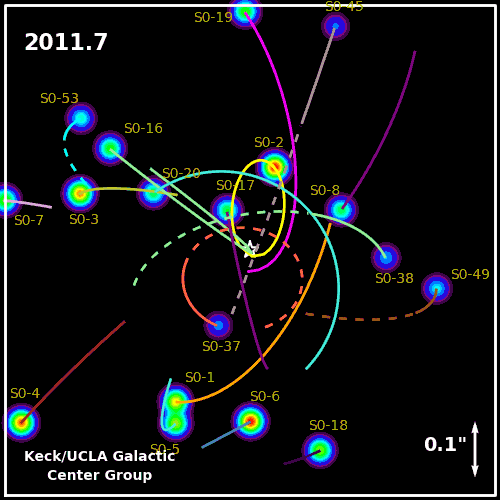
This must be a black hole! Gravitationally, Einstein’s theory of General Relativity tells us that black holes must distort space, with interesting optical effects that can will show up by looking at the background matter.

But you might wonder, thinking about objects like this, whether they’re really, truly, completely black, in the sense that nothing can ever escape from them. It’s a legitimate question, and one that didn’t really go answered for a very long time. You see, black holes — as described by Einstein’s theory of gravity — were classical objects, or objects described by a continuous spacetime with mass, charge, and angular momentum in it. But we know that the matter and energy in our reality is not necessarily continuous in nature, but rather quantum. And there was no good way to reconcile the fundamentally quantum nature of things with a classical theory like General Relativity.

Instead, the Universe itself must be inherently quantum in nature, and yet we do not have a quantum theory of spacetime. In the absence of a quantum theory of gravity, there was only one option if you wanted to know what was happening around a black hole: you’d have to compute the predictions of our quantum Universe — and that’s the full-on quantum field theory — in the curved spacetime as predicted by General Relativity.
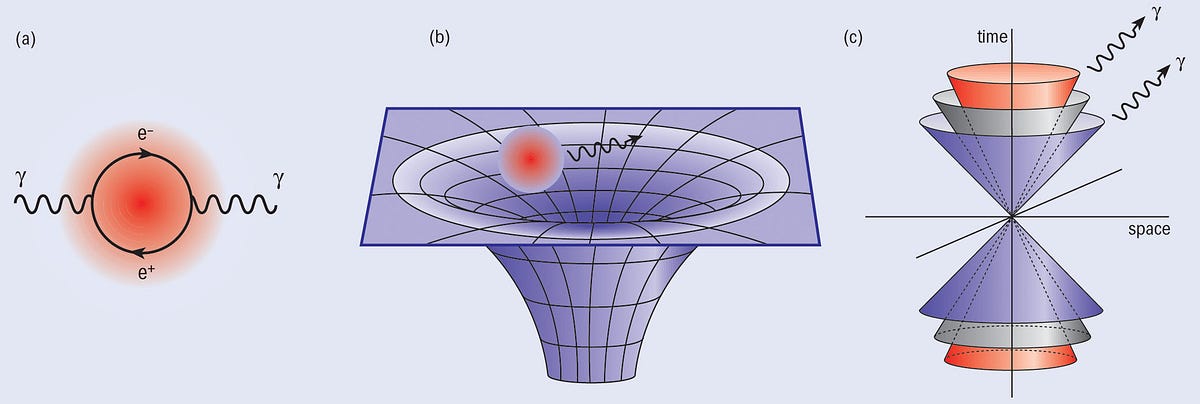
It wasn’t going to be easy. And I know, because I’ve done the calculation myself, but I wasn’t the first to do so. That honor goes to Stephen Hawking, who — in the mid-1970s — calculated what would happen when you had a fundamentally quantum Universe existing in curved spacetime, and that the curvature of space was due to the presence of a black hole.
You’d have quantum fluctuations, or pairs of particles-and-antiparticles popping in-and-out of existence, while simultaneously having this event horizon nearby, where things could fall in, but nothing could ever get out.
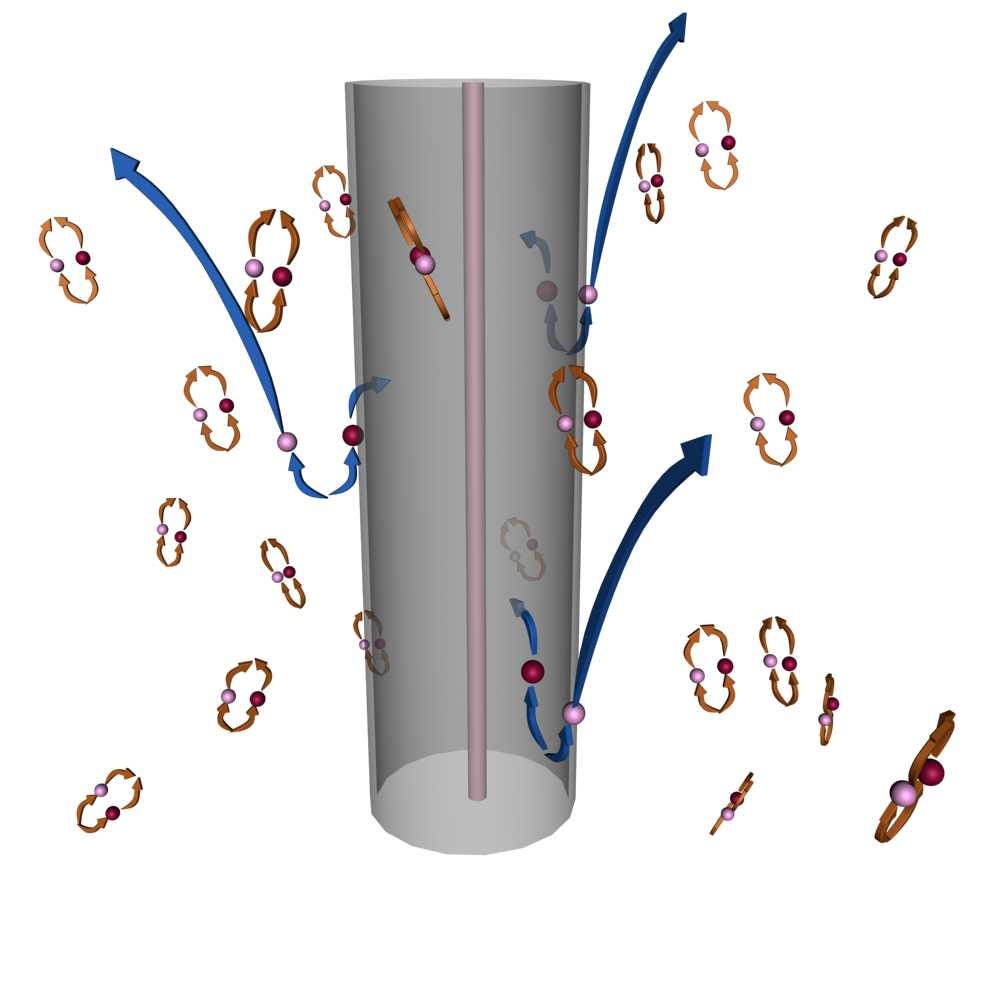
What would sometimes happen, however, is that if you had a fluctuation just outside the event horizon, one of the particles (or antiparticles) would sometimes escape from the black hole, while the other one fell in! Because of the conservation of energy, the black hole had to lose mass, while the escaping radiation’s spectrum (and you need quantum field theory to get the spectrum correct) would be a blackbody, and determined by the mass of (and hence curvature near) the black hole! All the other properties — how long the black hole would exist for, the timescales on which it would evaporate, the rate of energy loss — were determined by this phenomenon, which is justly known as Hawking radiation.
In other words, black holes aren’t completely black!

Because we don’t yet have a complete, comprehensive theory of quantum gravity, we have to do the best we can with the tools we have: General Relativity as the descriptor of space and time, Quantum Field Theory as the laws governing matter and energy. As you (theoretically) move in towards a black hole, you’ll typically pass an accretion disk, you’ll find that there’s an Innermost Stable Circular Orbit, and then interior to that, there shouldn’t be anything, as the black hole gobbles that up and takes in inside its event horizon in short order. And once you go inside — with the exception of Hawking radiation — nothing can ever leave.
Unless, of course, as a now-famous paper from two years ago contended, you get incinerated by a firewall of radiation as you cross the event horizon.

What that paper showed is that all three of the following cannot be simultaneously true:
- Hawking radiation is in a pure state.
- The information carried by the radiation is emitted from the region near the horizon, with low energy effective field theory valid beyond some microscopic distance from the horizon.
- The infalling observer encounters nothing unusual at the horizon.
This is an interesting paradox, because we had previously thought that Hawking radiation avoids information loss, the black hole’s event horizon is a real entity from which nothing can escape, and there would be no firewall (i.e., “nothing unusual”) when you cross the event horizon. Yet, could one of these three things be wrong? And if so, which one?
It’s often true that noticing things like this is how physics moves forwards. But it’s also true that the resolution to this paradox — or any paradox in science — isn’t dependent on what a titanic, famous, authoritative figure in the field says it is. It’s dependent on the scientific merits themselves.

But three physicists that you’ve probably never heard of — Samuel L. Braunstein, Stefano Pirandola, and Karol Życzkowski — came up with an interesting find last year! You see, Hawking radiation comes from pairs of entangled quantum particles, one of which “escapes” out into the Universe and the other one of which falls into the black hole. If you break the entanglement, by say, measuring the properties of the one that didn’t fall in, a barrier of energetic particles would descend around the event horizon of the black hole; that’s where the alleged firewall comes from. You have a particle that went “in” and one that went “out,” and they’re entangled with one another: hence the paradox.
The fun thing that they found, here, is that the greater the entanglement across the event horizon of the black hole, the later the firewall curtain falls. More entanglement = more time. And in our Universe — as their paper shows — entanglement across all black hole event horizons is maximized, which means that the time it takes the firewall curtain-to-fall is… infinite. So that was a clue; it didn’t answer everything, but it told us that the problem with the paradox probably isn’t that item #3 is wrong.
But then this happened.
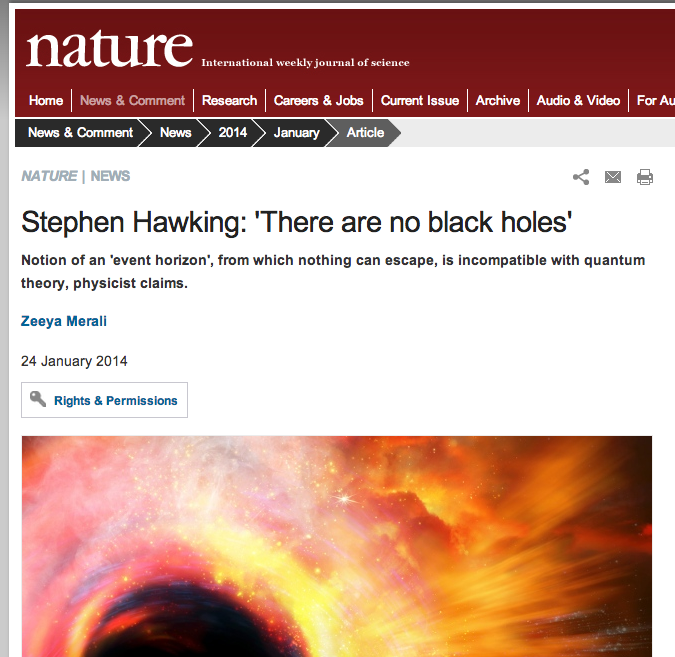
In short, this proposal suggests throwing out #2, or the notion of a classical event horizon. Well, maybe that’s the case, but it’s far from clear that this is even a self-consistent resolution, much less the correct one. I do have to give credit for the astonishingly successful PR move to claim, “There are no black holes,” but the quantum nature of our Universe in no way invalidates our notion of a classical event horizon in any way other than the existence of Hawking radiation invalidates it.
On the other hand, if it has been successfully shown that #3 isn’t the solution, maybe it’s worth looking into #1? That is, we normally think of avoiding information loss (another way of saying that Unitarity is maintained) as being synonymous with giving rise to a pure state of radiation. But what if we could avoid that information loss without the Hawking radiation being in a so-called pure state?
There have been two very interesting papers on that front that — along with the Braunstein, Pirandola and Zyczkowski paper I linked to above — represent (to me) the three biggest developments that have come about since the statement of this paradox. And none of them have names like Hawking or Susskind attached to them.
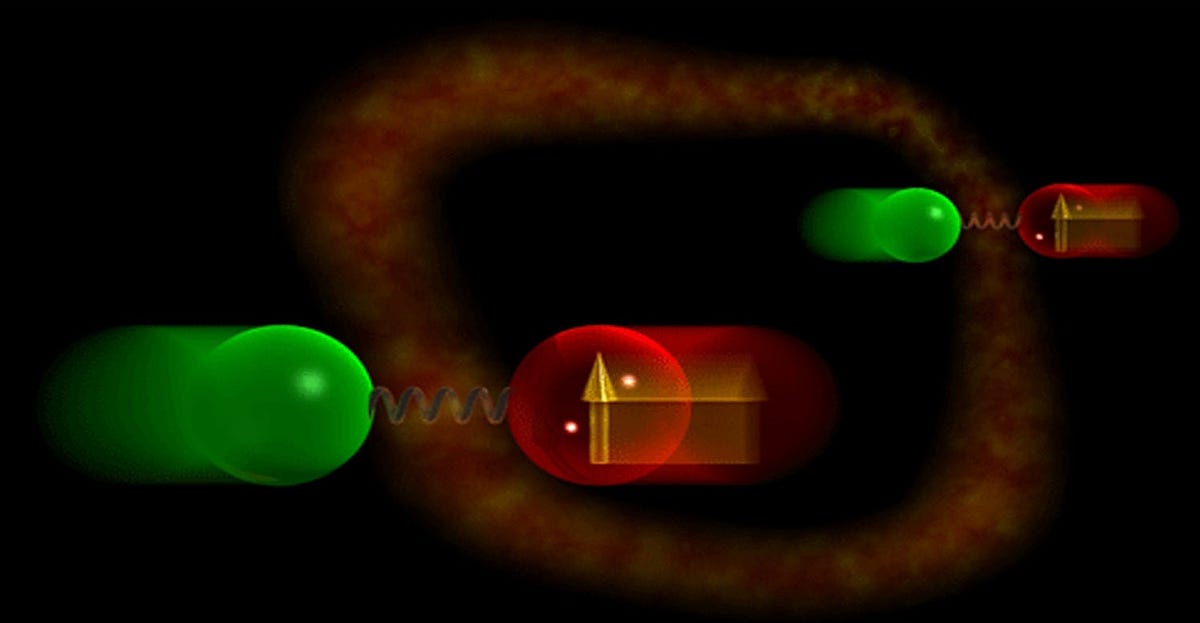
Imagine you have two pairs of particles with the same momenta, and for both pairs, one particle falls in through the event horizon while the other escapes out. If the two that fall in (and, because they do, you never get to see their information) are each entangled with the ones that escape out, you lose information, as you no longer have that Unitarity property.
But Verlinde and Verlinde showed that you can do a mathematical (and also Unitary) swap so long as the two pairs have the same momenta as one another. Instead of having an in-out pair and another in-out pair, you can treat them as though they were an in-in pair and an out-out pair, effectively disentangling* them, meaning that there’s no longer any entanglement across the horizon, and hence no possibility of a firewall. That was progress, but it didn’t demonstrate exactly where the firewall paradox broke down.

Until, quite recently, Sabine Hossenfelder found quite generally that the information preserving transformations you can do also have some generic and incredibly interesting properties:
- The swap to disentangle the particles — so that there’s no information crossing the event horizon — can be local, meaning it can happen between two points that are causally connected at all times.
- This local interaction is restricted to occurring in a certain location right outside the event horizon; you do not get a choice!
- And finally (and most importantly), she finds that there are no entanglements between radiation states emitted at significantly different times, something that you need if you’re going to be a “pure state.”
And so what these three papers, in tandem, have done, is demonstrate that there is no firewall and that the resolution to the firewall paradox is that the first assumption, that Hawking radiation is in a pure state, is the one that’s flawed.

You won’t read about this in the popular write-ups because it doesn’t have a catchy headline, it’s complex, and it’s not work by someone that’s already very famous for other work. But it’s right. Hawking radiation is not in a pure state, and without that pure state, there’s no firewall, and no paradox.
There is still an incredible amount to learn and understand about black holes, event horizons, and the behavior of quantum systems in strongly curved spacetime, to be sure, and there’s lots of very interesting research ahead. These findings arguably raise more questions than they answer, although at least we know that black holes won’t fry you when you fall in; it will still be death by spaghettification, not by incineration!

And that’s the actual end of the Black Hole Firewall Paradox!
* – A tremendous thanks to Sabine Hossenfelder, author of this paper, for explaining many of her thoughts and many of the nuances of this topic to me. You can read her admonition of the outrageous Hawking claims here.




