Ask Ethan: Is alien space travel limited by the speed of light?

- For all types of matter and energy that exist in the Universe, there’s a limit to how quickly each and every quantum can move through the fabric of space: the limiting speed of light.
- While that might seem like the incontrovertible speed limit for any spacefaring civilization, no matter how advanced, there are a few clever tricks, mostly involving general relativity, that might circumvent it.
- Is it possible to leave point “A” and arrive at point “B” in less time than it would take to travel from “A” to “B” at the speed of light? If so, alien civilizations may have already gotten there. Here’s how.
When we speak about the distance to cosmic objects — distant stars, galaxies, quasars, and more — we usually measure them in light-years. This is because of the understanding that any form of matter, regardless of what you do to it or how much kinetic energy you add to it, can only approach, but never reach, a maximum speed limit set by the laws of physics themselves: the speed of light. Only massless entities, things like photons, gluons, and gravitational waves, can actually achieve that maximum speed of 299,792,458 m/s through the fabric of space, while everything else is doomed to travel more slowly, never being able to attain that speed while still obeying the laws of physics.
Does that necessarily mean that even the most advanced alien species imaginable, including us arbitrarily far into the future, will forever be unable to travel through space in any swifter, more rapid fashion? That’s the question sent in by Stephen Johnson, who asks:
“Can we safely assume that alien space travel is limited by the speed of light? This is baked into assumptions about how aliens might travel. (Obviously, there are highly speculative, sci-fi alternatives: wormholes, etc.) But is it arrogant to confidently declare that aliens are limited by a “cosmic speed limit,” given the long history of discoveries upending scientific thought?”
Although the conservative expectation is that yes, the speed of light is an insurmountable limit, there are a couple of very good reasons to believe that perhaps there may be a way around it. Perhaps, even without invoking a new law of physics, the speed of light may not set the ultimate limit after all. Here’s how.

Conventional motion
When most of us think about traveling from one point to another, we think about traveling there along the shortest distance possible: in a straight line. If you want to minimize your travel time, you’ll take the shortest path and move as fast as possible, which makes sense not only in conventionally non-relativistic (i.e., Newtonian or Galilean) motion scenarios, but also if we include Einstein’s special relativity.
The rules of special relativity are a little bit counterintuitive, as they state that motion, times, and distances are all relative between each and every observer, and there’s no such thing as an “absolute” motion, time, or distance that can be measured that all observers will agree upon. The one thing that is absolute, perhaps bizarrely, is the speed of light, which all observers will always measure to have the same value: 299,792,458 m/s.
You can imagine accelerating yourself in a spaceship at a constant rate, faster and faster as you like, without any end, as you move from your starting point to your destination. But if you accelerated at the same acceleration we experience here on Earth, 9.8 m/s², for 12 full lunar months (354 days), you wouldn’t reach the speed of light, despite accelerating for a full 30,591,070 seconds, even though, mathematically, 30,591,070 s × 9.8 m/s² = 299,792,458 m/s.
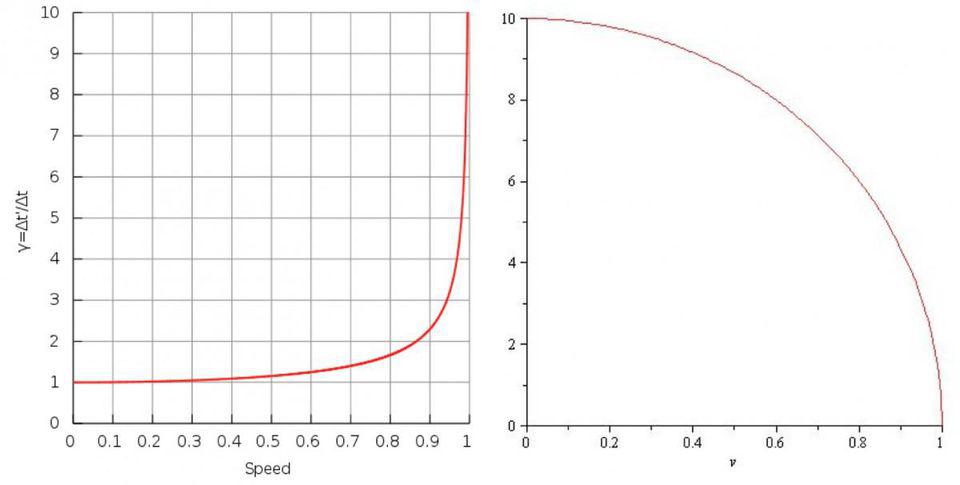
This is because you can’t simply add velocities the way you’re used to. If you’re traveling at +15 m/s and you throw a particle forward at another +15 m/s, you fully expect that the particle, relative to someone on the ground and at rest, will appear to move at +30 m/s, as 15 + 15 = 30. However, if you were traveling at +150,000,000 m/s and you shot a particle forward at another +150,000,000 m/s, that particle won’t appear to move at +300,000,000 m/s relative to someone at rest; they would only see it moving at about +240,000,000 m/s, as velocities must be added only relativistically, not under the conventional Galilean/Newtonian rules.
In fact, if you accelerated constantly, at 9.8 m/s², toward any distant astronomical object, you’d find that you never quite reached the speed of light, but only approached it from below. You’d find that you still continued to move faster and faster, and that your destination continued to get closer and closer (and also, the light from it would appear more and more blueshifted as you achieved increasingly greater speeds), but that every photon you emitted still:
- moved at the speed of light, relative to you,
- moved at the speed of light, relative to your source and your destination (and everyone else),
- and received only a change in wavelength, not speed, because of your motion when you emitted it.
However, two things would change dramatically for you on your relativistic (i.e., close to the speed of light) journey: the way you experienced both distances and times relative to someone who remained at rest, either at the source, the destination, or at any other point along your journey.
- Distances, rather than being fixed between any two points, would be observed to contract along your direction of motion. This phenomenon of length contraction was named after the scientists George FitzGerald and Hendrik Lorentz, who first understood this even before Einstein’s special relativity came along.
- Time, rather than appearing to pass at the same rate for everyone everywhere, is instead relative, with time being observed to dilate between the space traveler in motion relative to the origin and the destination, where clocks appear to run slower for the observer in motion relative to the stationary ones.
While someone who remained at the same location they started at, such as the origin point or the destination point, would continue to age as normal, someone who traveled through a significant amount of space during that same interval would experience a shorter passage of time, and the amount that it was shorter by would depend entirely on how close they made it to the speed of light during their journey. The faster you go, the less amount of time passes for you, the traveler, but as measured by an observer at either the source or destination, at least as much time that it would take a light ray to travel from here-to-there is required for a spacefaring traveler to traverse the same distance.

Tachyonic motion
Of course, all of this is for normal matter and antimatter: particles that have a real, positive mass. Because of Einstein’s most famous equation, E = mc², we also know that whatever the mass (m) of a particle is just describes a specific form of energy (E) that it possesses: its rest mass energy. There are other forms of energy that can be inherent to a particle (or antiparticle) as well, including, quite famously, kinetic energy, or the energy of motion. In fact, even though we write E = mc² down quickly and easily, and often without much thought, it turns out that’s only half of the equation describing a particle’s energy: the half that applies only if the particle in question is at rest. For a particle in any sort of generic motion, the true equation is as follows:
E = √(m²c⁴ + p²c²),
where E is the energy, m is the rest mass, c is the speed of light, and in the term you don’t normally see written out, p is the particle’s momentum. Normally, for all known particles, its rest mass can either be positive (for things like quarks and antiquarks, neutrinos and antineutrinos, charged leptons and antileptons, etc.) or zero (for massless particles like the photon, gluon, or gravitational waves, whose quantum analogue would be the graviton). But there’s another possibility that could yet exist within this Universe: particles with imaginary mass, where the imaginary number i is defined as √(-1).

If you have an imaginary mass, then the equation E = √(m²c⁴ + p²c²) can give you a negative number if your momentum is low enough; you can have a negative energy state for this hypothetical type of particle, which would be known as a tachyon.
Although tachyons have not been proven to exist, they have an extremely bizarre and counterintuitive property: the more energy you put into a tachyon, the closer and closer it gets to the speed of light, just like for regular matter. Only, for a tachyon, it approaches the speed of light from above, rather than below. In other words, the slowest-moving tachyon and the fastest-moving positive mass particle both approach the same speed that they can never actually achieve, the speed of light.
If you have a positive mass particle and you take more and more of its kinetic energy away, its speed drops, and can drop all the way down to zero if it has no kinetic energy (or momentum) at all. But for a tachyon, i.e., an imaginary mass particle, the more of its kinetic energy you remove, the faster it goes: all the way up to infinite speed for a tachyonic particle with no kinetic energy (or momentum) inherent to it at all. Although there’s no evidence that tachyons can (or do) exist, discovering the ability to manipulate any:
- negative energy state,
- or any imaginary mass state,
would suddenly and definitively allow the possibility of faster-than-light space travel.

General relativistic possibilities
Alright, so maybe you have good reason to think that tachyons don’t exist, and that even though there’s a positive, non-zero amount of energy inherent to the fabric of space itself — dark energy — that you might not be able to physically achieve a true negative energy state, no matter what you do. Does that mean that, if there are no tachyons, that traveling faster than light is truly impossible?
The answer is “not necessarily,” as it only forbids faster than light travel in special, not general, relativity. The key insight of general relativity, remember, is that not only are space and time relative to the observer, but the very underlying fabric of the two stitched together — the fabric of spacetime — is distorted by the distribution of matter-and-energy everywhere throughout space at all moments in time. In the general relativistic picture:
- every mass in the Universe curves the fabric of spacetime,
- every quantum of energy curves the fabric of spacetime,
- the fabric of spacetime isn’t fixed, but can either expand or contract,
- and gravitational waves propagate through spacetime despite having no mass of their own, moving at the speed of light and generated by any massive quantum that moves through a region of changing spacetime curvature.
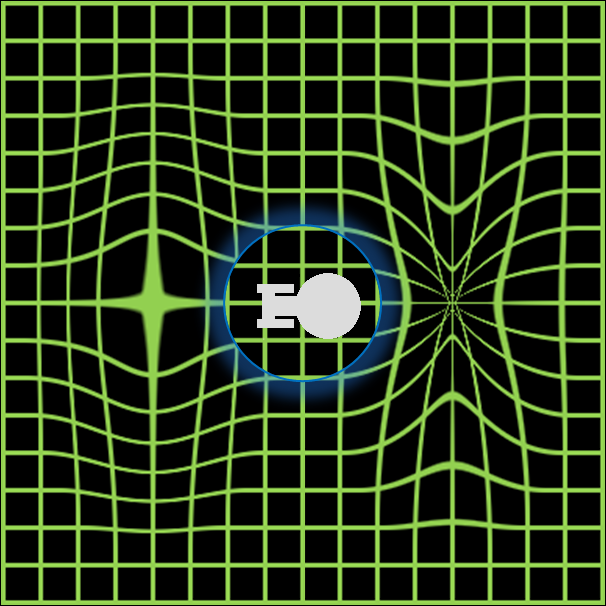
Although most astrophysical objects (such as the stars and planets) in the Universe distort the fabric of spacetime only by a very small amount, there are a few objects that can generate enormous spacetime curvatures, such as black holes.

If spacetime is curved severely enough not just in one location, but in multiple disparate locations, it’s possible to imagine that one region of severe curvature could connect to another, leading to what’s colloquially known as a wormhole, or an Einstein-Rosen bridge. Rather than having to travel across the vast cosmic distances separating these two locations, it could become possible (especially if you can stabilize the wormhole, enabling matter to pass through it without being torn apart by the gravitational tidal forces) to send real material, including an entire spaceship, on a short-cut through a wormhole to go from an origin to a destination faster than even the speed of light would allow by taking the long way.
There are other possibilities for how to travel faster-than-light as well within general relativity. If you had a source of negative energy — not necessarily absolutely negative, as was needed for a tachyon, but just negative relative to the (positive) zero-point energy of empty space — you could use a mix of positive energy (in front of the spaceship) and negative energy (behind the spaceship) to distort the fabric of space in a particular fashion:
- compressing it ahead of the spaceship,
- rarefying (i.e., anti-compressing) it behind the spaceship,
- all while having a stable, non-destructive bubble-like region in between, where a spaceship could exist.
This is a physically plausible mechanism to create arguably the most famous faster-than-light travel idea of them all: Star Trek’s warp drive.
In fact, any source of anti-gravitation would enable us to create a warp drive, or to enable faster-than-light travel via multiple clever mechanisms. Many theorists, perhaps excited by this possibility, had pointed out throughout the 1990s, 2000s, and 2010s that the gravitational behavior of antimatter had never yet been measured; we knew that it behaved as though it had positive inertial mass (the “m” in equations like Newton’s F = ma), but we didn’t know how it behaved gravitationally. After many attempts, the ALPHA-g experiment at CERN’s antimatter factory finally made the critical measurement: antimatter falls down, just the same as normal matter, dashing what may have been our best realistic hope for a warp drive.
If tachyons are impossible, and wormholes are impossible, and warp drive is also impossible, does any hope remain for faster-than-light travel that doesn’t demand some sort of new physics?
There may be one possibility: the possibility of what are known as closed time-like loops in general relativity, which arise in many spacetimes, including (possibly) in the Kerr metric, the spacetime describing realistic, rotating black holes. If you have a closed time-like curve, you can:
- leave a point at an initial moment in time,
- take a journey through space, perhaps even a very long journey through space,
- and arrive not only back at your initial location, but back at the initial moment that you departed as well.
In other words, it would be as though you traveled through a finite amount of space in an infinitesimal (zero) amount of time: something that would absolutely indicate some sort of faster-than-light travel has occurred.
Sure, with today’s known laws of physics and known forms of matter, it’s easy to assume that even an arbitrarily advanced species will be unable to overcome the speed limit set by the Universe itself: the speed of light. However, we have to remember that the modern human enterprise of science, realistically, is only a few hundred years old, with even the basic laws of motion and gravity only uncovered within the last 500 years. After thousands or millions of years, we may look back on our current understanding of the Universe the way modern scientists look back on Aristotelian science: as a quaint stab-in-the-dark that’s occasionally a little bit correct, but that represents an infantile caricature of our most accurate picture of reality.
- Will tachyons be discovered, and will we learn that it’s possible to use them to travel through space faster-than-light after all?
- Will we find an imaginary mass or negative energy state, and will we be able to use such a state to distort the fabric of space to create some sort of warp drive?
- Will we be able to bend space severely enough — or is there a location where it’s naturally bent severely enough — to connect to otherwise seemingly disconnected regions of space, enabling a traversable wormhole?
- Or will we be able to leverage the possibility of closed time-like loops to travel through space and return to our starting point, not only in space, but in time as well?
Unless we can be certain that the answer to all of these questions (as well as other possibilities not addressed here) is no, then we cannot rule out the possibility that advanced enough aliens, and perhaps even humanity in the far-enough future, may someday overcome even the most famous of Einstein’s limits. The speed of light is the limiting speed of all known forms of matter and energy that travel through space in a conventional fashion. If anything beyond that can occur, the possibilities are virtually limitless.
Send in your Ask Ethan questions to startswithabang at gmail dot com!