Ask Ethan #30: Long-term timekeeping
The physics of accurately knowing just how much time has passed.
“While friendship itself has an air of eternity about it, seeming to transcend all natural limits, there is hardly any emotion so utterly at the mercy of time.” -Robert Hugh Benson
It’s the end of the week here at Starts With A Bang, and that means it’s time for another Ask Ethan, where you send in your questions and suggestions and I pick my favorite one to answer. Today’s comes from sci-fi writer A.I. Standfield, who asks:
I am writing a science fiction novel series, I am in the world building stage and I wanted to incorporate something. Solar system centric time keeping.
I would love to hear your thoughts on this, and maybe generate discussion on this and other topics.
As it turns out, astrophysical systems can serve as excellent, natural clocks.
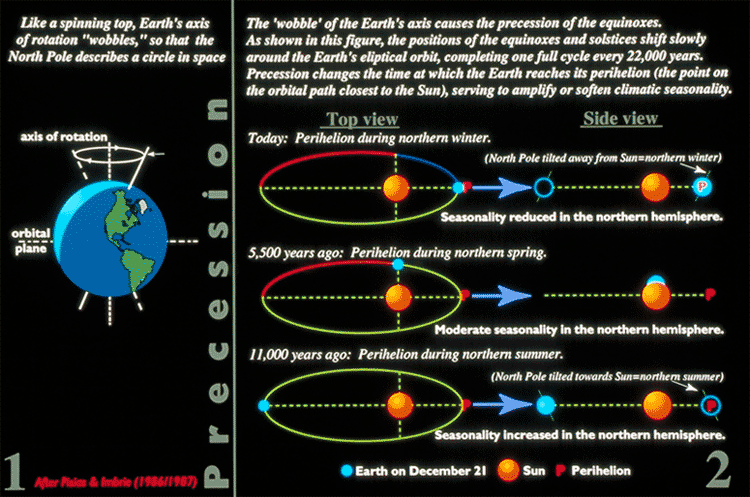
That’s exactly what we use here on Earth, after all! The daily rotation of our planet literally defines our day, while the revolution of the Earth in its orbit around the Sun defines a year. Well, kind of. You see, technically, the Earth orbiting the Sun defines what we call a sidereal year, or the amount of time it take the Earth, Sun and (very distant) fixed stars to return to the same relative positions to one another. But our calendar is based on the tropical year, or the time it takes to go from vernal equinox to vernal equinox.
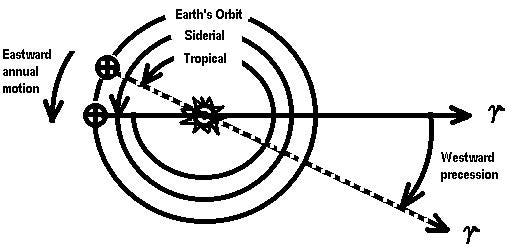
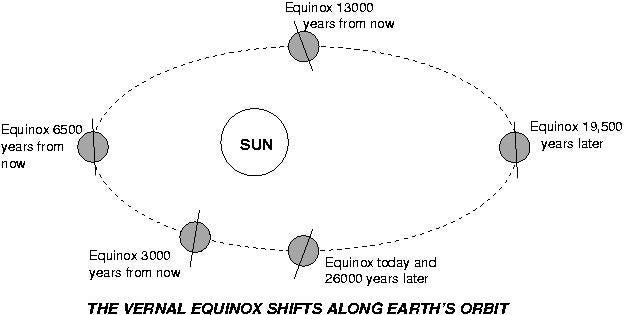
These two definitions of year are almost identical — they differ by just 0.07% from one another — but if we ignored this difference of about 6 hours and 9 minutes per year, our seasons would become the opposite of what they are today every 700 years or so. As it is, we just get a little bit of precession-of-the-equinoxes as time goes on.
If you wanted to do long-term timekeeping, however, you’d do well to forget about tropical years altogether, and days along with them. You see, you hardly notice it from year-to-year, but the rotation of the Earth (and all planets) gradually spin down as the torque exerted by the other gravitational masses in our Solar System interact with us. The fact that we have our Moon exacerbates this effect tremendously, as days on Earth lasted a mere six-to-eight hours some four billion years ago, and in just another four million years, we’ll have no need for (tropical) leap years any longer.
So we could stick to measuring how long it takes our planet to make a single, astronomical orbit. But why pick the Earth?
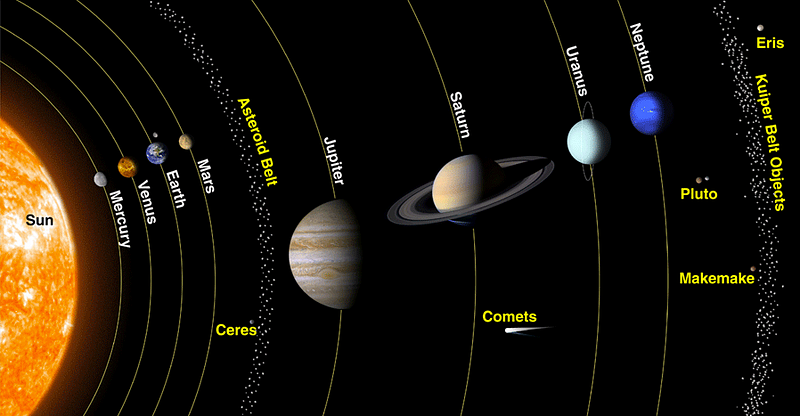
We have eight planets to choose from, and their orbits are curiously patterned as follows:
- Mercury: 0.241 Earth-years (just under 1/4th an Earth-year)
- Venus: 0.615 Earth-years (just about 5/8ths an Earth-year)
- Earth: 1 Earth-year
- Mars: 1.88 Earth-years (almost exactly 3 Venus-years)
- Jupiter: 11.8 Earth-years, most dominant planet in the Solar System
- Saturn: 29.5 Earth-years (almost exactly 2.5 Jupiter-years)
- Uranus: 84 Earth-years (a little under 3 Saturn-years)
- Neptune: 165 Earth-years (almost exactly 2 Uranus-years)
At this stage in the Solar System’s lifetime, these numbers aren’t going to change very much, but they’re not as precisely known as we’d like. The outermost planets, in particular, are only known to 2 or 3 significant digits! But Solar System-centric time has its limits, in terms of precision, consistency and longevity. As it turns out, naturally, the Universe has much better clocks than anything our Solar System has to offer.

Pulsars — in particular, millisecond pulsars — are the best natural clocks in the known Universe. These are collapsed stars that went supernova a long time ago, and left behind a neutron star at their core. Over billions of years, they have spun up to their very fast rotational speed, making a complete revolution every 1-to-10 milliseconds (and remember, these are objects as massive as our Sun) and shooting radio “jets” out of their poles as they rotate.
Each time that jet points towards our line-of-sight, we receive a “pulse” of radio emissions, and hence the name pulsar. The fastest ones live many billions of years (at least), and the record-holder spins more than 700 times per second.
These are also the most accurate clocks we’ve ever discovered. They are so regular that we could watch one, look away for a year, and know — when we look back — whether ten billion pulses have gone by… or whether it’s ten billion-and-one. In fact, we can get down to around microsecond accuracy to their timing over periods of many decades, meaning we can get timing accuracy to around one part in 10^15!
This is bettered only by the most advanced atomic clocks on Earth, and considering that these millisecond pulsars will live billions of years, it’s hard to do better. But at some point, even the millisecond pulsars will die out; what if you wanted to keep time for longer than that? I’ve got an answer for you.

Use Bismuth. Did you ever have a periodic table? When I was a kid, I had one, and I remember Bismuth in particular — element 83 — because it was the heaviest element that was completely stable against radioactive decay. All other elements heavier than Bismuth would eventually decay into lighter elements, having no indefinitely stable isotopes.
Some lasted only seconds or fractions-of-a-second, some lasted days, years, thousands of years, millions or even billions of years. But Bismuth was the heaviest one that was truly stable.
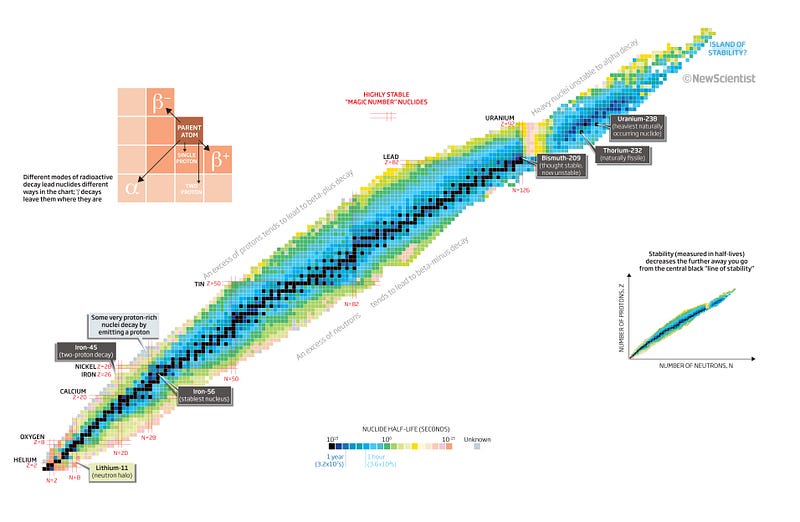
Bismuth-209 is the longest-lived unstable, naturally-occurring element known to humanity, with a half-life of about 1.9 × 10^19 years, or more than a billion times longer than the age of the Universe!
So if you want to know how much time has passed to arbitrary accuracy, all you need is an arbitrary number of bismuth-209 atoms.
- Count them.
- Then wait for time to pass, as much time as you like.
- Then count them again.
If you understand how radioactive decay works, you can calculate how much time has passed! Now, this will take a while; in 2010, the world mined about 8,900 tonnes of Bismuth-209. The current age of the Universe is 13.8 billion years, and if we took that amount of Bismuth-209 and waited another 13.8 billion years, we’d have 8,899,999.9955 kilograms of it still remaining. And this will be limited only by the precision to which you can measure your element’s half-life and the number of atoms you have.
But you can do one better, if you plan on being around even longer.

Tellurium-128 is an unstable isotope of the 52nd element in the periodic table, and it has a half-life of 2.2 × 10^24 years, the longest-lived unstable isotope of them all. It’s possible that there are even longer-lived ones out there — maybe even lead is unstable, after all — and the Universe simply hasn’t been around long enough to find out.
But if I wanted to keep track of time, the Solar System is okay, but for astrophysical objects, millisecond pulsars would be far better. And if you’re taking a journey somewhere, bring some unstable atoms with you, and this way — so long as you can count and do some math — you’ll know precisely how long it’s been. Just bring the right elements with the right half-lives with you, and then you’ll know. And that’s how to keep time for as long as you want!
Have a question you’d like to see on Ask Ethan? Ask away! And if you have a comment on this post, visit the Starts With A Bang forum on Scienceblogs.