Could the expanding Universe truly be a mirage?

Back in the 1920s, two side-by-side developments occurred that paved the way for our modern understanding of the Universe. On the theoretical side, we were able to derive that if you obeyed the laws of General Relativity and had a Universe that was (on average) uniformly filled with matter-and-energy, your Universe couldn’t be static and stable, but must either expand or collapse. On the observational side, we began to identify galaxies beyond the Milky Way, and quickly determined that (on average) the farther away they were observed to be, the faster they were observed to be receding from us.

Simply by putting theory and observation together, the notion of the expanding Universe was born, and has been with us ever since. Our standard model of cosmology — including the Big Bang, cosmic inflation, the formation of cosmic structure, and dark matter and dark energy — is all built upon the basic foundation of the expanding Universe.

But is the expanding Universe an absolute necessity, or is there a way around it? In an interesting new paper that’s recently gotten some publicity, theoretical physicist Lucas Lombriser argues that the expanding Universe can be “transformed away” by manipulating the equations of General Relativity. In his scenario, the observed cosmic expansion would merely be a mirage. But does this stand up to the science we already know? Let’s investigate.

Through the vacuum of space, all light, regardless of wavelength or energy, travels at the same speed: the speed of light in a vacuum. When we observe light from a distant star, we are observing light that has already completed that journey from the source to the observer.

Every once in a while, we recognize that there are multiple different ways to look at the same phenomenon. If these two ways are physically equivalent, then we understand there’s no difference between them, and which one you choose is simply a matter of personal preference.

• In the science of optics, for example, you can either describe light as a wave (as Huygens did) or as a ray (as Newton did), and under most experimental circumstances, the two descriptions make identical predictions.
• In the science of quantum physics, where quantum operators act on quantum wavefunctions, you can either describe particles with a wavefunction that evolves and with unchanging quantum operators, or you can keep the particles unchanging and simply have the quantum operators evolve.
• Or, as is often the case in Einstein’s relativity, you can imagine that two observers have clocks: one on the ground and one on a moving train. You can describe this equally well by two different scenarios: having the ground be “at rest” and watching the train experience the effects of time dilation and length contraction as it’s in motion, or having the train be “at rest” and watching the observer on the ground experience time dilation and length contraction.

As the very word “relative” implies, these scenarios, if they give identical predictions to one another, then either one is just as equally valid as the other.

One revolutionary aspect of relativistic motion, put forth by Einstein but previously built up by Lorentz, Fitzgerald, and others, is that rapidly moving objects appear to contract in space and dilate in time. The faster you move relative to someone at rest, the greater your lengths appear to be contracted, while the more time appears to dilate for the outside world. This picture, of relativistic mechanics, replaced the old Newtonian view of classical mechanics, but also carries tremendous implications for theories that aren’t relativistically invariant, like Newtonian gravity.

The latter scenario, in relativity, suggests to us that we might be interested in performing what mathematicians refer to as a coordinate transformation. You’re probably used to thinking of coordinates the same way René Descartes did some ~400 years ago: as a grid, where all the directions/dimensions are perpendicular to one another and have the same length scales applying equally to all axes. You probably even learned about these coordinates in math class in school: Cartesian coordinates.

But Cartesian coordinates aren’t the only ones that are useful. If you’re dealing with something that has what we call axial symmetry (symmetry about one axis), you might prefer cylindrical coordinates. If you’re dealing with something that’s the same in all directions around a center, it might make more sense to use spherical coordinates. And if you’re dealing not only with space but with spacetime — where the “time” dimension behaves in a fundamentally different way from the “space” dimensions — you’re going to have a much better time if you use hyperbolic coordinates to relate space and time to one another.

What’s great about coordinates is this: they’re just a choice. As long as you don’t change the underlying physics behind a system, you’re absolutely free to work in whatever coordinate system you prefer to describe whatever it is that you’re considering within the Universe.

Once you cross the threshold to form a black hole, everything inside the event horizon crunches down to a singularity that is, at most, one-dimensional. No 3D structures can survive intact. That’s the conventional wisdom, and has been treated as proven for over 50 years. But with rotation added into the mix, one of the assumptions of the “proof” seems to fall apart.

There’s an obvious way to try to apply this to the expanding Universe. Conventionally, we take note of the fact that distances in bound systems, like atomic nuclei, atoms, molecules, planets, or even star systems and galaxies, don’t change over time; we can use them as a “ruler” to measure distances equally well at any given moment. When we apply that to the Universe as a whole, because we see distant (unbound) galaxies receding away from one another, we conclude that the Universe is expanding, and work to map out how the expansion rate has changed over time.

So, why not do the obvious thing and flip those coordinates around: to keep the distances between (unbound) galaxies in the Universe fixed, and simply have our “rulers” and all other bound structures shrink with time?

It might seem like a frivolous choice to make, but oftentimes, in science, just by changing the way we look at a problem, we can uncover some features about it that were obscure in the old perspective, but become clear in the new one. It makes us wonder — and this is what Lombriser explored in his new paper — just what we’d conclude about some of the biggest puzzles of all if we adopted this alternative perspective?

This snippet from a structure-formation simulation, with the expansion of the Universe scaled out, represents billions of years of gravitational growth in a dark matter-rich Universe. Over time, overdense clumps of matter grow richer and more massive, growing into galaxies, groups, and clusters of galaxies, while the less dense regions than average preferentially give up their matter to the denser surrounding areas.

So instead of the standard way of viewing cosmology, you can instead formulate your Universe as static and non-expanding, at the expense of having:

• masses,
• lengths,
• and timescales,

all change and evolve. Because the goal is to keep the structure of the Universe constant, you can’t have expanding, curved space that has growing density imperfections within it, and so those evolutionary effects need to be encoded elsewhere. Mass scales would have to evolve across spacetime, as would distance scales and timescales. They would have to all coevolve together in precisely such a way that, when you put them together to describe the Universe, they added up to the “reverse” of our standard interpretation.

Alternatively, you can keep both the structure of the Universe constant as well as mass scales, length scales, and timescales, but at the expense of having the fundamental constants within your Universe coevolve together in such a way that all of the dynamics of the Universe get encoded onto them.

You might try to argue against either of these formulations, as our conventional perspective makes more intuitive sense. But, as we mentioned earlier, if the mathematics is identical and there are no observable differences between the predictions that either perspective makes, then they all have equal validity when we try to apply them to the Universe.

A variety of energy levels and selection rules for electron transitions in an iron atom. Although many quantum systems can be controlled to lead to extremely energy-efficient transfers, there are no biological systems that work in the same fashion.

Want to explain cosmic redshift? You can in this new picture, but in a different way. In the standard picture:

• an atom undergoes an atomic transition,
• emits a photon of a particular wavelength,
• that photon travels through the expanding Universe, which causes it to redshift as it travels,
• and then, when the observer receives it, it now has a longer wavelength than the same atomic transition has in the observer’s laboratory.

But the only observation that we can make occurs in the laboratory: where we can measure the observed wavelength of the received photon and compare it to the wavelength of a laboratory photon.

It could also be occurring because the mass of the electron is evolving, or because Planck’s constant (ℏ) is evolving, or because the (dimensionless) fine-structure constant (or some other combination of constants) is evolving. What we measure as a redshift could be due to a variety of different factors, all of which are indistinguishable from one another when you measure that distant photon’s redshift. It’s worth noting that this reformulation, if extended properly, would give the same type of redshift for gravitational waves, too.

As a balloon inflates, any coins glued to its surface will appear to recede away from one another, with ‘more distant’ coins receding more rapidly than the less distant ones. Any light will redshift, as its wavelength ‘stretches’ to longer values as the balloon’s fabric expands. This visualization solidly explains cosmological redshift within the context of the expanding Universe. If the Universe is expanding today, that means it was smaller, hotter, and denser in the past: leading to the picture of the hot Big Bang. It also explains why all quanta lose kinetic energy as the Universe expands.

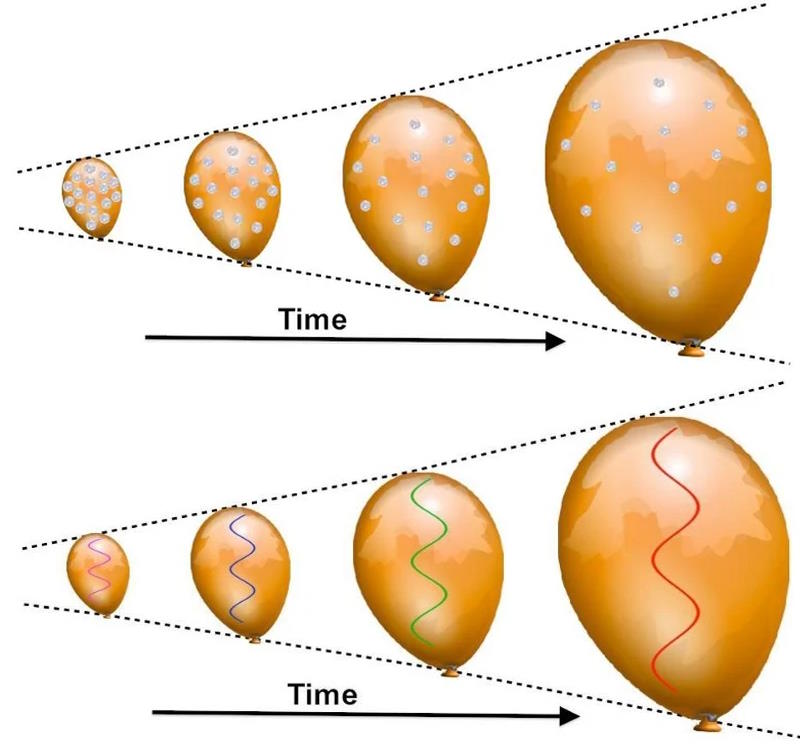
Similarly, we could reformulate how structure grows in the Universe. Normally, in the standard picture, we start out with a slightly overdense region of space: where the density in this region is just slightly above the cosmic mean. Then, over time:

• this gravitational perturbation preferentially attracts more matter to it than the surrounding regions,
• causing space in that region to expand more slowly than the cosmic average,
• and as the density grows, it eventually crosses a critical threshold triggering conditions where it’s gravitationally bound,
• and then it begins gravitationally contracting, where it grows into a piece of cosmic structure like a star cluster, galaxy, or even larger collection of galaxies.

However, instead of following the evolution of a cosmic overdensity, or of the density field in some sense, you can replace that with a combination of mass scales, distance scales, and time scales evolving instead. (Similarly, Planck’s constant, the speed of light, and the gravitational constant could evolve, alternatively, instead.) What we see as a “growing cosmic structure” could be a result not of cosmic growth, but of these parameters fundamentally changing over time, leaving the observables (like structures and their observed sizes) unchanged.

Regions born with a typical, or “normal” overdensity, will grow to have rich structures in them, while underdense “void” regions will have less structure. However, early, small-scale structure is dominated by the most highly peaked regions in density (labeled “rarepeak” here), which grow the largest the fastest, and are only visible in detail to the highest resolution simulations.

If you take this approach, however unpalatable it may seem, you can try to reinterpret some of the presently inexplicable properties our Universe seems to possess. For example, there’s the “cosmological constant” problem, where for some reason, the Universe behaves as though it were filled with a field of constant energy density inherent to space: an energy density that doesn’t dilute or change in value as the Universe expands. This wasn’t important long ago, but appears to be important now only because the matter density has diluted below a certain critical threshold. We don’t know why space should have this non-zero energy density, or why it should take on the value that’s consistent with our observed dark energy. In the standard picture, it’s just an unexplained mystery.

However, in this reformulated approach, there’s a relationship between the value of the cosmological constant and — if you have mass scales and distance scales changing according to the new formulation — the inverse of the Planck length squared. Sure, the Planck length changes as the Universe evolves in this new formulation, but it evolves biased toward the observer: the value we observe now has the value that it has now simply because it is now. If times, masses, and lengths all evolve together, then that eliminates what we call the “coincidence problem” in cosmology. Any observer will observe their effective cosmological constant to be important “now” because their “now” keeps evolving with cosmic time.

An illustration of how the radiation (red), neutrino (dashed), matter (blue), and dark energy (dotted) densities change over time. In a new model proposed some years ago, dark energy would be replaced by the solid black curve, which is heretofore indistinguishable, observationally, from the dark energy we presume. As of 2023 in an expanding Universe, dark energy can deviate from a “constant” by about ~7% in the equation of state; any more is too tightly constrained by the data.

They can reinterpret dark matter as a geometric effect of particle masses increasing in a converging fashion at early times. They can alternately reinterpret dark energy as a geometric effect as particle masses, at late times, increase in a diverging fashion. And, quite excitingly, there may be ties between a different way to reinterpret dark matter — where cosmic expansion is reformulated as a scalar field that winds up behaving like a known dark matter candidate, the axion — and couplings between the field causing expansion and the matter in our Universe introduces CP violation: one of the key ingredients needed to generate a matter-antimatter asymmetry in our Universe.

Thinking about the problem in this fashion leads to a number of interesting potential consequences, and in this early “sandbox” phase, we shouldn’t discourage anyone from doing precisely this type of mathematical exploration. Thoughts like this may someday be a part of whatever theoretical foundation takes us beyond the well-established current standard picture of cosmology.

However, there’s a reason that most modern cosmologists who deal with the physical Universe we inhabit don’t bother with these considerations, which are interesting from the perspective of pure General Relativity: the laboratory also exists, and while these reformulations are okay on a cosmic scale, they conflict wholeheartedly with what we observe here on Earth.

When a hydrogen atom forms, it has equal probability of having the electron’s and proton’s spins be aligned and anti-aligned. If they’re anti-aligned, no further transitions will occur, but if they’re aligned, they can quantum tunnel into that lower energy state, emitting a photon of a very specific wavelength (21 cm) on very specific, and rather long, timescales. The precision of this transition has been measured to better than 1-part-in-a-trillion, and has not varied over the many decades it’s been known. It is the first light emitted in the Universe after the formation of neutral atoms: even before the formation of the first stars, but also thereafter: whenever new stars are formed, ultraviolet emission ionizes hydrogen atoms, creating this signature once again when those atoms spontaneously re-form.

Consider, for example, the notion that either:

• fundamental particle properties, such as masses, charges, lengths, or durations are changing,
• or fundamental constants, such as the speed of light, Planck’s constant, or the gravitational constant are changing.

Our Universe, observably, is only 13.8 billion years old. We’ve been making high-precision measurements of quantum systems in the lab for several decades now, with the best-precision measurements revealing properties of matter to within about 1.3 parts in ten trillion. If either the particle properties or the fundamental constants were changing, then our laboratory measurements would be changing as well: according to these reformulations, over a ~14 year timescale (since 2009 or so), we would have noticed variations in the observed properties of these well-measured quanta that are thousands of times larger than our tightest constraints: of about 1-part-per-billion.

• The electron magnetic moment, for example, was measured to very high precision in 2007 and in 2022, and showed less than a 1-part-in-a-trillion variation (the limits of the earlier measurement’s precision) between them, showing that the fine-structure constant hasn’t changed.
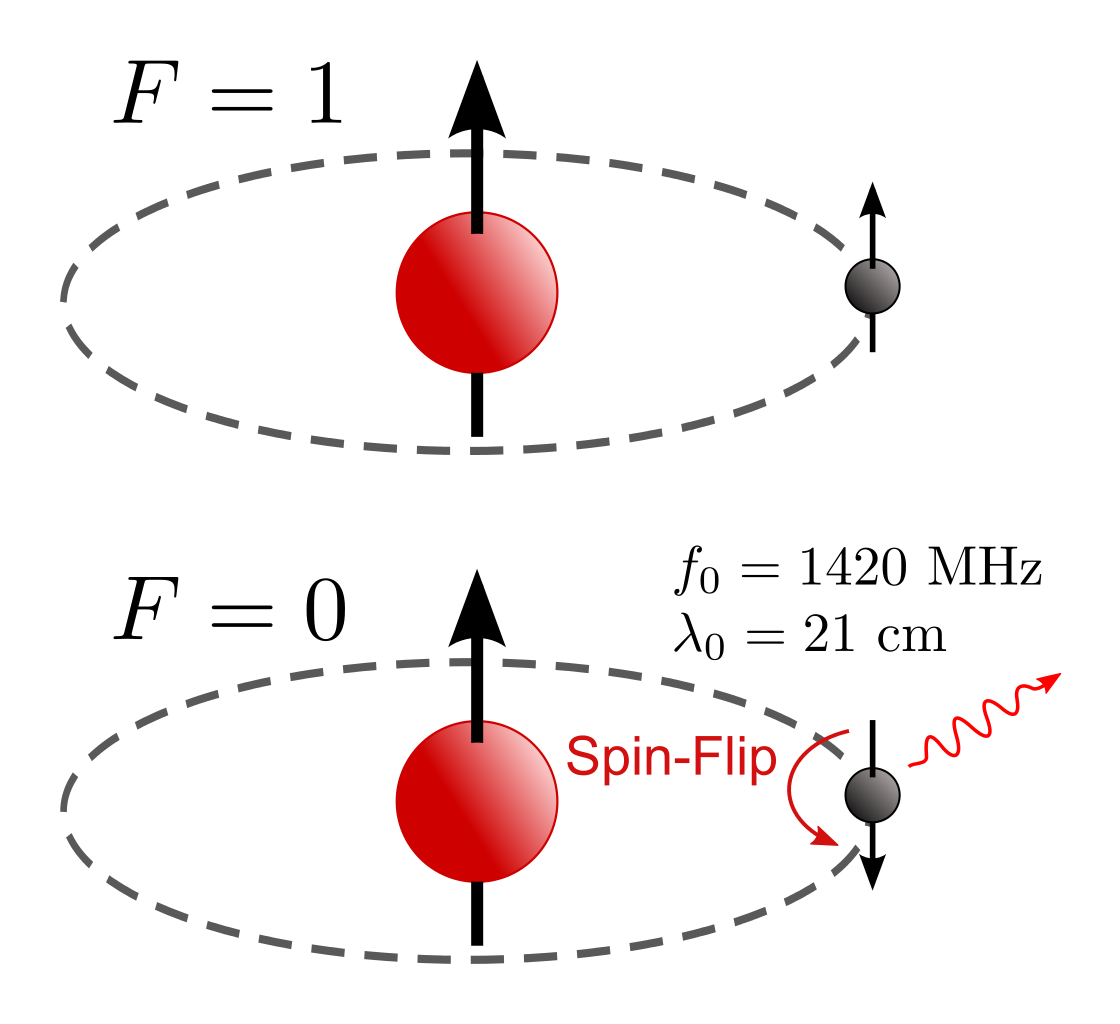
• The spin-flip transition of hydrogen, which results in an emission line of a precise wavelength of 21.10611405416 centimeters, has an uncertainty on it of just 1.4 parts-per-trillion and has not changed since it was first observed in 1951. (Although we’ve measured it better over time.) That shows Planck’s constant hasn’t changed.
• And the Eötvös experiment, which measures the equivalence of inertial mass (which isn’t affected by the gravitational constant) and gravitational mass (which is) has shown these two “types” of mass are equivalent to a remarkable 1-part-per-quadrillion as of 2017.

The equivalence principle holds that there should be no difference between a gravitational acceleration and an acceleration due to any other force in the Universe. Since one is dependent on the gravitational constant and the other is not, testing the equivalence principle, done most precisely by the MICROSCOPE satellite to 1 part in 10^15, is a way to constrain time variations in the gravitational constant. The equivalence principle, as originally formulated by Einstein, was the single idea that he referred to as his “happiest thought” in life.

This is a remarkable feature about our Universe under the standard way of looking at things: the very same laws of physics that apply here on Earth apply everywhere else in the Universe, at all locations and times throughout our cosmic history. A perspective applied to the Universe that fails here on Earth is far less interesting than one that applies successfully over the full range of physically interesting systems. If the conventional expanding Universe also agrees with physics on Earth and an alternative to it describes the larger Universe well but fails here on Earth, we cannot say the expanding Universe is a mirage. After all, physics here on Earth is the most real and most well-measured and well-tested anchor we have for determining what’s actually real.

That isn’t to say that journals that publish this type of speculative research — Classical and Quantum Gravity, the Journal of High-Energy Physics, or the Journal of Cosmology and Astroparticle Physics, to name a few — aren’t reputable and high-quality; they are. They’re just niche journals: far more interested in these types of early-stage explorations than they are with a confrontation with our experimentally and observationally driven reality. By all means, keep playing in the sandbox and exploring alternatives to the standard cosmological (and particle physics) pictures of reality. But don’t pretend that throwing out all of reality is a viable option. The only “mirage” here is the notion that our observed, measured reality is somehow unimportant when it comes to understanding our Universe.