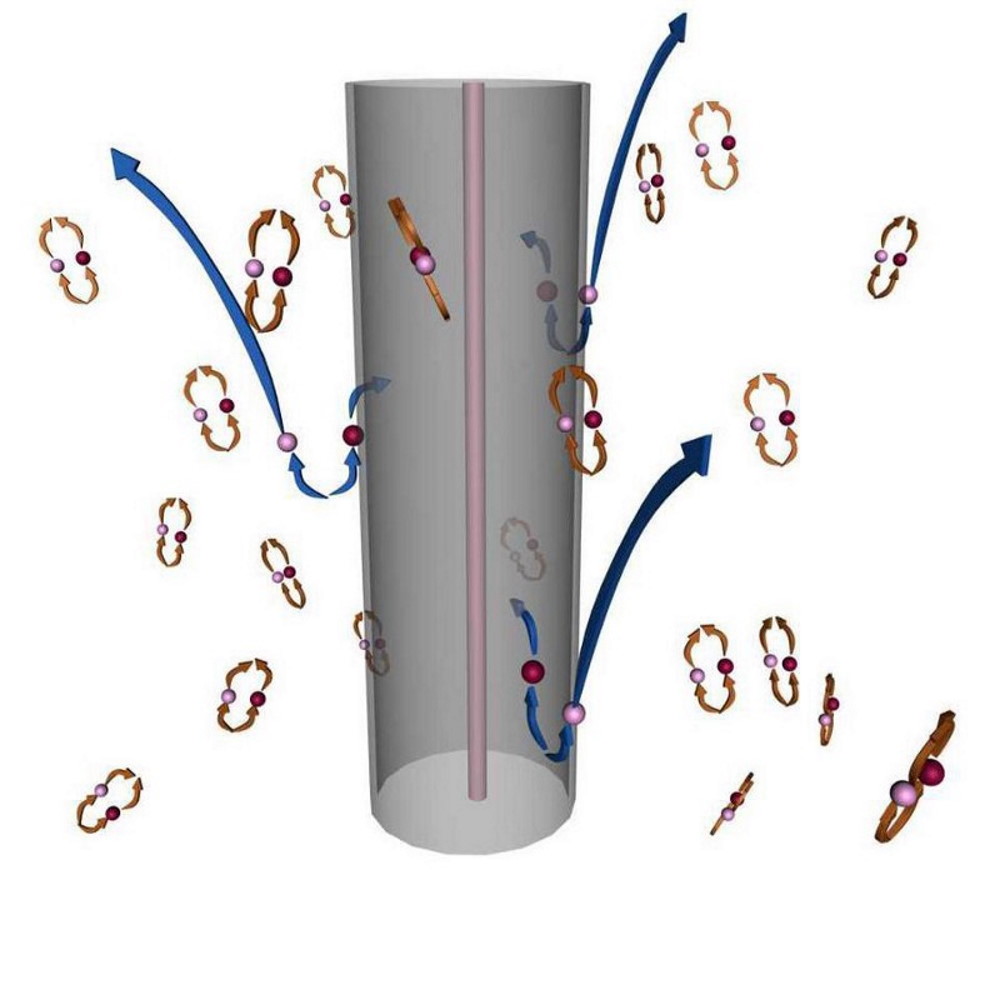
Ask Ethan: How does Hawking radiation really work?

- Hawking radiation is one of the most incredible phenomena in the Universe, which will eventually lead to the complete decay and evaporation of the most gravitationally profound objects of all: black holes.
- According to no less an authority than Stephen Hawking himself, this operates based on particle-antiparticle pairs spontaneously being created by the quantum vacuum, where some members escape, leading to evaporation.
- But Hawking’s explanation isn’t just misleading, it’s completely incorrect. Black holes don’t emit matter or antimatter via Hawking radiation, but low-energy photons. Here’s how they really evaporate.
For many good reasons, black holes are among the most studied objects in the entire Universe. Initially predicted back in the late 18th century in the context of Newtonian gravity, black holes were shown to arise in the context of general relativity as early as 1916. Astrophysically, they can be formed when gas clouds collapse, when the cores of stars implode, or when two neutron stars collide, among other mechanisms. They have been observed via numerous methods: from electromagnetic emissions that arise from matter around them, from the motion of stars or binary companions around them, and from the gravitational waves they emit when two of them merge together.
But perhaps, most remarkably of all, it was shown in the early 1970s that black holes cannot endure forever, but will eventually evaporate due to the continuous spontaneous emission of radiation that emerges from them: Hawking radiation. But how does Hawking radiation truly work? Not as Hawking asserted, unfortunately, which brings us to the question submitted by Leif Koesling:
“Earlier today I was reading your article on Hawking Radiation and was very confused with your explanation.
You mentioned that this particle and antiparticle cancellation was not in fact true, and that it was actually the curvature gradient of the black hole that was creating this Radiation.
Could you maybe explain this? How can the bending of spacetime result in Radiation?”
There’s a lot to consider, but let’s try to make it as clear as possible by beginning from an unusual starting point: empty space.

Most of us, initially, think of empty space as some sort of perfect “emptiness” without anything inside:
- no particles,
- no antiparticles,
- no radiation,
- no fields,
- no curvature of space,
- and no energy of any type at all.
We think of it as some sort of void, where nothing exists within it. Although that’s something that makes intuitive sense from an a priori point of view, it turns out that’s not quite right at all from a physical perspective.
You see, even in space that’s as empty as you can possibly imagine it — say, in deep intergalactic space, hundreds of millions of light-years away from any sources of matter, with an enormous “shield” around a large volume of it to keep everything out — you still can’t eliminate everything. You might be able to keep external electromagnetic fields from getting in, and you might be able to expel all particles, antiparticles, and radiation. But you can’t extricate space itself from the laws of physics, and that means that the fundamental quantum fields that are inherent to the Universe itself will still exist. They might be in what we call the “ground state” (or lowest-energy state), with zero excitations to that state, but those underlying fields still remain a part of reality.

It’s also important to recognize that these fields — which are the “carriers” of all of the fundamental forces — persist throughout all of space, regardless of whether there are sources (quanta) present in that space or not. Traditionally, we then invoke the Heisenberg uncertainty principle, noting that there are pairs of quantum properties that cannot be exactly measured or known together, such as:
- position and momentum,
- energy and time,
- spin in mutually perpendicular directions,
as well as many others. The idea that people then run with is that, if you consider a short enough timescale (Δt), then there will be a large associated energy (ΔE) that goes along with it, and if that associated energy (ΔE) is large enough, then via mass-energy equivalence (i.e., Einstein’s E = mc²), you can create a particle-antiparticle pair of quantum particles, spontaneously, from nothing. Once too much time elapses, those pairs find each other again and re-annihilate, and go back into nothingness, where nothingness means the quantum vacuum of empty space.
This oversimplified picture, despite its widespread use, is completely wrong. The idea that the zero-point energy of empty space comes from this “particle-antiparticle popping” is a complete work of fiction.
So what is happening, realistically, instead?
There really is what we call zero-point energy, or a value of energy that is inherent to the ground state of any quantum system, and it is often positive and non-zero. But it doesn’t arise from “quantum fluctuations” or “quantum foam” or “particle-antiparticle pair popping” or any other name you give to it. Instead, it comes from what we call the free Hamiltonian (the operator associated with the total energy of a non-interacting system), which represents a series of non-interacting quanta just “sitting there,” oscillating and propagating, but not interacting with any other.
There really are quantum fields permeating all of space, and there’s no way to create a region devoid of them. Similarly, you can be as far away as you like from all sources of matter and energy in the Universe, but that doesn’t necessarily mean that you’ll wind up living in perfectly flat space; as long as you live in a Universe that’s expanding and/or that has any sources of matter and/or energy anywhere within it, you can only approximate space as being flat and uncurved; in reality, there is some quantifiable, even if small, curvature to it.

Even so, we can imagine completely flat-and-empty space, but instead of also imagining that we’re stationary within it, imagine that we’re accelerating through it, instead. Remember that the key principle of relativity is not that “all observers have equal claims to their frame-of-reference being the correct, preferred one,” but rather that this only applies to inertial, or non-accelerating, frames-of-reference. If you’re in a rocket and accelerating through even flat, empty space, that means you’re in a non-inertial frame-of-reference, and your traditional thought of “my frame is just as good as anyone else’s” is now no longer true.
In flat, empty space, if you’re not accelerating, you will simply experience an empty Universe with no quanta of matter or radiation appearing in any direction. However, if you are accelerating, you’re going to experience a non-inertial effect known as the Unruh effect (or Fulling-Davies-Unruh effect): where you will perceive a thermal bath of radiation, whose temperature depends on the magnitude of your (uniform) acceleration. The reason comes from the different state of the quantum vacuum that a stationary observer perceives, where all of the quantum fields are in their lowest-energy (ground) state, as compared with an accelerating observer, where some of the particles need to be in a “boosted” energy state to correspond to thermal equilibrium, which occurs at a higher temperature than the ground-state for a non-accelerating observer.

So, let’s recap where we’ve gotten to so far, as background.
- Empty space isn’t empty, but possesses quantum fields everywhere.
- We shouldn’t view these quantum fields as “particle-antiparticle pairs popping in-and-out of existence,” which is a false temptation, but rather as an ensemble of non-interacting particles in the ground state.
- If you are stationary and not accelerating in flat, empty space where these quantum fields exist, you will see the vacuum as corresponding to this ground state, and you will see no radiation emerging from anywhere.
- But if you are uniformly accelerating, even through flat, empty space, you will effectively “boost” the energy of the ground state, and that will lead to a thermal bath of radiation.
In fact, it’s pretty straightforward to calculate what that temperature is going to be: ħa/2πckB, where:
- ħ is Planck’s constant,
- a is the magnitude of the acceleration,
- 2 and π are numerical constants,
- c is the speed of light in a vacuum,
- and kB is Boltzmann’s constant.
This normally corresponds to tiny temperatures; if you accelerated at 1g, for example, or the acceleration of gravity at Earth’s surface, the Unruh temperature of your radiation is going to be about 4 × 10-20 K, or about a billion times smaller than the coldest laboratory temperature ever achieved.
Now, we’re going to take a huge leap, and go from flat space into the curved space of general relativity, and we’re going to do it the same way Einstein did it: by invoking what’s known as the equivalence principle.
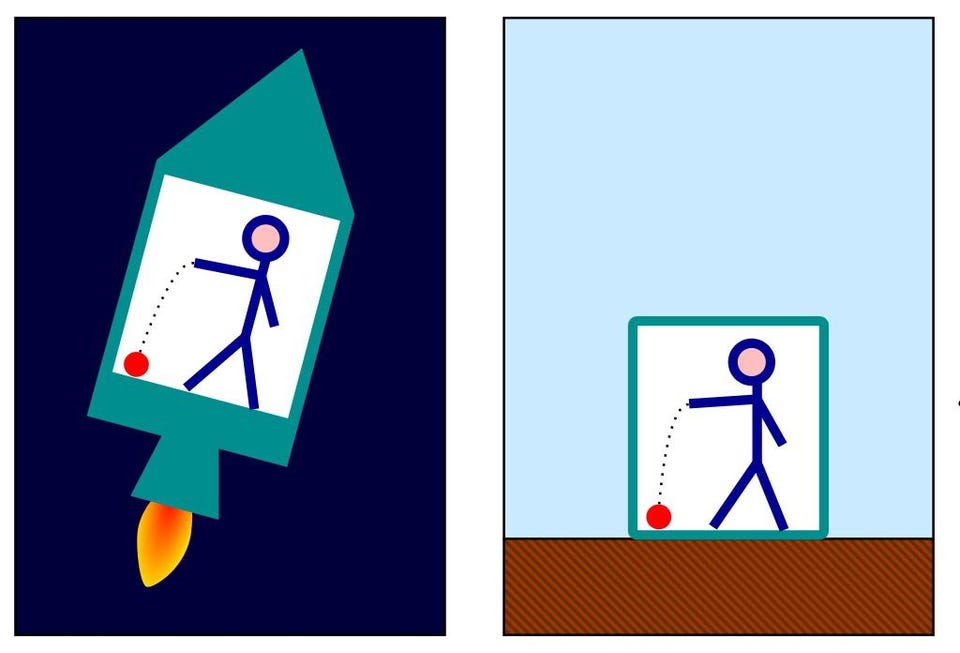
The equivalence principle is what Einstein, upon realizing it in 1908, referred to throughout his entire life as his “happiest thought.” He imagined an observer in a room that was uniformly accelerating upward, such as an elevator being pulled up or otherwise propelled through space. (Rocketry eluded Einstein’s imagination, as the first rocket wasn’t invented until 1926.) Then he imagined that same room at rest on the surface of Earth: where the force of gravity pulls it down. What would be the difference, experimentally, between the experience of someone in each of the two rooms who dropped a ball directly downward?
Nothing.
The two situations would be physically identical, and that was the key insight that led Einstein, over the next 7 years or so, to formulate his general theory of relativity, which superseded Newtonian gravity and is still our leading theory of gravitation today. So if Unruh radiation arises, even in empty space, by the way the quantum vacuum transforms when we accelerate through it, then what happens if we replace the “acceleration” we talked about earlier with a source of gravitation, such as a black hole? All we have to do is look at how space flows, which tells us how any observer would be compelled to accelerate as they were “dragged” through space by the presence of that source of gravitation.

The closer you get to a black hole, the faster you accelerate. The more massive a black hole is, the greater the amount that it distorts space, and so the larger its acceleration-equivalent becomes. However, the more massive a black hole gets, the larger its event horizon also becomes, and therefore the farther away from the black hole you have to be before you, and everything, get “swallowed” up inside the event horizon. Therefore, you’d imagine the following:
- When you are very far away from a black hole, the total amount of radiation emitted by the black hole will appear very, very small, but still finite, positive, and non-zero.
- As you approach the black hole, you’ll accelerate more and more, and so you expect to see greater and greater amounts of radiation coming from it, peaking as you near the event horizon.
- Since the lowest-mass black holes have the greatest accelerations at their event horizons, you’d expect that low-mass black holes would have higher temperatures (in this case, Hawking temperatures rather than Unruh temperatures) as compared to higher-mass black holes.
- And that, as time went on and black holes emit greater cumulative amounts of energy, then by E = mc², they’ll lose mass, and so over time, black holes will evaporate, with their temperatures and rates-of-evaporation increasing the more mass they lose.

All of this, in fact, is precisely what happens for black holes. They emit not Unruh radiation, but rather Hawking radiation, named for physicist Stephen Hawking. It’s fascinating that if you go back to Hawking’s original paper — which celebrates its 50th anniversary this year, by the way — you will find no mention of particle-antiparticle pairs popping in-and-out of the quantum vacuum, as he only invoked that flawed, even wholly incorrect analogy more than a decade later in his popular book: A Brief History of Time. Arguably, it’s one of the most destructive ideas in all of science communication; despite its popularity, it doesn’t represent reality at all. (You can read this older piece for an instructive takedown of the idea.)
And yet, it’s wholly unnecessary. Perhaps the only big arguments left over Hawking radiation are:
- whether we’ll ever be able to measure it,
- and whether it requires an event horizon to truly exist, or whether all masses create it,
as not only does it exist, but it doesn’t require any flawed analogy to understand. All you need to do is understand Unruh radiation, or the concept that an accelerated observer, even in flat, empty space, will experience time differently than a stationary observer. Because of that, they’ll see a different quantum vacuum than that stationary observer, which will “boost” the energy of the lowest-energy quantum state, leading to a thermal bath of radiation. That applies to any acceleration, whether due to a spacecraft, an elevator, or the presence of a black hole.

We can then extend what we know about Unruh radiation, Hawking radiation, and black hole decay to two fascinating cases that aren’t normally thought of in the same breath: the dark energy-rich expanding Universe and the period of cosmic inflation that set up and preceded the Big Bang.
- The zero-point energy of space is not zero, but has some finite, tiny, positive value, and that is one way to talk about dark energy: as a form of energy inherent to space itself. Because of the presence and properties of dark energy, there will be a continuous amount of thermal radiation emitted from the perspective of any stationary observer. Even arbitrarily far into the future, this implies that the Universe will always be filled with a tiny amount of blackbody radiation, peaking with a minuscule temperature of about ~10-30 K.
- But early on, space was also filled with a form of energy inherent to it, but of a much greater magnitude: during the period of cosmic inflation. Although the energy scale of inflation is not yet known, one can expect much greater temperatures from that much more rapidly expanding phase: something around ~100 K, which would be warm enough to boil liquid nitrogen away. Instead of an event horizon, the expanding Universe creates a cosmological horizon, and hence we can be confident this radiation will be physical and real as well.
As long as spacetime is bent in such a way that objects accelerate through it, that spacetime is going to create radiation, and because the acceleration changes closer to or farther from a source of mass (like a black hole), radiation will propagate from the regions of stronger curvature (closer to the event horizon) to regions of weaker curvature (farther away from the event horizon). It may not be quite as “simple” as Hawking’s oversimplified picture of particle-antiparticle pairs, but at least this explanation is correct!
Send in your Ask Ethan questions to startswithabang at gmail dot com!