The Higgs boson’s most captivating puzzle still remains

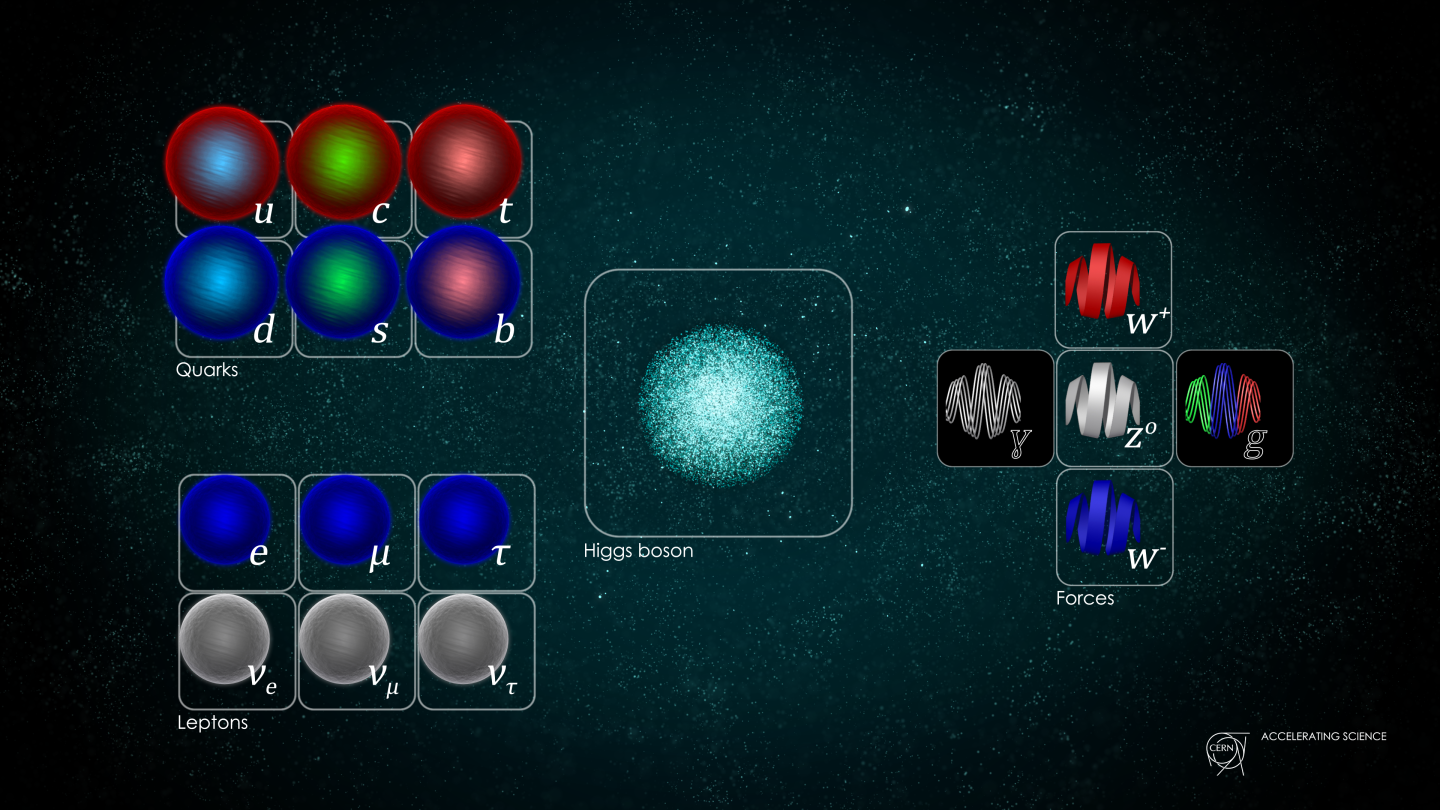
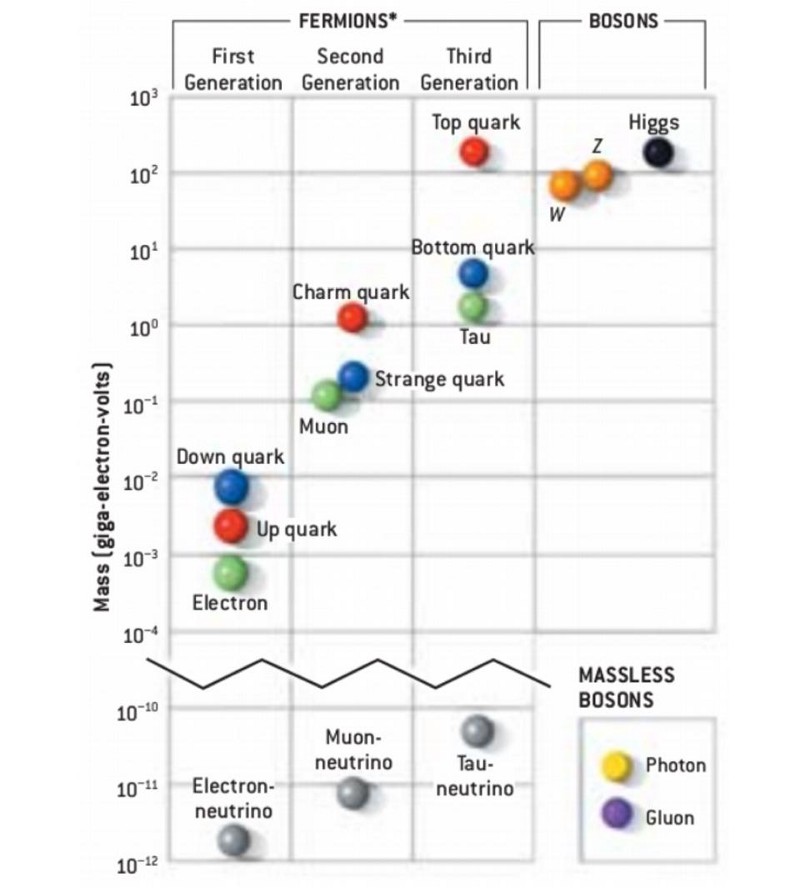
In some ways, the deepest question one can ask about our physical reality is simply, “What is the Universe made of?” In the early 1800s, we thought we knew the answer: atoms. By the early 1900s, the answer had grown much richer: atoms themselves were composed of atomic nuclei and electrons, which were capable of both emitting and absorbing photons: particles of light. However, it was the 1932 discovery of the neutron — along with the puzzle of radioactive beta decay — that would kick off the series of events that led to our modern theoretical picture of particles in the Universe: the Standard Model of elementary particles, including quarks, leptons, and all of the force-carrying bosons.

Even though the last of the undiscovered particles of the Standard Model was finally found in 2012 with the announcement of the Higgs boson, our understanding of what the Universe is made of is still not complete. From a different perspective, we still don’t know:

• what dark matter and dark energy are made of (they’re not any of the Standard Model particles),
• how the events at the end of cosmological inflation gave rise to the hot Big Bang that began the Universe as we know it,
• why the Standard Model particles have the masses and other properties that they do,
• and why the particles that do exist within our Universe are overwhelmingly made of matter and not antimatter.

While the connection might not seem obvious, it’s that last question that scientists studying the Higgs boson might be on the cusp of answering, if only they can obtain the critical data. Here’s why this puzzle is so captivating.

Based on the masses of the top quark and the Higgs boson, we could either live in a region where the quantum vacuum is stable (true vacuum), metastable (false vacuum), or unstable (where it cannot stably remain). The evidence suggests, but does not prove, that we are in a region of false vacuum, which might be a hint that the Standard Model is possibly not all that there is to the Universe of accessible particles.

The problem of beta decay

Inside every atomic nucleus, only two species of composite particle can be found: the proton and neutron. Protons can easily and stably exist on their own, with a mass of 938.272 MeV. They are composed of two up quarks and one down quark, all bound together by gluons. Neutrons, on the other hand, cannot stably exist on their own, but only in three states:

• as a free neutron, which will decay into a proton, electron, and (although it was unknown until decades after the 1930s) an antineutrino,
• as part of a bound nucleus that’s actually stable, where the protons and neutrons are bound together with sufficient energy that the neutrons within the nucleus will not decay,
• or as part of an unstable bound nucleus, where the bound protons-and-neutrons can decay into a more stable state or combinations of states, including decays that also proceed by a single neutron within the nucleus decaying the same way a single, free neutron decays.

The reason for this is that a neutron is not only slightly more massive than a proton, with a rest mass of 939.565 MeV, but slightly more massive than a proton, electron, and antineutrino combined.

So why do neutrons not only decay, but why do their decays take so long: 15 minutes for a free neutron, and anywhere from a fraction-of-a-second to more than billions of years for a neutron-rich nucleus to decay?

This diagram shows how a free neutron (or antineutron) decays at the subatomic level. A down quark (or antiquark) within a neutron (or antineutron), shown on the left in red, emits a virtual W-(or W+) boson, transforming into an up quark (or antiquark). The W-(or W+) boson forms an electron/electron antineutrino (or positron/electron neutrino) pair, while the up quark (or antiquark) recombines with the original remnant up-and-down quarks (or antiquarks) to form a proton (or antiproton). This is the process behind all beta decays in the Universe.

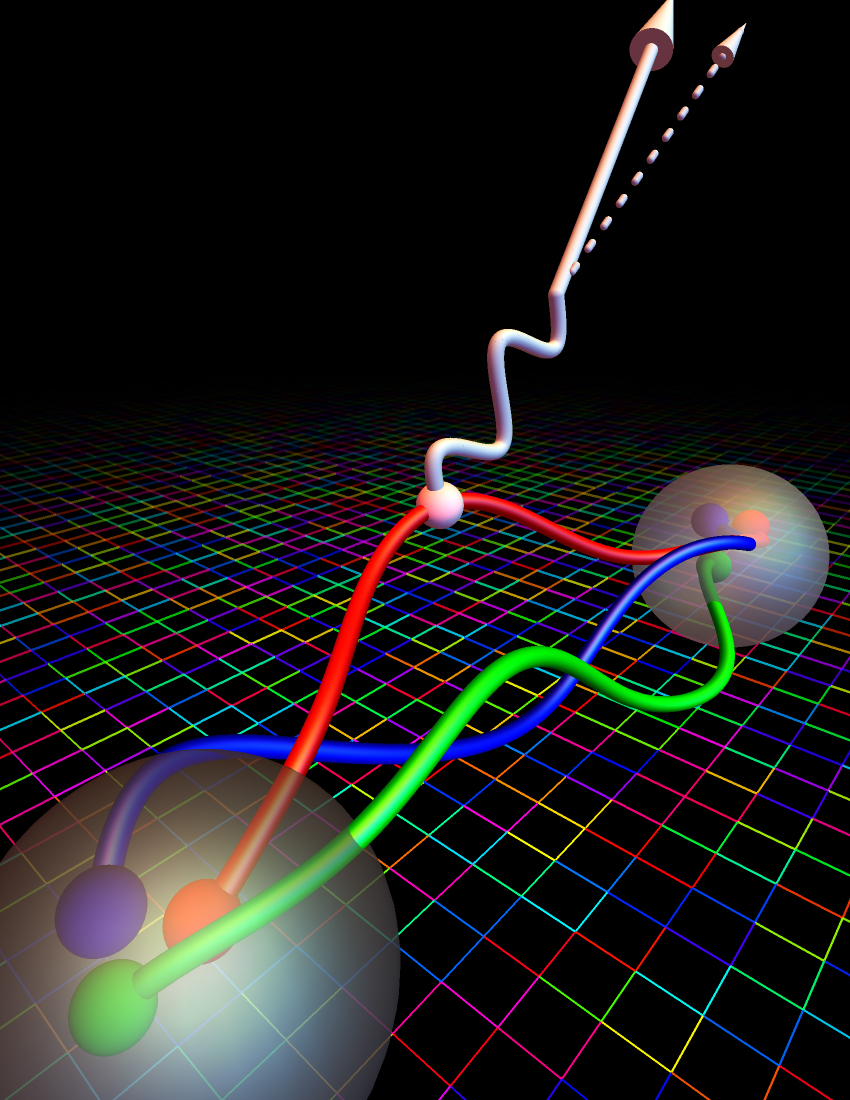
In order to explain the existence of this decay, we would need to both hypothesize a new force (the weak nuclear force) and also a new particle: the W-boson, which must be many times heavier than either the proton or neutron itself to make the numbers work out right. This was bizarre from a theoretical perspective, because as far as we understood particle physics, force-carrying particles (i.e., bosons) had to be massless. In fact, there was a famous theorem known as Goldstone’s Theorem that stated the following:

• if you have a continuous symmetry,
• and that symmetry is spontaneously broken,
• then there will be integer-spin particles (bosons) generated by the breaking of that symmetry,
• and those bosons will be massless and will be generated in numbers that correspond to the number of generators (or degrees of broken symmetry) of that symmetry in particular.

In electroweak theory, where the weak force and electromagnetic force are unified under the symmetry group SU(2)⊗U(1), you would expect three massless (Goldstone) bosons to come out, but that naive prediction violently disagrees with what we know today. There are a total of three bosons associated with the weak interactions — the W+, W-, and Z⁰ bosons — but they’re the opposite of massless: they’re two of the four ultra-heavy particles that are a part of the Standard Model, along with the Higgs boson and top quarks.

The rest masses of the fundamental particles in the Universe determine when and under what conditions they can be created, and also relate to how long they can survive after their creation during the hot Big Bang. The more massive a particle is, the less time it can spontaneously be created in the early Universe, and the shorter its lifetime will be.

The power of the Higgs mechanism

How can you possibly go from the prediction of three massless bosons, in theory, to the physical reality of three not just massive, but ultra-heavy bosons coming into existence when the electroweak symmetry breaks? Although we call it “the Higgs mechanism” today, there were actually three separate teams that all stumbled upon the same basic idea for it way back in 1964: Robert Brout and François Englert, Peter Higgs on his own, and by Gerald Guralnik, Carl Richard Hagen, and Tom Kibble. (Philip Anderson is also sometimes credited for his 1962 paper on a very similar mechanism with applications crossing over from superconductivity into particle physics, but his results were medium-dependent, and couldn’t explain a fundamental, vacuum-only version of the mechanism.)

In the Standard Model, the Higgs field is an SU(2) doublet, which means there are a total of four degrees of freedom. When the Universe cools through the electroweak phase transition, three of those four generators (or “directions” of the field’s group) are spontaneously broken, which would normally give rise to Goldstone bosons. However, because those Goldstone bosons have the same quantum numbers as three of the four electroweak gauge bosons — the ones that will become the W+, W-, and Z⁰ bosons — they mix together, giving them tremendous mass. The components of the electroweak field that do not mix with Goldstone bosons form the massless photon, while the remaining degree of freedom from the Higgs symmetry breaking becomes a new scalar particle: the massive Higgs boson, predicted first by Higgs himself in 1966.

When the electroweak symmetry is broken, the W+ gets its mass by eating the positively charged Higgs, the W- by eating the negatively charged Higgs, and the Z0 by eating the neutral Higgs. The other neutral Higgs becomes the Higgs boson, detected and discovered earlier this decade at the LHC. The photon, the other combination of the W3 and the B boson, remains massless.

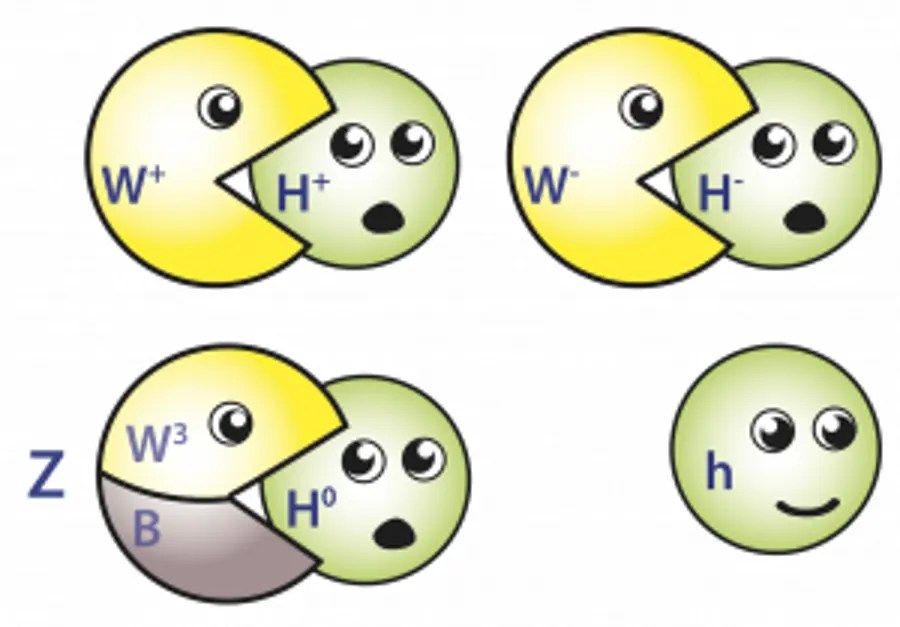
Putting the Higgs mechanism and electroweak theory together in 1967 led to the formulation of the modern Standard Model, and then figuring out QCD as the theory of the strong interactions (in the early 1970s) completed our modern picture that represents our knowledge of the particles and interactions existing throughout the Universe today. There were many who were skeptical, both initially as well as over long periods of time, of the novel mechanism proposed by Higgs and his contemporaries, and it wasn’t until the bona fide discovery of the Higgs boson at CERN in the early 2010s that these doubts were put to rest.

As Gerald Guralnik put it, “We knew that we had indeed done something that was very different and very exciting, but we still didn’t expect it to have something to do with physical reality.”

But indeed, it not only has a lot to do with physical reality, but teaches us that we have a field that permeates all of space, the Higgs field, and that field is responsible for the non-zero rest masses of the known particles, like all species of quarks as well as the electron and its heavier cousins. The big question that now remains is this: is the Higgs boson that we see truly the Standard Model Higgs and the Standard Model Higgs alone, or are there other particles out there — perhaps other Higgs’s, perhaps more exotic particles — that have the same quantum numbers as the Higgs boson and that mix together with it?

When a symmetry is restored (yellow ball at the top), everything is symmetric, and there is no preferred state. When the symmetry is broken at lower energies (blue ball, bottom), the same freedom, of all directions being the same, is no longer present. In the case of the electroweak (or Higgs) symmetry, when it breaks, there’s a spontaneous process that occurs, giving mass to the particles in the Universe.

Breaking the symmetry of the Higgs field

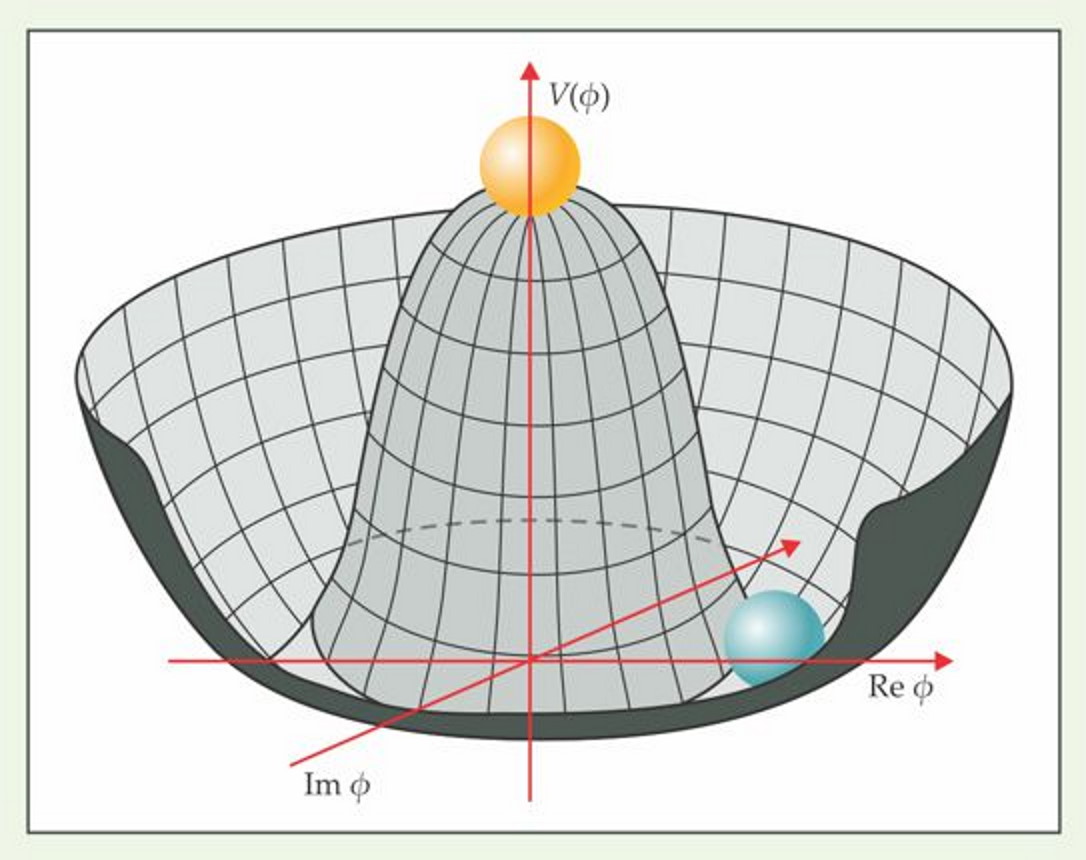
Whenever you have a symmetry that breaks, you can envision it the same way you envision a ball rolling down from the top of a hill or plateau — an unstable point — toward the minimum of the valley down at the bottom of a hill. Although it might not necessarily occur to you, there are two possible ways, in general, for this symmetry-breaking process to proceed.

• The hill or plateau can be smooth and continuous and without any false minima in it (or places where the ball can get “stuck”) as the ball rolls down.
• Or the hill can have at least one additional place along its path where the rolling ball can get “trapped” other than the valley at the very bottom of the hill: with at least one “false minimum” along the way, not just the “true minimum” at the bottom.

In both cases, a symmetry can spontaneously break. In both cases, Goldstone bosons get produced; in both cases as applied to the Higgs mechanism and the electroweak symmetry, you’d get big masses for the W-and-Z bosons as well as the Higgs boson, along with a massless photon.

In the first case, where the hill is smooth all the way down with no false minima in it, the symmetry breaking must proceed smoothly as well: all at once, everywhere, as the Universe cools down from the hot Big Bang. There are no opportunities to get caught in a “false minimum” state; instead, you transition smoothly down to the true vacuum (or ground) state: an example of a second-order phase transition.

In many physical instances, you can find yourself trapped in a local, false minimum, unable to reach the lowest-energy state, which is known as the true minimum. Whether you receive a kick to hurdle the barrier, which can occur classically, or whether you take the purely quantum mechanical path of quantum tunneling, going from one state to another is always possible so long as no fundamental conservation laws are violated. This is an example of a first-order phase transition, rather than a smooth (second-order) transition without any false minima.

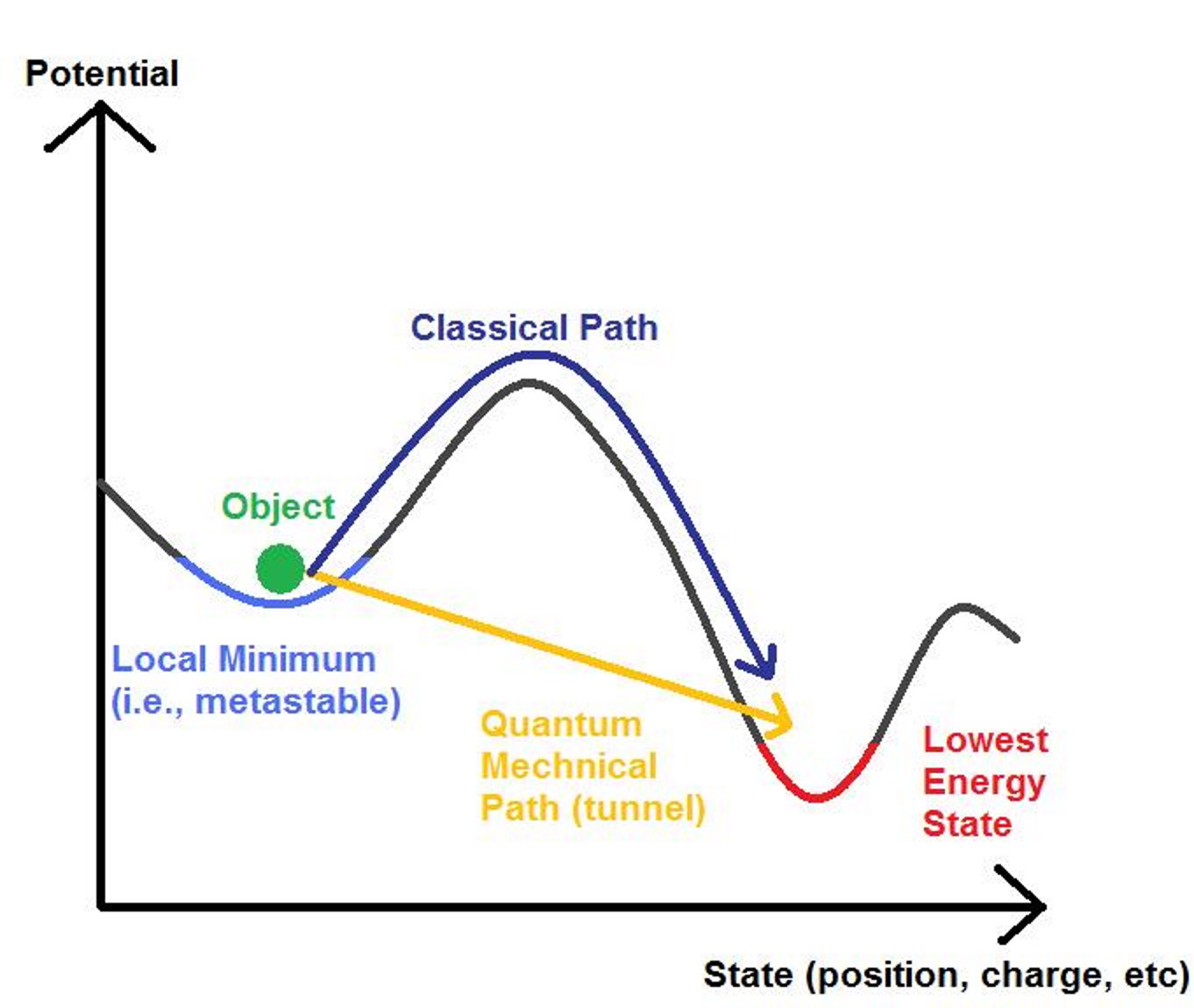
But if there is another particle, set of particles, or new sector of physics to interact and/or mix with the Higgs boson or Higgs field, considered in many extensions of the Standard Model, the broken symmetry of the Higgs field might not be a smooth, false-minimum-free transition, but could be one where the shape of the potential changes to become first-order: with a false minimum, where the only way to reach the true vacuum state is to quantum tunnel out of this false minimum and into the true minimum.

Now, you might think to ask just why the shape of the potential that take place during this phase of symmetry breaking is so important to the Universe, and the answer goes all the way back to one of the biggest existential questions about our Universe: why it’s made overwhelmingly of matter, and not with a corresponding equal-and-opposite amount of antimatter?

Because there are three conditions necessary to create a matter-antimatter symmetry out of nothing, known as the Sakharov conditions. They are:

1. an out-of-equilibrium set of conditions,
2. a sufficient amount of C-violating (charge conjugation symmetry-violating) and CP-violating (charge conjugation + parity symmetry-violating, combined) interactions,
3. and baryon-number violating interactions,

all occurring together. Wherever these three conditions coincide, it’s possible, and sometimes mandatory, that a matter-antimatter asymmetry can be generated even from perfectly symmetric initial conditions.

When the electroweak symmetry (the symmetry that corresponds to the Higgs field) breaks, the combination of CP-violation and baryon number violation can create a matter/antimatter asymmetry where there was none before, owing to the effect of sphaleron interactions working on, for example, a neutrino excess. This can only occur, however, if the electroweak phase transition is first-order, rather than the second-order transition predicted by the Standard Model alone.

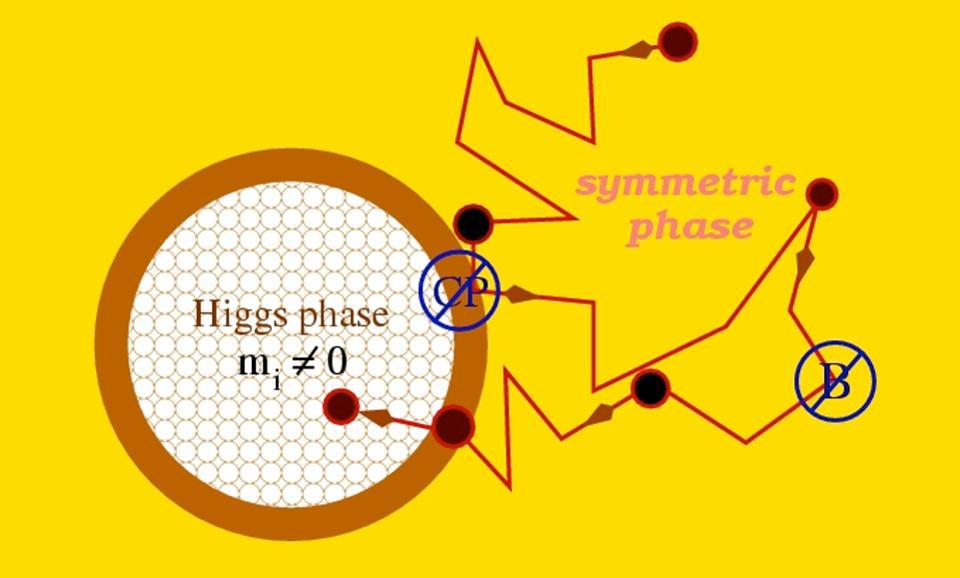
Electroweak baryogenesis

As it stands today, there are only four realistic scenarios that exist within our Universe, that don’t already disagree with established physics, that can create a matter-antimatter asymmetry from an initially symmetric state. One of them, GUT baryogenesis, should only occur at energies that are billions of times greater than what current collider experiments (like the LHC) can achieve, and is disfavored by the lack of observed proton decay as well as modern theories of inflation. Another, leptogenesis, occurs at similarly high, inaccessible energies. A third, via the Affleck-Dine mechanism, is entirely reliant on supersymmetry existing and existing at collider-accessible scales: something that flies in the face of experiment.

But the fourth is known as electroweak baryogenesis, and is something that we can search for with current collider technology. If all we have is the basic Standard Model, which gives us the C-violation and CP-violation observed in weak decays and a second-order phase transition for the Higgs mechanism, we get only a negligible matter-antimatter mismatch out: one that’s too small by a factor of about 10 billion to agree with observation. The only way we can get any baryogenesis at all in this scenario is through a process known as the sphaleron process: where baryon number (B) and lepton number (L) are each individually violated, but where the combination of B – L (baryon number minus lepton number) is conserved.

In a 2024 study by the CMS collaboration, a search for exotic particles, bottom-type vector-like quarks, is conducted. These particles are expected to exist in many scenarios that involve additional Higgs boson-like particles that would mix with the known Higgs. No evidence is seen for these particles, constraining the possible existence of these scenarios and a first-order electroweak phase transition.

However, we know the Standard Model isn’t all there is to reality. If it were, there would be no physical explanation for:

• dark matter,
• dark energy,
• cosmic inflation,
• or the matter-antimatter asymmetry,

and we have many different lines of evidence pointing to the reality of existence of all four of these. If there is, for example, an electroweak-scale singlet scalar field, such as one that arises from a composite Higgs model or a multiple Higgs-doublet model, then the mechanism that leads to the breaking of the Higgs symmetry might be first-order, not second-order.

In this scenario, the Higgs field can take on different values over different regions of space as the symmetry breaks, creating severe out-of-equilibrium conditions. Depending on what types of C-violation and CP-violation exist, there can be enough baryon number-violating interactions to explain the entirety of the matter-antimatter asymmetry, and there could even be signatures that current colliders, like the LHC, are sensitive to.

It should be noted that higher-energy-scale particles that mix with the Higgs, including theoretical scenarios like the dilaton or even inflationary ones that include a scalar inflation, might also mix with the Higgs, creating a first-order phase transition along with other signals that are potentially observable elsewhere, such as at collider or even in gravitational wave detectors.

If there’s a strongly first-order electroweak phase transition, then in addition to the gravitational wave background produced by inflation (black line), there should be a new spectrum of gravitational waves (red peak) produced that upcoming gravitational wave observatories, such as the upcoming LISA, will be sensitive to.

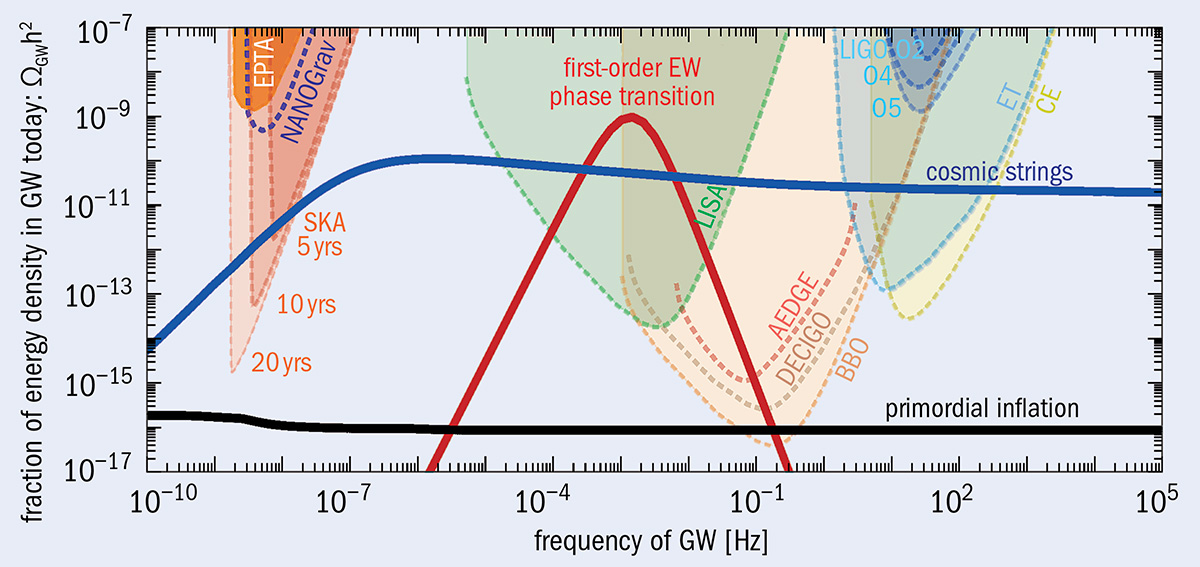
How will we find out?

It isn’t just through direct evidence, like the creation of fundamentally new particles, that new physics can be revealed. We can search for the types of particle signatures that should exist if there are extra particles that couple to and mix with the Higgs. We can look for related signals that arise in gravitational wave detectors. We can create enormous numbers of Higgs bosons and look for any signature of a departure — at the 0.1% level, the 0.01% level, the 0.001% level, etc. — from the pure predictions of the Standard Model alone. And we can even create a relativistic quark-gluon plasma at sufficiently high energies to try to directly create reactions that, at the end of the day, will have violated the baryon number directly.

When most of us think of experimental particle physics, these aren’t considerations that are normally at the top of our mind. We think about the possibility of finding new particles directly and of breaking the Standard Model: by discovering things that it can’t account for. But among the things that the Standard Model alone cannot account for, including

• dark matter,
• dark energy,
• cosmic inflation,
• and the matter-antimatter asymmetry,

we have to consider the value of probing potential links between phenomena accessible at colliders and these tremendous existential questions. Despite all we know about the Higgs and physics at the electroweak scale, we don’t yet know whether the electroweak phase transition is first-order or second-order. With one of the greatest open questions in physics possibly within reach if nature is kind, we owe it to humanity and our own spirit of curiosity to investigate this accessible avenue as thoroughly as possible.