How do Black Holes evaporate?

They’re the densest objects in the Universe, but even they won’t live forever. Here’s why not.

“It’s like, how much more black could this be? And the answer is none. None more black.” -Nigel Tufnel, This is Spinal Tap

So you’ve heard of black holes: regions of space where matter-and-energy is concentrated so densely that nothing, not even light can escape from it.

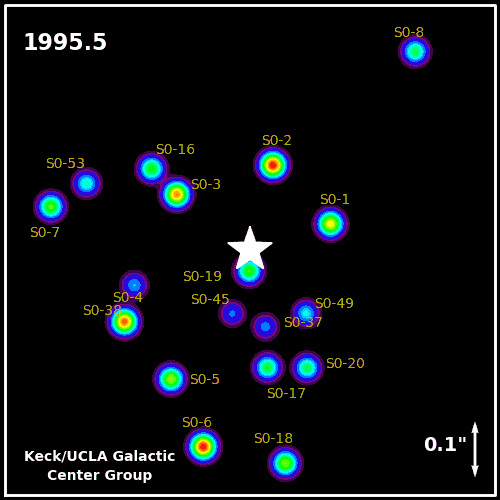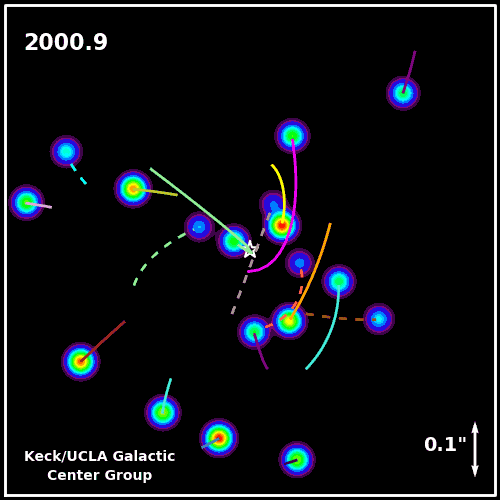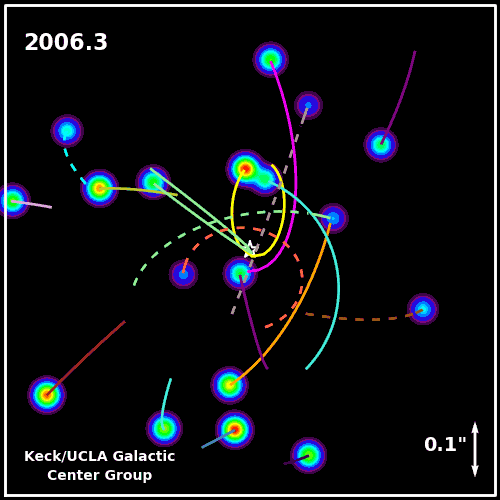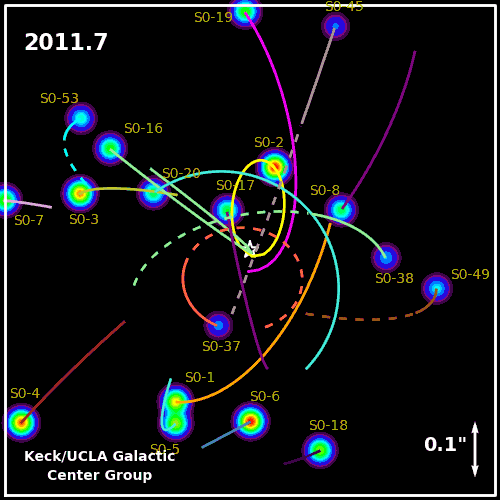
These objects most certainly exist, and are known to range in size from just a few times the mass of our Sun (like Cygnus X-1, illustrated above) to the supermassive ones at the centers of galaxies. Our galaxy has one that’s about four million times the mass of the Sun (below), but the largest ones can be many billions (or even tens of billions) of times as massive as our Sun.

The smaller ones are formed when very massive stars — stars around 12-15 times the mass of our Sun (or more) — run out of nuclear fuel in their core. When the fuel runs out, the core collapses under its own gravity. For smaller stars, the quantum properties of the atoms can hold it up against gravity, for larger (maybe 7-12 times the mass of our Sun) stars, the core will fuse into a huge collection of neutrons, which can themselves stand against gravity, creating a neutron star. But above a certain limit, not even the neutrons themselves can resist the force of gravity; the result will be a black hole.

And, of course, you can make even bigger ones by mergers and other processes; the Universe is no doubt rich with them. But if not even light can escape from a black hole, how is it that they’ll evaporate?

You might have heard of terms like the Heisenberg Uncertainty Principle and Hawking radiation, and at first pass, this might appear to explain it. Let’s take a look at the first one.

One of the fundamental “weird” things about quantum mechanics is that it tells you that you cannot measure the energy of a system to an arbitrary accuracy in a finite amount of time: there’s an inherent energy-time uncertainty. This means a lot of things: particles that live a very short time (like the Higgs boson or the top quark) have an inherent uncertainty in their mass, that the measurement of a systems mass or energy cannot be achieved instantaneously, and — perhaps most importantly — that even completely empty space itself can have a non-zero energy to it.

Thanks to quantum mechanics, we even have a way to visualize this.

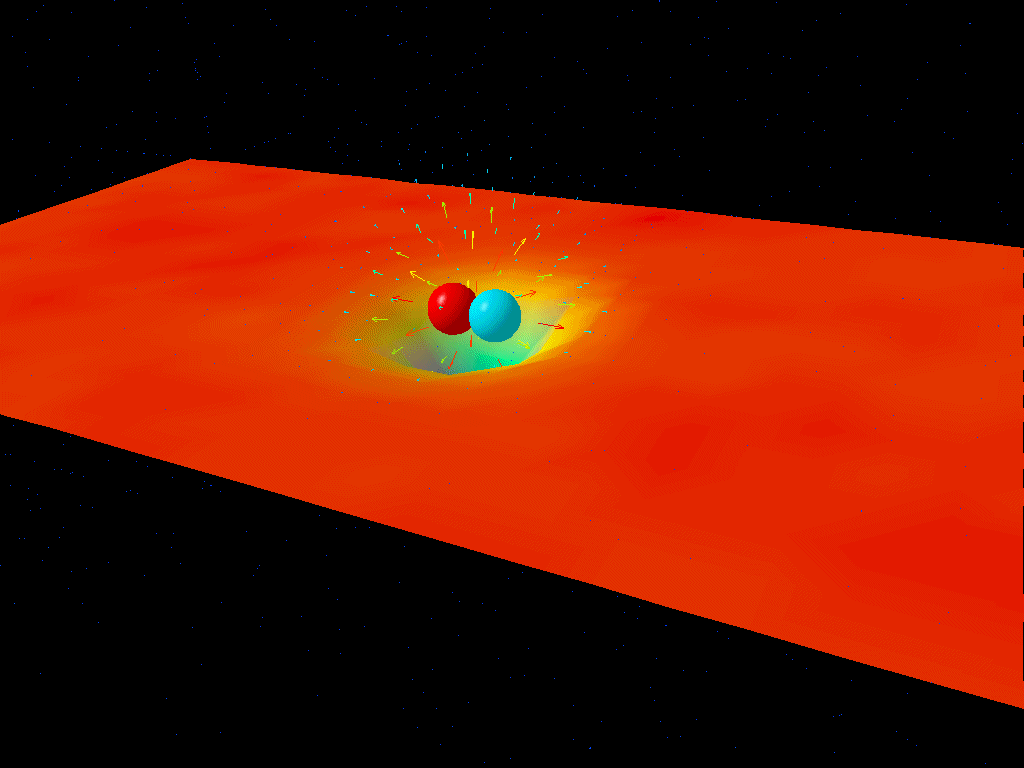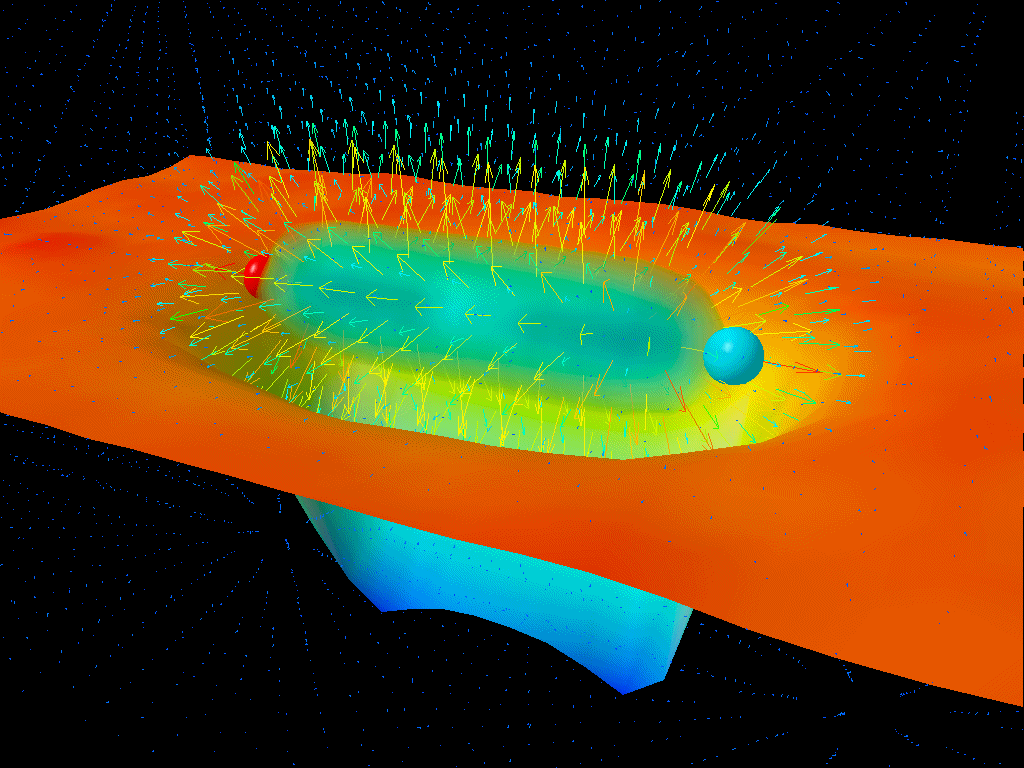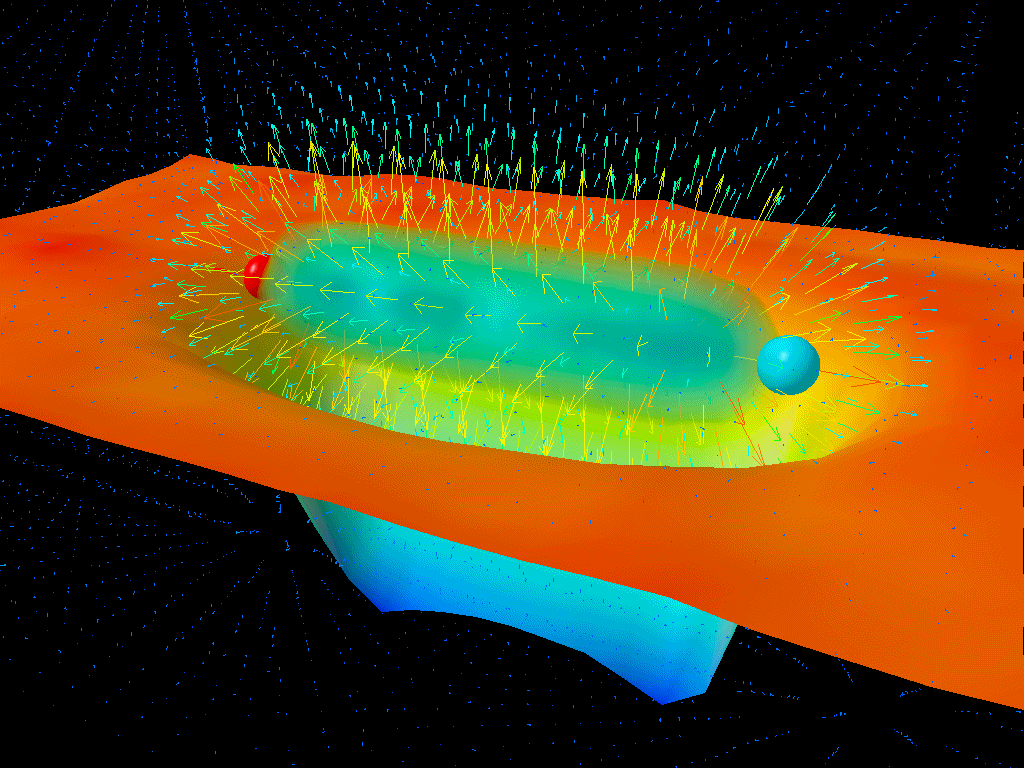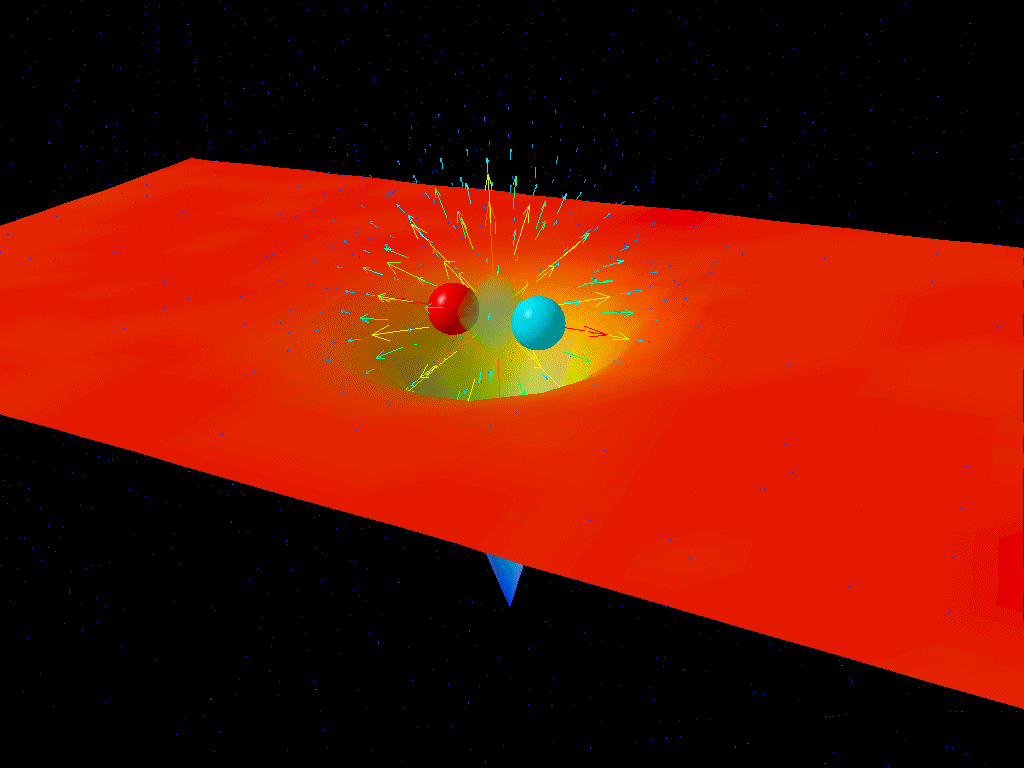
Pairs of quantum particles-and-antiparticles can pop in-and-out of existence for very brief periods of time. So long as they obey the Heisenberg Uncertainty Principle, this is not only possible, it’s inevitable! And with this picture in mind, you may think you can come up with a way to make your black holes decay.

You see, black holes — regardless of size — have an event horizon, or a location beyond which nothing can get out. Inside the event horizon, everything is trapped: any matter in there stays in there, any particle-antiparticle pairs remain inside, any light that enters cannot escape. Outside that event horizon, however, things can either remain outside or fall in. And if you’ve got particle-antiparticle pairs forming on the outside, you can imagine that most of the time, they’ll annihilate outside, but once in a rare while, one of the pairs can fall in, while the other one remains outside!

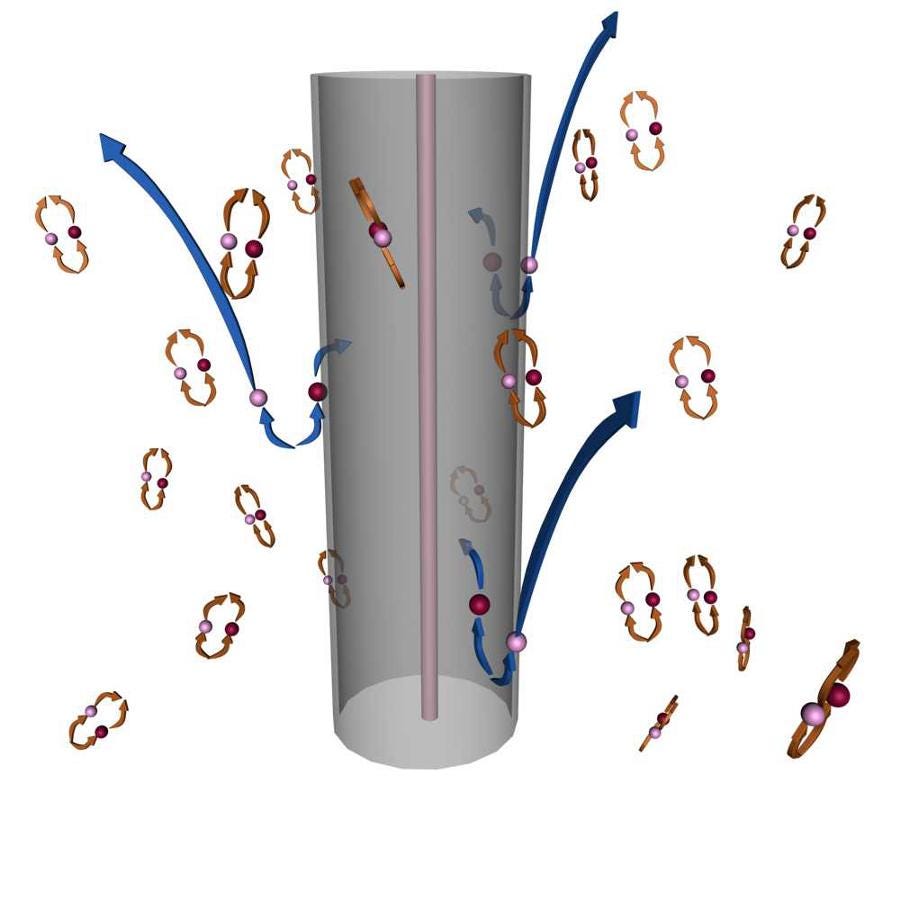
This is a beautiful, tempting picture, but it’s also not quite complete. There are a few problems with it that I myself have glossed over in the past, and it’s time to address them now.

For one, particles “cost energy,” so to speak, and by the conservation of energy, you can’t just make them for free out of nothing. Even quantum uncertainty only allows you to “cheat” the Universe out of energy for that tiny amount of time; eventually you have to give it back!

For another, the temperature of the radiation due to this mechanism can be calculated, and the only thing it’s dependent on is the mass of the black hole we’re right outside of.

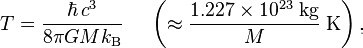
While it takes literally billions of degrees of temperature to create the lightest particle/antiparticle pairs (not counting neutrinos, which would come in at a few degrees), a black hole the mass of our Sun would have a temperature of less than one microKelvin, and the temperature only goes down for more massive ones. In other words, the energy simply isn’t there to make even one of these particles.

So what’s the way out? What really happens?

You have to remember that these are not real particles but rather virtual particles that are being created. The “quantum mechanical” picture I showed you earlier is a non-relativistic visualization of the underlying relativistic quantum field theory that better describes our Universe. Rather than “real particle-antiparticle pairs,” these are better visualized as virtual particles that never physically exist (i.e., with mass and collisions), but that can live for limited amounts of time so long as the final end state is consistent with all the known conservation laws.

With that in mind, what’s happening just outside the event horizon of a black hole?

Yes, you make these virtual particle-antiparticle pairs all the time; in some cases, the particle falls in and the antiparticle remains on the outside, and in some cases the antiparticle falls in and the particle remains on the outside. But it’s when you have two of these virtual particle pairs doing this in such a way that it matches the right conditions that you can get real radiation coming out of your black hole!

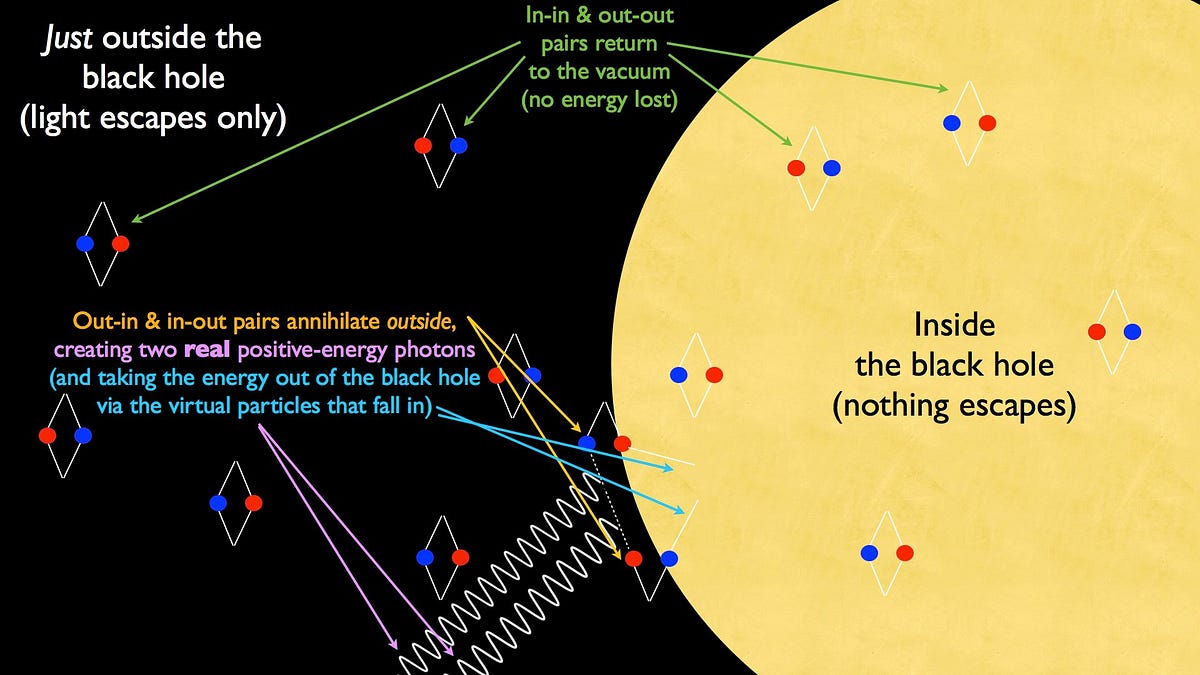
Imagine you have two particle-antiparticle pairs just outside the event horizon: for pair one, the antiparticle falls in and the particle escapes, while for pair two, the particle falls in and the antiparticle escapes. The escaping particle from pair one and antiparticle from pair two interact, producing two photons (which is what you need to conserve both energy and momentum), which can escape as Hawking radiation with real, positive energy.

But that energy isn’t free! Where did it come from? It must be subtracted from the mass of the black hole, something that can happen thanks to the infalling virtual particles from the original “in” part of the “out-in” pair and the “in-out” pair, respectively. So in the end, we have escaping radiation and a lower mass for the black hole!

Although the only way to get the exact answer is to do the quantum field theory calculations in strongly curved space, this picture I’ve outlined for you is very, very close to what actually happens. The subtle difference is that the radiation emitted is blackbody and continuous, something you wouldn’t know from the picture I painted, above. What’s also amazing is that the rate of energy loss (encoded in the temperature of the hole) is faster around lower mass black holes, since the curvature of space actually is more intense around event horizons for small black holes!

It would take a whopping ~10^67 years for a black hole the mass of the Sun to evaporate, and around ~10^100 years for the largest black holes in the Universe. That may be far longer than the age of the Universe, but it’s still not forever. Although black holes may live longer than any other object known in the Universe, even they have their limits, and now you know how come!