If the Hubble tension is real, what’s the solution?

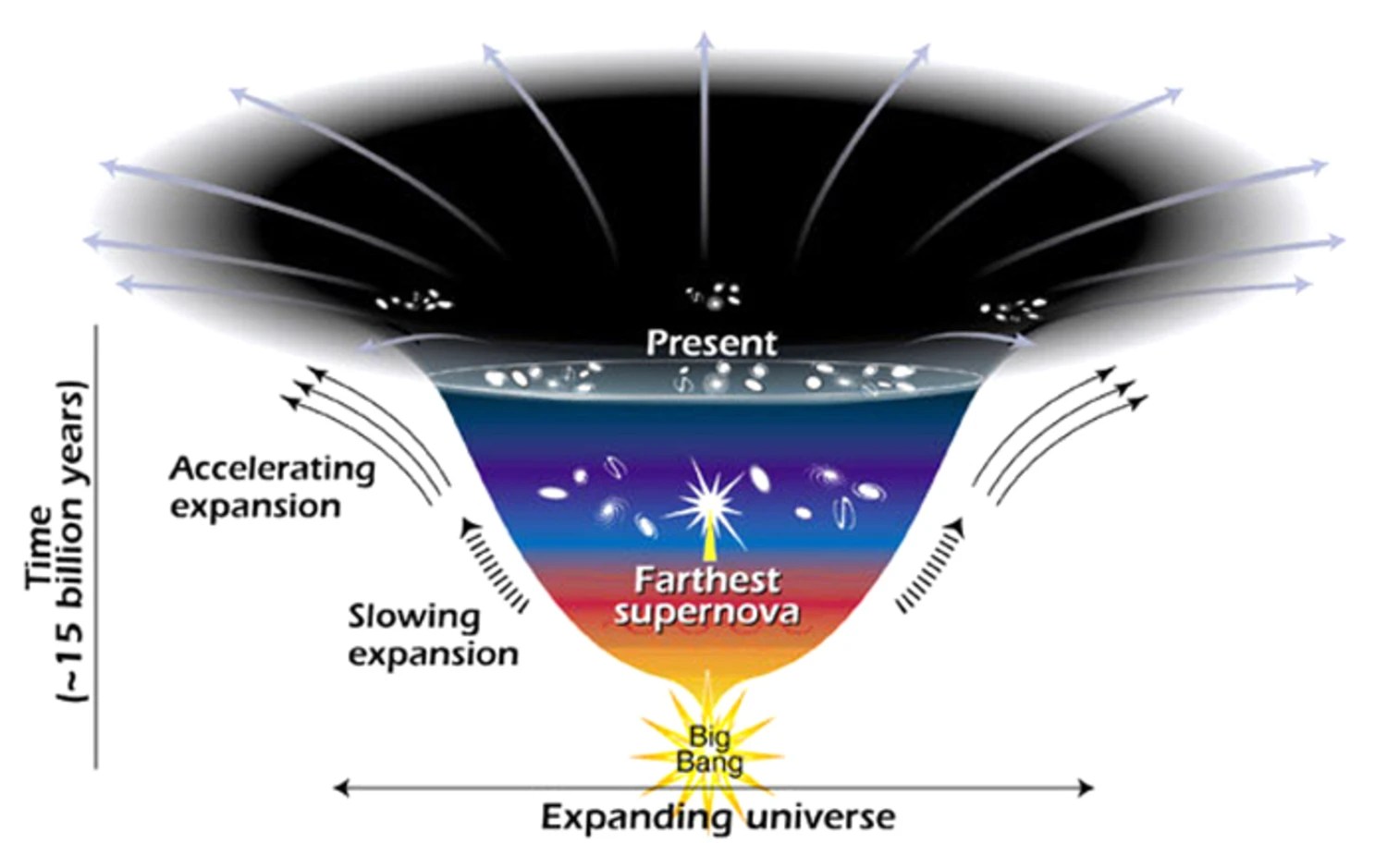
No matter how one approaches a problem, if everyone’s method is sound, they should all always arrive at the same correct solution. This applies not only to the puzzles we create for our fellow humans here on Earth, but also to the deepest puzzles that nature has to offer. One of the greatest challenges we can dare to pursue is to uncover how the Universe has expanded throughout its history: from the Big Bang all the way up to today. You can imagine two wildly different methods that should both be valid:

1. Start at the beginning, evolve the Universe forward in time according to the laws of physics, and then measure those earliest relic signals and their imprints on the Universe to determine how it has expanded over its history.
2. Alternatively, you can imagine starting at the here-and-now, looking out at the distant objects for as far as we can see them receding from us, and then to draw conclusions as to how the Universe has expanded from that data.

Both of these methods rely on the same laws of physics, the same underlying theory of gravity, the same cosmic ingredients, and even the same equations as one another. And yet, when we actually perform our observations and make those critical measurements, we get two completely different answers that don’t agree with one another. This problem, that the first method yields 67 km/s/Mpc and the second yields 73-to-74 km/s/Mpc, with only a ~1% uncertainty to each method, is known as the Hubble tension, and is arguably the most pressing problem in cosmology today.

Some still hold out hope that the true answer lies somewhere between these two extremes, but the errors are small and both groups are confident in their conclusions. So if they’re both correct, what does that mean for the Universe?

A plot of the apparent expansion rate (y-axis) vs. distance (x-axis) is consistent with a Universe that expanded faster in the past, but where distant galaxies are accelerating in their recession today. This is a modern version of, extending thousands of times farther than, Hubble’s original work. Note the fact that the points do not form a straight line, indicating the expansion rate’s change over time. The fact that the Universe follows the curve it does is indicative of the presence, and late-time dominance, of dark energy.

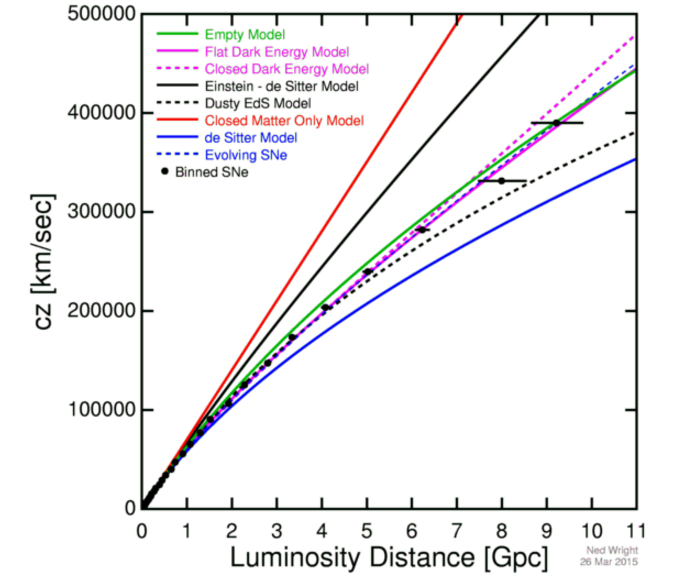
The basics of expansion

One of the great theoretical developments of modern astrophysics and cosmology comes straight out of general relativity and just one simple realization: that the Universe, on the largest cosmic scales, is both:

1. uniform, or the same at all locations
2. isotropic, or the same in all directions

As soon as you make those two assumptions, the Einstein field equations — the equations that govern how the curvature and expansion of spacetime and the matter and energy contents of the Universe are related to each other — reduce to very simple, straightforward rules.

Those rules teach us that the Universe cannot be static, but rather must be either expanding or contracting, and that measuring the Universe itself is the only way to determine which scenario is true. Furthermore, measuring how the expansion rate has changed over time teaches you what’s present in our Universe and in what relative amounts. Similarly, if you know how the Universe expands at any one point in its history, and also what all the different forms of matter and energy are present in the Universe, you can determine how it has expanded and how it will expand at any point in the past or future. It’s an incredibly powerful piece of theoretical weaponry.

The construction of the cosmic distance ladder involves going from our Solar System to the stars to nearby galaxies to distant ones. Each “step” carries along its own uncertainties, especially the steps where the different “rungs” of the ladder connect. However, recent improvements in the distance ladder have demonstrated how robust its results are.

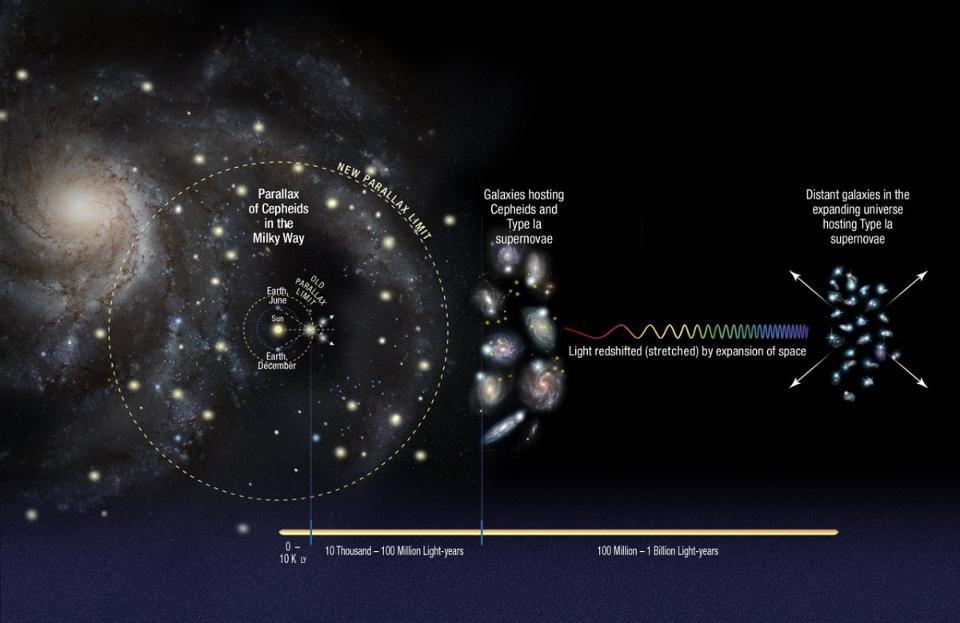
The distance ladder method

One strategy is as straightforward as it gets.

First, you measure the distances to the astronomical objects that you can take those measurements of directly.

Then, you try to find correlations between intrinsic properties of those objects that you can easily measure, like how long a variable star takes to brighten to its maximum, fade to a minimum, and then re-brighten to its maximum again, as well as something that’s more difficult to measure, like how intrinsically bright that object is.

Next, you find those same types of objects farther away, like in galaxies other than the Milky Way, and you use the measurements you can make — along with your knowledge of how observed brightness and distance are related to one another — to determine the distance to those galaxies.

Afterward, you measure extremely bright events or properties of those galaxies, like how their surface brightnesses fluctuate, how the stars within them revolve around the galactic center, or how certain bright events, like supernovae, occur within them.

And finally, you look for those same signatures in faraway galaxies, again hoping to use the nearby objects to “anchor” your more distant observations, providing you with a way to measure the distances to very faraway objects while also being able to measure how much the Universe has cumulatively expanded over the time from when the light was emitted to when it arrives at our eyes.

Many different classes of objects and measurements are used to determine the relationship between distance to an object and its apparent speed of recession that we infer from its light’s relative redshift with respect to us. As you can see, from the very nearby Universe (lower left) to distant locations more than 10 billion light-years away (upper right), this very consistent redshift-distance relation continues to hold.

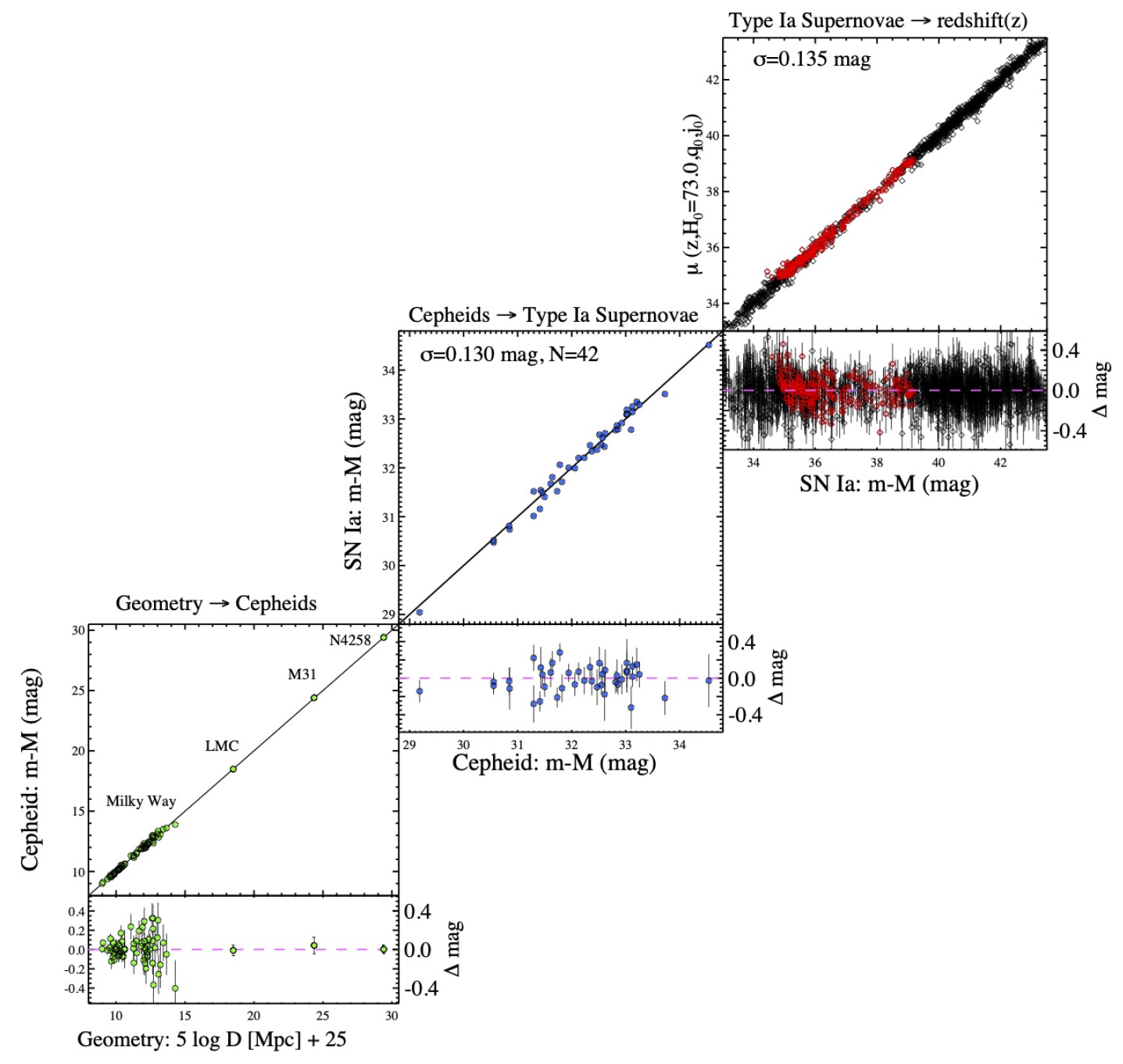
We call this method the cosmic distance ladder, since each “rung” on the ladder is straightforward but moving to the next one farther out relies on the sturdiness of the rung beneath it. For a long time, an enormous number of rungs were required to go out to the farthest distances in the Universe, and it was exceedingly difficult to reach distances of a billion light-years or more.

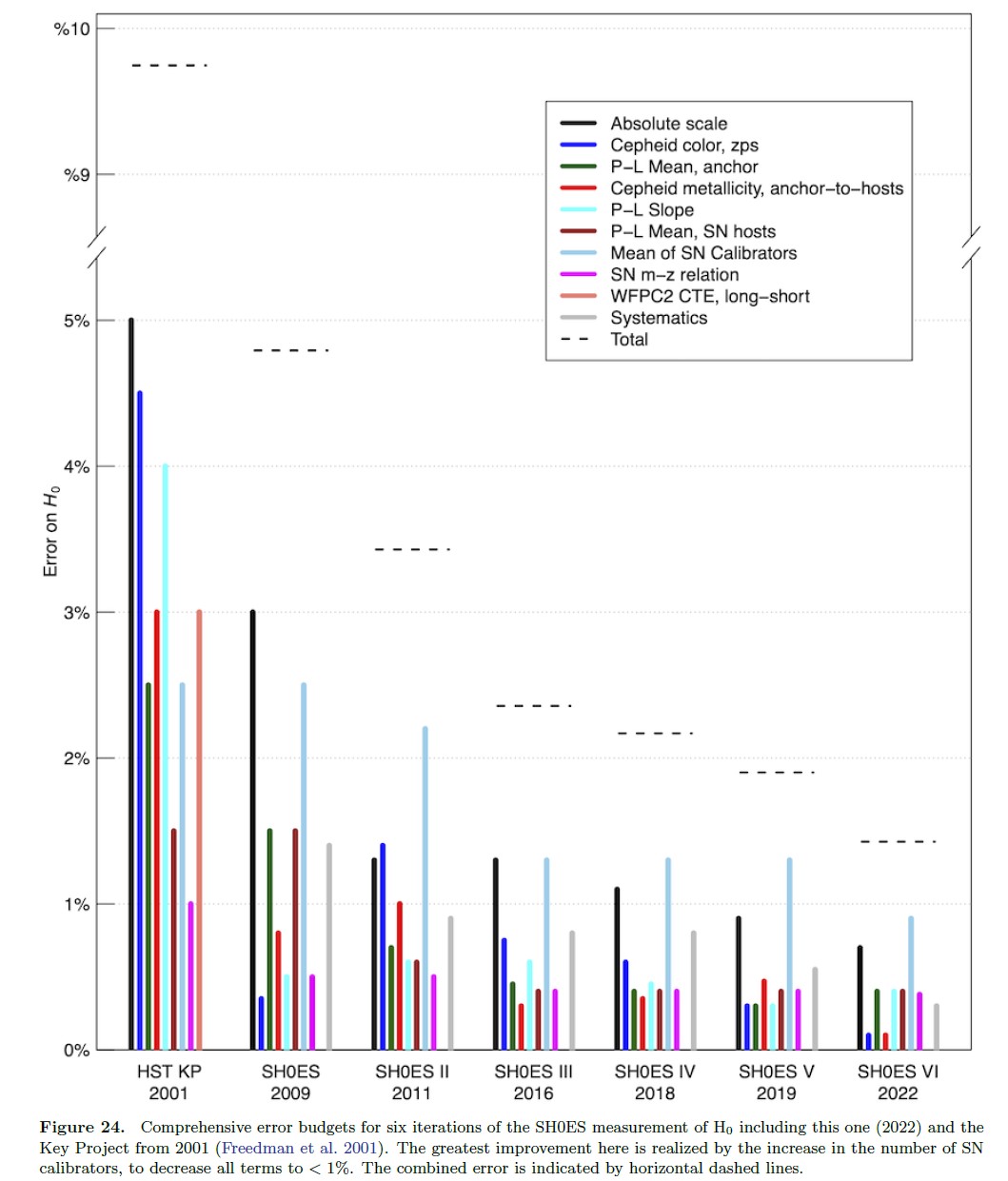
With recent advances in not only telescope technology and observational techniques, but also in understanding the uncertainties surrounding the individual measurements, we’ve been able to completely revolutionize distance ladder science.

About 40 years ago, there were perhaps seven or eight rungs on the distance ladder, they brought you out to distances of under a billion light-years, and the uncertainty in the rate of expansion of the Universe was about a factor of 2: between 50 and 100 km/s/Mpc.

Two decades ago, the results of the Hubble Space Telescope Key Project were released and the number of necessary rungs was brought down to about five, distances brought you out to a few billion light-years, and the uncertainty in the expansion rate reduced to a much smaller value: between 65 and 79 km/s/Mpc.

Back in 2001, there were many different sources of error that could have biased the best distance ladder measurements of the Hubble constant, and the expansion of the Universe, to substantially higher or lower values. Thanks to the painstaking and careful work of many, that is no longer possible, as errors have been greatly reduced. New JWST work, not shown here, has reduced Cepheid-related and period-luminosity errors even further than is shown here.

Today, however, there are only three rungs needed on the distance ladder, as we can go directly from measuring the parallax of variable stars (such as Cepheids), which tells us the distance to them, to measuring those same classes of stars in nearby galaxies (where those galaxies have contained at least one type Ia supernova), to measuring type Ia supernovae out to the farthest reaches of the distant Universe where we can see them: up to tens of billions of light-years away.

Through a Herculean set of efforts from many observational astronomers, all the uncertainties that had long plagued these differing sets of observations have been reduced below the ~1% level. All told, the expansion rate is now robustly determined to be about 73-to-74 km/s/Mpc, with an uncertainty of merely ±1 km/s/Mpc atop that. For the first time in history, the cosmic distance ladder, from the present day looking back more than 10 billion years in cosmic history, has given us the expansion rate of the Universe to a very high precision.

Although we can measure the temperature variations all across the sky, on all angular scales, it’s the peaks and valleys in the temperature fluctuations that teach us about the ratio of normal matter to dark matter, as well as the length/size of the acoustic scale, where normal matter (but not dark matter) gets “bounced” outward from interactions with radiation. This radiation includes photons, which have a substantial cross-section with particles in the ionized plasma of the early Universe, and neutrinos, which do not.

The early relic method

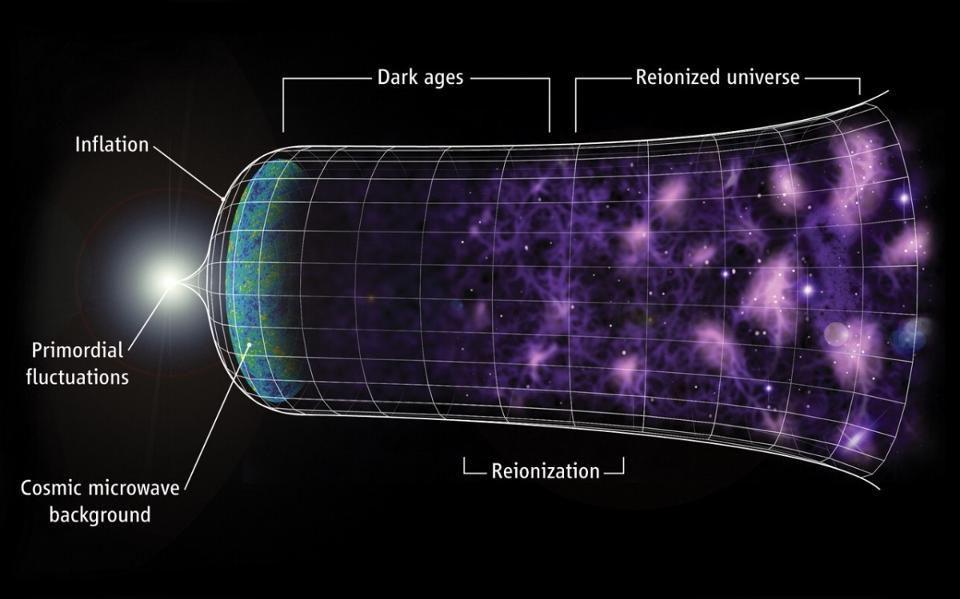
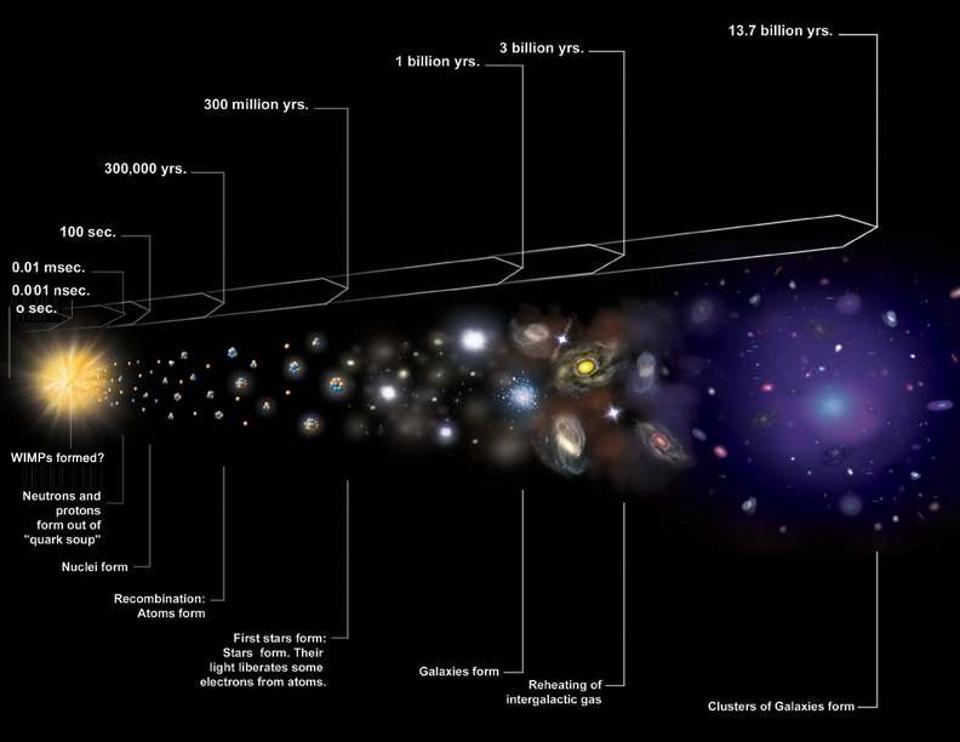
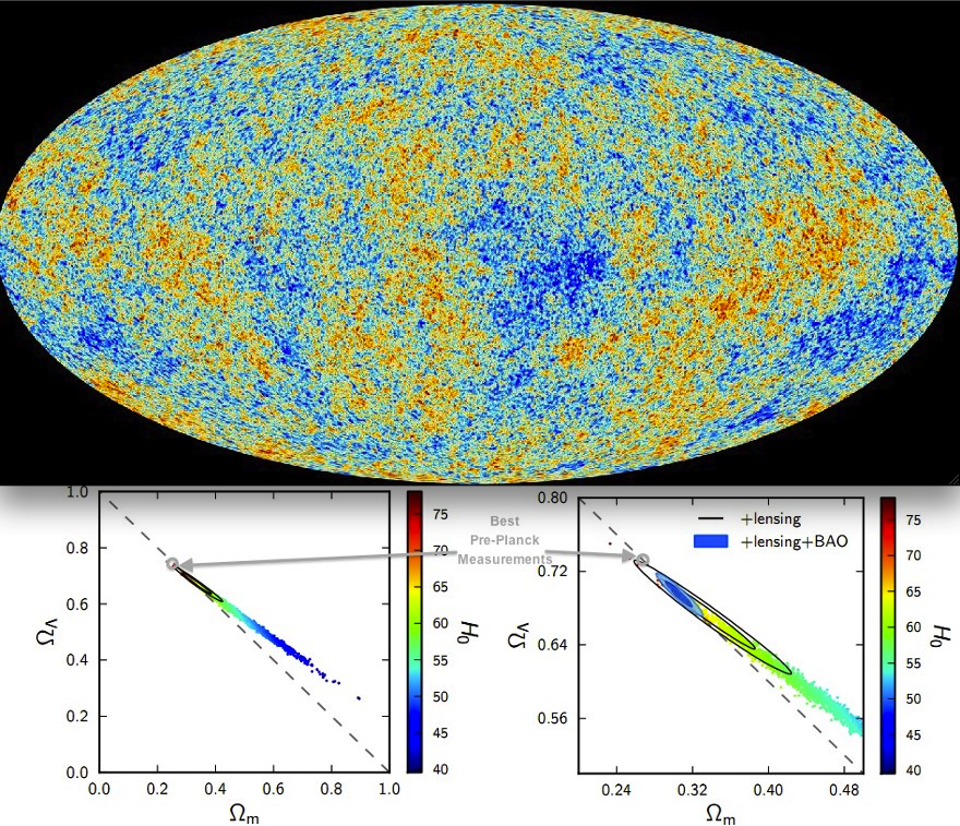
Meanwhile, there’s a completely different method we can use to independently “solve” the exact same puzzle: the early relic method. When the hot Big Bang begins, the Universe is almost, but not quite perfectly, uniform. While the temperatures and densities are initially the same everywhere — in all locations and in all directions, to 99.997% precision — there are those tiny ~0.003% imperfections in both.

Theoretically, they were generated by cosmic inflation, which predicts their spectrum very accurately. Dynamically, the regions of slightly higher-than-average density will preferentially attract more and more matter into them, leading to the gravitational growth of structure and, eventually, the entire cosmic web. However, the presence of two types of matter — normal and dark matter — as well as radiation, which collides with normal matter but not with dark matter, causes what we call “acoustic peaks,” meaning that the matter tries to collapse, but rebounds, creating a series of peaks and valleys in the densities we observe on various scales.

An illustration of clustering patterns due to Baryon Acoustic Oscillations, where the likelihood of finding a galaxy at a certain distance from any other galaxy is governed by the relationship between dark matter and normal matter, as well as the effects of normal matter as it interacts with radiation. As the Universe expands, this characteristic distance expands as well, allowing us to measure the Hubble constant, the dark matter density, and even the scalar spectral index. The results agree with the CMB data, and a Universe made up of ~25% dark matter, as opposed to 5% normal matter, with an expansion rate of around 67 km/s/Mpc.

These peaks and valleys show up in two places at very early times.

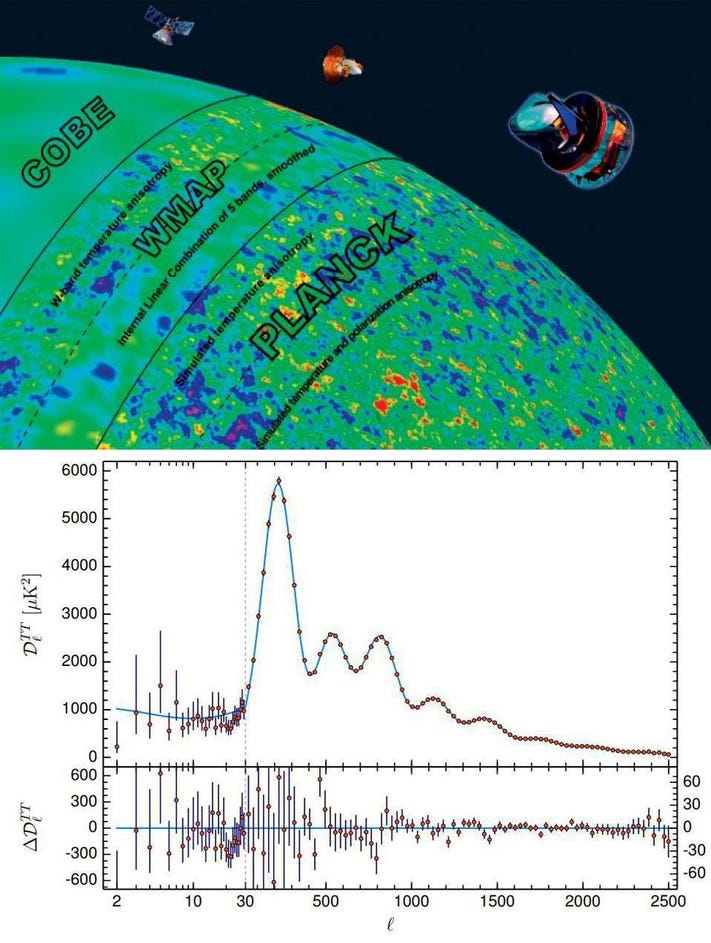
They appear in the leftover glow from the Big Bang: the cosmic microwave background. When we look at the temperature fluctuations — or, the departures from the average (2.725 K) temperature in the radiation leftover from the Big Bang — we find that they’re roughly ~0.003% of that magnitude on large cosmic scales, rising to a maximum of about ~1 degree on smaller angular scales. They then rise, fall, rise again, etc., for a total of about seven acoustic peaks. The size and scale of these peaks, calculable from when the Universe was only 380,000 years old, then come to us at present dependent solely on how the Universe has expanded from the time that light was emitted, all the way back then, to the present day, 13.8 billion years later.

They show up in the large-scale clustering of galaxies, where that original ~1-degree-scale peak has now expanded to correspond to a distance of around 500 million light-years. Wherever you have a galaxy, you’re somewhat more likely to find another galaxy 500 million light-years away than you are to find one either 400 million or 600 million light-years away: evidence of that very same imprint. By tracing how that distance scale has changed as the Universe has expanded — by using a standard “ruler” instead of a standard “candle” — we can determine how the Universe has expanded over its history.

Standard candles (left) and standard rulers (right) are two different techniques astronomers used to measure the expansion of space at various times/distances in the past. Based on how quantities like luminosity or angular size change with distance, we can infer the expansion history of the Universe. Using the candle method is part of the distance ladder, yielding 73 km/s/Mpc. Using the ruler is part of the early signal method, yielding 67 km/s/Mpc. With new JWST data, the mystery over the Universe’s expansion rate has deepened further.

The issue with this is that, whether you use the cosmic microwave background or the features we see in the large-scale structure of the Universe, you get a consistent answer: 67 km/s/Mpc, with an uncertainty of only ±0.7 km/s/Mpc, or ~1%.

That’s the problem. That’s the puzzle. We have two fundamentally different ways of how the Universe has expanded over its history. Each is entirely self-consistent. All distance ladder methods and all early relic methods give the same answers as one another, and those answers fundamentally disagree between those two methods.

If there truly are no major errors that either sets of teams are making, then something simply doesn’t add up about our understanding of how the Universe has expanded. From 380,000 years after the Big Bang to the present day, 13.8 billion years later, we know:

• how much the Universe has expanded by
• the ingredients of the various types of energy that exist in the Universe
• the rules that govern the Universe, like general relativity

Unless there’s a mistake somewhere that we haven’t identified, it’s extremely difficult to concoct an explanation that reconciles these two classes of measurements without invoking some sort of new, exotic physics.

A series of different groups seeking to measure the expansion rate of the Universe, along with their color-coded results. Note how there’s a large discrepancy between early-time (top two) and late-time (other) results, with the error bars being much larger on each of the late-time options. Although these two classes of measurements give incompatible results, no one knows the resolution to why the Universe appears to expand differently dependent on the method used to measure the expansion.

The heart of the puzzle

If we know what’s in the Universe, in terms of normal matter, dark matter, radiation, neutrinos, and dark energy, then we know how the Universe expanded from the Big Bang until the emission of the cosmic microwave background, and from the emission of the cosmic microwave background until the present day.

That first step, from the Big Bang until the emission of the cosmic microwave background, sets the acoustic scale (the scales of the peaks and valleys), and that’s a scale that we measure directly at a variety of cosmic times. We know how the Universe expanded from 380,000 years of age to the present, and “67 km/s/Mpc” is the only value that gives you the right acoustic scale at those early times.

Meanwhile, that second step, from after the cosmic microwave background was emitted until now, can be measured directly from stars, galaxies, and stellar explosions, and “73 km/s/Mpc” is the only value that gives you the right expansion rate. There are no changes you can make in that regime, including changes to how dark energy behaves (within the already-existing observational constraints), that can account for this discrepancy.

Other, less precise methods average out to about ~70 km/s/Mpc in their estimates for the rate of cosmic expansion, and you can just barely justify consistency with the data across all methods if you force that value to be correct. But with incredible CMB/BAO data to set the acoustic scale and remarkably precise type Ia supernova to measure expansion via the distance ladder, even 70 km/s/Mpc is stretching the limits of both sets of data.

The best map of the CMB and the best constraints on dark energy and the Hubble parameter from it. We arrive at a Universe that’s 68% dark energy, 27% dark matter, and just 5% normal matter from this and other lines of evidence, with a best-fit expansion rate of 67 km/s/Mpc. There is no wiggle-room that allows that value to rise to ~73 and still be consistent with the data, but a value of ~70 km/s/Mpc is still possible, as various points on the graph show; it would simply alter a few other cosmological parameters (more dark energy and less dark matter) that might still paint a fully consistent picture.

What if everyone is correct?

There’s an underlying assumption behind the expanding Universe that everyone makes, but that may not necessarily be true: that the energy contents of the Universe — i.e., the number of neutrinos, the number of normal matter particles, the number and mass of dark matter particles, the amount of dark energy, etc. — have remained fundamentally unchanged as the Universe has expanded. That no type of energy has annihilated away, decayed away, and/or transformed into another type of energy over the entire history of the Universe.

But it’s possible that some sort of energy transformation has occurred in the past in a significant way, just as:

• matter gets converted into radiation via nuclear fusion in stars,
• neutrinos behave as radiation early on, when the Universe is hot, and then as matter later on, when the Universe is cold,
• unstable, massive particles decay a way into a mix of less-massive particles and radiation,
• the energy inherent to space, a form of dark energy, decayed away at the end of inflation to produce the hot Big Bang full of matter and radiation,
• and massive particle-antiparticle pairs, which behave as matter, annihilate away into radiation.

All you need is for some form of energy to have changed from when those early, relic signals were created and imprinted some 13.8 billion years ago until we start observing the most distant objects that allow us to trace out the expansion history of the Universe through the distance ladder method several billion years later.

Modern measurement tensions from the distance ladder (red) with early signal data from the CMB and BAO (blue) shown for contrast. It is plausible that the early signal method is correct and there’s a fundamental flaw with the distance ladder; it’s plausible that there’s a small-scale error biasing the early signal method and the distance ladder is correct, or that both groups are right and some form of new physics (shown at top) is the culprit. The idea that there was an early form of dark energy is interesting, but that would imply more dark energy at early times, and that it has (mostly) since decayed away.

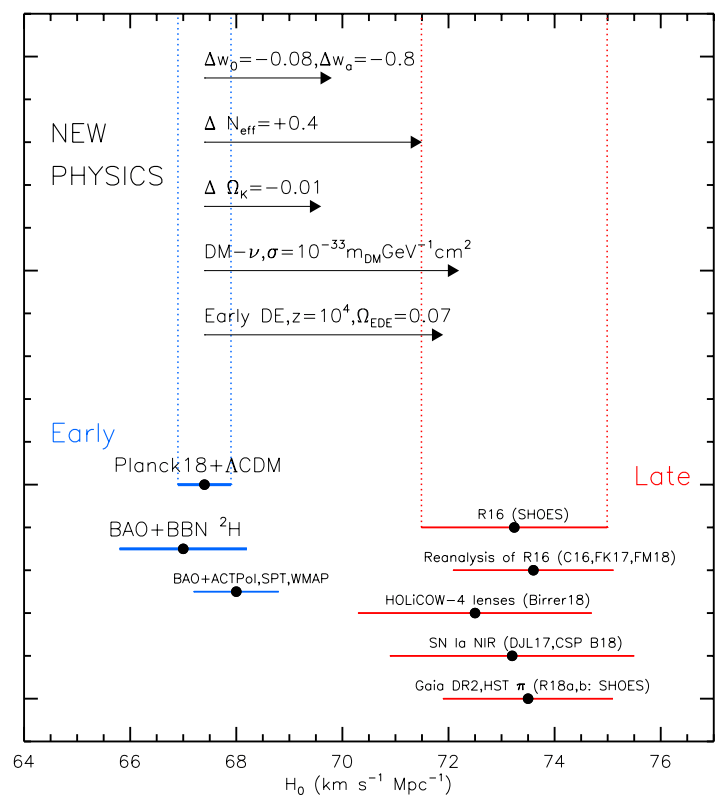
Here is a sampling of possible theoretical solutions that could explain this observed discrepancy, leaving both observational camps “correct” by changing some form of the energy contents of the Universe over time.

• There could have been a form of “early dark energy” that was present during the radiation-dominated stages of the hot Big Bang, making up a few percent of the Universe, that decayed away by the time the Universe forms neutral atoms.
• There could have been a slight change in the curvature of the Universe, from a slightly larger value to a slightly smaller value, making up about 2% of the Universe’s total energy density.
• There could have been a dark matter-neutrino interaction that was important at high energies and temperatures, but that is unimportant at late times.
• There could have been an additional amount of radiation that was present and affected cosmic expansion early on, like some sort of massless “dark photons” that were present.
• Or it’s possible that dark energy hasn’t been a true cosmological constant over our history, but rather has evolved in either magnitude or in its equation-of-state over time.

When you put all the pieces of the puzzle together and you’re still left with a missing piece, the most powerful theoretical step you can take is to figure out, with the minimum number of extra additions, how to complete it by adding one extra component. We’ve already added dark matter and dark energy to the cosmic picture, and we’re only now discovering that maybe that isn’t enough to resolve the issues. With just one more ingredient — and there are many possible incarnations of how it could manifest — the existence of some form of early dark energy could finally bring the Universe into balance. It’s not a sure thing. But in an era where the evidence can no longer be ignored, it’s time to start considering that there may be even more to the Universe than anyone has yet realized.