Ask Ethan: Why don’t neutrons bind together?

- Here in our Universe, all atomic nuclei, stable and unstable, are made up of protons and neutrons, with light nuclei often having equal amounts of both and heavier nuclei having more neutrons than protons.
- The reason for this is the strong nuclear force, whose binding energy makes these “bound states” of protons and neutrons even more stable than their individual, isolated components.
- But there are no stable bound states of “all protons” or “all neutrons,” which doesn’t seem like a necessity. Especially for neutrons, with no net electrical repulsion, why can’t we have “neutronium” in nature?
Here in our Universe, almost every combination of fundamental particles you can imagine will lead to an unstable state. Anything containing a strange, charm, bottom, or top quark will decay in extremely short order, as will anything containing a muon or tau lepton, as well as their antiparticles. In fact, the only quark-containing particles that are stable at all are the proton, and other atomic nuclei (protons and neutrons combined) that contain at least one proton. But if a proton and neutron, when they’re bound together into a deuteron, are more stable together than when they’re free, then why can’t two (or more) neutrons bind together to make a stable, bound state of neutronium?
It’s an idea that dates all the way back to 1926: six full years before the discovery of the neutron. It’s also the question of Scott McGregor, who wants to know:
“I had trouble understanding why a deuterium nucleus is stable, but neutron pairs are not observed. I believe that due to the nuclear force, even a pair of neutrons should be lower energy than separate neutrons… Can you elaborate on this a bit more to explain why neutron pairs don’t exist or are unstable?”
It’s a really fascinating question that reaches deep into the heart of nuclear physics, and carries some surprising insights for us along the way. Let’s dive in and find out!

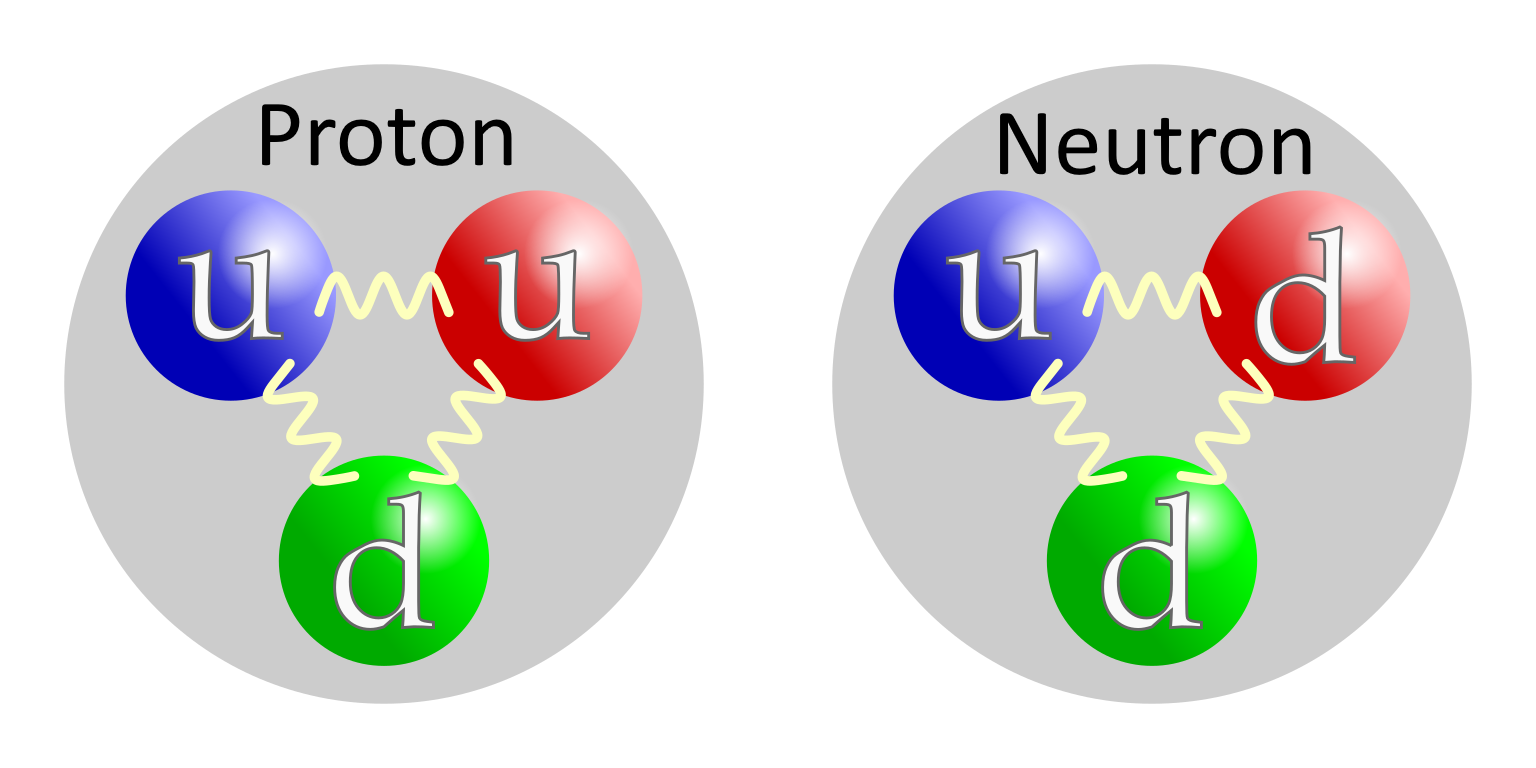
Let’s start with the basics: a free proton and a free neutron, separately. Even though they’re composed of quarks and gluons on the inside — with two up quarks and one down quark for a proton and one up quark and two down quarks for a neutron — it’s the overall properties, rather than the internal properties, of protons and neutrons that are more important for understanding how they bind together. Overall:
- protons have a mass of 938.272 MeV/c², an electric charge of +1, and are fermions, with spins of ±½,
- while neutrons have a mass of 939.565 MeV/c², an electric charge of 0, and are fermions, with spins of ±½.
There are underlying reasons for this that have lots to do with their quark composition, of course. There’s a rule for fermions (which, fundamentally, all quarks are) that doesn’t apply to bosons: you can never have two fermions in the identical quantum state at the same place at the same time. That means the two “up” quarks in a proton must have opposite spins (+½ for one and -½ for the other), and the two “down” quarks in a neutron must have opposite spins, leaving the “leftover” quark (down for the proton and up for the neutron) to determine their overall spin. Because down quarks are slightly more massive than up quarks, and neutrons have two of them compared to the proton’s one, neutrons are slightly more massive than protons.
However, the mass difference between a proton and neutron is only 1.3 MeV/c², even though the mass difference between an up quark and a down quark is closer to ~3 MeV/c², with up quarks having a mass of around 2 MeV/c² and down quarks have a mass of around 5 MeV/c².
Why isn’t there a larger mass difference between protons and neutrons than 1.3 MeV/c², especially if the quarks making up neutrons add up to ~3 MeV/c² more than the quarks making up protons?
Because even inside an atomic nucleus, there’s more than just the spring-like force (the strong nuclear force, mediated by gluons) that binds quarks together. There’s also, even though it’s not the dominant force, the electromagnetic force, which repels like-charged particles and attracts opposite-charged particles. Inside the proton, the two up quarks (of charge +⅔) and one down quark (of charge -⅓) have an overall, net repulsive effect, while inside the neutron, the two down quarks (-⅓) and one up quark (+⅔) have their charges balance out. Even though the quark masses contribute about ~3 MeV/c² to the mass difference between the proton and neutron, the internal electric forces counteract that, and knock that difference back to just ~1.3 MeV/c².
Now, here’s another important piece to the puzzle: if you have a free proton, all by itself, it is perfectly stable. A free proton, as far as we can tell, will never decay into a lighter set of constituent particles, and owing to enormously precise experiments filled with proton-containing molecules (such as water) that have searched extensively for proton decay, we have placed direct lower limits to the lifetime of a proton of ~1034 years, or around ~1040 seconds.
The free neutron, on the other hand, is always unstable, and will decay into a proton, electron, and an electron antineutrino with a mean lifetime of about 880 seconds, or about ~15 minutes. That’s because a proton (938.272 MeV/c²), an electron (0.511 MeV/c²), and an electron antineutrino (~10-8 MeV/c²), even combined, all have less energy inherent to them than a single, free neutron (939.565 MeV/c²) does. With energy, momentum, electric charge, spin, and all other quantum necessities conserved in this decay, the free neutron does not remain stable, but rather results in a common type of radioactive decay known as beta decay.
Free neutrons are unstable; free protons are stable. But when it comes to bound states, we’ve got a different story to tell.
If you take a proton and neutron, they can bind together relatively easily: into a bound state known as a deuteron. Deuterons are also inherently stable; they do not radioactively decay in any way.
There’s a big reason for this: binding energy.
When you bind a proton and neutron together into a deuteron, the act of binding them together leads to the emission of a high-energy photon: a gamma-ray. This is because of the need to conserve energy, as a deuteron, a bound state between a proton and a neutron, “only” has a mass of 1875.613 MeV/c².
Now, you may or may not be a math genius, but you don’t have to be one to test for yourself that the mass of a proton (938.272 MeV/c²) plus the mass of a neutron (939.565 MeV/c²) does not equal the mass of a deuteron (1875.613 MeV/c²). In fact, it’s significantly more: 1877.837 MeV/c². The reason a deuteron has less mass than a free proton and neutron, individually, is because stable, bound entities release energy when they’re formed. It’s why a hydrogen atom has about 13.6 eV/c² less than a free proton and a free electron; it’s why the atoms that are bound together to form the Earth had to release energy in order for our planet to form. The binding energy of a deuteron — about ~2.2 MeV/c² — gets released when they form, and that binding energy is of a great enough amount to keep the neutron inside from ever “decaying” into a proton, electron, and electron antineutrino.
But here’s the funny thing: what do you find when you go and measure the spin of a deuteron?
Given that a deuteron is made of a neutron (with a spin of ±½) and a proton (with a spin of ±½), you might think you could get any of three possible outcomes: +1 (if they’re both +½), 0 (if one is +½ and the other is -½), or -1 (if they’re both -½). But in practice, you will never, ever see a spin 0 deuteron; all of the deuterons you will ever measure are either spin +1 or spin -1.
There’s an incredible reason for that, going all the way back to the strong force: the binding energy between two particles in a nucleus depends on their spins. If the particles have the same spin as one another, the binding energy is stronger, making it easier to form a bound state; if the particles have opposite spins to one another, the binding energy is weaker, making it more difficult to form a bound state.
For the deuteron, made of one proton and one neutron, the particles can both be in the ground (lowest-energy) state and have the same spin inside the atomic nucleus, and that will lead to a stable, bound state. If you put them both in the ground (lowest-energy) state and were to give them opposite spins instead, however, you cannot form a stable bound state; the spin of one (or the other) particle must “flip” in order to make a deuteron.

Now, let’s consider the same problem, but this time, let’s try and make two neutrons bind together into a composite state: one known, theoretically, as a dineutron. Each neutron has a spin of ±½, but this time, instead of having one proton and one neutron, we have two neutrons: two identical particles that happen to be fermions. Unfortunately, as we mentioned earlier, there’s a quantum rule that forbids two identical fermions from occupying the same quantum state: the Pauli exclusion principle. If you insist that your two neutrons both need to be in the lowest-energy (or ground) state, then their spins aren’t allowed to be identical to one another; they must be opposite.
But we just stated, in examining the deuteron, that there’s a problem: the binding energy between two particles depends on their spins, and you get stronger binding for particles with the same spin as one another, and weaker binding for particles with opposite spins. Opposite-spin protons and neutrons can’t form a bound state together, as the binding forces aren’t strong enough. And, although you have to do some pretty heavy-lifting, mathematically, to figure it out, it turns out that the binding energy for two opposite-spin neutrons within the atomic nucleus isn’t strong enough to produce a bound state of two neutrons.
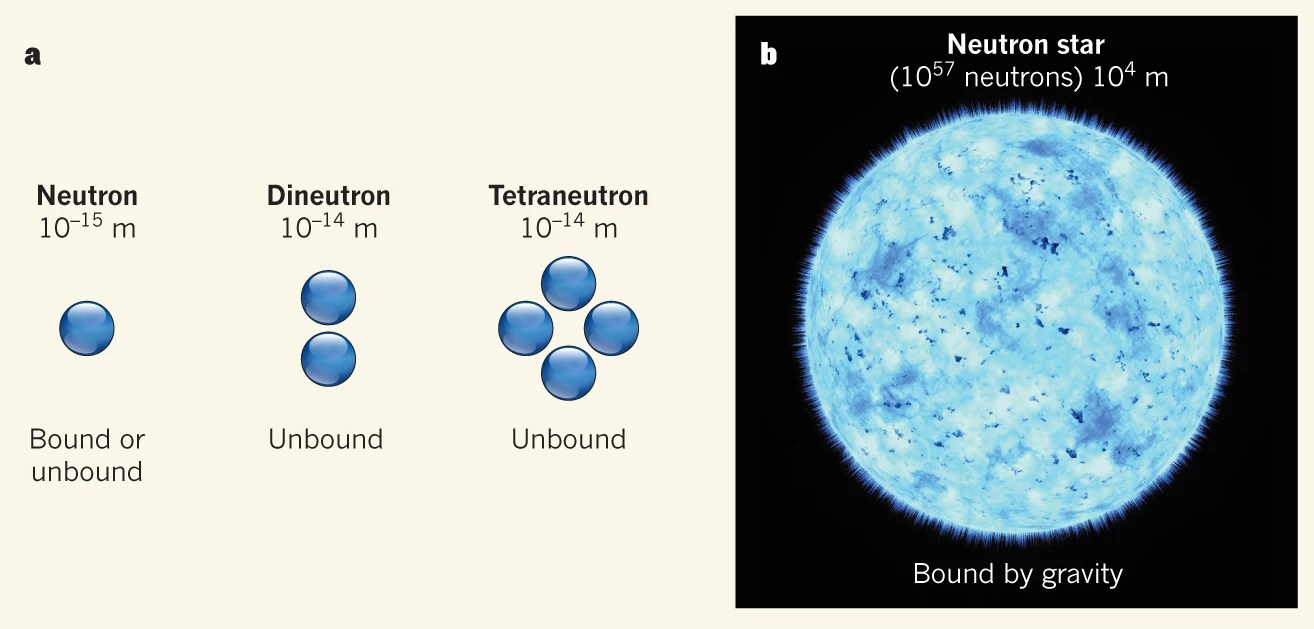
Well before we understood the strong nuclear force, experimentalists started searching for states like the dineutron, with documentation for these searches going all the way back to 1952. As expected, these searches continually came up empty. But in the 2010s, nuclear physicists got a bit of a surprise: when they bombarded certain elements with accelerated deuterons, such as the rare earth element Terbium (Tb), they created a temporary excited state that quickly decayed. One of the decay products that indirect evidence quickly emerged for, perhaps surprisingly, was consistent with an unstable (rapidly decaying) bound state of two neutrons: a dineutron! It looks like, under the right circumstances, the dineutron can exist, even though it’s temporary, rapidly decaying away thereafter.
Unfortunately, the dineutron is incredibly unstable, much more unstable than a single, free neutron. Whereas a neutron can only beta decay into a proton, electron, and electron antineutrino, a dineutron can:
- have one of its neutrons decay into a proton, electron, and electron antineutrino, leading to a much more stable deuteron (plus an electron and an electron antineutrino),
- or simply decay back into two free neutrons, which will then beta decay conventionally after ~15 minutes or so, which is the far more commonly-taken pathway.
As you might suspect, a diproton is even more unstable, because it has all of the instability inherent to the dineutron, plus the electrostatic repulsion between the two protons in the nucleus: both of which are positively charged. And yet, the diproton plays an important role where it counts the most: inside stars.

Inside most stars, including the Sun, the prime pathway by which nuclear fusion takes place is through the proton-proton chain, which starts with bare hydrogen nuclei (protons), and fuses them in a chain reaction to produce first deuterium, then helium-3 or tritium, and then helium-4 from those. However — and this has always seemed remarkable to me — almost every proton-proton interaction that produces a diproton immediately decays back into two free protons. But, importantly, that’s not the only option. A diproton, because it’s more massive than two free protons on their own can either:
- simply decay back into two free protons, which will go back into bouncing around inside a stellar interior,
- or can inverse beta decay: into a deuteron, a positron (an anti-electron), and an electron neutrino.
Because a deuteron has so much negative binding energy, to the tune of ~2.2 MeV/c², a diproton actually has enough mass/energy to decay into a deuteron, plus a positron, plus an electron neutrino, and still have energy left over. Only a teeny, tiny fraction of diprotons created in the Sun, about 1 in every ~1028 or so, will inverse beta decay into a deuteron, and yet this rare, infrequent possibility is the primary way by which the Sun makes deuterium: the first step in the proton-proton chain that powers the Sun and nearly all stars.

However, the only reason that stable, bound states made purely of “all neutrons” or “all protons” can’t exist is because the strong nuclear force isn’t just a little bit stronger. If you turned up the strength of the strong coupling constant — the dimensionless constant that determines the strength of the strong nuclear force — by just 9%, dineutrons would be stable, and you could build up your own “periodic table” of bound neutron states. If you turned it up further, to about 13% more than its present value, then even the diproton and other bound states of solely protons would exist. It’s only, perhaps, a fluke of nature that in our Universe, proton-and-neutron bound states are stable, but neutronium and protonium states aren’t.
In fact, if the strong force were too much stronger, these bound states of “all neutrons” or “all protons” would actually come to dominate the Universe, and there wouldn’t be any hydrogen left in the aftermath of the Big Bang! This was worked out in 2009, and it turns out you only need to turn up the strong force by about 50% higher over its current value to wind up with a Universe with no hydrogen in it at all, and no possibility of forming stars (or humans) as a result.
In our Universe, however, it’s only within the ultra-dense confines of a neutron star’s interior that states of neutronium can exist: where the gravitational binding energy is great enough to contribute significantly to the nuclear binding energy. Beyond that, they simply aren’t stable. In this existence, the strong nuclear force simply isn’t strong enough to make them so.
Send in your Ask Ethan questions to startswithabang at gmail dot com!