Ask Ethan: Why don’t neutron stars decay?

- The neutron, the second-lightest particle made up of three quarks (behind the proton), isn’t stable like the proton is: a typical free neutron decays away after 10-15 minutes.
- However, some configurations of atomic nuclei, containing both protons and neutrons within them, can be stable; their internal neutrons will never decay.
- So how, then, are neutron stars stable? Do they behave like a giant atomic nucleus? And are there ever conditions where neutron stars are unstable? Let’s find out.
One of the most exotic naturally occurring objects in the Universe is the neutron star: achieving some of the highest densities, temperatures, and energies found anywhere outside of a black hole or separate from the Big Bang. Often containing more than a solar mass worth of matter compressed into a sphere just 10-20 kilometers across, neutron stars generate the strongest magnetic fields in the cosmos, and some neutron stars may even contain more exotic states of matter — like a quark-gluon plasma, possibly including not just up-and-down quarks but heavier species as well — toward their innermost cores.
But neutron stars, as far as we can tell, remain stable over very long timescales. Based on observations of millisecond pulsars, the oldest of the known neutron stars, they must persist for at least hundreds of millions of years, and potentially much, much longer. And yet, if you had just a single free neutron in your possession, it would decay after a mean lifetime of about ~15 minutes. This bothers reader Gary Camp, who wants to know:
“If neutrons decay when not in an atom, why does a neutron star not decay? Is it really a giant atom?”
A neutron star is like a giant atomic nucleus in some ways, in the sense that there is an intense amount of binding energy at play. But unlike the heart of an atom, it isn’t the strong nuclear force doing the heavy lifting here, but gravitation. Here’s the science of why.

Free neutrons
One of the more surprising properties of matter is that of the three main constituents of atoms — protons, neutrons, and electrons — only two of them are inherently stable. The electron, the lightest charged particle in the Standard Model, is perfectly stable to the best of our knowledge, as there are no particles it can decay into (i.e., with less rest mass) and still conserve all of the quantum properties (like electric charge) that it possesses.
The proton, although many have conjectured pathways by which it could decay, appears to be truly stable as well, as experiments searching for proton decay have determined that the proton is stable on timescales of at least ~1034 years, or around a septillion times as long as the present age of the Universe. Even though there are lighter charged particles that the proton could decay into — like a positron and a neutral pion, or a positively charged pion and an antineutrino — those decays would violate baryon number, where a baryon is any composite particle made out of three quarks. The proton is the lightest baryon of all, and hence, it makes sense that it’s stable.
But a neutron, the second-lightest baryon known, actually can decay. Specifically, it conserves all the necessary quantum properties one could consider, including:
- baryon number,
- lepton number,
- lepton family number,
- electric charge,
- and both energy and momentum,
by decaying into a proton, an electron, and an electron antineutrino.
It’s worth looking at what happens on the subatomic level to understand, quantitatively, precisely how this decay occurs. Inside of a proton, there are three valence quarks that determine its nature: two up and one down quarks. Inside of a neutron, for comparison, there are still three valence quarks that determine its nature, but this time, it’s one up and two down quarks. As it turns out, the down quark is just a tiny bit heavier than the up quark, and with an electric charge of -⅓ instead of the up quark’s +⅔ charge, explains why the proton’s total charge is +1 while the neutron’s total charge is 0. All told, a neutron, when you measure its mass, is 939.565 MeV/c², which is very slightly larger than the proton’s mass of 938.272 MeV/c².
Inside of a neutron, when it decays, one of its down quarks decays — mediated by a (virtual) W-boson from the weak interactions — into an up quark, an electron, and an electron antineutrino. This can occur because the electron has a mass of only 0.511 MeV/c², and the neutrino’s mass is well below that. With 1.293 MeV of energy to “play” with, the mass/energy gap between a neutron and a proton, there’s plenty of room for a neutron to decay and still obey all of the necessary conservation laws. The measured mean lifetime of the free neutron is just under 15 minutes, or if you prefer half-life, that’s just over 10 minutes.

Neutrons in an atom
However, the story is very different if your neutron isn’t free, but rather is bound together with at least one proton (and potentially other protons and/or neutrons) inside an atomic nucleus. Here’s a fun example.
- If you put a free proton on a scale (or other apparatus) to measure its mass, you find it weighs in at 938.272 MeV/c².
- If you put a free neutron on a scale, it weighs in at 939.565 MeV/c².
- But if you allow a proton and neutron to bind together, forming a deuteron (or the heart of a deuterium nucleus, also known as “heavy hydrogen”), it now weighs in at 1875.612 MeV/c².
This last number should bother you! After all, a deuteron is made out of a proton and a neutron, and if you add up the mass of a proton and a neutron together, you get 1877.837 MeV/c², not 1875.612 MeV/c².
What’s going on here? It’s as though the very act of binding these two composite particles together is somehow reducing their total mass. As it turns out, this is an incredibly important physical phenomenon.
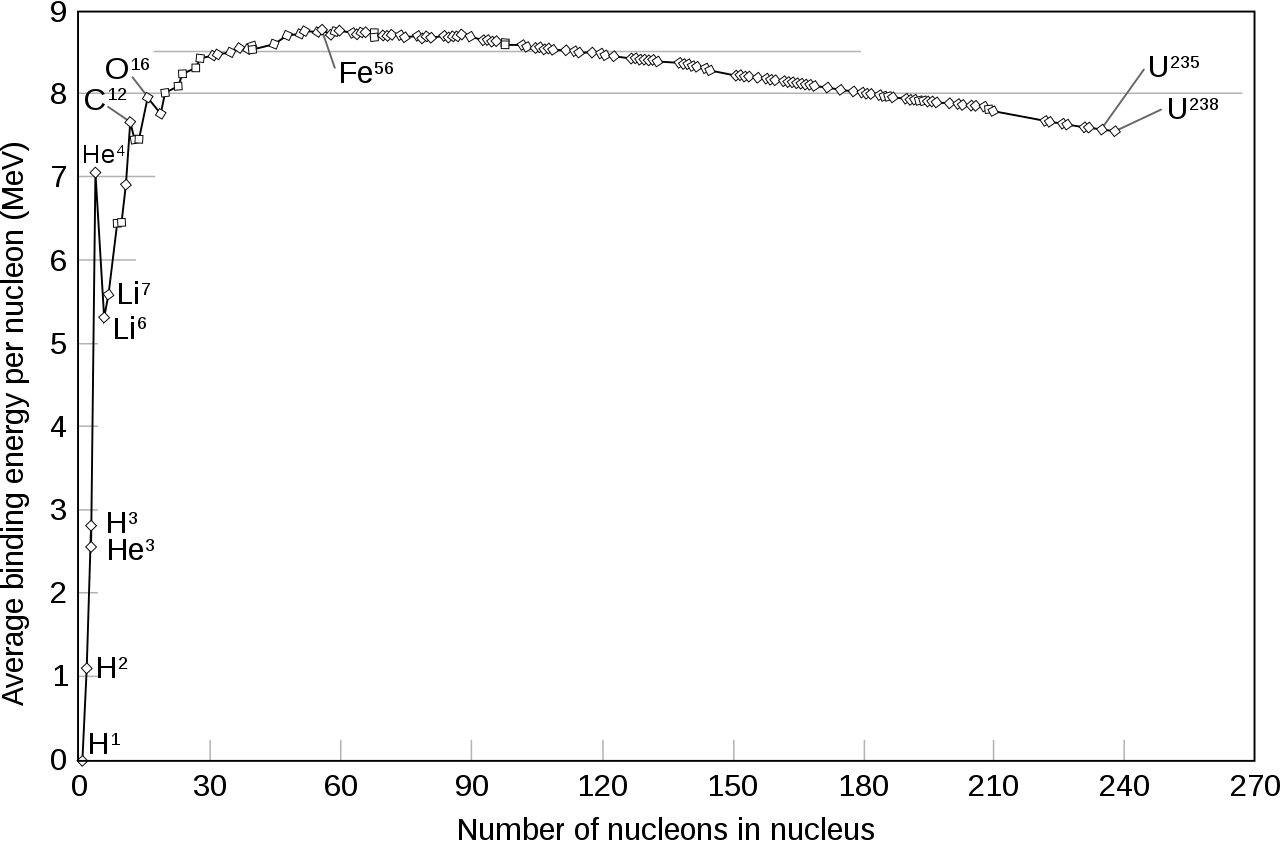
This is the phenomenon, in fact, that makes nuclear fusion possible. It’s only owing to the fact that there are more energetically stable states where protons and neutrons are bound together that allows fusion to take place and release energy: the process powering every star in the Universe. The amount of mass/energy that is lost due to this binding process is known as binding energy, and it occurs within all atomic nuclei that contain two or more nucleons (the generic word for either a proton or neutron).
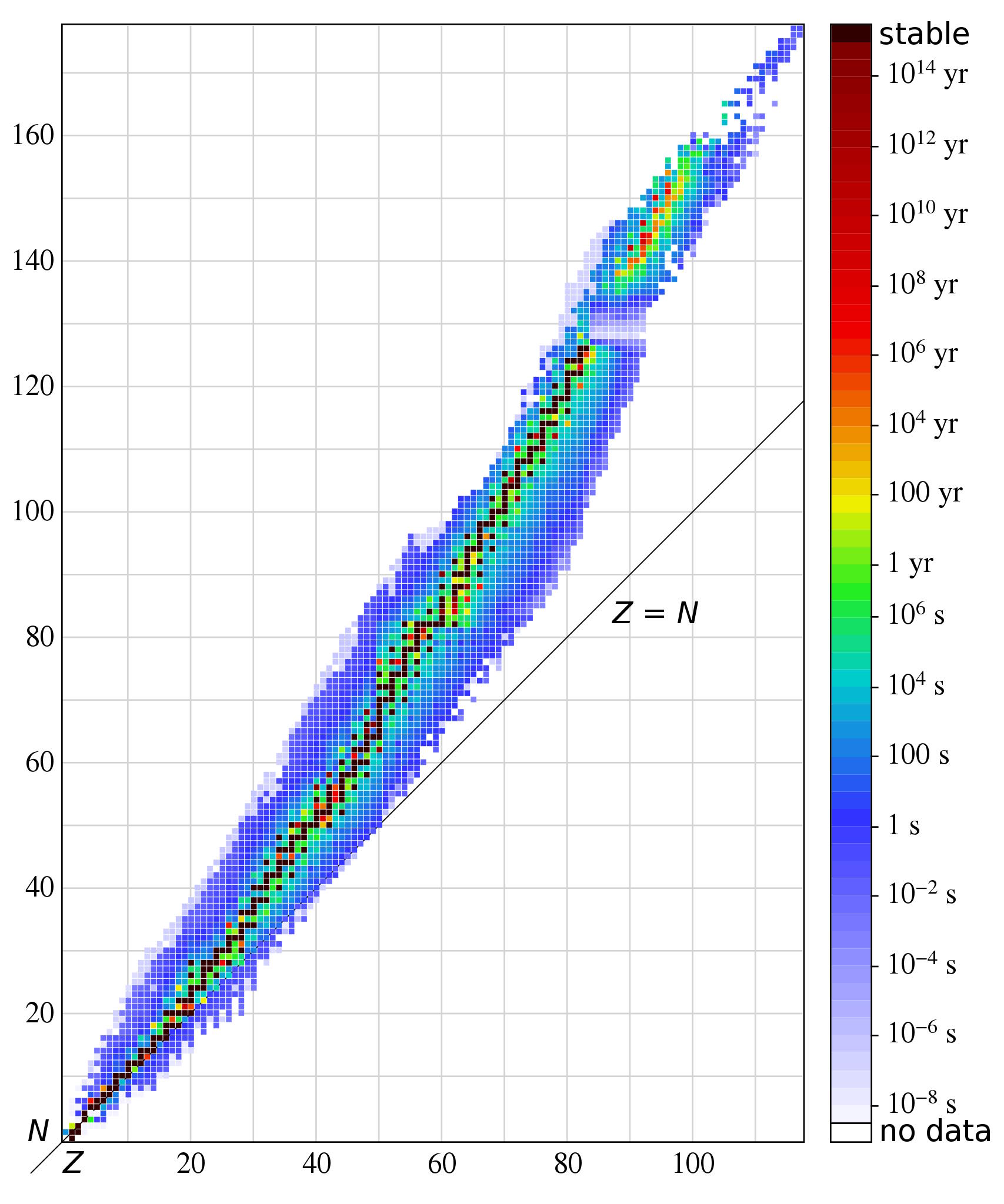
Deuterium, made out of a proton and neutron, has a binding energy of only 2.2 MeV/c², making it relatively fragile. A helium-4 nucleus, made out of two protons and neutrons, has a much greater binding energy: 28 MeV/c², making it much more stable and much more difficult to destroy. Various isotopes of the elements iron and nickel are the most energetically stable combinations of protons and neutrons known to humanity, as shown on the stability diagram of the elements, above and below.
In general, if your binding energy-per-nucleon is large enough, and there aren’t any more stable configurations that your nucleus can easily decay into, it will remain stable. However, if it can transition to make a more stable configuration, it will do that instead; those elements/isotopes are the ones we label as radioactive. As far as we know, experimentally, 251 unique configurations of protons and neutrons are stable so far, but that number should decrease as we measure increasingly rarer and harder-to-detect decays.
Neutrons in a neutron star
For a neutron star, however, it isn’t the strong nuclear force that holds the neutrons together and keeps them “bound” the way they do inside an atomic nucleus. Instead, it’s the gravitational force that’s responsible, which seems counterintuitive, given that gravity, on a fundamental level, is actually the weakest known force of all. However, unlike the strong, weak, and electromagnetic forces, gravity is always a cumulative, long-range force. There are no “opposite” charges out there to the positive (massive) gravitational charge; it’s always attractive. And unlike the nuclear forces, gravitation has an infinite range, not just a short one that falls off rapidly.
In practice, this means that when you accumulate enough mass together — since there’s no practical limit on how much mass you can accumulate in one place — you’re going to have a large amount of binding energy in that system as well, only this time, it will be gravitational binding energy keeping the object together. Gravitational binding energy holds together all of the massive objects in the Universe you’re familiar with: rocky planets, gas giants, brown dwarfs, stars, white dwarfs, and yes, even neutron stars. However, not every “neutron” in a neutron star experiences the same forces acting upon it.
One of the things you must remember about gravitationally bound objects is that there’s an enormous difference in the pressure they experience near their center versus at their surfaces. This is evident even on Earth: the pressure at our surface is one atmosphere, or about 101,000 pascals. However, at Earth’s center, the pressure reaches 364 billion pascals, or about 3.6 million atmospheres!
For a neutron star, the density at its surface — or outer edge of the neutron star’s crust — is relatively small: only ~1 million tonnes per cubic meter. Meanwhile, deep inside, the density reaches nearly one billion times that great near the center, making it denser than even the interior of a uranium nucleus. The center of a neutron star, as far as we know, is the densest place in the Universe except for the singularity at the center of a black hole.
This also results in a tremendous pressure gradient across the interior of a neutron star, which is perhaps a thousand times greater at its core than in its crust. Due to the gravitational effects binding a neutron star together, a neutron star could be as low in mass as about the planet Saturn and still have stable neutrons at its core. (Such a neutron star would be about the size of the Epcot center sphere at Florida’s Disney World.) However, outside of the core, the weaker gravitational binding would cause those more exterior neutrons to decay, setting a lower limit on the mass of a neutron star.

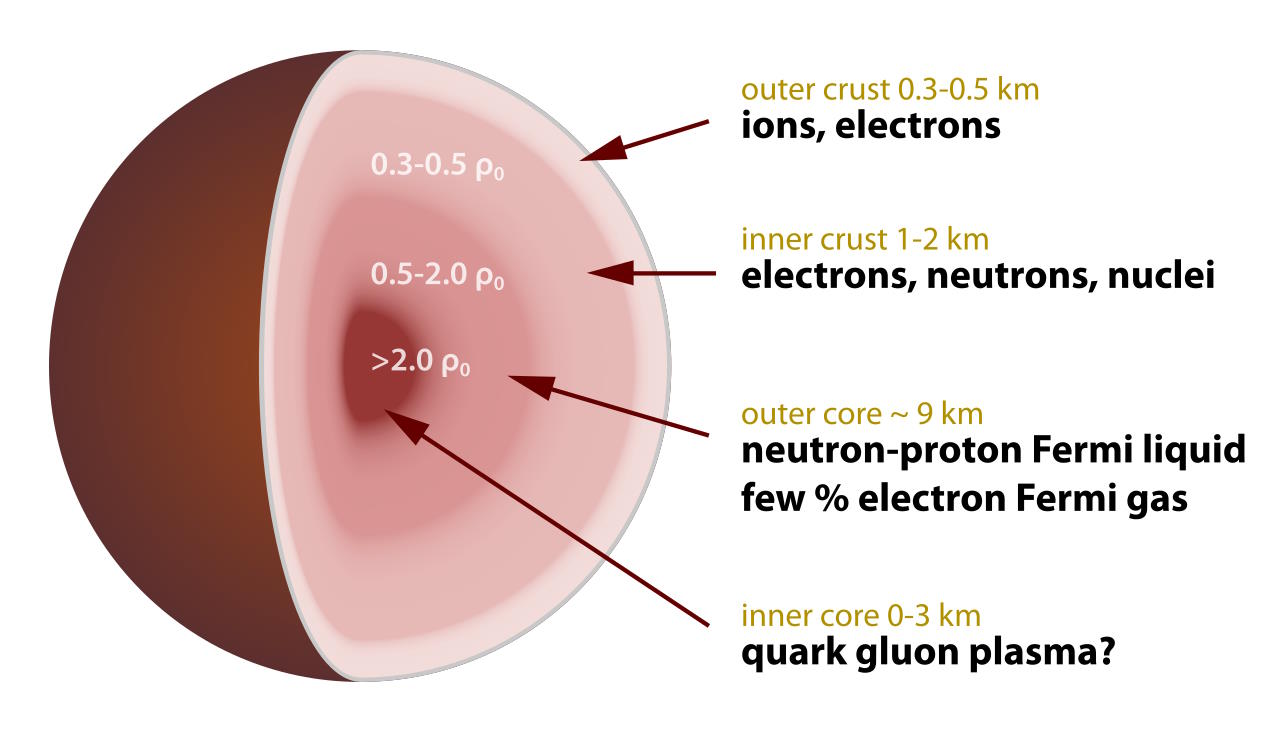
However, real-world neutron stars are far more massive than the planet Saturn: by typically a factor of 1000 or more. These neutron stars have a radius of around 10 kilometers or so, and typically consist of four major regions.
- The innermost core: this region contains super-dense matter under conditions that we cannot replicate in the laboratory or anywhere else. In addition to neutrons, there may be a quark-gluon plasma, perhaps even containing strange quarks, or even what’s known as quark-degenerate matter. Inside, the matter may achieve a superfluid-like state.
- The outer core: comprising most of the volume of a neutron star, this region is practically 100% neutrons, all bound together into much smaller volumes than neutrons typically occupy. They’re joined by occasional proton-and-neutron combinations, bound together in superheavy nuclei. Although these nuclei would be unstable against radioactive decay if they were removed from the neutron star — just as a free neutron would be unstable — the intense gravitational binding energy prevents them from decaying.
- The inner crust: it’s best to think of this as a “transition zone,” where there are loads of neutrons, superheavy elements and isotopes, but also conventional nuclei and free electrons, all at much greater densities, pressure, and in smaller volumes than they’d conventionally be found. There are more neutrons toward the center and more conventional nuclei farther from it, creating a hierarchical set of structures poetically called nuclear pasta: perhaps the strongest form of solid matter in all the Universe.
- The outer crust: only a few hundreds of meters thick, this is mostly composed of “normal” atomic nuclei, crushed into a solid lattice, where electrons freely flow between them. Hard and smooth, the outer crust of a neutron star makes up the roundest objects in the Universe, with surface imperfections measuring smaller than a millimeter: less than 1 part in 10,000,000 away from being a perfect sphere.
The biggest difference between the core and the crust is that, inside the core, individual atomic nuclei cannot be easily separated, in the sense that you cannot easily tell “these neutrons or protons-and-neutrons are bound together in these specific configurations” as they’re all jumbled together. In the core, all the atomic nuclei present “touch” one another, and cannot so easily be separated, either in theory or in practice. In the crust, however, there are many more “void” regions, or simply, spaces between the various atomic nuclei that exist in that volume of space. Individual atomic nuclei can be easily discerned from one another, and it’s clear what each individual bound state is, distinct from one another.
In other words, you perhaps could view the interior of a neutron star — the entire core region or at least the majority of it — as a single atomic nucleus, all bound together, but it’s not the strong nuclear force that causes this binding at all. In this case, it’s the combined effects of:
- the gravitational force of a tremendous amount of this ultra-dense matter,
- and the external pressure (where pressure is a force over an area) pressing down on this matter,
that cause it to behave as though it’s a single, bound entity. The matter here is almost exclusively neutrons, but the average volume of a neutron is significantly smaller than a conventional “free” neutron, compressed down by these tremendous forces acting on them.

So yes: neutrons in a neutron star don’t decay for the same fundamental reason that neutrons in an atomic nucleus don’t decay: because of the binding energy acting on them. However, whereas it’s the strong nuclear force that’s the cause of that binding energy within an atomic nucleus, there’s an even stronger force at play when it comes to the interior of the neutron star: gravity. This manifests itself both in terms of the gravitational force holding the neutron star itself together as well as in terms of the crushing pressure exerted by all of the “exterior” material onto the core of what lies inside the neutron star.
You can’t quite consider the whole neutron star as a single atomic nucleus, however, as the outer portion of the neutron star isn’t “neutrons” at all, but rather a mix of neutrons, exotic and normal nuclei, and electron, all found in various states of extremely dense matter. You can also be certain that, below about the mass of Saturn, there won’t be any stable neutron stars at all, as any “free neutrons” found within them would decay, destroying the object from the outside-in. Wherever you have a free neutron, or a neutron bound into a state with insufficiently large binding energy, its decay is inevitable; the only true question is the duration of time it will take. Neutron stars, however, appear to be stable, and gravitational binding energy is the sole reason why!
Send in your Ask Ethan questions to startswithabang at gmail dot com!