Did physicists get the idea of “fundamental” wrong?

If all you start with are the fundamental building blocks of nature — the elementary particles of the Standard Model and the forces exchanged between them — you can assemble everything in all of existence with nothing more than those raw ingredients. That’s the most common approach to physics: the reductionist approach. Everything is simply the sum of its parts, and these simple building blocks, when combined together in the proper fashion, can come to build up absolutely everything that could ever exist within the Universe, with absolutely no exceptions.

In many ways, it’s difficult to argue with this type of description of reality. Humans are made out of cells, which are composed of molecules, which themselves are made of atoms, which in turn are made of fundamental subatomic particles: electrons, quarks, and gluons. In fact, everything we can directly observe or measure within our reality is made out of the particles of the Standard Model, and the expectation is that someday, science will reveal the fundamental cause behind dark matter and dark energy as well, which thus far are only indirectly observed.

But this reductionist approach might not be the full story, as it omits two key aspects that govern our reality: boundary conditions and top-down formation of structures. Both play an important role in our Universe, and might be essential to our notion of “fundamental” as well.

On the right, the gauge bosons, which mediate the three fundamental quantum forces of our Universe, are illustrated. There is only one photon to mediate the electromagnetic force, there are three bosons mediating the weak force, and eight mediating the strong force. This suggests that the Standard Model is a combination of three groups: U(1), SU(2), and SU(3), whose interactions and particles combine to make up everything known in existence. Despite the success of this picture, many puzzles still remain.

This might come as a surprise to some people, and might sound like a heretical idea on its surface. Clearly, there’s a difference between phenomena that are fundamental — like the motions and interactions of the indivisible, elementary quanta that compose our Universe — and phenomena that are emergent, arising solely from the interactions of large numbers of fundamental particles under a specific set of conditions.

Take a gas, for example. If you look at this gas from the perspective of fundamental particles, you’ll find that every fundamental particle is bound up into an atom or molecule that can be described as having a certain position and momentum at every moment in time: well-defined to the limits set by quantum uncertainty. When you take together all the atoms and molecules that make up a gas, occupying a finite volume of space, you can derive all sorts of thermodynamic properties of that gas, including:

• the heat of the gas,
• the temperature distribution that the particles follow,
• the entropy and enthalpy of the gas,
• as well as macroscopic properties like the pressure of the gas.

Entropy, pressure, and temperature are the derived, emergent quantities associated with the system, and can be derived from the more fundamental properties inherent to the full suite of component particles that compose that physical system.

This simulation shows particles in a gas of a random initial speed/energy distribution colliding with one another, thermalizing, and approaching the Maxwell-Boltzmann distribution. The state of reaching thermal equilibrium is when all parts of the system can exchange energy, collide with, and interact with all other parts of the system freely, and is easy to achieve for a closed, isolated, unchanging system. By contrast, the expanding Universe is wildly out of equilibrium.

But not every one of our familiar, macroscopic laws can be derived from these fundamental particles and their interactions alone. For example, when we look at our modern understanding of electricity, we recognize that it’s fundamentally composed of charged particles in motion through a conductor — such as a wire — where the flow of charge over time determines the quantity that we know of as electric current. Wherever you have a difference in electric potential, or a voltage, the magnitude of whatever that voltage is determines how fast that electric charge flows, with voltage being proportional to current.

On macroscopic scales, the relation that comes out of it is the famous Ohm’s Law: V = IR, where V is voltage, I is current, and R is resistance.

Only, if you try to derive this from fundamental principles, you can’t. You can derive that voltage is proportional to current, but you cannot derive that “the thing that turns your proportionality into an equality” is resistance. You can derive that there’s a property to every material known as resistivity, and you can derive the geometrical relationship between how cross-sectional area and the length of your current-carrying wire affects the current that flows through it, but that still won’t get you to V = IR.

At temperatures greater than the critical temperature of a superconductor, magnetic flux can freely pass through the conductor’s atoms. But below the critical superconducting temperature, all of the magnetic flux gets expelled. This is the essence of the Meissner effect. In a type I superconductor, all of the magnetic flux gets expelled, but in a type II superconductor, the flux can be pinned in certain regions, leading to the phenomenon of magnetic levitation.

In fact, there’s a good reason you can’t derive V = IR from fundamental principles alone: because it’s neither a fundamental nor a universal relation. After all, there’s a famous experimental set of conditions where this relationship breaks down: inside all superconductors.

In most materials, as they heat up, the resistance of the material to current flowing through it increases, which makes some intuitive sense. At higher temperatures, the particles inside a material zip around more quickly, which makes pushing charged particles (such as electrons) through it more difficult. Common materials — such as nickel, copper, platinum, tungsten, and mercury — all have their resistances rise as their temperatures increase, as it becomes more and more difficult at higher temperatures to achieve the same flow of current through a material.

On the flipside, however, cooling a material down often makes it easier for current to flow through it. These same materials, as the temperature lowers and cools them down, exhibit less and less resistance to the flow of current. Only, there’s a specific transition point where, all of a sudden, once a specific temperature threshold (unique to each material) is crossed, where the resistance suddenly drops to zero.

When cooled to low enough temperatures, certain materials will superconduct: the electrical resistance inside them will drop to zero. When exposed to a strong magnetic field, some superconductors will exhibit levitation effects, and with a properly configured external magnetic field, it’s possible to “pin” the superconducting object in place in one or more dimensions, resulting in spectacular applications like quantum levitation. This has not yet been demonstrated for LK-99.

It’s specifically when this occurs that we declare a material has entered a superconducting state. First discovered all the way back in 1911 when mercury was cooled to below 4.2 K, superconductivity still remains only partially explained even today; it cannot be derived or fully explained by fundamental principles alone.

Instead, one needs to apply another set of rules atop the fundamental particles and their interactions: a set of rules known collectively as “boundary conditions.” Simply giving the information about what forces and particles are at play, even if you include all the information you could possibly know about the individual particles themselves, is insufficient to describe how the full system will behave. You also need to know, in addition to what’s going on within a specific volume of space, what’s happening at the boundary that encloses that space, with two very common types of boundary conditions being:

• Dirichlet boundary conditions, which give the value that the solution must attain at the boundary itself,
• or Neumann boundary conditions, which give the value of the derivative of the solution at the boundary.

If you want to create a propagating electromagnetic wave down a wire where the electric and magnetic fields of that propagating wave are always both perpendicular to the wire and perpendicular to one another, you have to tweak the boundary conditions (e.g., set up a coaxial cable for the wave to travel through) in order to get the desired outcome.

This diagram shows a cutaway of the interior of a coaxial cable. With current flowing in one direction down the central, interior cable and the opposite direction down the outer cable, these boundary conditions enable the propagation of an internal “transverse electric-and-magnetic” mode in the space between the conductors. This configuration, known as TEM, can only arise due to the specific boundary conditions present in a coaxial cable-like system. This is for a normal conductor, where all of the charge is transported along the surface.

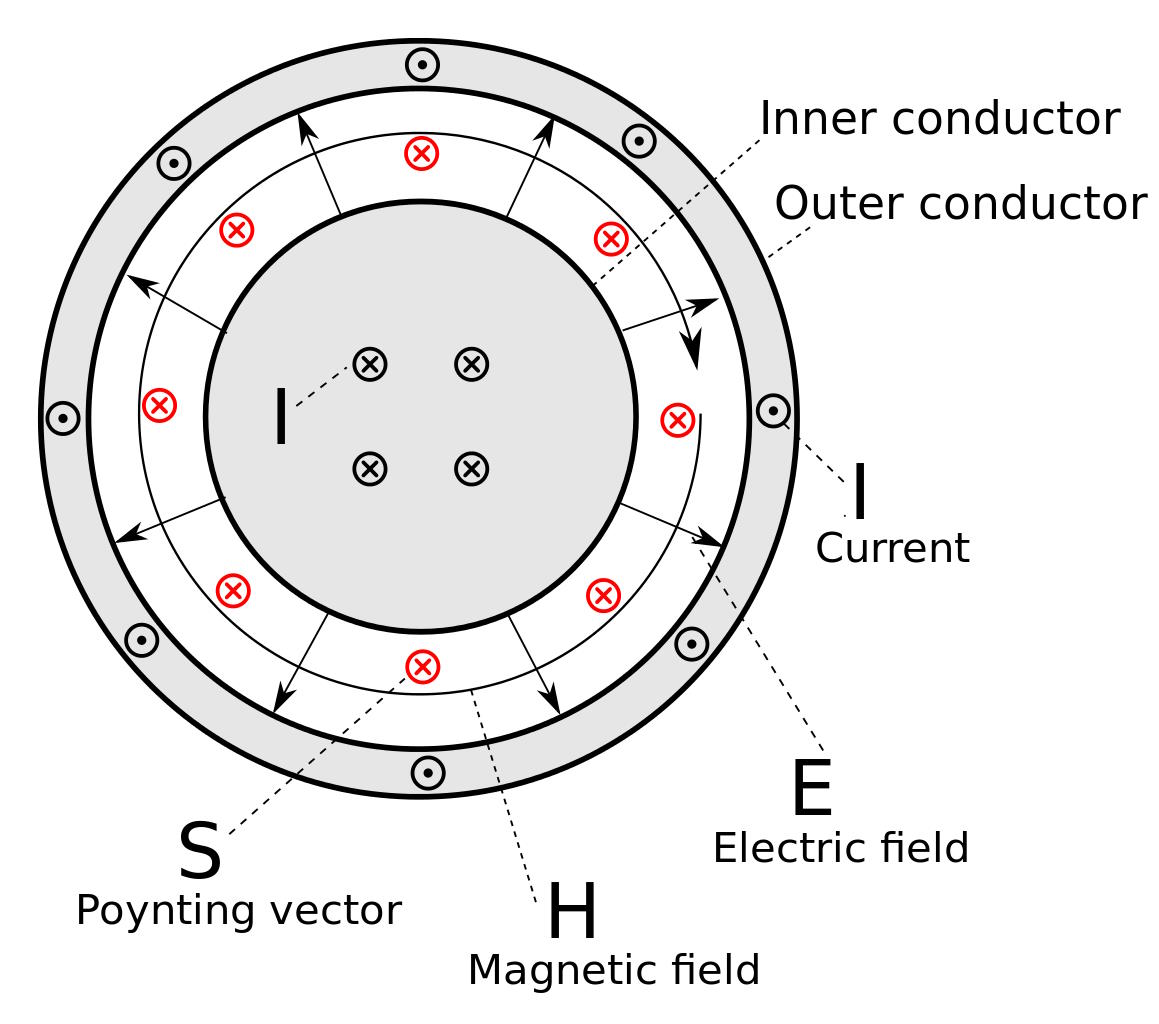
Boundary conditions are of tremendous importance under a wide variety of physical circumstances as well: for plasmas in the Sun, for particle jets around the active black holes at the centers of galaxies, and for the ways that protons and neutrons configure themselves within an atomic nucleus. They’re required if we want to explain why external magnetic and electric fields split the energy levels in atoms. And they’re absolutely going to come into play if you want to learn how the first strings of nucleic acids came to reproduce themselves, as the constraints and inputs from the surrounding environment must be key drivers of those processes.

One of the most striking places where this arises is on the largest cosmic scales of all, where for decades, a debate took place between two competing lines of thought as to how the Universe grew up and formed stars, galaxies, and the grandest cosmic structures of all.

1. The bottom-up approach: which held that small cosmic imperfections, perhaps on the tiny scales of quantum particles, were the first to appear, and then grew, over time, to form stars, then galaxies, then groups and clusters of galaxies, and only later, a great cosmic web.
2. The top-down approach: which held that imperfections on larger cosmic scales, like galactic-or-larger scales, would first form large filaments and pancakes of structure, which would then fragment into galaxy-sized lumps.

This image shows the view of JWST’s NIRCam instrument as it looked at galaxy cluster Abell 2744 and revealed a number of galaxies that are members of a proto-cluster. The red squares show several of the galaxies for which spectroscopic measurements were obtained; the orange circles are photometric galaxy candidates that may yet turn out to be part of this cluster. Small, low-mass galaxies form earlier; larger, evolved galaxies and galaxy clusters only appear at later times.

In a top-down Universe, the largest imperfections are on the largest scales; they begin gravitating first, and as they do, these large imperfections fragment into smaller ones. They’ll give rise to stars and galaxies, sure, but they’ll mostly be bound into larger, cluster-like structures, driven by the gravitational imperfections on large scales. Galaxies that are a part of groups and clusters would have largely been a part of their parent group or cluster since the very beginning, whereas isolated galaxies would only arise in sparser regions: in between the pancake-and-filament regions where structure was densest.

A bottom-up Universe is the opposite, where gravitational imperfections dominate on smaller scales. Star clusters form first, followed later by galaxies, and only thereafter do the galaxies collect together into clusters. The primary way that galaxies form would be as the first-forming star clusters gravitationally grow and accrete matter, drawing adjacent star clusters into them to form galaxies. The formation of larger-scale structure would only occur as small-scale imperfections experience runaway growth, eventually beginning to affect larger and larger cosmic scales.

If the Universe were purely built based on a top-down scenario of structure formation, we’d see large collections of matter fragment into smaller structures like galaxies. If it were purely bottom-up, it would begin by forming small structures whose mutual gravitation brings them together later. Instead, the actual Universe appears to be an amalgam of both, meaning that it’s not described well by either scenario on its own.

In order to answer this question from an observational perspective, cosmologists began attempting to measure what we call “cosmic power,” which describes on what scale(s) the gravitational imperfections that seed the Universe’s structure first appear. If the Universe is entirely top-down, all of the power would be clustered on large cosmic scales, and there would be no power on small cosmic scales. If the Universe is entirely bottom-up, all the cosmic power is clustered on the smallest of cosmic scales, with no power on large scales.

But if there’s at least some power on all manner of cosmic scales, we’d instead need to characterize the Universe’s power spectrum by what we call a spectral index: a parameter that tells us how “tilted” the Universe’s power is, and whether it:

• prefers large scales (if the spectral index is less than 1),
• small scales (if the spectral index is greater than one),
• or whether it’s what we call scale-invariant (where the spectral index equals 1, exactly): with equal amounts of power on all cosmic scales.

If it were this final case, the Universe would’ve been born with power evenly distributed on all scales, and only gravitational dynamics would drive the structure formation of the Universe to get the structures we wind up observing at late times.

The evolution of large-scale structure in the Universe, from an early, uniform state to the clustered Universe we know today. The type and abundance of dark matter would deliver a vastly different Universe if we altered what our Universe possesses. Note the fact that small-scale structure appears early on in all cases, while structure on larger scales does not arise until much later. If this is a good model of reality, the optical light we see should arise from the predicted astrophysical sources within this framework, and nothing more or in excess of that.

When we look back at the earliest galaxies we can see — a set of records that are now being newly set all the time with the advent of JWST — we overwhelmingly see a Universe dominated by smaller, lower-mass, and less evolved galaxies than we see today. The first groups and proto-clusters of galaxies, as well as the first large, evolved galaxies, don’t seem to appear until hundreds of millions years later. And the larger-scale cosmic structures, like massive clusters, galactic filaments, and the great cosmic web, seem to take billions of years to emerge within the Universe.

Does this mean that the Universe really is “bottom-up,” and that we don’t need to examine the birth conditions for the larger scales in order to understand the types of structure that will eventually emerge?

No; that’s not true at all. Remember that, regardless of what types of seeds of structure the Universe begins with, gravitation can only send-and-receive signals at the speed of light. This means that the smaller cosmic scales begin to experience gravitational collapse before the larger scales can even begin to affect one another. When we actually measure the power spectrum of the Universe and recover the scalar spectral index, we measure it to be equal to 0.965, with an uncertainty of less than 1%. It tells us that the Universe was born nearly scale-invariant, but with slightly more (by about 3%) large-scale power than small-scale power, meaning that it’s actually a little bit more top-down than bottom-up.

The large, medium, and small-scale fluctuations from the inflationary period of the early universe determine the hot and cold (underdense and overdense) spots in the Big Bang’s leftover glow. These fluctuations, which get stretched across the Universe in inflation, should be of a slightly different magnitude on small scales versus large ones: a prediction that was observationally borne out at approximately the ~3% level.

In other words, if you want to explain all of the phenomena that we actually observe in the Universe, simply looking at the fundamental particles and the fundamental interactions between them will get you far, but won’t cover it all. A great many phenomena in a great many environments require that we throw in the additional ingredients of conditions — both initially and at the boundaries of your physical system — on much larger scales than the ones where fundamental particles interact. Even with no novel laws or rules, simply starting from the smallest scales and building up from that won’t encapsulate everything that’s already known to occur.

This doesn’t mean, of course, that the Universe is inherently non-reductionist, or that there are some important and fundamental laws of nature that only appear when you look at non-fundamental scales. Although many have made cases along those lines, those are tantamount to “God of the gaps” arguments, with no such rules ever having been found, and no “emergent” phenomena ever coming to be only because some new rule or law of nature has been found on a non-fundamental scale. Nevertheless, we must be cautious against adopting an overly restrictive view of what “fundamental” means. After all, the elementary particles and their interactions might be all that make up our Universe, but if we want to understand how they assemble and what types of phenomena will emerge from that, much more is absolutely necessary.