Physics heresy: Projectiles don’t actually make parabolas
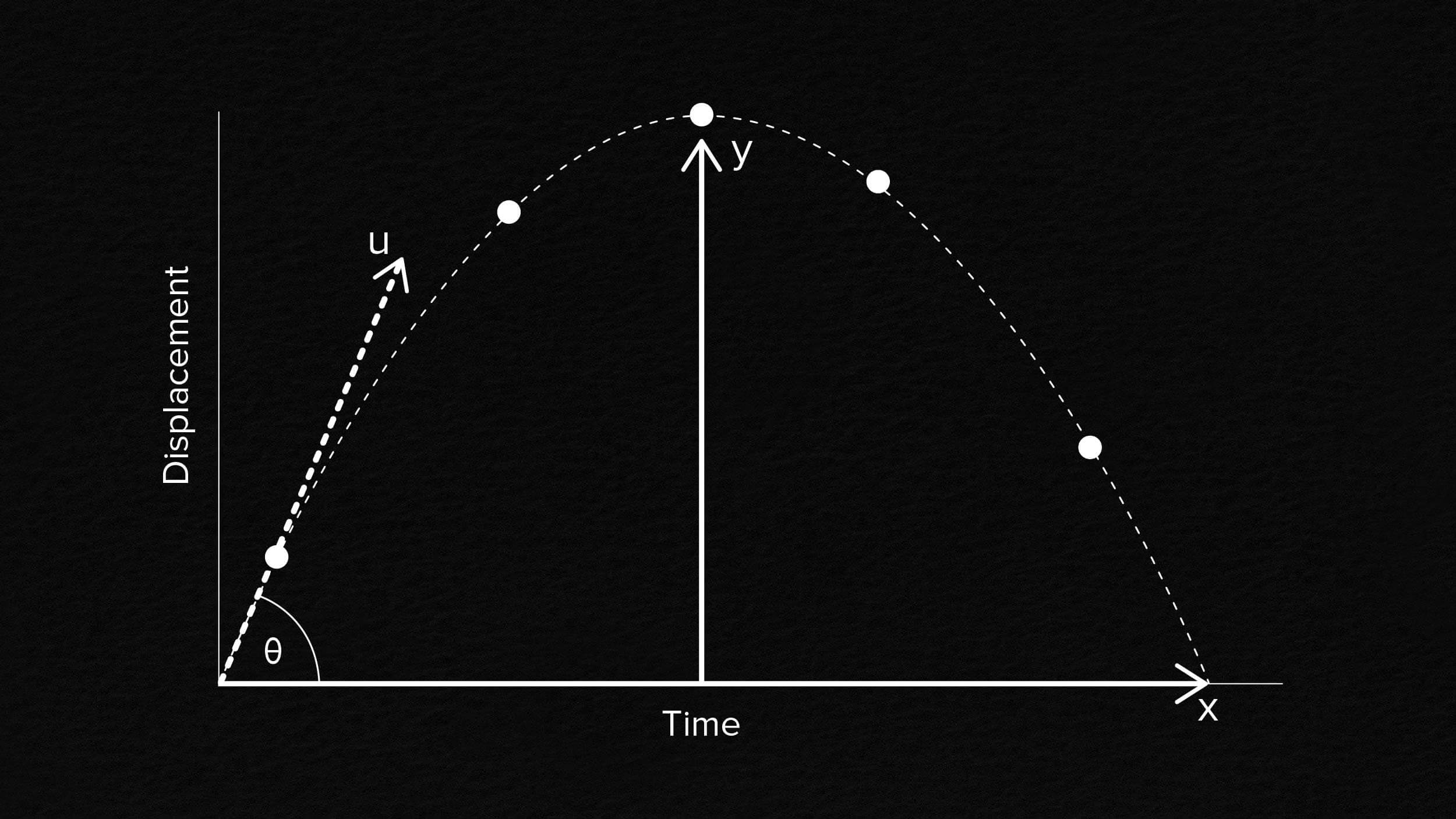
- One of the first classes of problems most students encounter in physics, even in high school, is that of projectile motion: a thrown, shot, or released object subjected to Earth’s gravity.
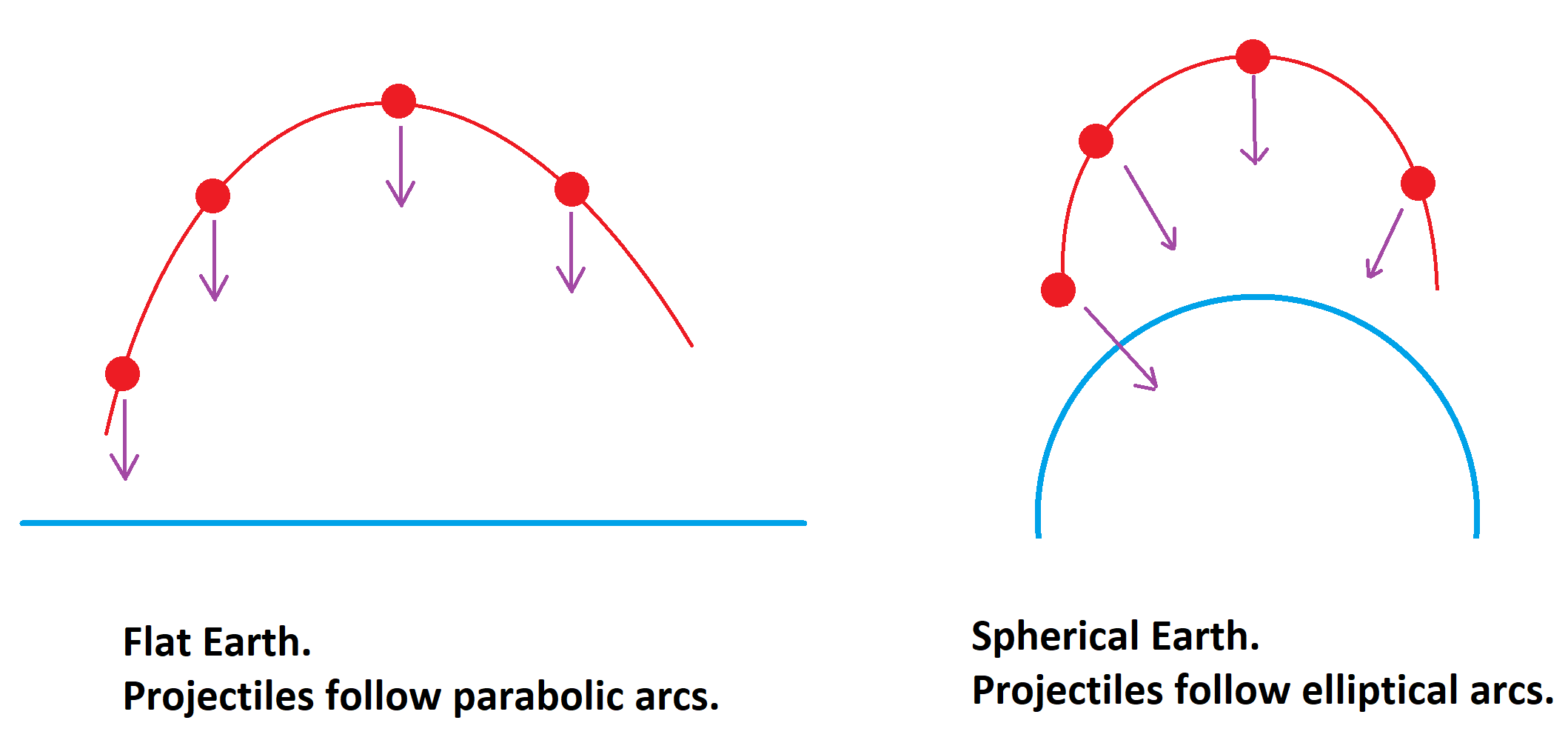
- We learn that the shape this object traces out, regardless of the direction or magnitude of its initial velocity, is a parabola: an excellent approximation for most objects, but not exactly right.
- Even if you neglect air resistance, friction, and all non-gravitational forces, the true shape isn’t parabolic, but is rather a small section of an ellipse. Here’s the science of what actually happens.
As a new school year kicks off across most of the world, a new crop of high school and college students will take physics for the first time, starting off with mechanics and motion. And, as has been the case for hundreds of years, going back to the time of Newton, students will continue to learn the same myth that generations of former students have learned before them: that any object thrown, shot, or fired in the gravitational field of Earth will trace out a parabola before striking the ground. If you neglect external forces like wind, air resistance, or the influence of any other terrestrial objects, this parabolic shape describes how the center-of-mass of your object moves extremely accurately, no matter what it is or what else is at play.
But under the laws of gravity — whether you use Newton’s law of universal gravitation or the rules of Einstein’s general relativity — a parabola is simply an impossible shape for an object that’s gravitationally bound to the Earth to trace out. The math simply forbids it. If we could design a precise enough experiment, we’d measure that projectiles on Earth make tiny deviations from the predicted parabolic path we all derived in class: microscopic on the scale of a human, but still significant. Instead, objects thrown on Earth trace out an elliptical orbit similar to the orbit of the Moon around our planet. Here’s the unexpected reason why.
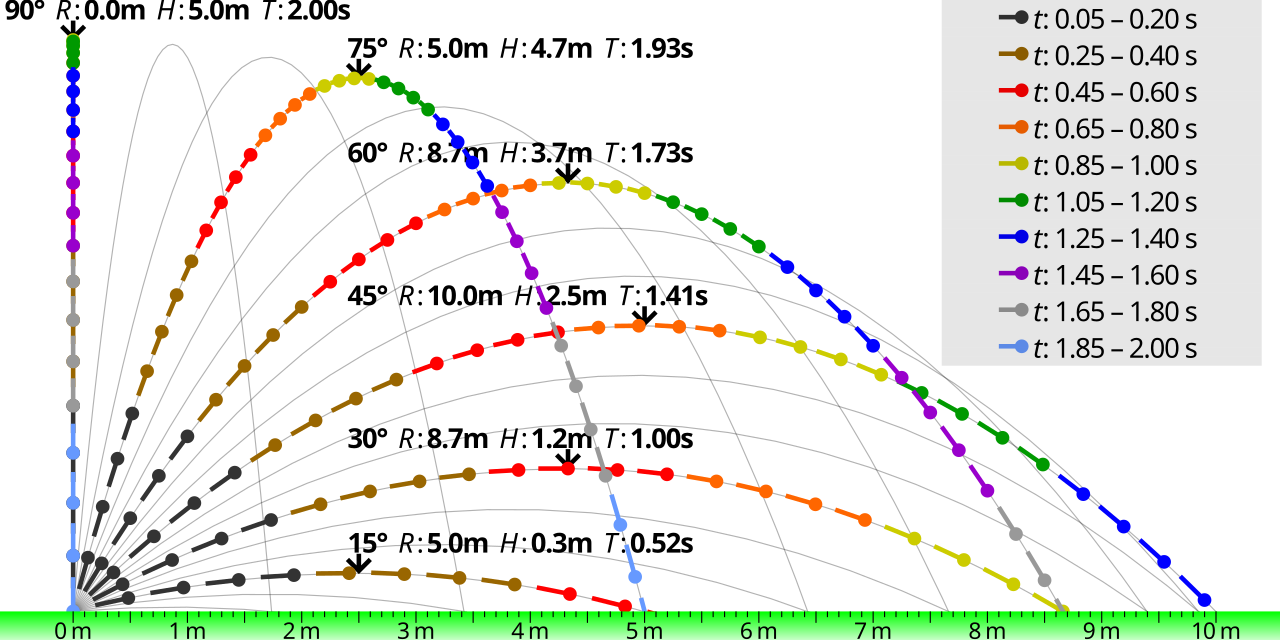
If you wanted to model the gravitational field at Earth’s surface, there are two simplifying assumptions you could make.
- You could assume that the Earth, at least locally in your vicinity, is flat, rather than curved.
- You could assume that the Earth’s gravitational field points straight down relative to your current location, rather than toward the same “point” in space even as your location changes.
Any time you throw and release an object, therefore, the released object enters a situation known as free-fall, regardless of the initial trajectory (including angle and speed) that it possesses.
Further assuming that we neglect all forces other than the force of gravity — no friction, no drag/air resistance, no lift or gliding effects, etc. — it then becomes easy to calculate how the motion of this object will change. In the directions that are parallel to the Earth’s surface (horizontal), the speed of any projectile will remain constant and unchanged. In the directions that are perpendicular to Earth’s surface (vertical), however, your projectile will accelerate downward at 9.8 m/s²: the acceleration due to gravity at Earth’s surface. If you make these assumptions, then the trajectory you calculate will always be a parabola, exactly in line with what’s taught in physics classes around the globe.
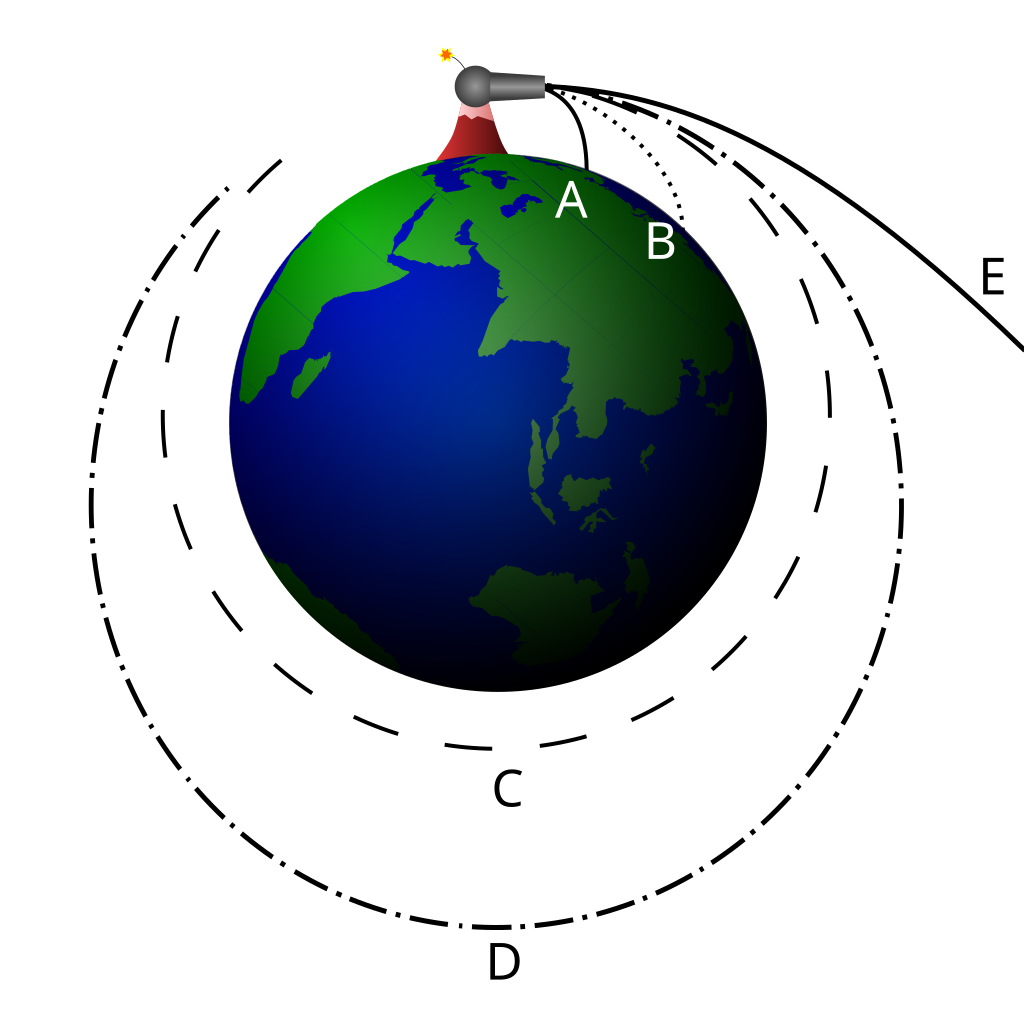
However, of the two assumptions made above, it turns out that neither one of them is exactly true. The Earth may appear flat — so indistinguishable from flat that we cannot detect it over the distances most projectiles cover — but the reality is that the planet, as a whole, takes on a spheroidal shape. Even over distances of just a few meters, the difference between a perfectly flat Earth and a curved Earth comes into play at the 1-part-in-1,000,000 level: a small and subtle level to be sure, but a level that is perceptible with sufficiently precise measuring equipment.
It turns out that this first of our two approximations doesn’t matter so much for the trajectory of an individual projectile, just as local variations in your own backyard render it rather difficult, if not impossible, to measure the curvature of the Earth solely from the terrain present across such a small area.
The second approximation, on the other hand, matters tremendously. From any location along its path, a projectile isn’t truly accelerated “straight down” in the vertical direction, but toward the center of the Earth. A projectile that covers the same modest distance of only a few meters in the horizontal direction will experience a difference in angle between what one might perceive as “straight down” versus “toward the center of the Earth,” and that difference again turns out to come into play at the 1-part-in-1,000,000 level. If we want to get technical about it, this is a consequence of the Earth not being flat, but rather having a spheroidal shape.
For a typical system that you might encounter in nature, something akin to:
- a kicked soccer ball,
- a thrown football,
- or even a home run in baseball,
the deviations from a parabola will show up at a relatively model level: of only tens to perhaps a hundred microns, which is smaller than the length of a single paramecium. But the true trajectory is as fascinating as it is educational, as it was derived by Johannes Kepler more than half a century before Newton came along.
Just like the Moon, any projectile that’s set into motion while gravitationally bound to a point-like mass will trace out an elliptical orbit, with the center of the Earth as one focus of that ellipse. This was Kepler’s first law of planetary motion, and it was the first heliocentric model that correctly described the motion of the planets around the Sun, as well as the moons around their planets and much more. The only difficulty for a projectile on Earth, as opposed to the Moon, is that the Earth can no longer be treated as point-like, as the surface of the Earth itself gets in the way. As a result, humans watching a projectile can only see one tiny portion of the ellipse: the part that rises slightly above the Earth’s surface, reaches the peak of its trajectory (known as apogee in celestial mechanics), and that then falls back toward the Earth’s center, until it strikes Earth’s surface once again.

Each and every time that the surface of the Earth gets in the way of our projectile, however, the problem resets once again. If the projectile bounces at all, it will create an entirely new fragment-of-an-ellipse for its trajectory to follow, which can again be approximated very well by a parabola. Any bouncing ball, whether round like a basketball or shaped differently, like an American football, will see its center of mass trace out a set of parabolas (or near-perfect parabolas) in between each and every bounce. While it’s the gravitational force that’s responsible for the shape while it acts like a projectile, the gravitational force has nothing to do with why the projectile’s trajectory changes every time it strikes the ground.
That happens for a completely different reason that we mostly take for granted: the Earth is made out of the same type of stuff, normal matter, that a typical projectile is made out of. Normal matter, which typically consists of protons, neutrons, and electrons, doesn’t only experience the gravitational force, but nuclear and electromagnetic forces as well. It’s the electromagnetic force that causes the typical interactions we experience between objects that are composed of atoms, enabling elastic and inelastic collisions, and preventing our projectiles from simply slipping through the Earth and tracing out complete ellipses.
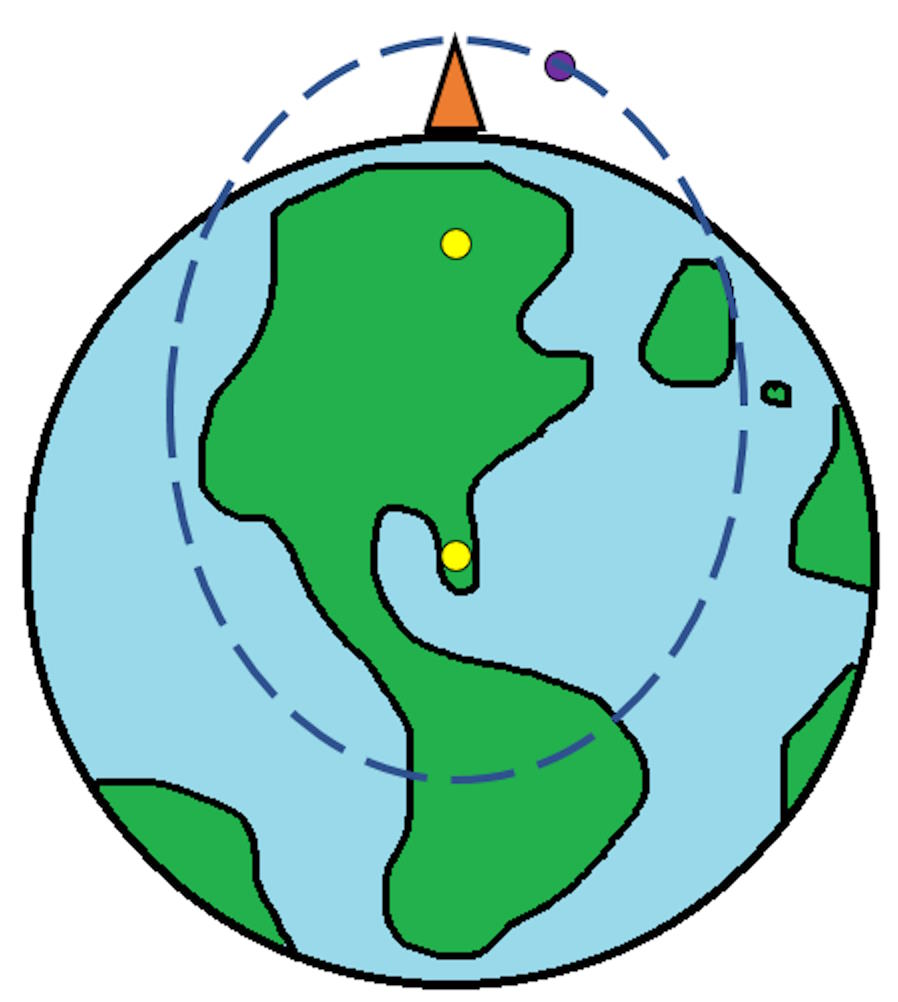
We can get around this problem, however, by imagining that we had something serving as our projectile that possessed no interactions (other than the purely gravitational ones) with normal matter. Perhaps it could be a low-energy neutrino, whose cross-section with matter is negligibly small. Perhaps it could be a particle of dark matter, which may or may not have self-interactions, but which has severe constraints on how much it can interact with normal matter, consistent with no non-gravitational interactions (and a zero cross-section) entirely. In either case, this projectile, once we released it, would only experience the gravitational force, and would pass through the surface and interior of the Earth itself under only the force of gravity.
If you expected that this particle would make a closed ellipse, however, and would return to its original location some ~90 minutes later back above the surface of the Earth from where it was first thrown, you’ve gone and made another approximation that isn’t quite right. When we calculate orbital trajectories, we treat the Earth as a single point: where all of its mass is located directly at its center. When we calculate trajectories of satellites, space stations, and even the Moon, this works just fine. But for a particle that passes through Earth’s surface, that approximation is no good any longer. The Earth, once you go into its interior, turns out to be an extremely complex entity.
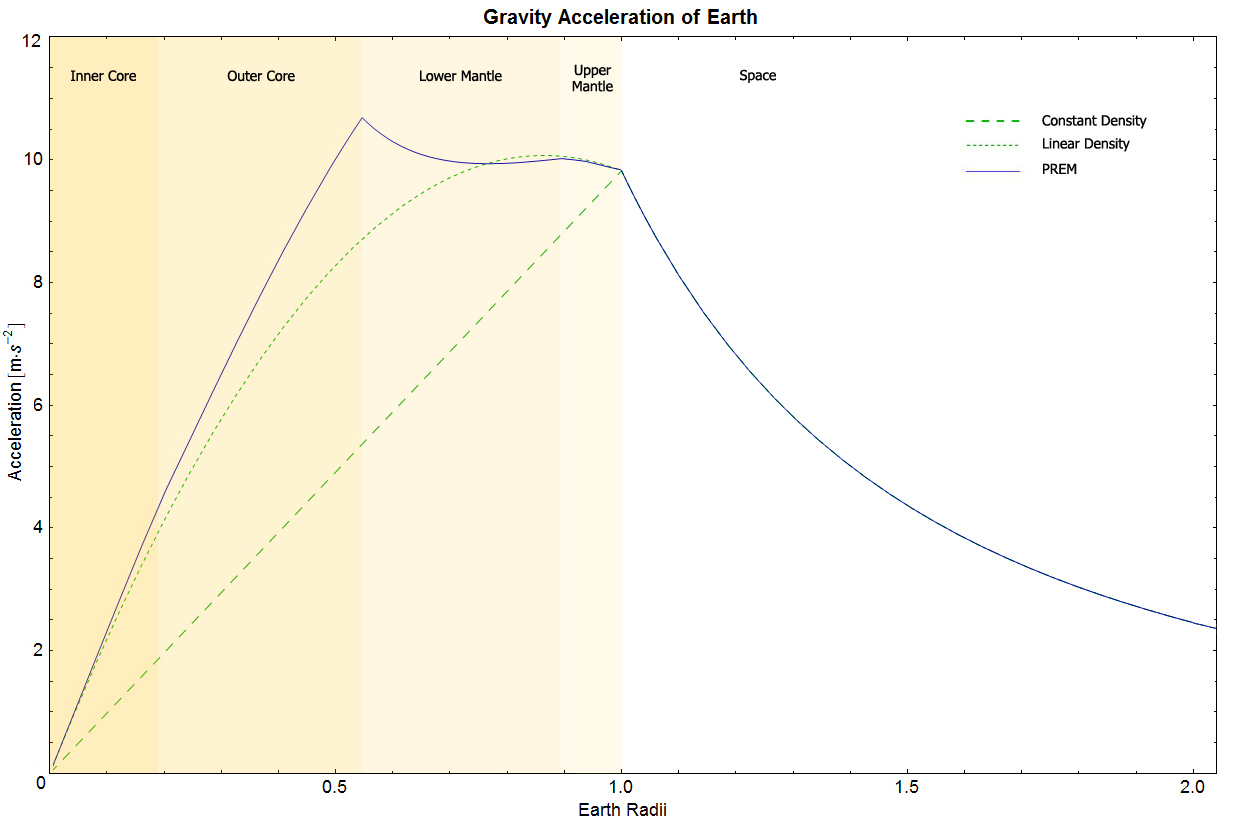
From a gravitational point of view, we have been treating the Earth identically to how we’d treat a “point mass” that was equal to the mass of the entire Earth, but whose location was given by the center (or, more technically, the center-of-mass) of the Earth itself. As long as you’re located on the outside of a mass that’s shaped like a sphere (or spheroid), all of that mass will functionally attract you, under the influence of gravity, toward the center of the object. However, if you’re located within that mass, then it turns out that all the parts of that mass that lie exterior, or farther “outside” of your present location than you are, will have gravitational effects that cancel out, and it will only be the innermore parts of that mass that gravitationally attract you.
In other words, you, an object subjected to the gravitational force of a planet like the Earth, can only feel the gravitational effect of the portion of the Earth that lies interior to you, assuming that everything external to your position is spherically symmetric. In electromagnetism, this is a proven consequence of Gauss’s law; in gravitational physics, it was first proven by Newton for his law of universal gravitation, and was shown to be true even in the context of general relativity as a consequence of (the related) Birkhoff’s theorem. From a practical perspective, this means that once you start falling through the Earth, you experience smaller and smaller amounts of the total internal mass’s gravitational pull.
While there would be no difference between your true trajectory and an idealized ellipse while you, acting as a projectile, were completely exterior to the surface of the Earth, the actual shape of your trajectory would begin to change significantly as you fell through the Earth. It would become:
- longer along the vertical (central) axis,
- less thin-and-compressed as you approached the center of the Earth,
- and would see you moving at a slower velocity than the simple Keplerian prediction as you got closer and closer to Earth’s center,
- followed by a reversal of those phenomena as you approached the far side of the Earth,
- where there’s a chance you’d even briefly emerge out of the other side before “falling” back down to complete the orbit as you re-emerged back at your original location.
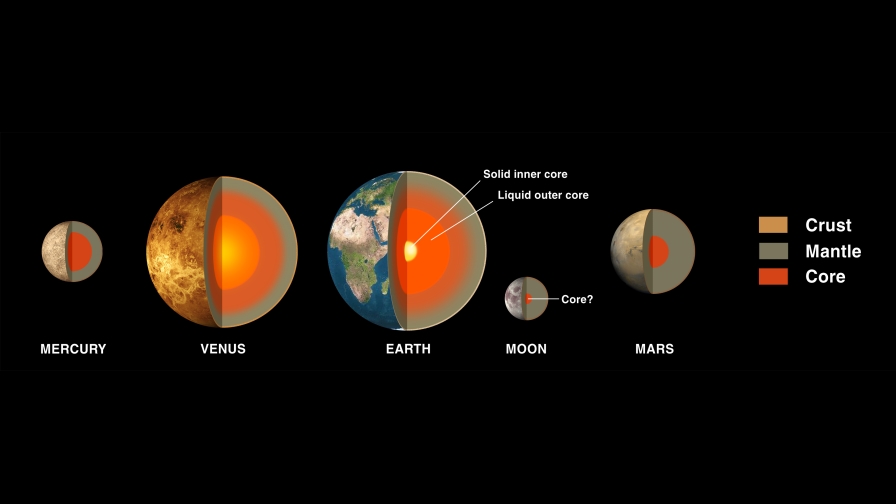
As you passed through the interfaces between various layers, including the mantle-core boundary and the outer-inner core boundary, you’d notice that there were not only smooth changes in your trajectory, but a few discontinuous “kinks” in the shape you traced out, corresponding to the various layers (of varying densities) in the Earth’s interior.
You shouldn’t quite re-emerge out of the Earth’s opposite side, but you would indeed fall past Earth’s center by a large amount, turning around in the mantle or even the crust, dependent on some subtle effects that aren’t so easy to calculate. Not only are the varying densities at different depths not completely known, but the rotational speeds of the varying layers interior to Earth have some uncertainties in them. If you consider even a single mass passing through the Earth, depending on the exact path it takes, dynamical friction, or the forces between individual particles, begins to play a role as well.

When a particle passes by other massive particles, it gravitationally attracts them. If a particle speeds past all of the other ones, it will deflect their trajectories toward where it just passed through, which has the net effect of slowing the motion of the original particle. Depending on which way the original projectile was oriented with respect to Earth’s rotation and internal motions, this can affect the trajectory of whatever particle passes through the Earth by a non-negligible amount.
Over the timespan of a single orbit, which still takes approximately 85–90 minutes or so, this can have a large enough effect so that the projectile doesn’t return to its original starting point. If we combine the effects of:
- the gravitation of an elliptical orbit due to a point mass,
- Birkhoff’s theorem for masses distributed throughout space,
- the varying density, composition, and (possibly) rotation rates of the Earth’s layers,
- and fold in the effects of dynamical friction,
a projectile won’t make a closed ellipse, but will instead return to a point offset by its starting point by up to as much as ~10 meters. Over sufficiently long periods of time and sufficiently large distances, even a one part-in-a-million effect (remember, Earth’s diameter is more than 12,000 kilometers!) can be remarkably substantial.
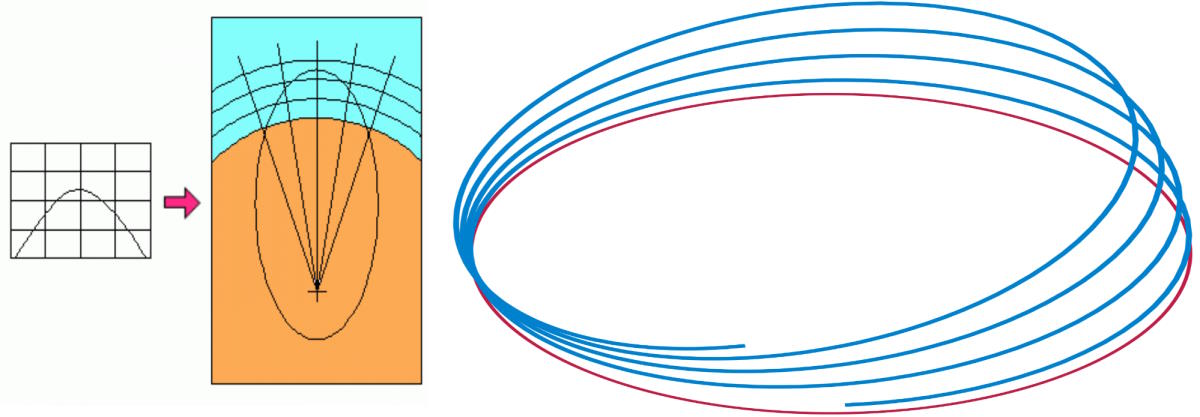
For most practical applications, particularly when a projectile is in flight only for a few seconds above the surface of the Earth, it doesn’t hurt your accuracy to any measurable precision to treat projectiles as simply having a parabolic trajectory. However, if you either:
- care about achieving micron-or-better precision,
- are dealing with a large structure (like a suspension bridge) that spans 100 meters or more,
- or are going to have a projectile that remains in motion for ten seconds or longer (in which case, the effects of air resistance will need to be accounted for as well),
you should no longer treat the Earth’s gravitational field as a constant. Everything is accelerated by the gravity of Earth, but not truly “downward” in any pure, absolute sense. Instead, the gravitational acceleration points toward the center of the Earth, enabling a projectile’s true trajectory — an ellipse — to be revealed.
Studying the various effects that are at play, both external to the Earth as well as within our planet’s interior, can also teach us when and under what circumstances it’s important to make these considerations. For most applications, air resistance is a far larger concern than any effects like the various layers of Earth’s interior or dynamical friction, and treating Earth’s gravitational field as a constant is totally justified. But for some classes of problems, these subtle differences really do matter. We are free to make whatever approximations we choose, but when our accuracy suffers beyond an acceptable threshold, that’s when it becomes critically important to recognize the full suite of what’s truly at play.